一种基于体积力螺旋桨模型的自航计算方法
2015-04-25傅慧萍ThadMICHAELPabloCARRICA上海交通大学船舶海洋与建筑工程学院上海0040IIHRUniversityofIowaIA54USA
傅慧萍,Thad J.MICHAEL,Pablo M.CARRICA(上海交通大学 船舶海洋与建筑工程学院,上海0040; IIHR,University of Iowa,IA 54,USA)
一种基于体积力螺旋桨模型的自航计算方法
傅慧萍1,Thad J.MICHAEL2,Pablo M.CARRICA2
(1上海交通大学 船舶海洋与建筑工程学院,上海200240;2 IIHR,University of Iowa,IA 52242,USA)
文章以集装箱船模型KCS(KRISO Container Ship)为研究对象,基于通用CFD软件FLUENT 12.0.16,采用螺旋桨体积力模型,实现了模型尺度下实船自航点的全粘带自由面计算。该文的计算包括静水拖航计算、自航计算,以及扭矩对自航计算结果的影响分析。通过与试验值的分析比较,验证了该方法的有效性。由于采用了完全结构化的六面体网格,带对称面的计算域单元数仅为33万。研究结果还表明:考虑扭矩的全流场计算对于改善流动细节,获得更精确的计算结果是有利的,但计算量有所增加。
集装箱船模;自航计算;体积力螺旋桨
0 引 言
计算流体力学(CFD)与计算机技术的并行高速发展,使对一切复杂的流动现象在模型尺度下进行直接数值模拟成为可能。而在此之前,由于计算机硬件条件的限制,计算流体力学的研究目标是把一切与流动相关的机理,进行模型化。以船舶水动力计算为例,早期对船桨相互作用的计算,通常是将船体域和桨域分开计算,分别以RANS方程和升力面理论作为基本计算方法,船桨相互作用以迭代的方式进行[1]。随着CFD技术的长足发展,及与之同步发展的计算机技术,基于雷诺平均的考虑粘性的复杂物体绕流场的数值模拟基本得到解决。目前正在朝高雷诺数及湍流直接模拟方向发展。而船舶水动力计算发展到现在,也已经从最初的不带自由面的船桨整体计算[2],发展到可以直接进行模型尺度下的船桨整体计算,并计及粘性、自由面[3]。可以预见,借助于超级计算机系统,借助于高效的计算机并行处理技术,不久的将来实船尺度的船桨舵整体计算将成为可能。
但由于上述这些计算都是基于离散数值方法,为了实现网格划分的鲁棒性和为了适应复杂外形的网格划分,非结构化四面体网格或结构化多块重叠网格是比较好的选择,但代价是网格数巨大。尽管可以采用超级计算系统进行并行计算,但仍然需要耗费相当长的计算时间。尤其对于自航计算,由于需要模拟实际自航试验进行多次计算,计算量更是巨大。鉴于此,发展基于小而精巧网格的,适当模化而高效的计算方法是必要的。
KCS为集装箱船模型,是计算船舶流体力学的标模之一[4-5]。文献[6]中对KCS进行了两种混合网格的计算比较,其中效果比较好的一套网格单元数已经达到350万。如果再加上离散化的桨,网格数将逾千万。采用如此庞大的网格进行自航计算,将是极其耗时的。本文将采用网格生成软件Gridgen 15.11生成完全结构化的六面体网格,并基于通用CFD软件平台FLUENT 12.0.16的二次开发,采用体积力螺旋桨模型,实现模型尺度下实船自航点的计算。并通过计算结果与试验值的广泛比较,验证该方法的有效性。
1 几何与计算条件
图1所示为计算对象KCS,其特征尺度和计算条件为:雷诺数Re=1.4×107,傅汝德数Fr=0.26,垂线间长Lpp=7.278 6 m,设计水深D=0.342 m,湿表面积SW=9.437 9 m2,速度U0=2.196 m/s。计算中采用坐标系Oxyz:坐标原点位于船中纵剖面与设计水线面的交线上、艏柱处;x轴沿该交线,指向艉;y轴位于设计水线面上指向右舷;z轴垂直向上。
2 网格
网格划分的最小尺度为物面边界层Δyp,按文献[7]中的公式进行估算。边界层计算要求当地雷诺数y+=30~500。本文按y+≈60的设计条件,取Δyp=0.001 m。船行波波长λ按文献[8]中的公式估算:按速度U0=2.196 m/s,可得λ≈3.09 m。对靠近船体的波系,船身沿船长方向划分100个网格结点是足够的。水线面上下的网格要求正交,一个波高内划分不少于20层。由于波高H≈λ/20=0.154 5 m,ΔH≈0.007 m,实际按0.005 m取。本文基于网格生成软件Gridgen15.11,进行KCS网格划分。由于流动的对称性(关于中纵剖面,当不考虑螺旋桨扭矩时),取一半的船体进行网格划分,最后生成的网格共包含33万六面体单元。当考虑扭矩时,需要对全流场进行计算,则只需将网格关于对称面进行镜像拷贝即可。图2所示为船艏处对称面、物面及空气压力出口网格。
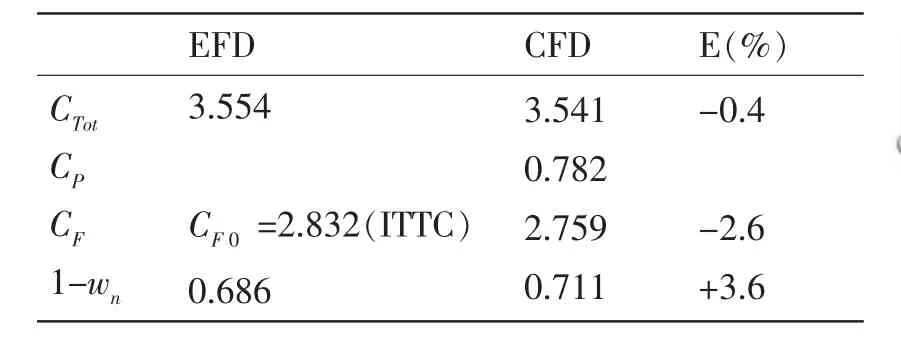
表1 阻力系数(×10-3)及伴流分数预报Tab.1 Prediction of resistance coefficients and nominal wake coefficient

图1 KCS几何形状及船体表面水线Fig.1 KCS geometry and free surface on the hull
3 自航计算方法
实船自航点的计算方法部分来自ITTC(2002)上提出的方法,不同的是体积力模型的使用。本节将在给定摩擦力修正的前提下,通过等推力法得到螺旋桨转速n,推力系数KT等自航因子,并最终得到推进效率η。
3.1 拖航计算
为得到自航因子,需要对给定速度下的拖航状态进行计算。表1给出了船体阻力系数各分量与标称伴流分数及其计算误差。结果表明摩擦阻力CF和总阻力CTot的CFD预报误差分别为-2.6%和-0.4%。伴流分数的预报误差为+3.6%。图3给出了桨盘面下游 (x/Lpp=0.982 5)截面上的轴向速度等值线及横向速度矢量;图4给出了船体表面波形,均与试验吻合得很好。

图2 船艏处网格Fig.2 Mesh at bow
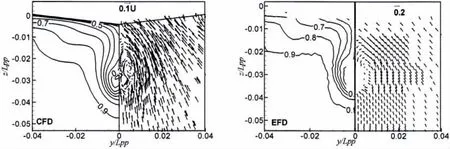
图3 桨盘面下游(x/Lpp=0.982 5)截面上的轴向速度等值线及横向速度矢量Fig.3 Axial velocity contours and cross flow vectors on the propeller plane at x/Lpp=0.982 5
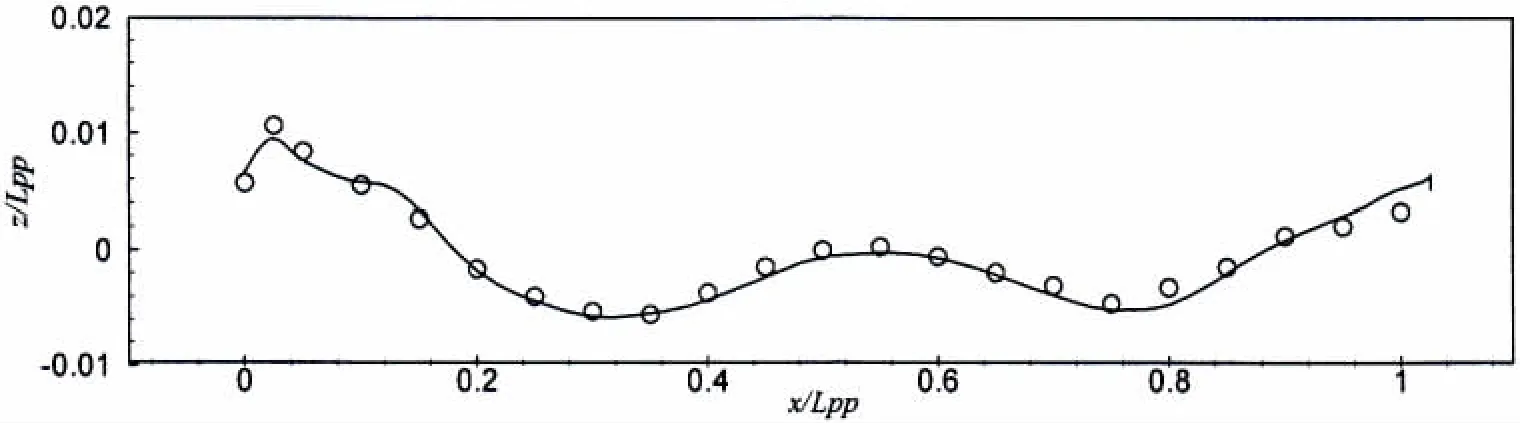
图4 船体表面波形Fig.4 Wave profile on the hull
3.2 自航计算
在体积力分布方法中,螺旋桨的影响通过在动量方程的源项中添加体积力项来计及。这里体积力分布不是作为边界条件,而是作为一个离散的力域嵌入到流场中,从而模拟螺旋桨的作用。本文采用Hough和Ordway载荷分布[9],即假设推力与扭矩沿径向的分布与其引起的环流相似,而后者假设与r*成正比,这里,=(Y - Yh)/(1- Yh),Yh=Rh/Rp(Rp和Rh分别为螺旋桨半径和桨毂半径)。利用这些假设,可以得到下列推力和扭矩(单位体积力)公式:


3.2.1 不考虑扭矩
本节的自航计算根据试验步骤在实船自航点上进行。因此,螺旋桨转速n将被调节,在考虑施加拖曳力的情形下以达到来流方向上力的平衡。此处拖曳力即为表面摩擦力校正(SFC),即有

其中:T为计算得到的推力,RT,SP为自航总阻力,SFC采用试验值30.25 N。令SFC=30.25 N,KT=0.17,n=9.5 rps,进行基于体积力螺旋桨模型的自航计算,得到总阻力RT,SP。并用下式计算推力:

得到推力余量:

如果Te>0,尝试较低的转速,或者相反。由此得到符号相反的两个推力余量。然后进行线性插值,得到推力余量为0对应的转速n=9.308 rps,并最终确定自航推力T=57.534 N(如图5所示)。重新运行此转速下的船桨整体计算,得到RT,SP,以及桨盘面上轴向速度平方的面积平均值=3.876 m2/s2。运用前面拖航计算得到的阻力RT,Tow,即可得到推力减额分数1-t=1-注意:由于KT=0.17是假设的,而n也是在这一给定条件下得到的转速值,因此这一步仅仅是得到确定的推力值。n和KT的确切值还需要在得到进速系数后进一步确定。为了求得在KT=0.17,n=9.308 rps情况下的进速Va,生成一套螺旋桨敞水计算网格。桨轴从速度入口一直延伸到压力出口,螺旋桨依然用体积力模型替代。改变入口速度(从Va=0.8U开始,依次减小),每次至迭代计算收敛后,对桨盘面上的轴向速度平方进行面积平均。然后进行线性插值,得到自航条件下=3.876 m2/s2对应的进速Va(如图6所示)。也就是同样的体积力分布(即相同的KT)下,通过调整Va使敞水情况下桨盘面上的动能流量与船后相等。图6中点划线与实线相交处,有Va/U=0.775,此即实效伴流分数。

图5 推力余量Fig.5 Excess thrust at three rates of rotation
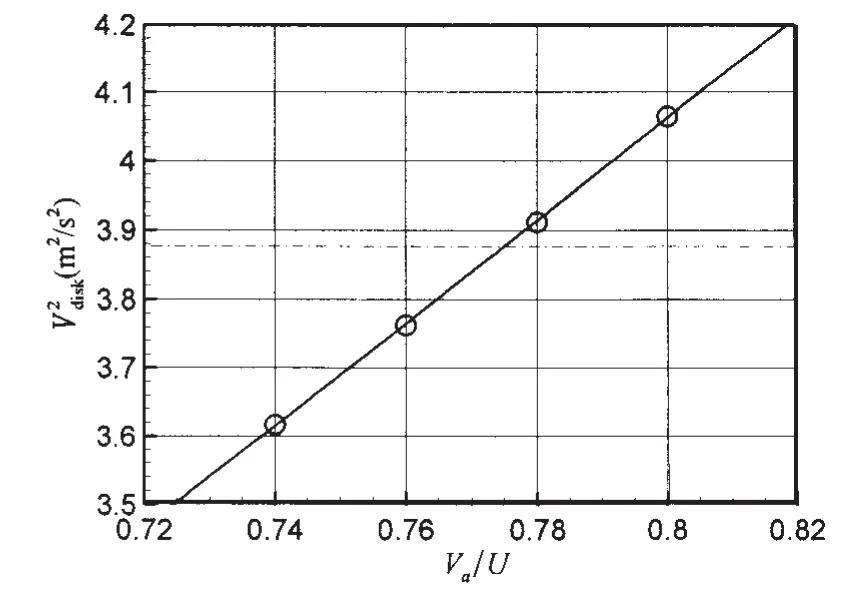
图6 桨盘面上轴向速度平方的面积平均Fig.6 Area-weighted average of axial velocity squared on the propeller disk
采用前面得到的推力T和进速Va,代入下式:

可以得到T、Va不变时KT随n的变化曲线,为了区别于敞水性征曲线,将其命名为KT′(如图7所示)。两条KT曲线相交,得到J=0.722,KT=0.166,KQ(O)=0.028 5。由J和Va计算得到转速n=9.429 rps。
表2给出了自航计算结果及其误差分析。由于采用体积力螺旋桨模型,KQ无法求出。故在推进效率的计算中假定KQ=KQ(O)。从表2可以看出,在计算实效伴流时,在敞水与自航计算之间选择轴向动能流量作为判据,并采用等推力判定,可以得到自航点上的各项数据,且计算误差都在2.9%以内。
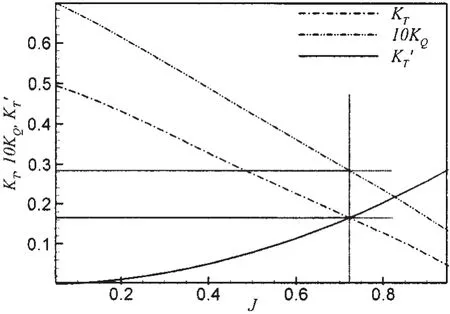
图7 螺旋桨性征曲线Fig.7 Propeller open water curves
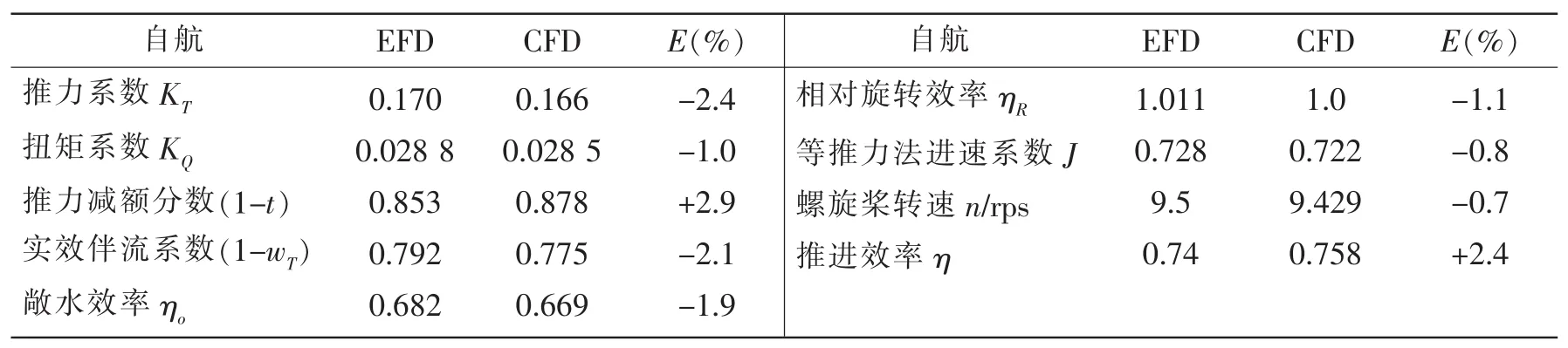
表2 计算结果及其误差分析Tab.2 Computational results and error analysis
3.2.2 扭矩的影响
上述计算都只考虑螺旋桨引起的轴向力,没有考虑扭矩。本节将引进扭矩的影响,进行全流场自航计算。并引用前第3章的算法,进一步考察算法的精度。图8给出了桨盘面下游(0.25×Dp)截面上的轴向速度等值线。由于是全流场计算,螺旋桨的旋转运动得到了充分模拟。
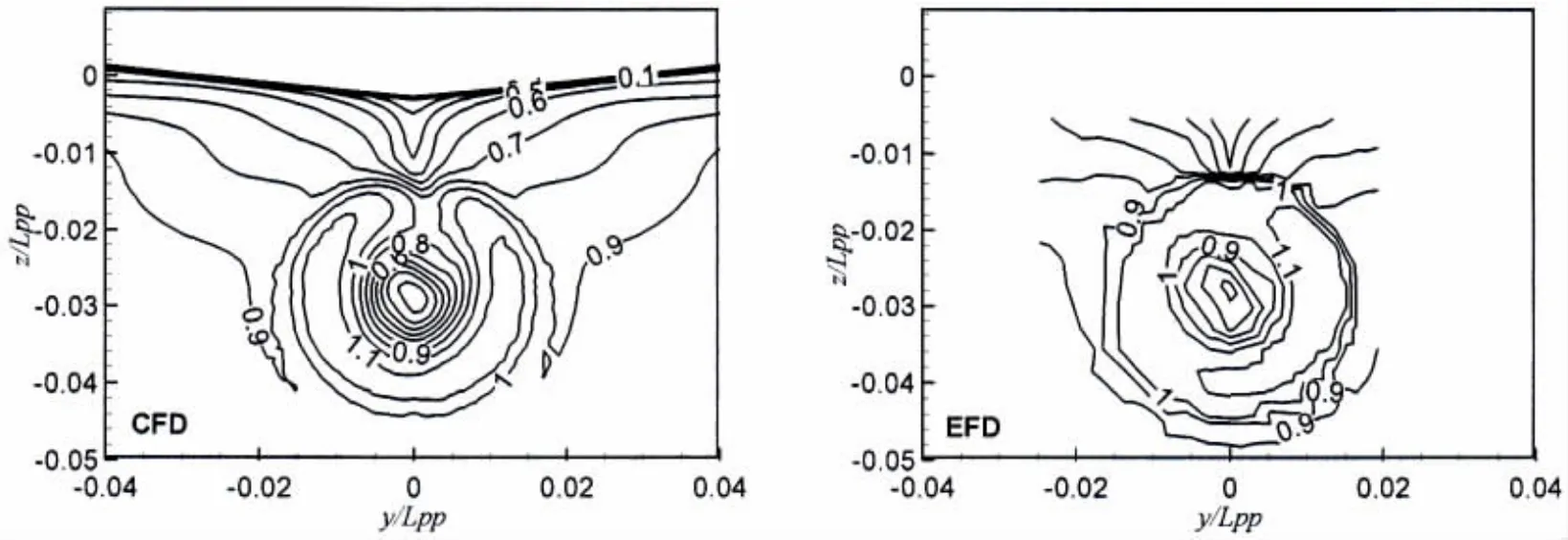
图8 桨盘面下游(0.25Dp)截面上的轴向速度Fig.8 Axial velocity contours 0.25Dpbehind the propeller plane

表3 考虑扭矩计算结果及其误差分析Tab.3 Computational results with torque

续表3
图9给出了自航条件下考虑扭矩的计算结果:船体表面压力分布及螺旋桨周围的流线。流经螺旋桨盘面后的流体形成旋转流线清晰可见。表3给出了考虑扭矩时自航计算结果及其误差分析。由于采用体积力螺旋桨模型,KQ仍然无法求出。故在推进因子的计算中仍然假定KQ=KQ(O)。从表3可以看出,考虑扭矩后,实效伴流系数及大部分参数的求解精度都略有提高,但变化不大。因此可以说本文在第3章中提出的自航计算方法,即便在不考虑扭矩时也是极其有效的。
4 结 论
本文提出了一种基于体积力螺旋桨模型的模型尺度下,实船自航点的计算方法。通过敞水及船后螺旋桨桨盘面上的动能流量相等判据得到实效伴流系数;通过等推力法得到推力系数及推进效率。仅考虑推力和同时考虑扭矩的情况下,所有自航因子的计算误差均在2.9%以内。通过波形、伴流及自航因子的分析比较,说明本次计算所采用的网格(有对称面计算是33万,全流场计算是66万)是高效的。
[1]许 晶,高秋新,周连第.实效伴流雷诺数影响的数值模拟[J].船舶力学,1999,3(1):13-20. Xu Jing,Gao Qiuxin,Zhou Liandi.Numerical simulation of Reynolds number effect on effective wake[J].Journal of Ship Mechanics,1999,3(1):13-20.
[2]张志荣,李百齐,赵 峰.螺旋桨/船体粘性流场的整体数值求解[J].船舶力学,2004,8(5):19-26. Zhang Zhirong,Li Baiqi,Zhao Feng.Integral calculation of viscous flow around ship hull with propeller[J].Journal of Ship Mechanics,2004,8(5):19-26.
[3]王金宝,蔡荣泉,冯学梅.计及自由面兴波和螺旋桨非定常旋转效应的集装箱船舶绕流场计算研究[J].水动力学研究与进展,2007,22(4):491-500. Wang Jinbao,Cai Rongquan,Feng Xuemei.Practical research on viscous flow around container ship taking into account the effect of free surface and propeller rotation[J].Journal of Hydrodynamics,2007,22(4):491-500.
[4]Kim W J,Van D H,Kim D H.Measurement of flows around modern commercial ship models[J].Experiments in Fluids, 2001,31(5):567-578.
[5]Larsson L,Stern F,Bertram V.Benchmarking of computational fluid dynamics for ship flows:The Gothenburg 2000 workshop[J].Journal of Ship Research,2003,47(1):63-81.
[6]傅慧萍,马 宁.自由面及伴流计算对网格的要求[J].上海交通大学学报,2009,43(10):1573-1576. Fu Huiping,Ma Ning.Demands of free surface and wake computation on mesh[J].Journal of Shanghai Jiao Tong University,2009,43(10):1573-1576.
[7]傅慧萍,杨晨俊.雷诺数对船舶阻力和伴流场的影响[J].上海交通大学学报,2009,43(10):1555-1558. Fu Huiping,Yang Chenjun.The effects of Reynolds number on resistance and wake of ship[J].Journal of Shanghai Jiao Tong University,2009,43(10):1555-1558.
[8]盛振邦,刘应中.船舶原理[M].上海:上海交通大学出版社,2003.
[9]Stern F,Kim H T,Patel V C,et al.A viscous-flow approach to the computation of propeller-hull interaction[J].Journal of Ship Research,1988,32(4):246-262.
Computation on self-propulsion at ship point based on a body-force propeller
FU Hui-ping1,Thad J.MICHAEL2,Pablo M.CARRICA2
(1.School of Naval Architecture,Ocean and Civil Engineering,Shanghai Jiao Tong University, Shanghai 200240,China;2.IIHR,University of Iowa,IA 52242,USA)
Based on a body-force propeller model,the viscous self-propulsion flow field with free surfaces of model-scaled KRISO container ship KCS at ship point is numerically simulated with general CFD code FLUENT 12.0.16.The computation method of self-propulsion is validated by comprehensive comparison between computational results and experimental data.The mesh used in this paper is completely structured hexahedral cells and the comparison on flow details between computed results and experimental data is good, so the 330 000 cell mesh is also proved as high effective.Both the model ship towed test and self propelled test at ship point in still water are numerically simulated.And for the self-propulsion computation,either case with or without considering torque is computed.The results show that considering torque is favorable to improve the computation accuracy and capture the flow features,but with additional computational expense.
KRISO container ship(KCS);self-propulsion computation;body-force propeller
U664.33
A
10.3969/j.issn.1007-7294.2015.07.005
1007-7294(2015)07-0791-06
2014-12-17
傅慧萍(1972-),女,副教授,E-mail:fuhp@sjtu.edu.cn;
Thad J.MICHAEL,男,博士;
Pablo M.CARRICA,男,教授。
