海洋立管悬挂状态的固有频率和振型

雷 松，郑向远，张文首，林家浩，岳前进

（1清华大学 深圳研究生院海洋学部，广东 深圳 518055；2大连理工大学运载工程与力学学部工程力学系，辽宁 大连 116023）

海洋立管悬挂状态的固有频率和振型

雷 松1，2，郑向远1，张文首2，林家浩2，岳前进2

（1清华大学 深圳研究生院海洋学部，广东 深圳 518055；2大连理工大学运载工程与力学学部工程力学系，辽宁 大连 116023）

文章把悬挂状态的立管简化为一端固定一端自由的梁模型，考虑截面性质和有效张力及质量的变化，其控制方程为变系数的四阶偏微分方程，运用微分变换方法推导了固有频率和振型的数值计算方法。通过数值算例验证了文中方法的有效性，考察了收敛速度的变化情况，讨论了立管末端的悬挂器具对固有频率和振型的影响，并结合工程实际，给出了若干海况下立管悬挂状态时在飞溅区的共振区域。

微分变换；有效张力；固有频率；振型

0 引 言

立管是海洋石油开发中连接海面浮式生产平台和水下井口的重要通道[1]，按照不同的功能又分为钻井隔水立管、注水立管、修井立管和生产立管等。在起下水作业过程中，立管处于悬挂状态，主要靠平台上的吊车及水下机器人（ROV）辅助完成，由于受上部平台运动以及波浪、流的激励发生动态变形，偏离竖直位置，可能引起立管与月池，立管与锚链及立管之间的相互碰撞，严重影响立管的结构安全和作业效率，也给海底的对接工作带来很大的难度，因此预测立管在悬挂状态的固有频率和振型有助于准确选择作业窗口期，提高作业效率[2-3]，在实际工程中有十分重要的意义。

立管一般简化为梁模型，由于立管的截面性质，有效张力及单位长度质量沿长度方向发生变化，其控制方程是一个变系数的四阶偏微分方程，很难进行解析求解[4-5]。针对类似问题，国内外学者分别采用WKB方法[6]，傅立叶分析[7]，动刚度法[8]，有限元法[9]，变量转换[10]等数值方法来计算立管服役时的固有频率和振型，而目前对立管悬挂状态的固有频率和振型研究还较少[11-12]，且其中一些数值算法的假设对新的边界条件并不适用，并不能简单加以扩展应用到立管悬挂状态；而微分变换方法[13-14]在求解类似的方程的初边值问题时特别有效，本文目的就是将这种方法运用到求解立管悬挂状态时的固有频率和振型中来，并验证了此算法的有效性及收敛速度。最后文中结合工程实际进行了参数分析和讨论。

1 力学模型的建立

1.1 控制方程

立管通常运用基于小变形假设的欧拉—贝努利梁模型[15]来模拟，即假设微元的转动量可以忽略，只关注水平位移；和弯曲变形相比，因剪切力引起的角变形是微阶小量，可予以忽略。如图1所示建立坐标系，以顶端为坐标原点，x轴为顺流向，y轴为横流向，模型在xoz和yoz平面有相似的振动形式和控制方程，本文以xoz平面为例。考虑一般情况，立管的弯曲刚度、轴向张力及单位长度质量是沿长度z方向的变化量，则悬挂状态立管的自由振动微分控制方程为：

为有效单位长度质量。

对于悬挂状态的立管，有效张力Te（z）可表示为：

立管的有效单位长度质量me（z）可表示为：

图1 立管模型及坐标系Fig.1 Coordinate system

式中：mr，mf和ma分别为立管自身的质量，立管内部流体的质量和海水引起的附加质量，暂不予考虑流体流动引起的惯性力。假设立管在xoy截面内径和外径分别为Di和Da，立管密度为ρr，流体密度为ρf，海水密度为ρw，附加质量系数为Ca，则：

悬挂状态立管边界条件为上端固定，下端自由，末端悬挂器具简化为集中质量，记为mB=WB/g，可分别根据两端的水平方向力平衡和力矩平衡，得到的四个边界条件如下：

（1）式和（5）、（6）式一起建立了立管悬挂状态时自由振动的力学模型，方程的解通常用分离变量的空间函数和时间变量函数）表示为：

运用（7）式可将（1）式和（5）、（6）式转化为常微分方程。

1.2 无量纲化

为了使控制方程更具有一般性，可定义以下变量对转化后的常微分方程进行无量纲化：

式中：ω为立管的圆频率。根据（7）式和（8）式，（1）式可写为：

相应地，四个边界条件可写为：

2 微分变换方法的运用

2.1 微分变换的定义[9-11]

微分变换还有一些基本性质，如线性性质，乘积性质，微分性质等可参见文献[9-11]。

2.2 应用求解

运用微分变换和它的基本性质，常微分方程式（9）经转化为代数方程：

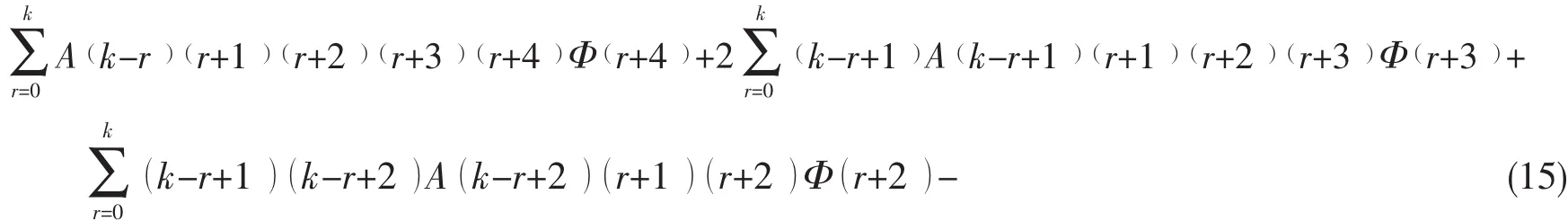
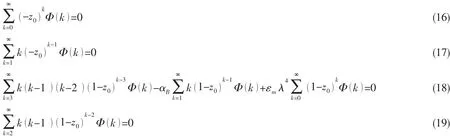
（20）式有非平凡解，则需满足：

（21）式为一个关于λ的高次代数方程，可用数值的方法求出λ。结合（8）式，则立管的频率为：

求出立管的频率后，就很容易得到立管振型。先假定χ0=1，把求得的λ代入（20）式，可求得χ1，χ2和χ3；有了χ0—χ3，便可利用递推关系（15）式依次求出Φ（k）；再用微分逆变换（13）式即可求出振型，并可根据（23）式对振型进行归一化。

3 算 例

3.1 立管的基本参数

以文献[8]中常用的钻井隔水立管起下水作业为例进行数值分析，假设截面和材料性质在长度方向保持一致，只考虑有效张力的变化，立管的外径Do=0.558 8 m，内径Di=0.508 0 m，密度为ρr=7 850 kg/m3，抗弯刚度EI=3.186 0×108N·m2，表观重力w=3 433.5 N/m，内部流体密度为ρf=1 200 kg/m3，外部海水密度为ρw=1 025 kg/m3，附加质量系数为Ca=1，末端悬挂器具的质量mB=8.4×104kg。根据这些参数，则其控制方程式（9）可写为：

结合边界条件（16）-（19）式，利用（20）-（23）式便可求出立管的固有频率和振型。

3.2 结果与分析

3.2.1 算法验证与收敛速度

首先通过与有限元结果的对比来验证此算法的有效性。以立管下水长度L为100 m即σ=36.641 2，η=10.776 8，εm=1.013 6时为例，表1给出了两种不同方法的计算结果，从表中可以看出两种方法的计算结果吻合；而有限元的计算结果易受划分单元数目影响，而微分变换方法的结果在理论上接近精确解，且便于进行参数分析。

微分变换方法是一种迭代算法，计算的收敛速度决定了迭代的次数，也就是（14）式中所需的展开项数，取立管下水长度L为100 m，收敛精度为0.000 1，考察其收敛速度。图2给出了取不同的展开项时前四阶频率的计算结果，图 2（a）中一阶频率在取25项后收敛值为0.330 6 rad/s，图 2（b）中二阶频率取27项后收敛值为1.591 6 rad/s，图2（c）中三阶频率取33项后收敛值为3.895 9 rad/s，图2（d）中四阶频率取39项后收敛值为7.337 7 rad/s。从中可以推断，计算更高阶频率需要更多的展开项，计算时间也相应增长。

图3考察了立管在不同长度时计算前四阶频率所需最小展开项的变化情况，从图中可以看出计算一阶频率所需的展开项与立管的长度大致呈线性关系，随着长度的增加，所需最小展开项从L=20 m时的10项增大到L=200 m时的47项；二阶至四阶频率在长度L＞80 m后，所需最小展开项也呈现线性增大的趋势。图4给出了计算前四阶频率所需时间与长度之间的变化关系，所用计算机处理器主频为2.4 GHz。长度为20 m时所需时间为27.863 1 s，长度为200 m时所需时间增大为152.224 5 s，从中可以看出立管长度增大时，因所需展开项增多，耗费机时增加，且增长速度越来越快。

图3 最小展开项与长度之间的变化关系Fig.3 Relationship between least number of expansion terms and riser length

图4 计算时间与长度之间的变化关系Fig.4 Relationship between computing time and riser length

图5 两种工况下立管的前两阶频率Fig.5 First two modal frequencies of risers under two different conditions

3.2.2 参数分析

通过两种工况比较末端悬挂器具对立管模态的影响。工况1：立管末端悬挂器具下水，即σ=（wL+工况2：未悬挂器具下水，即图 5给出了这两种工况下立管的前两阶频率随长度的变化情况。从横向对比来看，随着立管长度的增大，两种工况下立管的固有频率都呈现降低的趋势。纵向对比可以发现，随着长度的增大，工况1的计算结果出现先小于工况2，然后等于工况2，再大于工况2的现象。出现这种现象是因为末端悬挂器具对立管性质有两方面的影响，一方面增加立管的轴向张力，相当于增加立管刚度；另一方面又增加了立管的质量。在立管长度较小时，增加质量的因素起主导作用，引起频率减小；长度增大后，增加刚度的因素起主导作用，引起频率增大。

图6对比了L=100 m时两种工况下的归一化振型，从图中可以看出，两种工况下的振型形状相似，悬挂器具后，振型形状整体向下偏移，对上半段影响尚不明显，但对下半段有较大影响，使高阶振型中波腹点位置向下移动，且曲率减小。此外，工况1时立管振型的末端更加靠近中轴线位置，这是因为末端的集中质量相当于增加了约束，限制了立管尾段的位移。

图6 两种工况下的前四阶振型Fig.6 First four mode shapes of riser under two different conditions

3.2.3 共振区域

在起下水作业过程中，立管从海面浮体上逐渐下放至海底。在此过程中，立管在位于水平面附近的飞溅区承受较大的周期性波浪荷载，随着入水长度增加，若立管的固有频率接近波浪的频率时就会引起共振现象，导致立管顶部因弯矩过大而失效。波浪以常用的P-M谱为例，讨论立管起下水过程中可能的共振区域。图7给出了P-M谱中有义波高Hs为3 m时的波浪谱曲线，其中95%的能量集中在红色区域和ωH可根据文献[16]求得，把此区间当作波浪激励频率，对比立管的固有频率，就可以得到共振区域。

针对工况1，立管在3种不同海况条件下的共振区域如表 2所示，从表中可以看出，在飞溅区易发生一阶和二阶共振。在有义波高为3 m的时候，立管的一阶共振发生在入水长度为15-50 m处，二阶共振发生在85-270 m处；在有义波高为4 m的时候，立管的一阶共振发生在水下18-60 m处，二阶共振发生在95-325 m；在有义波高为5 m的时候，立管的一阶共振发生在水下20-70 m处，二阶共振发生在105-380 m。从表中也可以看出随着有义波高的增大以及波浪的激励频率上限和下限分别降低，对应立管的共振区域有所增大。

图7 P-M谱Fig.7 P-M spectrum

表2 不同海况条件下的共振区域Tab.2 Resonance zone in different sea states

4 结 论

本文运用微分变换方法求解立管自由悬挂状态的固有频率和振型,以常用的钻井隔水立管起下水作业为例，通过数值算例可得到如下结论：

（1）微分变换的方法可以用来计算立管的固有频率，取得收敛结果，收敛速度随着立管长度的增大大致呈线性增长的趋势。

（2）钻井隔水立管起下水作业时，末端的悬挂器具在浅水时减小了立管固有频率，随着水深增大又增大了立管的固有频率；末端的悬挂质量同时影响立管下半段的振型，使末端更靠近平衡位置。

（3）立管携带器具起下水过程中，在飞溅区易发生一阶和二阶共振，共振区域随有义波高的增大而增大。

[1]Bai Yong,Bai Qiang．Subsea Pipelines and Risers[M]．Great Britain:Elsevier Science Ltd,2005:401-408.

[2]Zhang Qi,Yang Hongbiao,Huang Yi,Zhang Rixi.Effect of several key parameters on the dynamic analysis of TTR[J]. Journal of Ship Mechanics,2012,16(3):296-306.

[3]姜 伟．深水钻井隔水导管在起下作业过程中的固有频率研究[J]．中国海上油气,2010,22(1):37-41. Jiang Wei.Study on natural frequency of deepwater drilling riser during down and up operations[J].China Offshore Oil and Gas,2010,22(1):37-41.

[4]Jaroszewicz J,Zoryi L,Jaroszewicz J,et al.Investigation of the effect of axial loads on the transverse vibrations of a vertical cantilever with variable parameters[J].International Applied Mechanics,2000,36(9):1242-1251.

[5]张 杰,唐友刚.深海立管固有振动特性的进一步分析[J].船舶力学,2014,18(1):165-171. Zhang Jie,Tang Yougang.Further analysis on natural vibration of deep-water risers[J].Journal of Ship Mechanics,2014, 18(1):165-171.

[6]Kim Y C,Triantafyllou M S.The nonlinear dynamics of long slender cylinders[J].Journal of Energy Resources Technology,1984,106(2):250-256.

[7]Soltanahmadi A.Determination of flexible riser natural frequencies using Fourier analysis[J].Marine Structures,1992,5: 193-203.

[8]Cheng Y,Vandiver J K,Moe G.The linear vibration analysis of marine risers using WKB-based dynamic stiffness method [J].Journal Sound and Vibration,2002,251(4):750-760.

[9]Park H I,Jung D H.A finite element method for dynamic analysis of long slender marine structures under combined parametric and forcing excitations[J].Ocean Engineering,2002,29:1313-1325.

[10]Sparks C P．Transverse modal vibrations of vertical tensioned risers:a simplified analytical approach[J]．Oil&Gas Science and Technology,2002,57(1):71-86.

[11]Virgin L N,Santillan S T,Holland D B.Effect of gravity on the vibration of vertical cantilevers[J].Mechanics Research Communications,2007,34(3):312-317.

[12]Xi L Y,Li X F,Tang G J.Free vibration of standing and hanging gravity-loaded Rayleigh cantilevers[J].International Journal of Mechanical Sciences,2013,66:233-238.

[13]Mei C．Application of differential transformation technique to free vibration analysis of a centrifugally stiffened beam[J]．Computers&Structures,2008,86:1280-1284.

[14]Chen Yanfei,Chai Y H,Li Xin,Zhou Jing．An extraction of the natural frequencies and mode shapes of marine risers by the method of differential transformation[J]．Computers&Structures,2009,87:1384-1393.

[15]Meirovith L.Principles and techniques of vibrations[M].Englewood cliffs:Prentice Hall,1997.

[16]俞聿修.随机海浪及其工程应用[M].大连:大连理工大学出版社,2000.

Natural frequencies and mode shapes of free-hanging risers

LEI Song1,2,ZHENG Xiang-yuan1,ZHANG Wen-shou2,LIN Jia-hao2,YUE Qian-jin2
(1 The Division of Ocean Science and Technology,Tsinghua University Shenzhen Graduate School, Shenzhen 518055,China;2 Faculty of Vehicle Engineering and Mechanics,Dalian University of Technology,Dalian 116023,China)

Free-hanging risers are simulated as Euler-Bernoulli beams with fixed-free boundary conditions. Considering varying flexural rigidities,effective tensions and mass density,free vibration of the riser is expressed in form of fourth order partial differential equation with variable coefficient whose analytic solution is not straightforward.The natural frequencies and mode shapes are obtained by using differential transformation method.The efficiency of this method and its good convergence rate are validated by numerical examples.Furthermore,the influence of a lumped mass at riser tip is discussed.Resonance zones,which are important during the installation of risers at the wave splash zone,are illustrated.

differential transformation;effective tension;natural frequency;mode shape

O175.2

A

10.3969/j.issn.1007-7294.2015.10.012

1007-7294（2015）10-1267-08

2015-04-29

中国博士后科学基金（2015M571043）；国家创新研究群体科学基金（5092100）

雷 松（1982－），男，博士后，E-mail:leisong1982@sz.tsinghua.edu.cn；郑向远（1975－），男，研究员。