半潜平台内孤立波载荷特性数值模拟

王 旭，林忠义，尤云祥

（1上海交通大学 海洋工程国家重点实验室，上海 200240；2嘉兴南洋职业技术学院，浙江 嘉兴 314003）

半潜平台内孤立波载荷特性数值模拟

王 旭1，林忠义2，尤云祥1

（1上海交通大学 海洋工程国家重点实验室，上海 200240；2嘉兴南洋职业技术学院，浙江 嘉兴 314003）

以三类内孤立波理论KdV、eKdV和MCC的适用性条件为依据，采用Navier-Stokes方程为流场控制方程，将内孤立波诱导上下层深度平均水平速度作为入口边界条件，建立了两层流体中内孤立波对半潜平台强非线性作用的数值模拟方法。结果表明，数值模拟所得内孤立波波形及其振幅与相应理论和实验结果一致，并且在内孤立波作用下半潜平台水平力、垂向力及其力矩数值模拟结果与实验结果吻合。研究同时表明，半潜平台内孤立波载荷由波浪压差力、粘性压差力和摩擦力构成，其中摩擦力很小，可以忽略；水平力的主要成分为波浪压差力和粘性压差力，粘性压差力与波浪压差力相比较小却不可忽略，流体粘性的影响较小；垂向力中粘性压差力很小，流体粘性影响可以忽略。此外，半潜平台对内孤立波的波形及其诱导流场的影响很小，因此采用Morison和傅汝德—克雷洛夫力公式计算其内孤立波载荷是可行的。

两层流体；内孤立波；半潜平台；载荷特性

0 引 言

内孤立波是一种最大振幅发生在密度稳定层化海洋内部的波动，由于非线性和色散效应在一定尺度上的平衡，在其传播过程中可以保持波形和传播速度不变，一般地可以用KdV（Korteweg-de Vries）、eKdV（extended KdV）和MCC（Miyata-Choi-Camassa）等理论模型来描述。在KdV理论中要求内孤立波是弱非线性、弱色散且两者平衡的，而在eKdV理论中只要求内孤立波是弱非线性和弱色散的[1]。为克服需要弱非线性限制条件的缺陷，Choi和Camassa[2]建立了强非线性和弱色散的内孤立波理论，称为MCC理论。但在这三类理论中弱非线性和弱色散这两个条件仅仅为定性描述，为此黄文昊等[3]以系列实验为依据给出了这两个条件的定量表征方法。

我国南海海域海洋环境条件复杂且海水密度垂向层化现象显著，内孤立波活动频繁，1990年，在流花油田就曾发生过因内孤立波导致缆绳拉断、船体碰撞，甚至拉断和挤破漂浮软管的事故[4]。同年，在南海陆丰油田也发生过因内孤立波导致半潜钻井船与锚定油轮在连接输油管道时发生困难等问题[5]。因此，内孤立波已成为南海油气资源开发工程中面临的特有灾害性环境因素之一。

由于具有性能优良、抗风浪能力强、甲板面积大、适应水深范围广等优点，深海半潜式平台将是我国南海深海资源开发中首选的海洋工程装备之一，而合理确定各种海洋环境条件下半潜平台的载荷特性则是深海半潜平台设计和应用中的一项关键问题。程友良等[6-9]将Morison公式与KdV理论结合，研究了内孤立波作用下小尺度杆件的载荷特性问题。尤云祥等[10-11]将Morison公式与eKdV理论结合，研究了内孤立波作用下张力腿和半潜式平台的载荷与动力响应问题。需要指出的是，在这些文献中，关于Morison公式中惯性力和拖曳力系数都是参照表面波的方法选取的，但这种选取方法缺乏理论和实验依据。为此，黄文昊等[12]以系列实验为依据针对半潜平台给出了这两个系数的选取方法。

由此可见，对内孤立波作用下深海平台载荷问题，许多机理性的问题尚不清楚，包括各种内孤立波载荷成分的形成机理，流体粘性对内孤立波载荷的影响机理，以及利用Morison公式求解深海半潜平台内孤立波载荷的合理性等。计算流体力学（Computational Fluid Dynamics，简称CFD）方法为进一步深入认识这些问题提供了一条有效的途径。采用CFD方法可以直接获得内孤立波与深海半潜平台强非线性相互作用过程中的流场变化特性，因此可以直接获得内孤立波作用下深海半潜平台载荷等水动力特性。

关辉等[13]基于KdV理论，而高原雪等[14]基于MCC理论，采用CFD方法研究了内孤立波的生成传播问题。刘碧涛等[15]基于eKdV理论，采用CFD方法分别研究了内孤立波作用下海洋立管的载荷特性等问题。需要指出的是，在这些文献中，由于没有考虑KdV、eKdV和MCC理论的适用性条件，致使其数值模拟结果均不同程度地出现了内孤立波振幅及其波形不可控等问题。因此，如何选择合适的内孤立波理论作为CFD数值模拟的依据，则是在采用CFD方法研究其生成传播及其对海上结构物强非线性作用特性问题时需要解决的关键问题。

有鉴于此，本文采用 Navier-Stokes方程，依据文献[3]确定的三类内孤立波理论KdV、eKdV和MCC的适用性条件，建立振幅及其波形可控的内孤立波CFD数值模拟方法。在此基础上，对内孤立波与半潜平台的相互作用特性进行数值模拟，进而分析内孤立波作用下半潜平台各种载荷成分的形成机理及其影响程度，半潜平台对内孤立波的波形及其流场的影响，以及使用Morison公式等简化方法计算半潜平台内孤立波载荷的合理性等问题。

1 数值方法

设各层均为不可压流体，上层流体深度与密度分别为h1和ρ1，下层流体深度与密度分别为h2和ρ2。建立直角坐标系oxyz，其中oxy平面位于流体静止时两层流体的界面上，oz轴与半潜平台垂向中心轴重合且垂直向上为正。内孤立波为平面前进波，界面位移为ζ，沿ox轴正方向传播。流场计算的控制区域如图1所示，包括内孤立波生成传播区（图中非阴影区域）和消波区（图中阴影区域）两个区域。采用速度入口方法生成内孤立波，当造波区中形成稳定的内孤立波后，对所生成内孤立波的传播特性进行监测分析，并对半潜平台的内孤立波载荷进行计算。

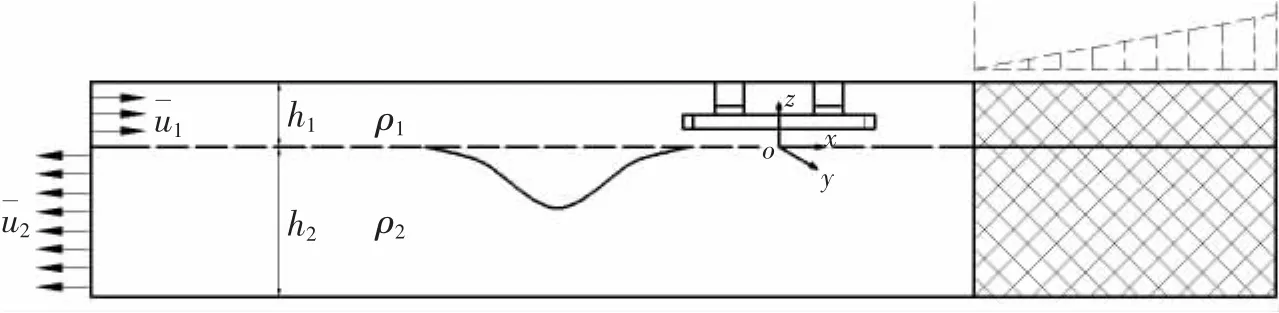
图1 内孤立波数值水槽示意图Fig.1 Sketch of the numerical flume for the internal solitary waves

采用Navier-Stokes方程对内孤立波诱导流场进行数值模拟，流场控制方程为：

半潜平台壁面取为无滑移边界条件，而计算域顶部及底部要求满足如下壁面条件：

设内孤立波振幅为a，相速度为c，则其诱导上下层流体中的层深度平均水平速度分别为[2]：

半潜平台的内孤立波水平力由摩擦力和压差力两个部分组成，如下式所示：

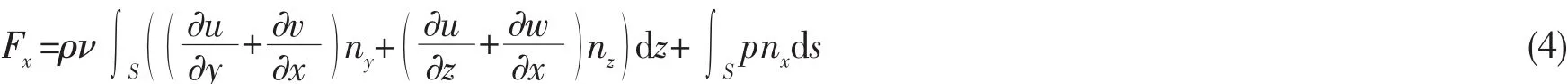
半潜平台的内孤立波垂向力同样由表面摩擦力和压差力组成，如下式所示：

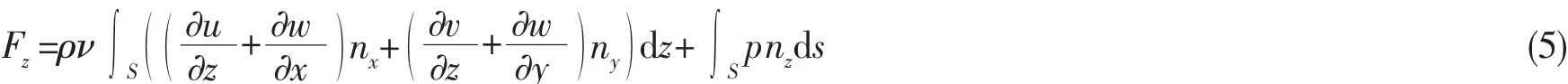
其中：S为半潜平台浸湿侧表面积，式中第一项为半潜平台侧表面和底部的载荷摩擦力；第二项为半潜平台侧表面的载荷压差力，为半潜平台表面法向矢量，正方向指向半潜平台内部。

内孤立波作用于半潜平台的力矩可表示为

其中：力矩转动中心至平台底部距离为d¯，在顺时针时My为正，在逆时针时My为负。

在数值模拟中，如何选择合适的内孤立波理论来计算入口速度是一个需要解决的关键问题。根据文献[3]定量确定的三类内孤立波的适用性条件，入口速度（3）的计算方法如下：

利用商业软件Fluent进行数值模拟与分析。采用有限体积法离散动量和连续性方程，对流项采用QUICK（quadratic upstream interpolation for convective kinetics）离散格式，压力插值格式采用体积力加权（body force weighted）方法，压力速度耦合迭代采用PISO（Pressure Implicit with Splitting of Operators）算法，两层流体界面的构造方法选用几何重构法。初始时间步长为Δt=0.005 s，计算过程中根据每个时间步长的收敛情况逐渐增加时间步长以缩短计算时间。

2 结果与分析

文献[12]利用大型密度分层水槽，对内孤立波作用下半潜平台模型的载荷特性进行了系列实验，本文将结合该文献中的相关实验结果进行数值模拟与分析。为此，数值水槽主尺度、上下层流体密度及其深度比均与该文一致。其中，数值水槽长度为30 m，水深为1 m，上下层流体密度分别为ρ1=998 kg/m3和ρ2=1 025 kg/m3，上下层流体深度比分别选择h1:h2=1:9、2:8和3:7三种密度分层工况。

半潜平台模型以“海洋石油981”深水半潜式钻井平台为原型，缩尺比为：1:300，平台模型水下部分如图2所示，模型主尺度为甲板长258 mm，宽248 mm；立柱高71.5 mm，最宽部分的横截面尺寸为58 mm×58 mm；底部浮箱长380 mm，宽67 mm，高28.5 mm；横撑长142 mm，横截面8 mm×6 mm。吃水d=0.063 m，半潜平台重心距速度入口端9 m。

2.1 内孤立波数值模拟结果

利用CFD方法对内孤立波生成传播特性进行数值模拟与分析。首先研究流体粘性对内孤立波生成与传播特性的影响。为此，在数值模拟中设计如下两种情况：一种为考虑流体粘性的情况，依据Navier-Stokes方程求解，称为N-S模拟；另一种为不考虑流体粘性的情况，依据Euler方程求解，称为Euler模拟。

图3给出了当h1:h2=20:80和ad/h=0.106时（ad为内孤立波设计振幅），采用上述两种方式对内孤立波生成与传播特性的数值模拟结果。由图可知，内孤立波在向右传播过程中，在有粘和无粘两种情况下，数值模拟所得内孤立波在其传播过程中均保持波形稳定、振幅衰减很小(两者振幅相对误差均在5%以内)，没有明显的尾波现象。因此对内孤立波的CFD数值模拟，采用基于N-S和Euler方程的两种方法均是可行的，粘性对内孤立波生成与传播过程的影响较小。在下文中，如无特别声明，所有数值模拟均是在有粘情况下进行的。

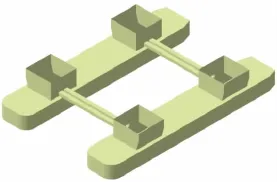
图2 半潜平台模型(水下部分)示意图Fig.2 Sketch of the submerged regions for the semi-submersible platform model

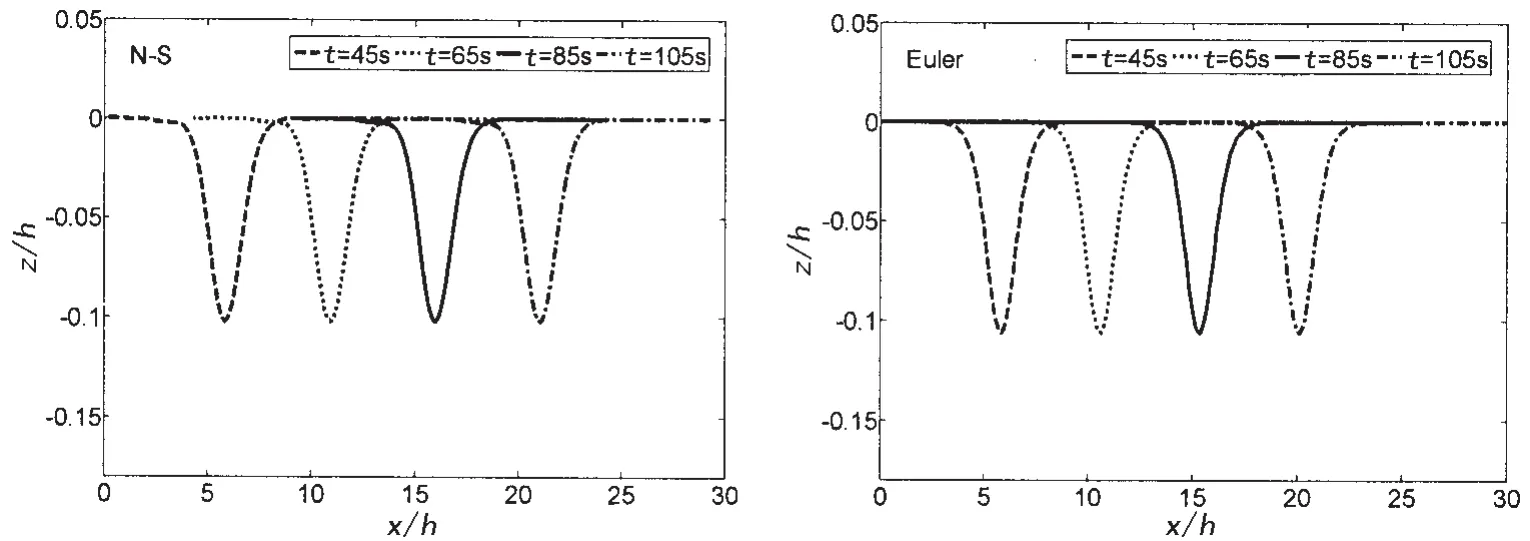
图3 当h1:h2=20:80和ad/h=0.106，在两种情况下内孤立波数值模拟结果Fig.3 The numerical results for the internal solitary waves in two different cases when h1:h2=20:80,ad/h=0.106

在图4中，给出了密度分层为h1:h2=2:8时三种不同工况下，内孤立波波形的数值模拟结果，并与相应理论和实验结果进行了比较，图中实验结果取自文献[12]。其中，工况Case A无因次设计振幅为ad/h=0.053，此时内孤立波为弱非线性和弱色散的，选择KdV理论计算入口速度；工况Case B无因次设计振幅为ad/h=0.106，此时内孤立波为中等非线性和弱色散的，选择eKdV理论计算入口速度；工况Case C无因次设计振幅为ad/h=0.225，此时内孤立波为强非线性和弱色散的，选择MCC理论计算入口速度。结果表明，在各工况下，数值模拟所得内孤立波的波形，不仅与内孤立波理论解波形一致，而且与实验所得波形吻合，这表明依据三类内孤立波理论的适用性条件，采用本文所述数值模拟方法所得内孤立波的波形是准确可控的。

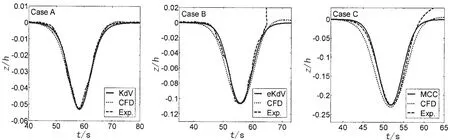
图4 内孤立波波形数值模拟结果与理论和实验结果比较Fig.4 Comparisons of the numerical results for the internal solitary wave waveforms with theoretical and experimental ones

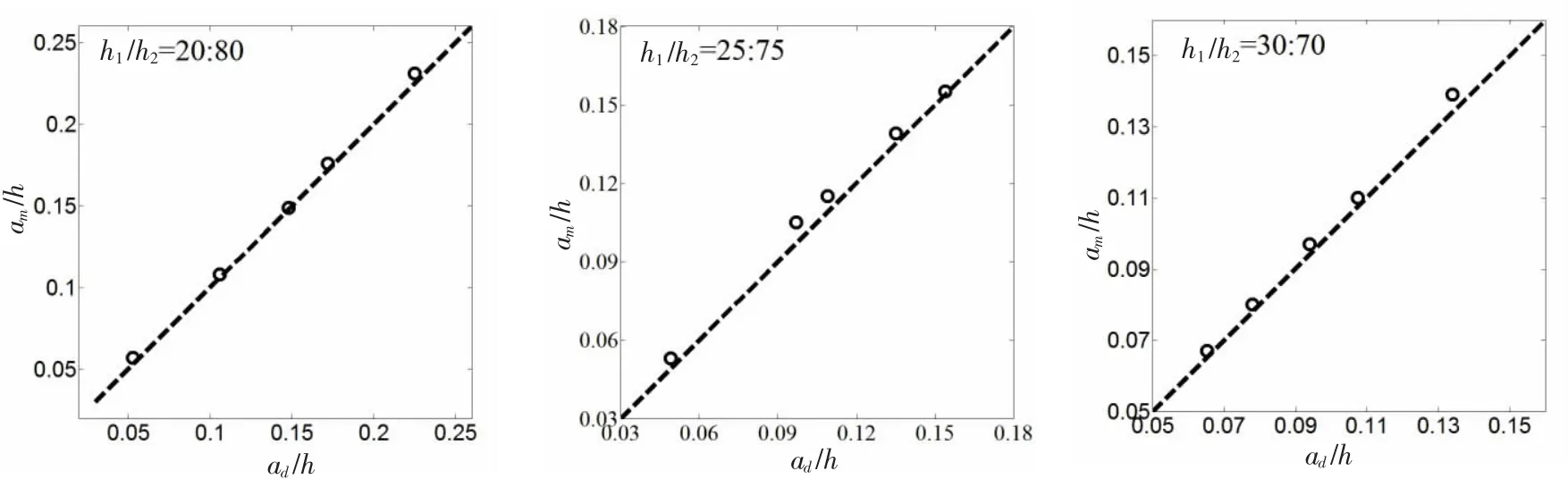
图5 内孤立波振幅数值模拟结果Fig.5 The numerical results of the waves amplitudes for the internal solitary waves

在图5中，给出了当h1:h2=20:80、25:75和30:70时内孤立波数值模拟振幅am与其设计振幅ad之间相关关系的结果。图中，横向坐标轴和纵向坐标轴分别为无因次设计振幅和无因次模拟振幅，圈号“О”表示数值模拟振幅，虚线表示设计振幅（其斜率为1），圈号与虚线之间的垂向距离表示两者之间的绝对误差。结果表明，在各数值模拟工况下，数值模拟所得内孤立波振幅均与其相应设计振幅符合较好，两者之间的相对误差不超过5%。这表明依据三类内孤立波理论的适用性条件，采用本文所述数值模拟方法所得内孤立波的振幅同样是准确可控的。

2.2 内孤立波载荷特性

图6内孤立波无因次水平力、垂向力及其力矩幅值数值与实验结果Fig.6 Results of numerical and experimental amplitudes for dimensionless horizontal and vertical forces, as well as torques due to internal solitary waves

图7给出了在Case B工况下，内孤立波无因次水平力、垂向力及其力矩时历的数值模拟结果，并与文献[12]中的实验结果进行了比较。

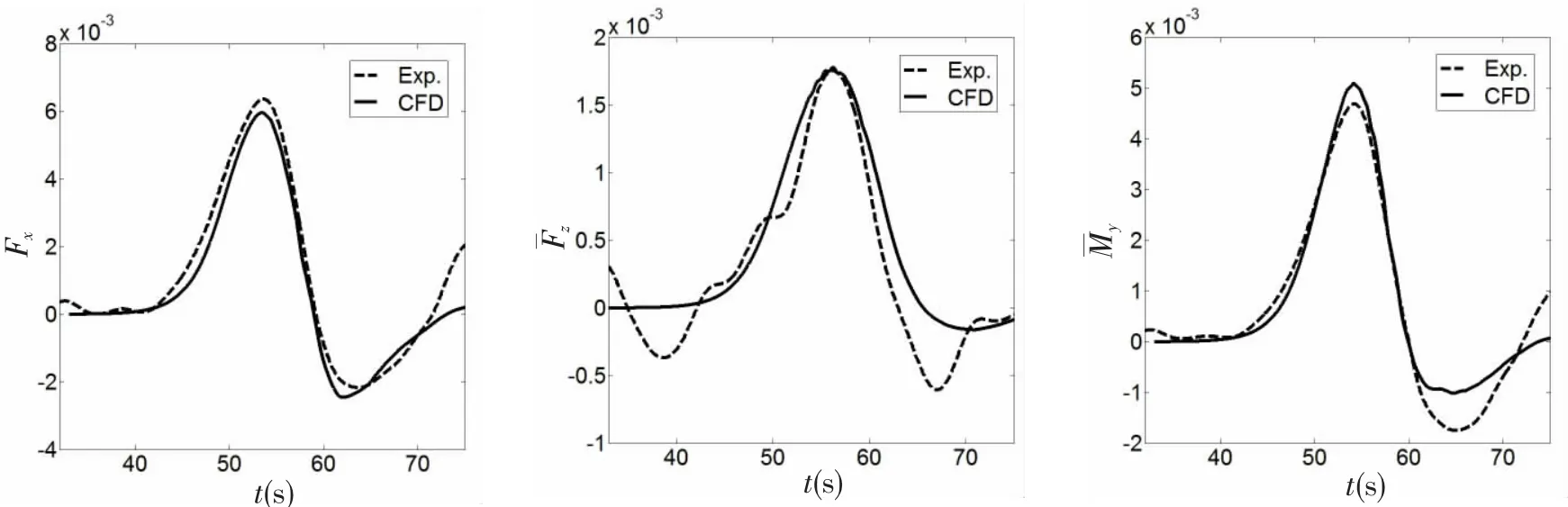
图7 在Case B工况下，内孤立波无因次水平力、垂向力及力矩时历特性Fig.7 The time-variant characteristics for dimensionless horizontal and vertical forces, as well as torques due to the internal solitary wave for Case B

由图可知，半潜平台内孤立波载荷时历数值结果与实验时历结果吻合，表明采用本文所述半潜平台内孤立波载荷的计算方法合理可行。

半潜平台内孤立波水平和垂向力两者均由压差力和摩擦力两部分构成。在图8中，给出了Case B工况下，内孤立波无因次水平压差力及其摩擦力fx的时历曲线，无因次垂向压差力及其摩擦力fz的时历曲线，其中1e2和1e4分别表示1.0×102和1.0×104。结果表明，无论是半潜平台内孤立波水平力还是垂向力，摩擦力与压差力相比都是一个小量，可以忽略，这意味着半潜平台内孤立波水平和垂向力的主要成分为压差力。

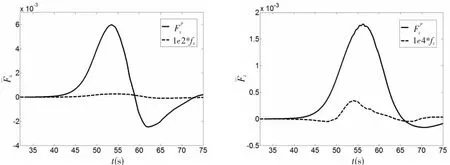
图8 在Case B工况下，内孤立波无因次压差力及摩擦力时历特性Fig.8 The time-variant characteristics for the pressure difference and the frictional forces due to the internal solitary wave for Case B

根据压差力中粘性的贡献，可以进一步将内孤立波水平和垂向压差力分为波浪压差力和粘性压差力两个部分。其中，前者波浪压差力与内孤立波诱导的水质点波动有关，认为与粘性无关，可以采用Euler模拟方法得到。而后者粘性压差力为由于流体粘性效应导致的压差力的增加，可以将N-S模拟所得压差力减去波浪压差力从而得到。在图9中，给出了在Case B工况下，内孤立波无因次水平波浪压差力及其粘性压差力，无因次垂向波浪压差力及其粘性压差力时历曲线。结果表明，对于半潜平台内孤立波水平压差力，主要成分为波浪压差力和粘性压差力，但粘性压差力与波浪压差力相比幅值较小；对于半潜平台内孤立波垂向压差力，其粘性压差力与波浪压差力相比是一个小量，可以忽略。这意味着半潜平台的内孤立波水平力中粘性效应较小却不可忽略，但对其垂向力则可以忽略流体的粘性效应。

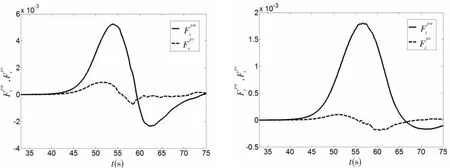
图9 在Case B工况下，内孤立波无因次波浪压差力及粘性压差力时历特性Fig.9 The time-variant characteristics for the waves and viscous pressure forces due to internal solitary waves for Case B

2.3 半潜平台对内孤立波的影响

图10给出了模拟工况为Case B时不同时刻半潜平台对内孤立波波形的影响。时间t=42 s和54 s时，半潜平台中心轴位于内孤立波谷前方；时间t=56 s时，半潜平台中心轴位于内孤立波谷所在位置；时间t=58 s和70 s时，半潜平台中心轴位于内孤立波谷后方。结果表明，在内孤立波向半潜平台传播过程中，波面始终保持稳定，位于上层流体中的半潜平台对内孤立波的波面的影响可以忽略。

图10在Case B工况下，半潜平台对内孤立波波形的影响Fig.10 The effects of the semi-submersible platform on the internal solitary wave waveform for Case B

图11给出了模拟工况为Case B，时间为t=56 s时内孤立波诱导流场特性的数值模拟结果。结果表明，在内孤立波传播过程中，其诱导的水平速度在波面上的方向与内孤立波传播方向一致，而在波面下方则方向相反，在波面上下方形成水平剪切流动；内孤立波所诱导的垂向流动，在波谷前方的垂向速度方向向下，而在波谷后方则相反；内孤立波诱导水平速度在波面上下方流体层中沿垂向的衰减很小；结合（3）式可知，由于上层流体深度小于下层流体深度，在波面上方的水平速度值要大于波面下方的水平速度值。

图12给出了Case B工况下三个不同时刻（t=54 s、56 s和58 s）时，在半潜平台附近两个不同垂向断面（z/h=0.19和0.14）速度场及其涡量场的数值模拟结果，选取的两个断面分别位于支柱及浮箱所在垂向位置。其中，各断面长度均为1.6L，而宽度均为1.2L（其中L为半潜平台底部浮箱长度）。由图可知，在内孤立波传播过程中，半潜平台对其诱导流场产生绕流作用，在半潜平台尾部形成一对旋转方向相反的尾涡。由于水平断面（z/h=0.19和0.14）位于内孤立波波面上方，其诱导水平速度方向自左向右，因此尾涡在半潜平台后方区域。

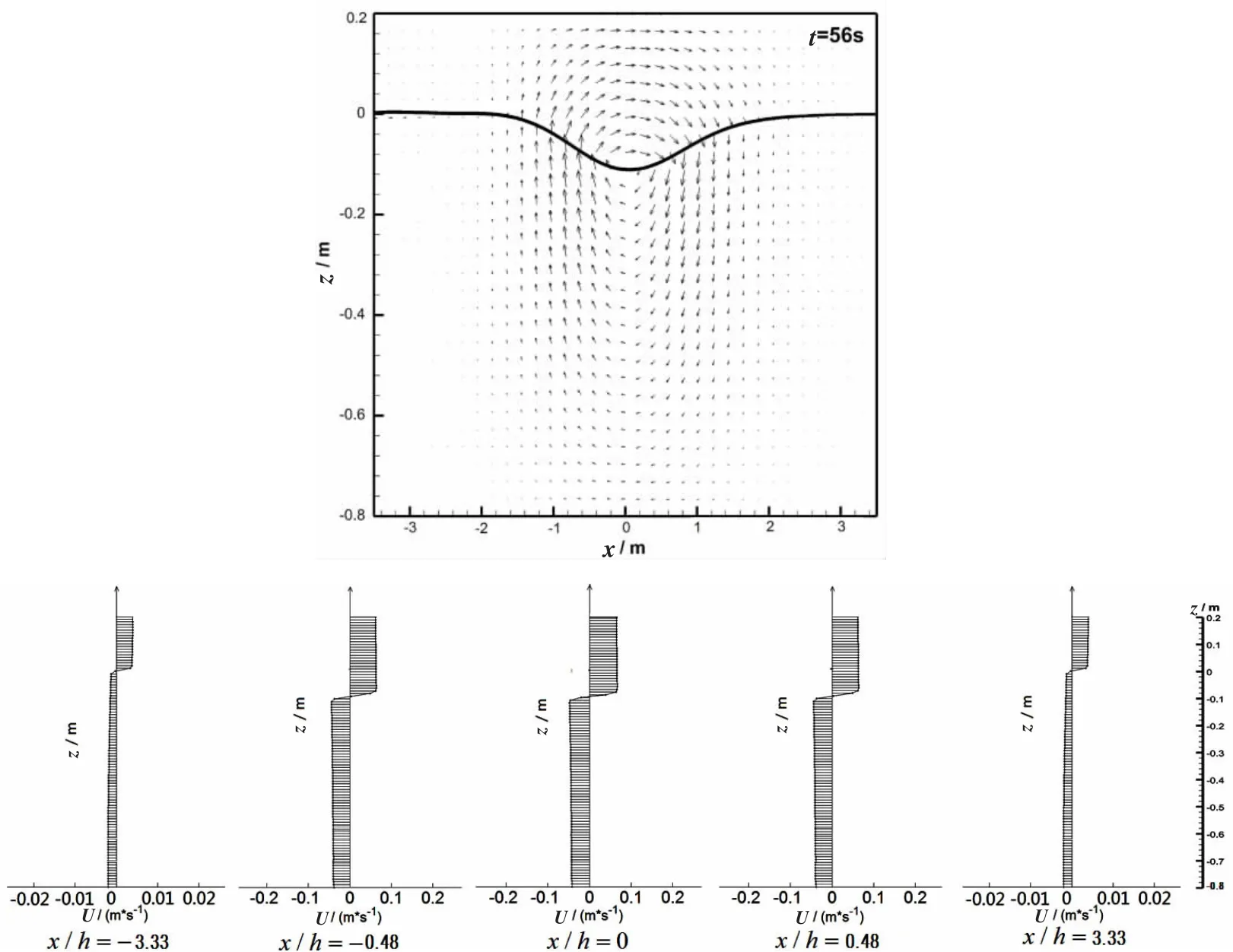
图11 在Case B工况下，当t=60 s时，内孤立波诱导流场特性Fig.11 The flow field characteristics due to the internal solitary wave when t=60 s for Case B

图12 在Case B工况下，半潜平台对内孤立波诱导流场的影响Fig.12 The effects of the semi-submersible platform on the flow field due to the internal solitary wave for Case B

众所周知，在一定雷诺数Re条件下，对圆柱体结构的定常绕流，在其尾部会形成周期性的泄涡，对柱体产生横向周期性脉动升力，并导致所谓的涡激振动现象，从而对圆柱体结构造成疲劳和断裂等破坏。内孤立波诱导流场在流经半潜平台时也会产生泄涡现象，这种泄涡现象对半潜平台同样将会产生升力作用。为此需要特别考虑该升力的时历特性，设Fy为作用在半潜平台上的升力，其无因次量定义为。图13给出了Case B工况下半潜平台无因次升力时历特性，由图可知，内孤立波诱导流场对半潜平台产生的升力是一个小量，其影响可以忽略。

数值结果表明，半潜平台的存在对内孤立波波形及其诱导流场的影响可以忽略，而且对内孤立波作用下半潜平台水平力的主要成分为波浪压差力和粘性压差力，而垂向力的主要成分为波浪压差力，前者正好可以采用Morison公式进行计算，而后者正好可以用傅汝德—克雷洛夫力进行计算。下面讨论采用这种简化方法计算半潜平台内孤立波载荷的可行性。为此，记U1和W1分别为当ζ＜z＜h1时内孤立波诱导的水质点瞬时水平和垂向速度，而U2和W2分别为当-h2＜z＜ζ时内孤立波诱导的瞬时水平和垂向速度，则可得[18]：

图13 在Case B工况下，半潜平台无因次升力时历特性Fig.13 The time-variant characteristics for dimensionless lift forces for Case B

其中

由伯努利方程可得，内孤立波诱导的流体动压力为[19]

当ζ＜z＜h1时，定义；而当-h2＜z＜ζ时，定义对半潜平台立柱和横撑，将其统称为迎流柱型结构，利用Morison公式，由（7）式和（8）式可得，作用在单位长度的迎流柱型结构上的内孤立波载荷可表示为[20]：

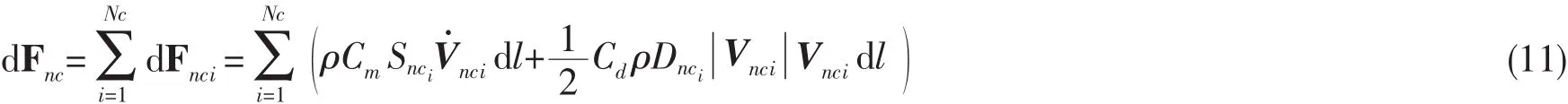
其中：Nc为迎流柱型结构的个数，Cm为惯性力系数，Cd为拖曳力系数，Snci为第i个迎流柱型结构的横截面积，Dnci为第i个迎流柱型结构的等效直径，和Vnci分别为水质点加速度和速度垂直于第i个迎流柱型结构表面的矢量分量。

设Umax为内孤立波诱导的最大水平速度，定义雷诺数数为为内孤立波特征周期，De称为半潜平台单位深度的等效直径）则根据文献[12]的系列实验结果，Morison公式（9）中的两个经验系数可表示为：

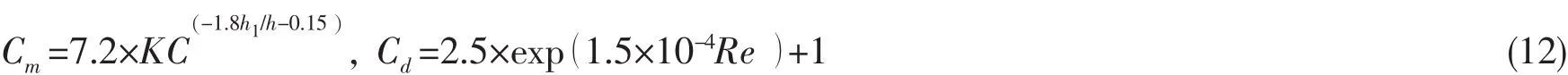
另一方面，内孤立波对半潜平台横撑上下表面及浮箱表面还会产生压差力载荷的作用，由（10）式可得，作用于半潜平台上的内孤立波压差力载荷为：其中：SB为半潜平台横撑上下表面积和浮箱表面积，nB为其表面单位法线矢量，方向指向横撑和浮箱结构的内部。

在内孤立波压差力载荷理论模型（13）式中，已经忽略了半潜平台对内孤立波特征的影响，因此（13）式也称为Froude-Krylov力。图14给出了Case B工况下，利用上述简化方法计算所得半潜平台内孤立波水平力、垂向力及其力矩幅值结果与CFD数值模拟结果的比较。由图可知，利用简化方法所得计算结果与CFD数值模拟结果吻合，两者之间的最大相对误差一般不超过13%。另一方面，由文献[12]可知，采用该简化方法的计算结果与实验结果也是吻合的，两者之间的最大相对误差一般不超过10%。由此可见，利用该简化方法计算半潜平台内孤立波载荷是可行的。

图14 内孤立波无因次水平力、垂向力及力矩幅值的理论与CFD数值模拟结果比较Fig.14 Amplitude results for dimensionless loads(horizontal forces,vertical forces,torques)due to internal solitary waves based on two methods

3 结 论

对有限水深两层流体，以N-S方程为控制方程，采用内孤立波在上下层流体中诱导的深度平均水平速度作为入口条件，建立了内孤立波与半潜平台强非线性作用的数值模拟方法。该方法对半潜平台内孤立波水平力、垂向力和力矩幅值及其时历变化特性的数值模拟结果与相应实验结果一致，可以用于内孤立波与海洋浮式结构强非线性作用的数值模拟。

研究表明，半潜平台内孤立波水平和垂向力由波浪压差力、粘性压差力和摩擦力组成。其中,水平摩擦力、垂向摩擦力均很小，可以忽略；水平力的主要成分为波浪压差力和粘性压差力，粘性压差力与波浪压差力相比较小却不可忽略，流体粘性的影响较小；垂向力中粘性压差力很小，流体粘性影响可以忽略。研究还表明，半潜平台对内孤立波的波形及其诱导流场的影响很小，垂向力可以采用傅汝德—克雷洛夫力公式进行计算，而水平力则可以结合Morison公式和傅汝德-克雷洛夫力公式进行计算。

[1]Helfrich K R,Melville W K.Long nonlinear internal waves[J].Ann.Rev.Fluid Mech.,2006,38:395-425.

[2]Choi W,Camassa R.Fully nonlinear internal waves in a two-fluid system[J].J Fluid Mech.,1999,396:1-36.

[3]黄文昊,尤云祥,王 旭,等.有限深两层流体中内孤立波造波实验及其理论模型[J].物理学报,2013,62(8):084705-084714. Huang Wenhao,You Yunxiang,Wang Xu,et al.Wave-making experiments and theoretical models for internal solitary waves in a two-layer fluid of finite depth[J].Acta Phys.Sin.,2013,62(8):084705-084719.

[4]陈景辉.南海流花11-1深海油田开发工程[J].中国海洋平台,1996,11(1):43-45. Chen Jinghui.Liuhua 11-1 deep sea oil-field development project in South China Sea[J].China Offshore Platform,1996, 11:43-45.

[5]Bole J B,Ebbesmeyer C C,Romea R D.Soliton currents in the South China Sea:Measurements and theoretical modeling [C]//The 16th Offshore Technology Conference in Houston.Texas,USA,1994:367-376.

[6]Cheng Y L,Li J C,Liu Y F.The induced flow field by internal solitary waves and its action on cylindrical piples in the stratified ocean[J].Recent Advances in Fluid Mechanics,Qinghua-Apringer,2004:296-299.

[7]Cai S Q,Long X M,Gan Z J.A method to estimate the forces exerted by internal solitons on cylinder piles[J].Ocean Engineering,2003,30(5):673-689.

[8]Cai S Q,Long X M,Wang S G.Force and torques exerted by internal solitions in shear flows on cylinder piles[J].Applied Ocean Research,2008,30(1):72-77.

[9]Xie J S,Jiang Y J,et al.Strongly nonlinear internal solution load on a small vertical circular cylinder in two-layer fluids[J]. Applied Mathematical Modelling,2010,34(8):2089-2101.

[10]尤云祥,李 巍,时忠民.海洋内孤立波中张力腿平台的水动力特性[J].上海交通大学学报,2010,44(1):12-17. You Yunxiang,Li Wei,Shi Zhongmin,et al.Hydrodynamic characteristics of tension leg platforms in ocean internal solitary waves[J].Journal of Shanghai Jiao Tong University,2010,44(1):56-61.

[11]尤云祥,李 巍,胡天群.内孤立波中半潜平台动力响应特性[J].海洋工程,2012,30(2):1-7. You Yunxiang,Li Wei,Hu Tianqun,et al.Dynamic responses of a semi-submersible platform in internal solitary waves[J]. Ocean Engineering,2012,30(2):1-7.

[12]黄文昊,尤云祥,石 强,等.半潜平台内孤立波载荷实验及其理论模型研究[J].水动力学研究与进展,2013,28(6): 644-657. Huang Wenhao,You Yunxiang,Shi Qiang,et al.The experiments of internal solitary wave loads and their theoretical model for a semi-submersible platform[J].Chinese Journal of Hydrodynamics,2013,28(6):644-657.

[13]关 晖,苏晓冰,田俊杰.分层流体中内孤立波数值造波方法及其应用[J].力学季刊,2011,32(2):218-223. Guan Hui,Su Xiaobing,Tian Junjie.Numerical method of solitary wave generation in a stratified flow and its applications [J].Chinese Quarterly of Mechanics,2011,32(2):218-223.

[14]高原雪,尤云祥,王 旭,等.基于MCC理论的内孤立波数值模拟[J].海洋工程,2012,30(4):29-35. Gao Yuanxue,You Yunxiang,Wang Xu,et al.Numerical simulation for the internal solitary wave based on MCC theory[J]. Ocean Engineering,2012,30(4):29-36.

[15]刘碧涛,李 巍,尤云祥,曲 衍,范 模.内孤立波与深海立管相互作用数值模拟[J].海洋工程,2011,29(4):1-7. Liu Bitao,Li Wei,You Yunxiang,et al.Numerical simulation of interaction of internal solitary waves with deep-sea risers [J].Ocean Engineering,2011,29(4):1-7.

[16]Hirt C W,Nichols B D.Volume of fluid(VOF)method for the dynamics of free boundaries[J].J Computational Physics, 1981,39(1):201-225．

[17]韩 鹏.基于VOF方法的不规则波阻尼消波研究[D].大连:大连理工大学,2008. Han Peng.The study of damping absorber for irregular waves based on VOF method[D].Dalian:Dalian University of Technology,2008.

[18]Camassa R,Choi W,Michallet H,Rusas P O,Sveen J K.On the realm of validity of strongly nonlinear asymptotic approximations for internal waves[J].J Fluid Mech.,2006,549:1-23.

[19]周光坰,严宗毅,许世雄,章克本.流体力学[M].北京:高等教育出版社,2003.

[20]董艳秋.深海采油平台波浪载荷及响应[M].天津:天津大学出版社,2005.

Numerical simulation for the load characteristics of internal solitary waves on the semi-submersible platform

WANG Xu1,LIN Zhong-yi2,YOU Yun-xiang1
(1 State Key Laboratory of Ocean Engineering,Shanghai Jiao Tong University,Shanghai 200240,China; 2 School of Jiaxing Nanyang Profession and Technology,Jiaxing 314003,China)

According to the applicability conditions for three type of internal solitary waves theories including KdV,eKdV and MCC,a numerical method based on the Navier-Stokes equation in a two-layer fluid is presented to simulate the strongly nonlinear interaction of internal solitary waves with a semi-submersible platform,where the velocity-inlet boundary is applied by using the depth-averaged velocities in the upperand lower-layer fluids induced by the internal solitary waves.The results show that the waveforms and amplitudes of the internal solitary waves based on the present numerical method are in good agreement with the experimental and theoretical results,and the numerical results for the horizontal and vertical forces,as well as torques on the semi-submersible platform due to the internal solitary waves have good agreement with experimental results.It is shown that the horizontal and vertical forces on the semi-submersible platform due to the internal solitary waves can be divided into three components which are the wave and viscous pressure forces,as well as the frictional force,where the frictional force is small and can be neglected. For the horizontal force,their main components are wave pressure and viscous pressure forces,where the viscous pressure force is small but can not be neglected.For the vertical force,the component of the viscouspressure force is small and can be neglected.Moreover,the effects of the semi-submersible platform on the waveforms and flow fields induced by the internal solitary waves are small,and it is shown that the loads on the semi-submersible platform due to internal solitary waves can be calculated by the Morison equation and Froude-Krylov force.

two-layer fluid;internal solitary wave;semi-submersible platform;load characteristics

P751

A

10.3969/j.issn.1007-7294.2015.10.002

1007-7294（2015）10-1173-13

2015-01-25

国家自然科学基金资助（11372184）；高等学校博士点基金资助（20110073130003）

王 旭（1985-），男，博士研究生；尤云祥（1963-），男，教授，博士生导师，通讯作者，E-mail:youyx@sjtu.edu.cn。