固体火箭发动机含裂纹药柱应力场有限元模拟的新方法①

任海峰，高 鸣

(海军航空工程学院， 烟台 264001)



固体火箭发动机含裂纹药柱应力场有限元模拟的新方法①

任海峰，高 鸣

(海军航空工程学院， 烟台 264001)

针对研究固体火箭发动机药柱出现裂纹前、后药柱内应力/应变场的需要，提出利用奇异单元和生死单元技术模拟含三维裂纹药柱的新方法，并利用该方法对固体火箭发动机三维非贯穿裂纹进行模拟，分析药柱裂纹附近区域应力分布的规律。结果表明，该方法便捷有效，尤其适用于对比研究裂纹、脱粘等药柱缺陷引起的应力释放和应力分布的变化。

固体火箭发动机；药柱；奇异单元；生死单元；裂纹

0 引言

固体火箭发动机在制造、运输、贮存和使用等过程可能产生裂纹、脱粘等典型药柱缺陷。发动机点火增压时，燃气压力、热量和振动等因素可能导致裂纹扩展，致使内弹道改变，甚至引发灾难性事故。因此，药柱完整性方面的研究是固体火箭发动机领域关注的重点问题之一[1]。但作为药柱主体的推进剂是以高聚物粘合剂为基体，并在粘合剂中填加固体氧化剂、金属燃烧剂和少量其他成分的多相混合物。材料本身的复杂性对裂纹的萌生和扩展产生的复杂影响很难描述[2-5]，一些裂纹开裂与止裂准则是随温度和时间变动的，试验测定环境与实际使用环境有较大差异[6]。发动机工作过程中裂纹的扩展过程还是一个复杂的热量-流体-结构耦合过程[7]。此外，断裂力学的相关理论如应力强度因子断裂准则、COD断裂准则、最大能量释放率准则和J积分准则等判断裂纹是否发生扩展仍需深入研究。利用有限元方法分析裂纹的萌生和扩展涉及预设裂纹扩展路径、重新划分化网格等操作，建模过程纷繁复杂[7]。因此，固体火箭发动机裂纹扩展机理复杂，现有裂纹模拟方法纷繁复杂，且效果欠佳。

固体火箭发动机实际服役过程中，往往只关心药柱是否存在裂纹，发生药柱裂纹缺陷的发动机一般直接判废或进行针对性的处理。近年随着固体仪器发动机技术的发展[8-9]，业界开始尝试使用传感器监测裂纹。该研究方向更多地关心裂纹产生、扩展对药柱应力场的影响，寻求粘接界面应力敏感点和缺陷特征点，并不关心裂纹萌生扩展等复杂过程。

本文以Abaqus软件为平台，研究利用奇异单元和生死单元技术模拟药柱有无三维裂纹情况下药柱应力场的新方法，并利用该方法对发动机三维非贯穿裂纹进行模拟，分析裂纹对发动机药柱应力分布的影响。此外，该方法同样适用于药柱脱粘的分析，也可利用J积分准则等裂纹断裂准则判断裂纹是否扩展，并预测裂纹扩展方向，具有较好的应用前景。

1 裂纹奇异单元和生死单元技术

1.1 裂纹奇异单元技术

按照断裂力学理论，裂纹尖端的应力、位移场可表示为[10-11]

(1)

(2)

式中σij(N)(i，j=1，2，3)为应力分量；ui(N)(i=1，2，3)为位移分量；N=Ⅰ～Ⅲ为裂纹类型；fij(N)、gij(N)(θ)为极角θ的函数。

图1 1/4节点二次等参奇异单元Fig.1 1/4 node isoparametric quadratic singular element

xA、xB、xC为A、B、C节点的坐标，uA、uB、uC分别为三节点的水平位移。

裂纹线上任意一点的坐标x和位移u都可用形函数插值：

x=-0.5η(1-η)xA+(1+η)(1-η)xB+0.5η(1+η)xC

u=-0.5η(1-η)uA+(1+η)(1-η)uB+0.5η(1+η)uC

-1≤η≤1

(3)

当xA=0，xB=L/4，xC=L，uA=0时，式(3)简化为

x=0.25(1+η)2L

u=(1+η)[(1-η)uB+0.5ηuC]

(4)

位移u对坐标进行微分：

(5)

在极坐标中x=r，θ=0，故式(5)可写为

(6)

当xB=L/2时：

x=0.5(1+η)L

u=(1+η)[(1-η)uB+0.5ηuC]

(7)

(8)

由式(8)可知，应力、应变不具有奇异性。因此，裂纹尖端采用1/4节点等参二次奇异单元可较好地实现应力、应变场的模拟。

1.2 生死单元技术

在模拟药柱是否存在裂纹时，本文采用了生死单元技术。有限元软件进行分析时，单元的“生死”是通过修改单元刚度的方式实现的[13]。单元被“杀死”时，单元并非将其从实际模型中删除，只是将其单元刚度矩阵乘上一个极小的缩减系数(该参数的缺省值为1.0×10-6，该参数取数值足够小即可，并非常量)，为了防止矩阵奇异，该参数不设置为0。与被“杀死”单元有关的单元载荷矢量(如应力、温度等)为0输出。对于“杀死”单元质量、阻尼和应力刚度矩阵设置为0。因为“杀死”的单元没有被删除，不包括在载荷列阵中，仍然可以通过列表显示它们。所以“杀死”前后刚度矩阵尺寸总是保持不变的，也就是说“杀死”前后模型单元一致，无须重构网络，这对求解分析带来极大便利。

单元的“激活”则是将被“杀死”的单元重新“激活”，在被“杀死”单元被重新“激活”时，其刚度、质量、单元载荷等均可以恢复至真实取值。但被重新“激活”的单元应变为0，若存在初应变，则可以通过实常数方式输入，并不受单元生死操作的影响。

2 数值模拟过程

以约束边界的推进剂方坯出现裂纹为例，利用奇异单元和生死单元技术模拟裂纹应力、应变场，涉及如下技术。

2.1 三维奇异裂纹单元建模

方坯裂纹尖端采用1/4节点等参二次奇异单元处理，如图2所示。本算例中Abaqus三维奇异单元建模分3步：

(1)用草图分割面，并指定扫略路径；

(2)采用扫略的方法分割部件；

(3)采用结构化和扫略2种策略划分模型网格，采用C3D8T单元，整体和局部网格如图2。

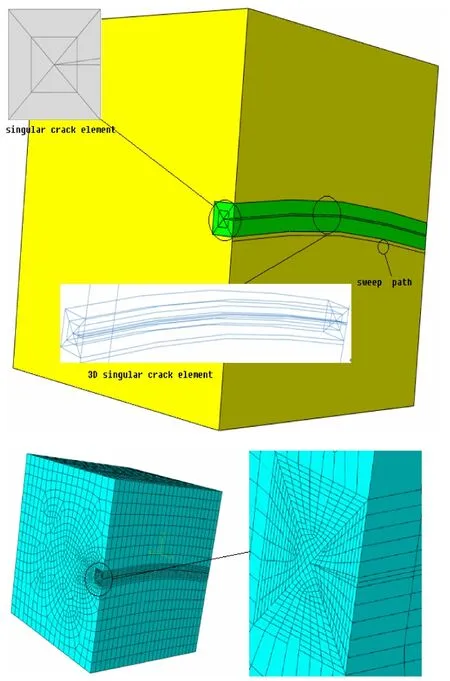
图2 奇异裂纹单元建模过程Fig.2 3D singular crack element modeling process with Abaqus

2.2 生死单元建模

生死单元建模过程如图3所示。在软件中建立分析步：Step→Create step→Step-2；Step-2：Dynamic，Implicit(用动态过程分析裂纹产生过程)，时间1 s，增量步0.000 1。二定义接触：在Interaction→Create interaction，选Step-2 ；如图3所示，选Model change→Continue，对话框，在视图中拾取裂纹，视图红色阴影部分，点选Deactivated in this step。

2.3 模拟结果

仿真结果如图4所示，裂纹尖端应力最大，截面的应力场分布模式符合I型裂纹尖端弹塑性区应力场分布特征。由于边界为固支边界，在粘接界面裂纹根部形成产生了应力集中，这与物理过程相符，方法简捷有效。

图3 生死单元建模过程Fig.3 Birth-death element modeling process with Abaqus

图4 三维曲线裂纹最大主应力云图Fig.4 Max principal stress of 3D curvilinear crack

3 发动机药柱三维非贯穿裂纹模拟

某试验用模拟发动机采用贴壁浇注的中心孔型药柱，外径150 mm，内径50 mm。降温固化引起的初始应力分布，可通过单元“生”状态下的有限元模拟获得其计算结果。此后，在中心孔轴向中点，人为设置长10 mm、深15 mm、宽0.5 mm的楔形裂纹，可通过单元“死”状态下的有限元模拟获得其计算结果。研究裂纹对药柱和包覆层粘接表面应力的分布的影响，以便为发动机裂纹监测系统及其传感器的设计布局优化提供参考。具体仿真过程在此不再详述，仿真结果如图5所示。

图5(a)给出了模拟发动机中心孔药三维非贯穿裂纹应力云图全景。如图5(b)所示，该方法很好的模拟了裂纹尖端应力场，裂纹尖端应力最大，完全符合I型裂纹尖端弹塑性区应力场分布特征，与文献[2，14]一致。如图5(a)、(c)所示，该方法模拟了非贯穿裂纹两端面应力集中情况，体现了结构对应力分布的影响,比如由于材料的破坏引起的应力集中,裂纹尖端两侧端面结构对应力应变的限制，以及靠近中心孔处裂纹应力的释放。

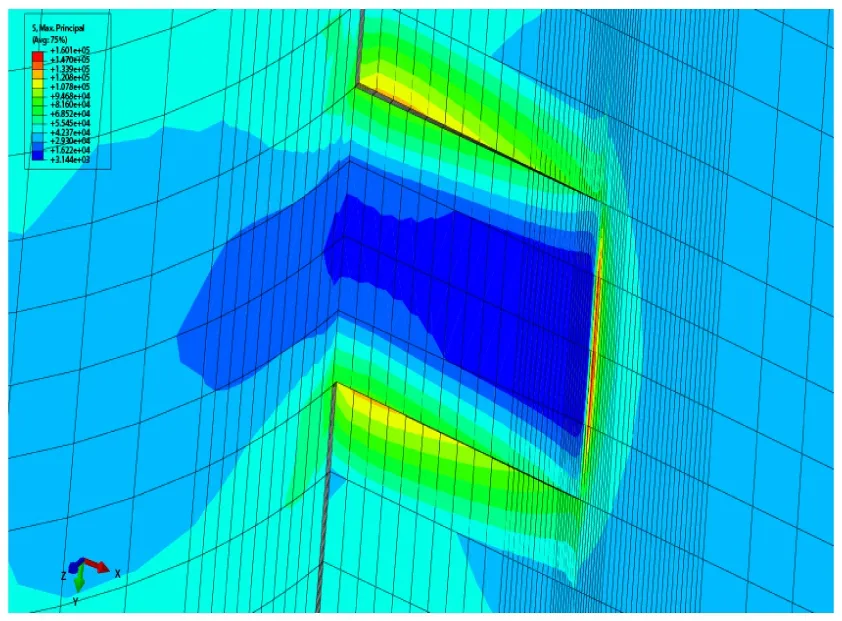
(a) 全景应力云图

(b) 截面应力云图

(c) 1/4截面应力云图

根据有限元的近似解性质[15]，应力和应变近似解一定在精确解上下震荡，但某些点上解正好和精确解相等，即最佳应力点。根据以应力为自变量的最小位能原理，采用高斯数值积分，由高斯积分的性质，可知积分点处应力的精度最高。因此，Abaqus中的应力存储在高斯积分点。一般来说，裂纹仿真都要重新划分裂纹网格，导致网格节点和单元的重新排列，需要将单元积分点应力向外插值到节点，获得节点应力，差值方法十分复杂。采用本文方法裂纹开裂前后无需重构网格，节点和单元一致，结果对比分析简单可靠。图6是模拟发动机粘接界面中点圆周方向最大主应力曲线，显示了中心孔裂纹对固体火箭发动机粘接界面应力分布的影响，对比分析不难看出裂纹开裂后，0°应力最大，40°～60°应力最小，180°应力恢复大约为未有裂纹的90%以上，与文献[16-17]一致。图7是裂纹产生前后粘接界面最大主应力分布相对变化着色面，着色面图代表应裂纹发生前后粘接界面应力的差值，该图非常直观地反映了粘接界面应力变化情况。裂纹引起的粘接界面应力相对于无裂纹状态的药柱粘接界面应力呈现出规律性和方向性变化。粘接界面应力变化整体保持在0 之下，较好地体现了中心孔裂纹引起的“附加位移”，产生的应力释放，导致药柱的整体“变软”，承载能力下降。裂纹尖端局部应力集中产生了应力激增，0°附近位置粘接界面应力局部激增达最大值。局部应力集中引起应力增加和整体应力释放的较量在0°～20°之间，应力集中占据上峰，在20°～30°左右达到平衡，在30°～60°之间附件位移产生的应力释放占据上峰，40°～60°粘接界面应力达到最小值，最大值与最小值之间差值为3 kPa。此后，应力集中和应力释放的影响随着远离裂纹逐渐衰减。由于裂纹的出现引起的应力存在以上的方向特征，因此发动机药柱缺陷的监测系统可以通过合理地选择和布置传感器监测裂纹的萌生并判断其位置。对于脱粘等其他会引起药柱内应力分布变化的缺陷，其分析方法和监测技术也同样有效。

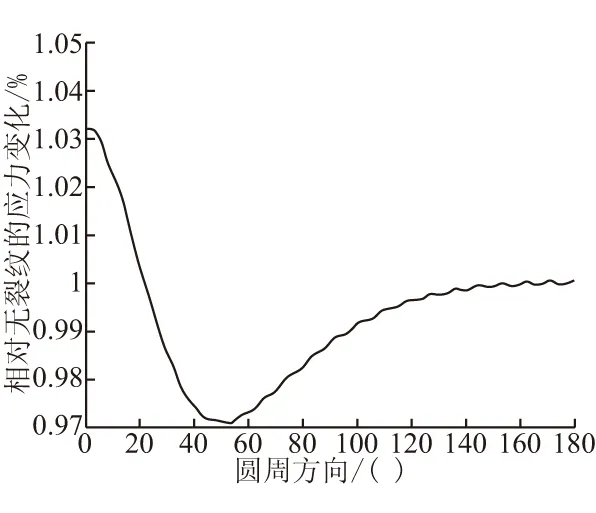
图6 模拟发动机粘接界面中点圆周方向最大主应力曲线Fig.6 Max main stress along circumferential direction by a bore crack of SRM

图7 裂纹产生前后模拟发动机粘接界面 应力分布相对变化着色图Fig.7 Relative bond stress 3D shaded surface and contour by a bore crack of SRM

4 结论

(1)基于奇异单元和生死单元技术的含三维裂纹药柱完整性模拟的技术，便捷有效，且可为结果对比分析提供了便利。

(2)裂纹的出现使药柱粘接界面应力分布呈一定的方向特性，使粘接界面应力监测系统的设计和优化成为可能。

(3)裂纹引起的药柱粘接界面应力变化幅值较小，监(检)测有一定难度，要求监测传感器具有很高的灵敏度和稳定性，或采取降温等措施使应力变化幅值增大。

[1] 胡松启，周宴星，刘迎吉,等.固体推进剂裂纹扩展研究综述[J].火箭推进，2012，38 (5):86-92.

[2] 刘著卿,颜世东,丁彪. 药柱裂纹对固体火箭发动机工作过程的影响[J]. 海军航空工程学院学报,2007,22(4): 443-446.

[3] 刘承武，阳建红，邓凯,等.基于Mori-Tanaka 有限元法的粘弹复合推进剂非线性界面脱粘[J]. 推进技术,2011,32(2):225-229.

[4] Bencher C D． Microstructural damage and fracture processes in a composite solid rocket propellant[J]． Journal of Spacecraft and Rockets，1995，32(2):328-334.

[5] 曾甲牙．丁羟推进剂拉伸断裂行为的扫描电镜研究[J].固体火箭技术，1999，22(4):69-72.

[6] 彭威，周建平，赵维昌，等． 复合固体推进剂应力分布的数值模拟及损伤萌生分[J]. 固体火箭技术，2002，25(1):12-15.

[7] Dick W A,Health M T,Fiedler R A. Integrated 3-D simulation of solid propellant rockets[R]. AIAA 2001-3949.

[8] 高鸣,任海峰.固体仪器发动机健康检测技术评述与研究[J].固体火箭技术，2013,36 (2)：278-284.

[9] 高鸣,任海峰. 固体仪器发动机粘接界面应力监测系统设计[J].火炸药学报，2013,36 (4)：69-73.

[10] Rice J R,Rosengren G F. Plane strain deformation near crack tip in a power law hardening material [J].Journal of Mechanics and Physics of Solids,1968,16(1):1-12.

[11] 唐立强,谭英杰,蔡艳红. 刚性-粘弹性材料界面I 型动态扩展裂纹的尖端场[J].力学季刊，2004,25(2):188-194.

[12] Homas J R Hughes,Akin J E.Techniques for developing special finite shape function with particular reference to singularities[J]. International Journal for Numerical Methods in Engineering，1980，15：733-751.

[13] ABAQUS Inc. ABAQUS Analysis User's Manual/6.12.1 ABAQUS/Aqua analysis [K].2010.

[14] 徐学文，孙建国，牟俊林. 某固体火箭发动机药柱上三维裂纹扩展的判定[J].固体火箭技术，2008，31(4)：331-335.

[15] 王勖成. 有限单元法[M].北京：清华大学出版社，2003.

[16] Tussiwand G,et al. Application of embedded sensor technology to a full-scale experimental nozzleless rocket motor[R].AIAA 2007-5790.

[17] Reeling Brouwer G,et al. Evaluation of ageing in composite propellant grains part 2[R].AIAA 2005-3803.

(编辑：吕耀辉)

A new simulation method of 3D crack of solid rocket motor grain

REN Hai-feng，GAO Ming

(Naval Aeronautical and Astronautical University，Yantai 264001,China)

To study the variations in stress/strain field when the crack appears,a new technique to simulate 3D crack of solid rocket motor grain based on singular element and birth-death element was proposed. A part-through crack for solid rocket motor grain simulated by utilizing this method and stress distribution caused by crack were analyzed. Simulation results indicate that the method is correct,effective,and convenient for further research,especially suitable for comparative analysis on the stress distribution changes and the stress reliefs which are caused by crack or debond.

solid rocket motor；grain；singular element;birth-death element;crack

2014-11-06；

：2014-12-01。

国防预研项目(51328050101)。

任海峰(1978—)，男，博士，研究方向为火箭发动机健康监测技术。E-mail:haifeng_ren@163.com

高鸣(1957—)，男，博士，博士生导师,研究方向为火箭发动机技术。

V438

A

1006-2793(2015)01-0050-05

10.7673/j.issn.1006-2793.2015.01.09