贝雷法在路面施工质量控制中的应用
2015-04-24张燕清
■张燕清
(三明市交通建设投资有限公司,三明 365000)
我国目前沥青路面配合比设计过程中,级配选定主要按照施工设计图与你施工规范要求的范围选定, 因此,设计过程中要求设计人员具有一定工作经验,才能设计出一条合理并具有实施性的级配线,同时,级配的选定过程中具有很强的主观性。在我国近20 年高速公路大建设过程中, 随着社会经济不断发展, 交通量猛增,造成早期路面损害较为严重,我们在病害的原因分析过程中,发现有不少因级配设计不合理所造成。本文主要通过介绍贝雷法及贝雷参数在湄渝高速公路三明段ATB-25 柔性基层配合比级配检验分析与施工过程中对质量控制应用,通过项目检验取得很好效果。
1 贝雷法级配检验分析
“贝雷法” 级配设计法是美国伊利诺州交通局Robert D.Bailey 研究的一套系统的设计和检验沥青混合料级配的方法,称为嵌挤密实结构级配设计法,适用于多类沥青混合料配合比设计,可与Superpave 方法、马歇尔设计法等结合使用。在我国与马歇尔设计法配合使用,能够设计出良好的嵌挤结构,进一步提高沥青混合料的高温稳定性与耐久性。
贝雷法主要特征是通过控制粗细集料关键筛孔尺寸的通过率比例关系,让矿料级配获得良好的骨架结构。利用平面圆作为数学模型,以干涉理论作为理论设计依据,考虑不同集料性状组合和组合后的空隙。粗颗粒间空隙尺寸的大小取决于颗粒形状和尺寸,如图1 所示。当颗粒全为圆形时如图1(a), 空隙尺寸为颗粒直径d的0.15 倍,即0.15d;当组成颗粒中有两个圆面和一个平面时,如图1(b),空隙尺寸为0.22d;当一个圆面和两个平面的颗粒组合时,如图1(c),空隙尺寸为0.24d;当颗粒全为平面时,如图1(d) ,则空隙尺寸为0.28d。系数0.22 是这4 种情形的平均值。 将最大公称粒径(NMPS)尺寸0.22 倍对应的标准筛网尺寸作为级配粗细集料的分界点,比其尺寸大的集料为粗集料,反之为细集料,并将与计算值最靠近的标准筛孔尺寸当作组成集料的第一控制筛孔(PCS)。细集料亦依照该原理划分为细集料里的粗集料以及细集料里的细集料,且产生依次的填充状态, 作为第二控制筛孔 (SCS),SCS=PCS×0.22,第三控制筛孔(TCS)则是TCS=SCS×0.22。合成级配比例确定之后, 贝雷法提出3 个参数对其展开分析,分别为:矿料中粗集料比(CA),矿料中细集料的粗料比(FAc)及矿料中细集料的细料比(FAf)。
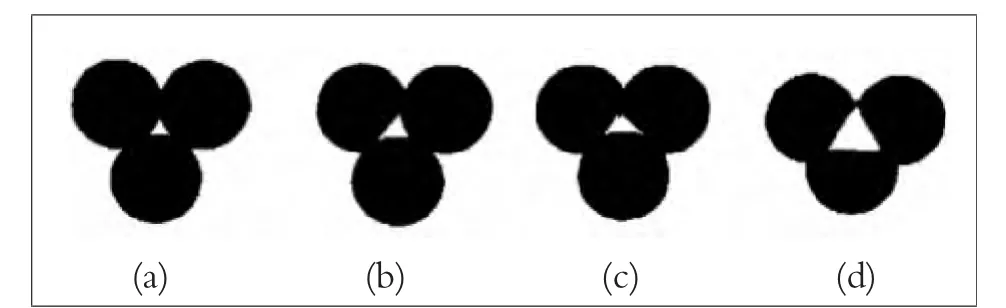
图1 颗粒形状组合和空隙
(1)CA 比,用于评价矿料中粗集料的含量和分析空隙特征。
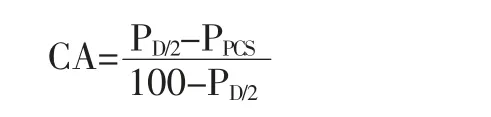
式中:PD/2是粒径等于D/2(D 是公称最大粒径)的通过率,%;PPCS为第一控制筛孔的通过率,%。
我国在使用贝雷法展开级配设计的时候,大体均是应用CA 来检验挑选的级配,认为在CA 处于0.4~0.8的区间范围时,粗集料可以出现嵌挤或是骨架。以ATB-25 沥青碎石混合料为例,如果CA 较小,通常低于0.4 时,沥青混合料非常易于出现离析, 而伴随CA增长,沥青混合料则愈加难以压实。当CA 趋近于1.0时,粗集料里的任一部分均无法构成粗集料骨架。虽然此类混合料很难离析,但因其包括许多干涉料,导致粗集料部分没办法获得较好填充,而且沥青混合料很难压实,出现推挤的可能性较大。当CA 比高于1.0 时,粗集料里的细料部分对于粗集料骨架的构成具有主导性效用,粗料部分开始作为填塞料,导致粗集料骨架的间隙封闭。因此考虑最佳压实特性的CA 范围是0.4~0.6 间。
(2)FAc, 反映细集料中粗料部分与细料部分的嵌挤、填充情况,计算公式为:
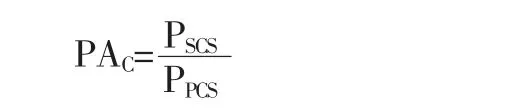
式中:PSCS为第二控制筛孔的通过率,%。
FAc变大,细料成分占比变大让细集料变成更密集的结构。 可是比值大, 说明细料太多, 在0.45 次级配图里就有 “驼峰” 曲线形成。 产生以下不良后果:1)减少混合料的强度与抵御永久变形的能力;2) 集料VMA 不合格,不能确保足够的沥青膜厚;3)混合料对沥青比例很敏锐, 沥青的细小变化均会让混合料变得十分不稳定;4)有可能导致压实不稳定, 形成重大的推移、开裂。假如FAc比值低,细集料里的粗料空隙用很少的细料填充,则会提升VAM 与混合料的空隙率。在0.45 次方级配图里曲线会出现凹状, 会形成难压实状况。 在3 个参数里FAc值对混合料VAM 作用最明显。 通过以上可知细集料构成非常重要, 在级配设计时, 不可以只是采取0~5mm 的一种规格材料, 通常0.3~2.36mm 之间的材料无法符合级配规定, 粉尘又多让比值太大亦或太小,导致不良级配,对混合料的施工特性与路用性能产生不好作用。 以ATB-25 沥青碎石混合料设计为例,提议FAc控制在0.4~0.6 间。
(3)FAf比体现了合成集料中最细一级的嵌挤状况,计算公式为:
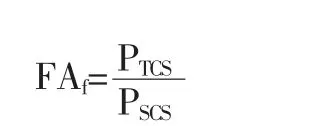
式中:PTCS为第三控制筛孔的通过率,%。
细集料中的FAf能够评价细集料中的细料成分的填充特性。 和FAc一样, 其值影响混合料的体积特性。FAf增加混合料的空隙减少;FAf减小VMA 值增大。以ATb-25 沥青碎石混合料为例,建议ATB-25 的FAf在范围0.4~0.6 间。
2 贝雷参数在配合比设计中的应用
以三明湄渝高速公路莘口-明溪路面B1 合同段ATB-25 沥青碎石,密级配混合料为例,粗细集料分档分别为(19-26.5)mm: (9.5-19)mm: (4.75-9.5)mm:(0-4.75)mm: 矿粉=23.5%:32%:12%:31.5%:1%,如表1 所示。
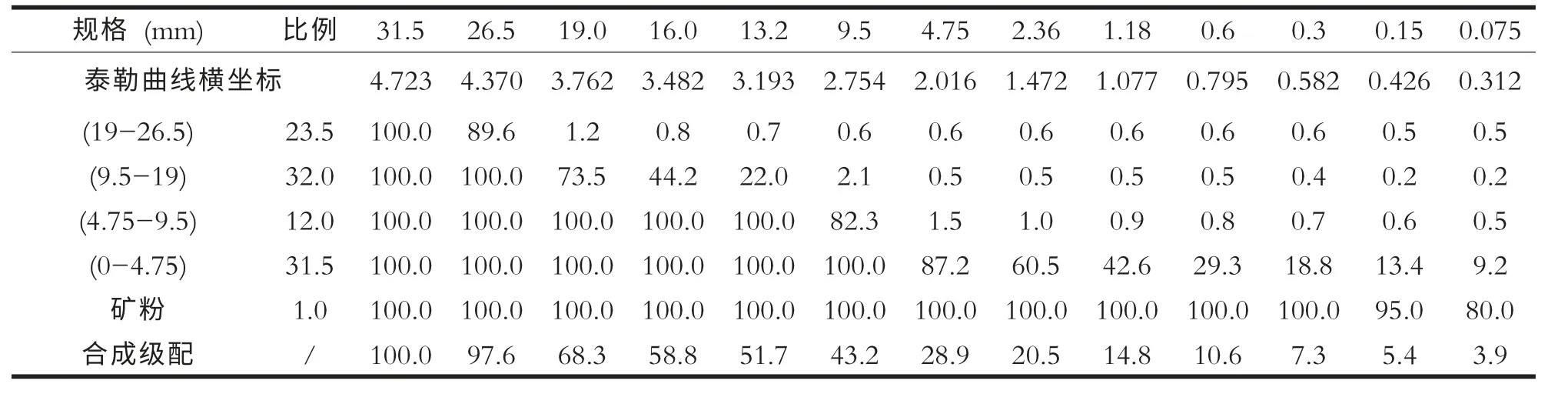
表1 ATB-25 级配设计表

图2 级配泰勒曲线图
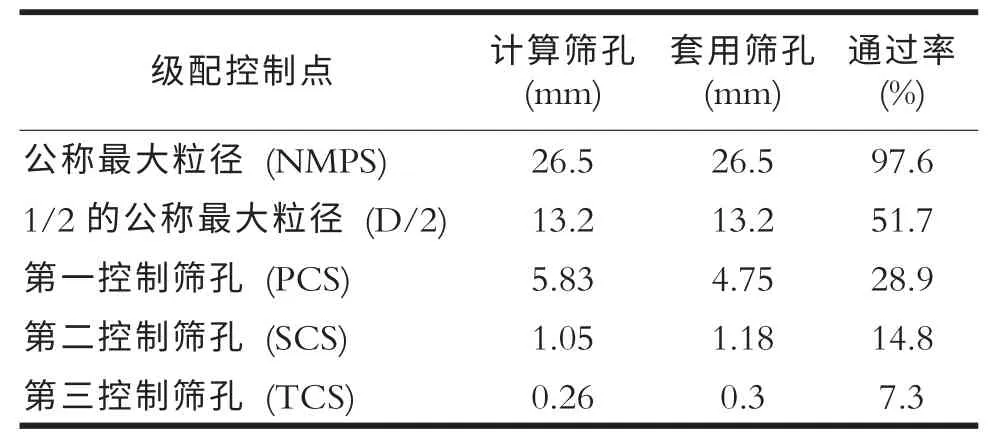
表2 ATB-25 级配控制点汇总
因为贝雷法对集料颗粒假设是近似圆或立方体,认为直径d 从0.15~0.28 均不会对级配形成影响,因此为了使选用的PCS 控制计算筛孔与级配中的固定筛孔一致,可以套用近似筛孔如表2。
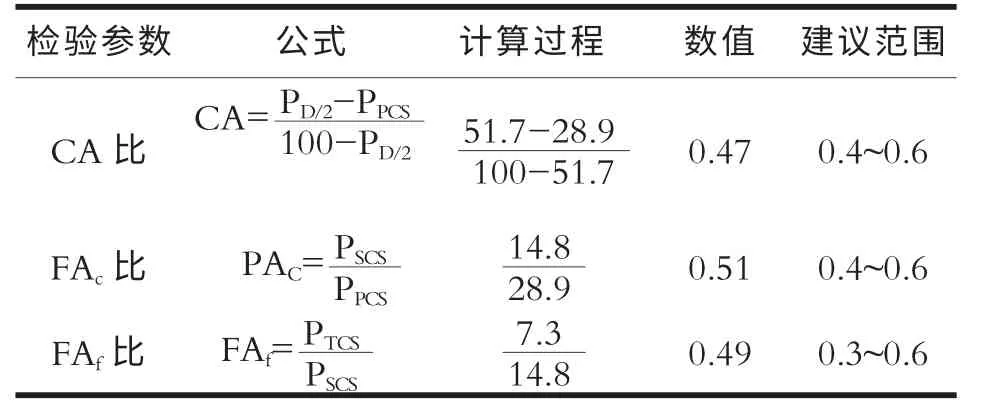
表3 检验参数计算
笔者通过骨架接触度 (SSC,stone-on-stone contact) 对级配进行评价。 根据美国NCHRP 第386 号项目的研究成果, 沥青混合料的级配优选可以采用混合料中的集料嵌挤状况来进行评估:当骨架接触度SSC>90%时,混合料是紧排骨架密实结构;骨架接触度SSC在85%~90%之间时, 混合料是松排骨架密实结构骨架接触度SSC≤85%时,混合料是悬浮密实结构。 如表4计算得SSC=91.8%,该级配属于紧排骨架密实结构。

表4 SSC 计算评估
应用体积法预估最佳沥青用量,根据沥青设计比设计方法, 最终选定ATB-25 的最佳沥青用量为3.8%,并进行混合料路用性能检测, 结果显示: 残留强度比(%):90.3>75; 旋转压实反算125 次压实空隙率:5.4。同时在配合比验证阶段的试验路试辅中,现场混合合料均匀整体无离析, 压实度与芯样空隙率均满足设计要求,以上指标均验证该级配具有良好高温稳定性与施工和易性。
3 贝雷参数在施工过程中的动态管理
在高速公路的项目管理过程中应用SPSS 软件提供的数值统计分析功能可以对一些质量指标进行统计分析,有效提高数据统计分析的工作效率与精确度,为工程质量管理提供科学依据。本文通过例举三明湄渝高速公路莘口-明溪路面B1 合同段ATB-25 上基层施工,施工管理过程中对沥青混合料级配的贝雷参数进行动态跟踪与分析,判断混合料级配的稳定性。采集数值见表5。

表5 施工贝雷参数采集表
采用质量控制图, 个体与移动全距的办法, 对CA、FAc、FAf进行动态跟踪, 主要参数(主要为:①在±3σ 范围;②正负中线8 个百分点;③最后3 项中的2 项±2σ) 进行范围监控, 并设置CA 范围上限:0.6,下限:0.4,目标值为设计级配CA 值:0.47。FAc与FAf同理设置。
图3 对CA 进行动态跟踪, 其中控制中心线为0.484;控制上限线(UCL)=μ+3σ=0.604;控制下限线(LCL)=μ-3σ=0.364。 动态走势图对3 月21 日指标进行红色报警,虽然,该日CA=0.587 在CA 范围内(CA设置范围值:0.4~0.6),但超出范围监控第③项(最后3项中的2 项±2σ), 我们应通过结合其他指标与现场施工情况分析原因。
图4 分析出CA 在整体生产过程中处于稳定状态,各项指标均正常,其中控制中心线为0.536;控制上限线(UCL)=μ+3σ=0.660;控制下限线(LCL)=μ-3σ=0.412,容量指标见表6。

表6 处理统计量
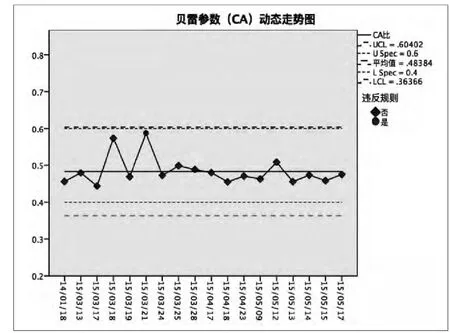
图3 CA 动态走势图

图4 FAf 动态走势图
4 贝雷参数与VMA 建立模型
贝雷参数在沥青混合料中的应用,可以使配合比设计中对级配的选定有更深了解, 从而更好的优化级配线。同时,矿料间隙率(VMA)在沥青混合料体积参数指标中非常重要,我们可以通过贝雷参数与VMA 建立模型,推导出经验公式,能够服务工程项目,积累工程经验与提高工程管理水平。
笔者以ATB-25 柔性基层施工的前9 个工作日的矿料间隙率(VMA)实测指标(见表7),采用非线性回归分析进行模型拟合,VMA 为因变量, 模型公式:VMA =a+b×FAC+_c×CA×CA+d×FAc×FAc+e×FAf×FAf+f×CA×FAc+g×CA×FAf+h×FAc×FAf, 采用列文伯格-马夸尔特法(Levenverg-Marquardt),设置平方和收敛性和参数收敛性为1e-8,计算出迭代数为5.1 时连续残差平方和之间的相对减少量(SSCON)最多为1E-8时停止运算,如表8 所示。

表7 马歇尔试验VMA 结果
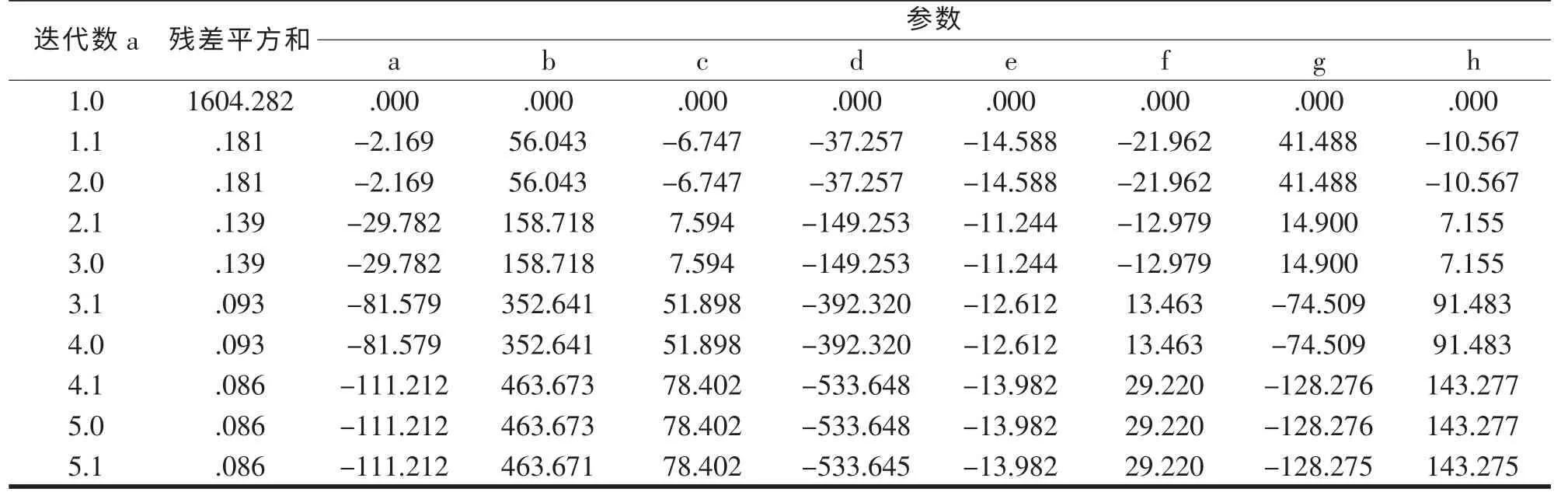
表8 迭代历史记录b
通过参数评估值可以分析模型影响显著的变量有d、b 和h,分别为FAf、CA、CA×FAc,而影响相对不显著的变量有e,f 分别为CA×CA 和FAc×FAc(见表10 未调整前参数估计值表),模型的拟合优度检验结果显示R2 为0.846, 使用德宾-沃森统计量 (Durbin-Watson) 检验残差是否存在自相关, 其取值范围介于0~4 之间,其值越接近2,说明变量之间是相互不依存的,本文拟合优度检验结果为1.605,可以基本确定残差是不依存的。

表9 未调整前参数估计值表

表10 Durbin-Watson 检验
笔者决定取消e、f 变量, 重新建模, 调整模型公式为VMA=a+b×FAc+c×CA×CA+d×FAc×FAc+g×CA×FAc+h×FAc×FAc。拟合优度检验结果显示R2 为0.822,拟合优度检验结果Durbin-Watson 为1.605。

表11 调整后参数估计值表
通过线性回归置性区间采用95%水平值进行方差分析(Anova),回归模型F 值为32.351,显著性(Sig.) 值为0.001<0.05, 可以判断采用的这个回归模型是有统计学意义的,系数检验值(见表12)。
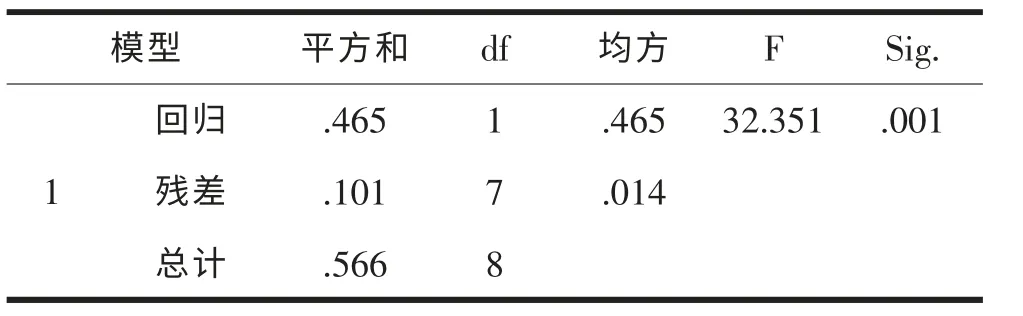
表12 Anova 检验表
最终得出回归方程:VMA=-93.935+397.918FAc+52.759CA2-409.426FAc2-62.117CA×FAf+54.764FAc×FAf。

表13 实测VMA 与预测VMA 对比表
我们对矿料间隙率(VMA)-贝雷参数回归方程进行验证数据(见表13), 前9 个工作日为回归数据值,后9 个工作日为验证值, 并采用独立样本T 检验, 置信区间设置为95%, 分析判断18 个工作日的VMA 预测值与VMA 实际值两个不同总体均值之间的差异性进行检验, 分析结果 (见表15, 表16) 为显著值为0.974>0.05, 所有确定两总体均值之间不存在显著差异, 也就是回归方程在湄渝高速公路ATB-25 施工中具有指导意义。
表14 组统计量
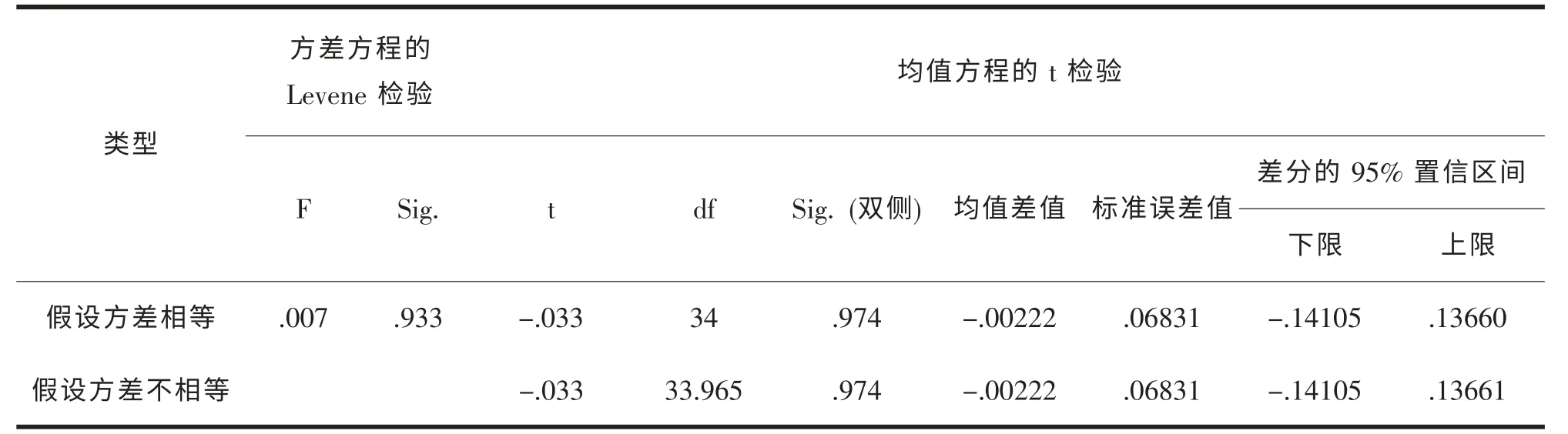
表15 独立样本检验
5 结论
(1) 贝雷法使广大建设者在优化级配中,从单一的0.45 次方级配曲线试配的经验法中解放出来, 通过贝雷法三参数可以更系统的评价混合料级配骨架嵌挤的情况。以保证混合料优良的体积特性(合适的VMA和空隙率) 和施工性能 (良好的压实性能和施工和易性),从而使设计出来的混合料达到骨架密实,兼具良好的高温抗车辙能力和耐久性。
(2) 应用SSC(stone-on-stone contact) 骨架接触度对贝雷法设计的级配进行评价。
(3)项目管理过程中应用统计软件在生产过程中对贝雷参数进行动态跟踪与分析,有效提高统计分析的工作效率与精确度,为工程质量管理提供科学依据。
(4)建立贝雷参数-VMA 回归方程,项目管理人员可以在已知级配通过率情况下, 预测VMA 值是否合格, 同时可以验证和反算马歇尔试验体积参数是否正常,为工程管理多一种管理手段与思路。
参与文献
[1]William R V ,William J P,Samuel H C.Bailey method for gradation selection in HMA mixture design[R]Transportation Research Circular Number E-C044,2002.
[2]曹卫东,吕伟民,李晓军.集料级配评估的贝雷法.1671-2579.
[3]《spss 统计分析》时立文著,清华大学出版社.
[4]谢志华.谈谈Durbin-Watson 检验[J].预测,1987,(06).
