多变量调节固冲发动机动力学建模及仿真

邵明玉，王志刚

(西北工业大学 航天学院，西安 710072)



多变量调节固冲发动机动力学建模及仿真

邵明玉，王志刚

(西北工业大学 航天学院，西安 710072)

分别建立了多变量调节固冲发动机各部件的性能/平衡模型、动力学模型以及扰动传播模型，并综合为多变量调节固冲发动机动力学模型。在此基础上，对飞行条件扰动以及进气道/燃气发生器/喷管调节时，发动机的响应特性进行了仿真分析，并分析了扰动的传播过程及不同扰动传播过程处理方法对发动机响应的影响。结果表明，进气道调节不会改变推力和补燃室压强的稳态值，燃气流量调节对推力有较大影响，喷管调节对补燃室压强有较大影响。

固冲发动机；多变量调节；动力学建模

0 引言

固冲发动机因其全固体、整体式设计，而具有结构紧凑、有利于小型化、使用维护简单等优点，被认为是中等超声速、中远程、小型战术导弹的理想动力装置[1]。为保证这些优点，现行固冲发动机多采用折中设计方案，即普遍采用固定几何简单结构方案，进气道和喷管的内流道结构按照低速接力要求设计，以保证低速正常接力[1-3]。高速巡航飞行时，进气道对来流压缩不足，喷管流通能力过大，膨胀做功能力不足，致使冲压发动机热力循环不完善，推力损失过大，背离其作为战术导弹高速巡航动力装置的设计初衷[1-3]。

从本质上讲，为适应宽马赫数工作范围，固冲发动机理应连续调节，方可充分发挥其应有的高速巡航性能优势。因此，有学者提出了多变量调节固冲发动机的概念，即从源头上依托进气道调节技术，在全设计速度范围内提升进气道总压恢复系数；在出口处，依托喷管调节技术，节制喷管流量，有效调节补燃室工作压强，提升喷管膨胀做功能力；在中间环节恰当控制燃气发生器的燃气流量，提升冲压发动机的推力性能[1]。

在多变量调节固冲发动机的概念中，进气道/燃气发生器/喷管根据飞行条件和推力指令进行调节，为了使发动机在稳定工作的同时实现性能最佳，并满足推力指令的要求，必须对进气道/燃气发生器/喷管的调节进行有效的控制。简单、精确的动力学模型是深入理解固冲发动机在飞行条件扰动和进气道/燃气发生器/喷管调节下响应特性，并进行多变量调节控制系统设计的基础。

针对固冲发动机的动力学建模问题，Herbert[4]以及NIU Wen-yu[5-6]分别采用集总参数法，建立了冲压发动机及燃气流量可调的固冲发动机的线性动力学模型；刘华[7]和钱柏顺[8]分别基于Willion方法[9-10]，建立了冲压发动机的线性动力学模型；Nitin K Gupta等[11-14]则建立了燃气流量及喷管可调的冲压发动机的非线性动力学模型，并对发动机的响应特性进行了分析。但这些模型大多只针对某一特定的扰动或调节，而且其中考虑的固冲发动机动力学环节有限。

本文针对多变量调节固冲发动机的主要部件，分别建立进气道、燃气发生器、补燃室及冲压喷管的流动性能/平衡模型、动力学模型及扰动传播模型，并将这些模型综合在一起，形成多变量调节固冲发动机动力学模型。在此基础上，对飞行条件扰动及进气道/燃气发生器/喷管调节下，发动机主要参数的响应特性进行仿真分析，并分析扰动传播的动态过程及扰动传播的处理方法对发动机响应特性的影响。

1 动力学建模

典型的固冲发动机由进气道、燃气发生器、补燃室及喷管组成，其结构简图及各特征截面的定义如图1所示。0～2表示进气道，其中1为进气道外罩唇口，t为进气道喉道出口，s为结尾正激波，u和d分别为正激波上游和下游；3～4表示补燃室；4～6表示冲压喷管，其中5为喷管喉道；g与gt分别为燃气发生器和燃气发生器喷管喉道。

多变量调节固冲发动机动力建模问题复杂，各部件的模型包括性能/平衡模型、动力学模型及扰动传播模型等。结合各部件具体特点，分别进行建模，并综合为多变量调节固冲发动机动力学模型。

图1 固冲发动机结构简图及特征截面Fig.1 Sketch of ducted rocket with station number

1.1 性能/平衡模型

性能/平衡模型描述的是各部件内部的流动守恒关系及相关性能计算。针对发动机各部件分别建模。

1.1.1 进气道

超声速进气道由超声速扩压段、喉道段及亚声速扩压段组成。

(1)超声速扩压段

超声速扩压段和喉道段决定了进气道所保有的最佳性能， 正常工作时，喉道出口参数由上游条件决定。因此，此段模型根据飞行条件和进气道结构参数，计算喉道出口参数。

对于可调进气道，楔板折角可调节，进气道始终工作在设计状态或其附近，流道内波系结构完整，喉道出口参数可直接根据激波系理论近似计算，或通过CFD计算结果插值得到。喉道出口参数可表示为

(1)

式中δ、x1、ht分别为进气道楔板折角、唇口位置和喉道高度。

(2)亚声速扩压段

亚声速扩压段被结尾正激波分成超声速流动段和亚声速流动段两部分。假设超声速流动段为绝能等熵流动，亚声速流动段为绝能流动，并用σsub集中体现亚声速扩压段的流动损失。则超声速流动段及亚声速流动段两端气流稳态参数之间的关系，可根据一维定常管流关系进行计算。

1.1.2 补燃室

采用零维模型计算二次燃气参数。补燃室出口流量等于流经喷管喉道的流量，即

(2)

用σab表示补燃室的总压恢复系数，则补燃室的出口总压可写为

(3)

其中，σab根据工程经验取值。二次燃气的总温根据热化学平衡理论计算，燃烧的理想温升可表示为燃气-空气比的函数：

(4)

考虑火焰传播、燃烧不充分等原因造成燃烧效率问题，二次燃气总温可表示为

(5)

式中nc为燃烧效率。

1.1.3 冲压喷管

冲压喷管完成气流的膨胀做功过程，并调节补燃室压强。一般来说，喷管中压力比足够大，喉道处足以形成壅塞流动，其质量流量可写为

(6)

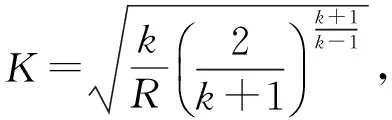
冲压喷管由收缩段和扩张段组成，假设喷管收缩段流动为绝能流动，并引入喷管效率nN集中体现喷管流动中的总压损失[15]；扩张段流动为绝能等熵流动，则收缩段和扩张段两端气流参数之间的关系，可根据一维定常管流进行计算，最终得到喷管出口参数。

1.1.4 推力计算

采用名义推力来分析发动机的工作状态对发动机推力的影响。发动机的名义推力定义为出口冲量减去入口冲量[16]，即

(7)

式中π(M)为气动函数，表示静压与总压之比。

1.2 动力学模型

动力学模型描述的固冲发动机中的各个动力学过程。固冲发动机的动力学过程呈现多学科性，包括流体动力学、热力学领域的多种物理现象。分别针对结尾正激波、燃气发生器及补燃室的动力学过程，建立动力学模型。

1.2.1 结尾正激波

稳态激波上游或下游发生扰动时，激波的传播速度将会发生改变，激波在管道中的运动速度为

(8)

激波下游的流量和总温根据质量守恒定律及能量守恒定律求得：

(9)

(10)

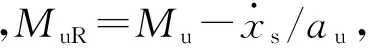
(11)

1.2.2 燃气发生器

燃气发生器通过调节喷管喉道面积控制燃烧室压强，调节燃气生成率以及排出的燃气流量。根据质量守恒方程，燃烧室内生成的燃气流量与喷管排出的燃气流量之差等于燃烧室内燃气质量随时间变化率[16-17]。

(12)

根据经典的固体火箭发动机燃烧室动力学模型[16-17]，可将式(12)整理为如下形式：

(13)

式中ρp为贫氧推进剂密度；a为推进剂燃速系数；n为推进剂压强指数；C*为推进剂特征速度。

燃气发生器排出的燃气流量为

(14)

1.2.3 补燃室

补燃室中包括流体动力学、热动力学等领域的物理现象，建模中一般考虑温度动力学和压力动力学，分别表示其能量存储效应和质量存储效应[18]。固冲发动机中，燃气热力学状态的改变由富燃燃气与空气掺混燃烧引起，温度变化速度快，且补燃室容积小，动态过程可忽略。因此，在补燃室动力学建模中，只考虑压力动力学。

选取结尾正激波到冲压喷管喉道之间的区域作为控制容积，并以进气道出口为界限，将其划分为冷区和热区。冷区定义为从结尾正激波到进气道出口之间的区域；热区定义为从进气道出口、燃气发生器喷管喉道到冲压喷管喉道之间的区域。

忽略燃气发生器调节及喷管调节引起的热区容积的变化，则以冷区和热区作为控制容积的质量守恒方程可写为

(15)

假设冷区与热区的流动均为等熵流动，冷区和热区的密度变化可表示为

(16)

(17)

冷区容积变化由结尾正激波运动引起：

(18)

将以上公式及理想气体状态方程代入质量守恒方程中，可解得补燃室压强的变化率为

(19)

其中

1.3 扰动传播模型

扰动传播模型描述的是扰动传播的动力学过程，固冲发动机中，扰动以声波和熵波的形式向上游和下游传播[8-9,19]。在面向控制的动力学建模中，这样的方法过于复杂，学者们对扰动传播过程多采用简化处理方法。

1.3.1 扰动传播处理方法

针对扰动传播动态过程的简化，学者们提出了2种方法，即分别近似为惯性环节和延迟环节。

用y表示变量，yss表示变量的稳态值，τ表示时间常数，采用惯性环节近似扰动传播过程时，参数响应可表示为

(20)

采用延迟环节近似扰动传播过程时，参数响应可表示为

y(t)=yss(t-τ)

(21)

1.3.2 扰动传播时间

在计算扰动传播时间时，将变量的扰动分为2种，声学变量的扰动和非声学变量的扰动[10-13]。

非声学变量的扰动随流动向下游传播，传播速度与气流速度相同，扰动传播的时间常数为

(22)

式中i、j为站点位置；u(x)为轴向位置x处的流动速度。

声学变量，即压力的扰动通过声波向上游或下游传播，相对主流的传播速度为声速，扰动传播时间常数为

(23)

式中a(x)为位置x处的声速，正号与负号分别表示扰动向下游或上游传播。

1.4 模型综合

将各部件的性能/平衡模型、动力学模型及扰动传播模型，按照部件在固冲发动机中的位置关系组合到一起，构成多变量调节固冲发动机非线性动力学模型，模型结构及各子模型间的参数传递关系如图2所示。

2 开环仿真

基于上述多变量调节固冲发动机动力学模型，对发动机受到扰动时，各参数的变化规律进行仿真，分析发动机响应特性。

2.1 典型飞行状态

固冲发动机本质上为高速巡航飞行而设计，故选取巡航状态作为典型飞行状态进行开环仿真。巡航飞行条件为

M0=3.5,H=15 km,α=0°

稳态条件下，进气道/燃气发生器/喷管以及发动机相关参数的初值见表1。

2.2 响应分析

对飞行条件扰动及进气道/燃气发生器/喷管调节时，补燃室压力、结尾正激波位置、发动机推力的阶跃响应特性进行分析。

(1)马赫数扰动

飞行马赫数扰动及其引起的发动机响应如图3所示。飞行马赫数增大，结尾正激波上游马赫数增大，入口冲量增大，正激波迅速向下游移动，推力减小；同时，捕获流量增加并传播到下游，使得补燃室压强逐渐增大，进而引起结尾正激波又逐渐向上游移动，稳态位置位于初始位置下游，推力逐渐增加，稳态值小于初始值。

表1 巡航状态下参数初值Table 1 Trim values at cursing condition

图2 多变量调节固冲发动机动力学模型简图Fig.2 Sketch of dynamic model of compound- adjustment ducted rocket

(2)高度扰动

高度扰动及其引起的发动机响应如图4所示。高度增加造成激波上游压力减小，入口冲量减小，因此正激波迅速向上游移动，推力增大；同时，捕获流量减小并向下游传播，引起补燃室压强逐渐下降，结尾正激波又逐渐向下游移动，稳态位置位于初始位置上游，推力逐渐减小，稳态值小于初始值。

图3 发动机对马赫数扰动的响应Fig.3 Response to mach number disturbance

图4 发动机对高度扰动的响应Fig.4 Response to height disturbance

(3)攻角扰动

攻角扰动及引起的发动机各参数响应如图5所示。攻角增加造成正激波上游压力和捕获流量增大，正激波迅速向下游移动，发动机推力突然减小；流量扰动传播到下游后，补燃室压强增大，引起正激波逐渐向上游移动，稳态位置位于初始位置上游，推力逐渐增大，稳态值大于初始值。

(4)进气道调节

进气道调节楔板折角调节及其引起的发动机各参数响应如图6所示。进气道调节造成正激波上游总压增大，正激波迅速向下游移动，并造成补燃室压力突然增大，推力增大；但由于进气道捕获流量及喷管的流通能力均未发生改变，补燃室压力和推力逐渐恢复到初始值。也就是说，进气道调节仅会改变结尾正激波位置的稳态值，而不会影响补燃室压强和推力的稳态值，且其动态过程中的扰动量也很小，可忽略。

图5 发动机对攻角扰动的响应Fig.5 Response to incidence angle disturbance

(5)燃气流量调节

燃气发生器喷管喉道面积调节及其引起的燃气发生器、发动机响应如图7和图8所示。

燃气发生器喷管喉道变小，造成燃气流量突然减小，然后又随着燃烧室压强的逐渐增大而增大，稳态值大于初始值。

由于燃气流量的响应特性，补燃室压强先减小、后增大，结尾正激波先向下游移动，然后再向上游移动，发动机推力先减小、后增大。结尾正激波稳态位置位于初始位置上游，补燃室压强及推力的稳态值大于初始值。

(6)喷管调节

冲压喷管调节及其引起的发动机各参数响应如图9所示。喷管喉道面积变大时，排出的流量突然增大，推力增大；此后，补燃室压力逐渐减小，使得结尾正激波向下游移动，喷管出口冲量逐渐减小，推力随之减小，稳态值小于初始值。

对比燃气流量调节和喷管调节的响应曲线可发现，燃气流量调节对推力有较大的影响，而喷管调节对补燃室压强有较大的影响。

图6 发动机对进气道调节的响应Fig.6 Response to inlet adjustment

图7 燃气发生器调节响应Fig.7 Response of gas-generator

2.3 传播过程分析

发动机的响应曲线中，同时给出了采用不同扰动传播过程处理方法的结果，分别是不考虑传播过程、采用延迟环节及惯性环节处理扰动传播过程。

对比是否考虑扰动传播过程的响应曲线，发动机上游发生扰动时，正激波及推力立即响应，考虑扰动向下游传播的动态过程时，补燃室压强的响应及其引起的正激波、推力等参数的进一步变化呈现出一定的滞后。而发动机下游发生扰动时，补燃室压力立即响应，并向上游传播，引起正激波的响应，由于时间常数非常小，压力扰动传播的动态过程对响应特性几乎无影响。

图8 发动机对燃气发生器调节响应Fig.8 Response to gas-generator adjustment

图9 发动机对喷管调节响应Fig.9 Response to nozzle adjustment

扰动传播过程2种处理方法的差别体现在扰动发生后参数最初的响应上。当采用延迟环节处理时，扰动发生后，经过一个延迟环节引起其他位置的相关参数响应，进而引起发动机的动态响应；当采用惯性环节处理时，扰动与其他位置相关参数响应及其引起的发动机动态响应之间存在一个惯性环节。

在线性动力学建模中，一般采用延迟环节处理扰动的传播过程[4-6]，得到的模型形式简单，有利于控制系统设计中使用；而在非线性动力学建模中，一般采用惯性环节处理扰动的传播过程[11-12,14]，得到的模型阶次相对较高，但较准确。

3 结论

(1)建立了固冲发动机各部件的性能/平衡模型、动力学模型及扰动传播模型，并将其综合为多变量调节固冲发动机非线性动力学模型。

(2)对飞行条件扰动及进气道/燃气发生器/喷管调节时，发动机各参数的变化规律进行了仿真，分析了补燃室压强、结尾正激波位置以及发动机推力的响应特性。结果表明，进气道调节不会改变推力和补燃室压强的稳态值，燃气流量调节对推力有较大影响，而喷管调节对补燃室压强有较大影响。

(3)分析了扰动传播过程对发动机动态响应的影响，对于发动机上游及下游扰动，扰动传播过程对发动机响应的影响程度不同；分析了2种扰动传播处理方法的差别及应用范围，线性动力学建模一般采用延迟环节处理，非线性动力学建模一般采用惯性环节处理。

(4)本文建立的多变量调节固冲发动机动力学模型考虑了固冲发动机中主要的动力学过程，模型简单精确，对多变量调节固冲发动机控制系统的设计具有重要意义。

[1] 徐东来,陈凤明,蔡飞超,等.固体火箭冲压发动机设计问题分析[J].固体火箭技术,2010,33(2):142-147.

[2] 蔡飞超,陈凤明,徐东来,等.宽马赫数固定几何进气道设计问题研究[J].固体火箭技术,2010,33(2):163-166.

[3] XU Dong-lai,CHEN Feng-ming,CAI Fei-chao,et al.Study on fixed-geometry supersonic inlet design for wide Mach number range application[J].Journal of Solid Rocket Technology,2010,33(1):45-48.

[4] Herbert G Hurrell.Simplified theory for dynamic relation of ramjet pressure and fuel flow[R].NACA RM E57I13.

[5] NIU Wen-yu,BAO Wen,CUI Tao,et al.Dynamic modeling and model reduction order of controllable flow solid ducted rockets[J].Journal of Solid Rocket Technology,2008,31(4):325-330.

[6] 牛文玉.燃气流量可调的固体火箭冲压发动机控制方法研究[D].哈尔滨:哈尔滨工业大学,2009.

[7] 刘华,雍雪君,梁俊龙,等．超声速进气道及冲压发动机动态特性分析[J].火箭推进,2012,38(3):17-22.

[8] 钱柏顺．冲压发动机线性动力学[J].航空动力学报,1990,5(2):179-181.

[9] Ross G Willoh.A mathematical analysis of supersonic inlet dynamics[R].NASA TN D-4969.

[10] Gary L Cole,Ross G Willoh.Analysis of the dynamic response of a supersonic inlet to flow-field perturbations upstream of the normal shock[R].NASA TN D-7839.

[11] Nitin K Gupta,Basant K Gupta,Narayan ananthkrishnan,et al.Integrated modeling and simulation of an air-breathing combustion system dynamics[C]//AIAA Modeling and Simulation Technologies Conference.Hilton Head,South Carolina,August 2007.

[12] Kumar P Bharani Chandra,Nitin K Gupta,Ananthrishnan N,et al.Modeling,simulation and controller design for an air-breathing combustion system[J].Journal of Propulsion and Power,2010,26(3):562-574.

[13] Park Ik-soo,Kim Sun-kyoung,Yeom Hyo-won,et al.Control-oriented model for intake shock position dynamics in ramjet engine[J].Journal of Propulsion and Power,2011,27(2):499-503.

[14] Park Ik-soo,Ananthrishnan N,Tahk Min-jea,et al.Low-order model for buzz oscillations in the intake of a ramjet engine[J].Journal of Propulsion and Power,2011,27(2):503-506.

[15] John J Mahoney.Inlets for supersonic missile[M].AIAA Education Series,2004.

[16] 鲍福廷,黄熙君,张振鹏．固体火箭冲压组合发动机[M].北京:中国宇航出版社,2006.

[17] 陈汝训．固体火箭发动机设计与研究(上)[M].北京:宇航出版社,1991.

[18] Jack D Mattingl．飞机发动机控制-设计系统分析和健康监视[M].北京:航空工业出版社,2012.

[19] Douglas G MacMartin.Dynamics and control of shock motion in a near-isentropic inlet[J].Journal of Aircraft,2004,41(4):846-853.

(编辑：崔贤彬)

Dynamic modeling and simulation of multivariable-adjustable ducted rocket

SHAO Ming-yu,WANG Zhi-gang

(School of Astronautics,Northwestern Polytechnical University,Xi'an 710072,China)

The equilibrium model,dynamic model of each component of multivariable-adjustable ducted rocket and the disturbance propagation model were built,and synthesized into the dynamic model of multivariable adjustable ducted rocket.Based on this model,the response of ducted rocket to the flight condition disturbance and inlet/gas-generator/nozzle adjustment was simulated and analyzed.The effects of disturbance propagation dynamic process and its treatment method on ducted rocket were also studied.The results show that,the steady-state value of thrust and combustor pressure won’t be changed due to inlet adjustment,while the gas generator adjustment and nozzle adjustment have great influence on thrust and combustor pressure respectively.

ducted rocket;multivariable-adjustment;dynamic modeling

2015-04-08；

：2015-06-05。

邵明玉(1988—)，男，博士生，研究方向为冲压发动机设计。E-mail：mingyupiaoxue@126.com

V438

A

1006-2793(2015)06-0782-07

10.7673/j.issn.1006-2793.2015.06.006