二次燃烧对燃气弹射载荷和内弹道影响数值研究

胡晓磊，王 辉，乐贵高，马大为，于存贵

(1.南京理工大学 机械工程学院，南京 210094; 2.中国航天科技集团公司第七研究院 第七设计部，成都 610100)



二次燃烧对燃气弹射载荷和内弹道影响数值研究

胡晓磊1，王 辉2，乐贵高1，马大为1，于存贵1

(1.南京理工大学 机械工程学院，南京 210094; 2.中国航天科技集团公司第七研究院 第七设计部，成都 610100)

为了研究二次燃烧对燃气弹射载荷和内弹道的影响，采用有限速率/涡耗散模型模拟初容室内燃气射流与空气的二次燃烧过程，运用域动分层网格更新方法，对导弹尾罩运动区域进行更新。在与实验对比验证的基础上，数值研究了二次燃烧对初容室流场、载荷和内弹道的影响。结果表明，文中建立的数值方法是可靠的，能够有效地捕捉二次燃烧过程中出现的初始压强峰值；富燃燃气与空气发生的二次燃烧使流场温度、压力和载荷高于无二次燃烧流场，而且使导弹出筒时间提前。研究结果可为燃气射流内弹道和结构设计提供理论基础。

燃气弹射；二次燃烧；动网格；载荷；内弹道

0 引言

燃气弹射是指导弹依靠燃气发生器产生的推力推动导弹弹射出发射筒的发射方式。燃气弹射作为一种高技术作战武器，具有体积小、能量大、发射装置简单和机动性强等优点[1-2]，得到越来越多国家的青睐。随着低温推进剂技术的发展，低温推进剂已经成功地应用到燃气发生器中。由于低温推进剂燃烧之后产生大量的富燃气体，主要有CO和H2。富燃气体进入发射筒后，与初容室内氧气发生混合，容易产生非预混二次燃烧现象[3]，并对弹射内弹道和初容室结构产生热冲击。

针对非预混燃烧现象，国内外主要采用有限速率/涡耗散方法进行研究。Guessab等[4]采用有限速率/涡耗散模型，研究了非预混甲烷燃烧过程。结果表明，该数值方法预测的甲烷燃烧温度和压力与实验结果吻合较好。Luan等[5]采用有限速率/涡耗散方法和气固两相流理论，研究了煤的燃烧。结果表明，该方法能有效地分析煤的燃烧过程。迟宏伟等[6]运用热解气体有限速率/涡耗散模型，研究了冲压发动机燃烧室中PMMA自点火性能。冯喜平等[7]采用有限速率/涡耗散模型，研究了含硼富燃燃气二次燃烧过程。结果表明，该模型能很好地预测二次燃烧流场压力参数。

本文以燃气弹射装置为物理模型，采用有限速率/涡耗散模型，建立包含导弹运动的初容室内燃气与空气二次燃烧模型，研究二次燃烧对初容室流场、弹射内弹道和载荷特性的影响规律，为燃气弹射内弹道和弹射动力装置结构设计提供理论基础。

1 物理模型和计算方法

1.1 物理模型

燃气弹射系统包括燃气发生器、导流锥、发射筒、底座和尾罩等，如图1所示。其中，P1、P2和P3分别为观测点，P1点位于导流锥腰部，P2点位于底座处，P3点置于发射筒壁面处。其工作原理是推进剂在燃气发生器中燃烧后，经喷管进入初容室，与初容室中空气混合和掺混，产生二次燃烧现象，推动尾罩和尾罩上导弹弹射出发射筒。

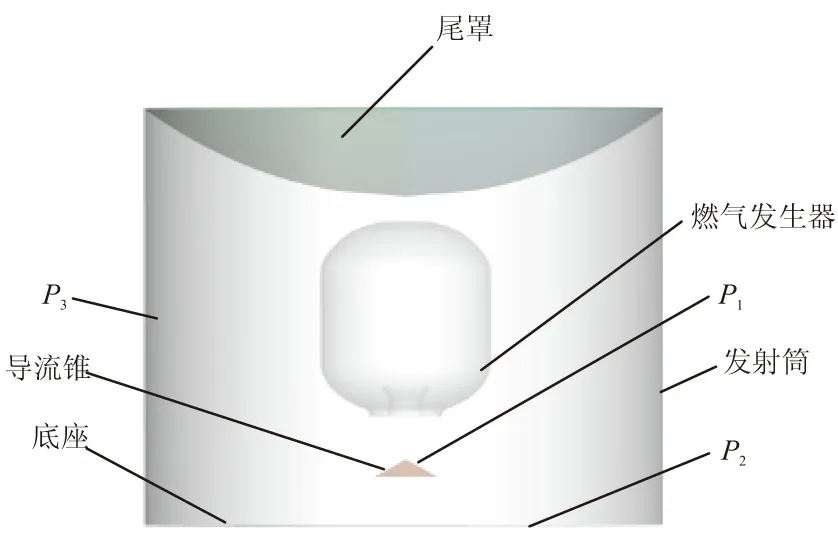
图1 燃气弹射装置结构示意图Fig.1 Sketch of gas-ejection launcher

1.2 数值计算方法

1.2.1 控制方程

针对燃气弹射装置轴对称结构特点，采用二维轴对称多组分Navier-Stokes控制方程：

(1)

其中

式中 各变量符号见文献[8]。

1.2.2 湍流模型

新鲜的富燃燃气进入发射筒，与筒内空气发生激烈化学反应。本文选用RNGk-ε湍流模型。该模型适合完全湍流流动，是一种针对高Re数的湍流计算模型。

湍流动能方程(k方程)为

Gk+Gb-ρmε

(2)

湍流能量耗散率方程(ε方程)为

(3)

式中k和ε分别为湍流动能和耗散率；μ为混合物粘性；ρk=1.0；Gk为由于平均速度梯度引起的湍流动能k的产生项；Gb为由浮力引起的湍流动能k的产生项；σε=1.3；Cε1=1.44；Cε2=1.92。

1.2.3 有限速率/涡耗散模型

有限速率模型忽略湍流脉动对化学反应过程的影响，反应速率根据Arrhenius公式确定。

考虑以下形式的第r个反应：

(4)

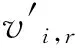
反应r中物质i产生/分解摩尔速率由式(5)给出：

(5)

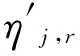
涡耗散模型又称为湍流-化学反应相互作用模型，反应速率由湍流混合时间尺度k/ε控制。

(6)

(7)

(8)

式中YR为反应物质量分数；YP为燃烧产物质量分数；A为常数，A=4.0；B为常数，B=0.5。

在非预混火焰反应区发生快速燃烧时，只要湍流出现，反应即可开始且不受限制，反应速度往往较快。因此，有限速率/涡耗散模型被广泛用于湍流扩散燃烧的数值模拟中。有限速率/涡耗散模型的净反应速率Ri由Arrhenius化学动力学和涡耗散反应速率混合控制，Arrhenius反应速率作为动力学开关，阻止反应的火焰稳定之前发生，延迟了计算中化学反应的开始，较为符合实际[9]。

文中气相组分燃烧模型采用文献[9]中CO/H2燃烧模型：

2CO + O2→ 2CO2+Q1(Q1= 565.95 kJ/mol)

2H2+ O2→ 2H2O +Q2(Q2= 563.64 kJ/mol)

1.2.4 导弹运动规律

弹射过程中，导弹沿着发射筒轴线向上运动。轴线方向上，导弹受到燃气推力、重力和摩擦力等3个力。导弹加速度根据牛顿第二定律，由导弹受力进行计算，其合外力为

F=Fgas-Mg-Fm

(9)

式中Fgas为燃气推力；M为导弹质量；g为重力加速度；Fm为摩擦力。

t时刻的导弹沿轴线方向的速度v1和位移lt分别由下式求得。其中，Δt为时间步长。

vt=vt-Δt+(F/M)Δt

(10)

lt=lt-Δt+vt×Δt

(11)

式(10)和式(11)分别给出导弹在任一时刻的运动速度和位移，采用域动分层网格更新方法[10]，对网格进行更新。在导弹弹射过程中，导弹尾罩为运动边界，其他为静止边界。导弹底部网格节点之间满足胡克定律，当网格节点应力增加或减小时，网格节点位移也随之增加或减小。在网格节点位移增加或减小超过指定高度时，网格之间产生分裂或缩并，从而实现弹射过程中导弹底部网格的动态更新。

1.2.5 网格模型和边界条件

燃气弹射初容室内流场数值计算网格模型如图2所示。计算从燃气发生器喷管入口处开始计算，燃烧室总压随时间变化规律如图3所示，初始温度为0.57T0(无量纲化值)。发射筒壁面、燃气发生器壁面和喷管壁面等固壁处，采用绝热壁面边界条件。使用NASA的CEA软件，对推进剂燃烧产物进行热力学计算，得到喷管入口处气体组分的质量分数，如表1所示。计算开始时，初容室内为标准大气状态。其中，N2的质量分数为0.77，O2的质量分数为0.23。

图2 网格模型Fig.2 Mesh model

图3 燃烧室压力曲线Fig.3 Pressure curve of combustion chamber

表1 燃烧室组分质量分数Table 1 Species and mass fraction of inlet

采用有限体积法离散控制方程，压力梯度项采用Standard格式离散，动量方程的差分格式选用二阶迎风格式，湍流输运方程的差分格式采用一阶迎风格式，压力-速度耦合采用SIMPLE算法。

2 数值方法验证

2.1 网格无关性验证

由于燃气射流二次燃烧流场的数值计算精度对网格数目有较强的依赖性，因此需要进行网格无关性检验。建立3种网格工况下流动模型，其中工况A为6.5万计算网格，工况B为5.5万计算网格，工况C为1.2万计算网格。选取P1点为观测点，分别将工况A和工况C在5 ms和10 ms时刻的温度和压力值与工况B进行对比，如表2所示。从对比结果来看，工况A与工况B之间P1点温度和压力最大误差百分比为0.01，而工况C与工况B之间观测点温度和压力最大误差百分比为-0.11，这可能是由于工况C网格稀疏和数值耗散导致的。由此可见，工况A和工况B的计算结果较为一致。综合考虑计算过程中弹底网格数量的增加以及数值计算效率和计算精度等方面因素，选用工况B的网格进行燃气弹射流场二次燃烧分析。

表2 网格无关性实验结果Table 2 Results of grid independence

2.2 数值方法验证

为了验证数值方法的有效性，分别采用文献[3]中的11组分12步基元反应机理和文献[3]中的燃烧机理进行仿真分析，并与实验结果进行对比，结果如图4所示。从P3点压力曲线对比可看出，采用文献[3]中的基元反应模型计算结果偏低，而两步总反应燃烧模型与实验值吻合较好。这可能是由于文中采用的低温推进剂湍流燃烧机理与文献[3]中的高温推进剂燃烧机理不同导致的。因此，文中采用两步总反应燃烧机理，对初容室内二次燃烧流场进行研究和分析。

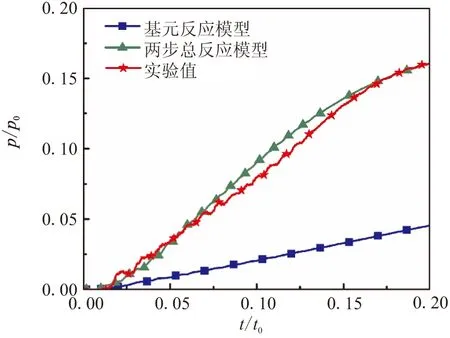
图4 P3点数值与实验结果对比Fig.4 Comparison of numerical and experimental results at point P3

3 结果与分析

3.1 流场分析

为研究二次燃烧对初容室内温度、压力、马赫数和组分分布的影响，选取0.2t0时刻的流场进行分析。图5为0.2t0时刻初容室内有/无二次燃烧无量纲温度场和压力场云图对比。其中，上半部分是无二次燃烧流场温度和压力云图，下半部分是含二次燃烧温度和压力云图；图6为0.2t0时刻流场典型组分的质量分数分布云图，图7为0.2t0时刻有/无二次燃烧马赫数和流线图对比。其中，上半部分为流线图；下半部分是马赫数图。

从初容室内温度场和压力场云图可见，含有二次燃烧的流场温度和压力均高于无二次燃烧流场值。这主要是由于含二次燃烧的初容室流场发生剧烈的放热化学反应，导致流场温度升高。而在0.2t0时，导弹的位移很小。根据理想气体状态方程，温度升高时，伴随压力升高，因而含二次燃烧流场的温度和压力均高于无二次燃烧值。在无二次燃烧流场中，燃烧室产生的燃气经喷管加速排出，并形成膨胀波。由于无化学反应释放能量，燃气射流的温度和压强自然衰减。从温度场云图还可看出，含二次燃烧的燃气射流边界层处温度明显高于无二次燃烧的温度；而在燃气射流核心区域，有无化学反应两者的温度相差并不大。这是由于从燃气发生器排出的燃气射流不断卷吸初容室内空气，边界层处的高温富燃气体与附近氧气发生化学反应，耗尽了边界层处的氧气。在燃气射流核心区域，由于氧气浓度太低，富燃燃气无法发生化学反应，因此燃气射流核心区域温度相差不大。从初容室流场温度分布来看，喷管喷出的燃气射流经过导流锥分流后，一部分气体在导流锥下方聚集，另一部分沿着底座和发射发射筒壁面向尾罩方向流动。

(a) 温度场 (b) 压力场

图5 0.2t0时刻温度和压力无量纲云图对比

Fig.5 Dimensionless comparison of temperature and pressure contours at 0.2t0

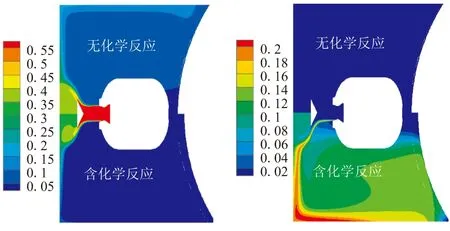
从图6中0.2t0时刻有/无二次燃烧的CO、CO2、O2和N24种组分的分布云图看出，无二次燃烧的流场CO质量分数高于含二次燃烧流场，而CO2的质量分数低于含二次燃烧。这是由于含二次燃烧的流场中发生了2CO+O2→ 2CO2的化学反应，使CO转化为CO2，同时消耗初容室中的O2。因此，含二次燃烧流场中，CO质量分数降低，CO2质量分数升高，O2含量降低。由于流场中N2没有参加化学反应，因此可用N2的质量分数表示燃气与空气的质量交换情况。从图6中可见，初容室中燃气与空气发生质量交换的区域主要分布在燃气射流两侧，在燃气射流核心区域几乎没有N2。

(a) CO (b) CO2

(c) O2(d) N2

图6 0.2t0时刻流场组分云图分布对比

Fig.6 Comparison of mass fraction contour at 0.2t0

从图7(a)和(b)中马赫数与速度流线图可看出，无论是否含有二次燃烧，二维轴对称流场中都存在2个漩涡。其一，由于导流锥的分流作用，在导流锥底部形成的漩涡；其二，燃气沿着发射筒壁面流动形成漩涡。这些漩涡使无二次燃烧流场中燃气加速扩散，使得二次燃烧流场燃气与空气加速反应，释放化学能。

(a) 无化学反应 (b) 含化学反应

图7 2t0时刻马赫数和流线图对比

Fig.7 Comparison of mach contours and streamlines at 0.2t0

3.2 载荷特性

为深入研究二次燃烧对载荷的影响规律，分别选取3个观测点进行载荷分析，如图1。图8和图9分别为初容室内观测点温度和压力载荷随时间变化曲线。图10为初容室内氧气质量分数随时间变化曲线。

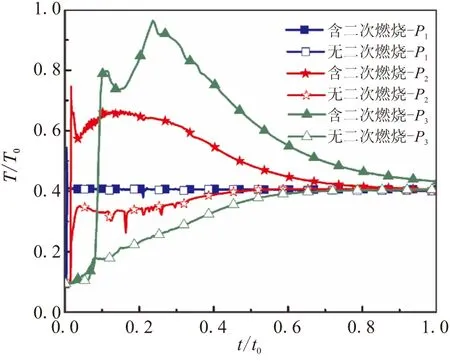
图8 观测点温度随时间变化曲线Fig.8 Temperature curve of monitor point

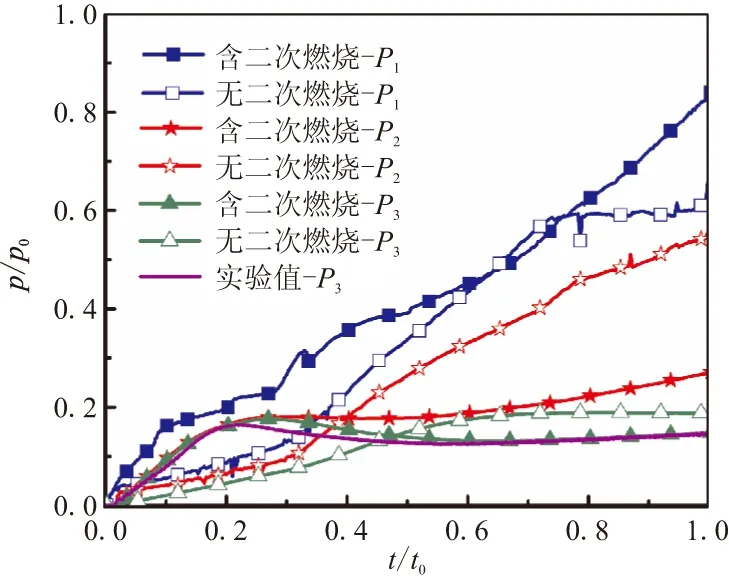
图9 观测点压力随时间变化曲线Fig.9 Pressure curve of monitor point

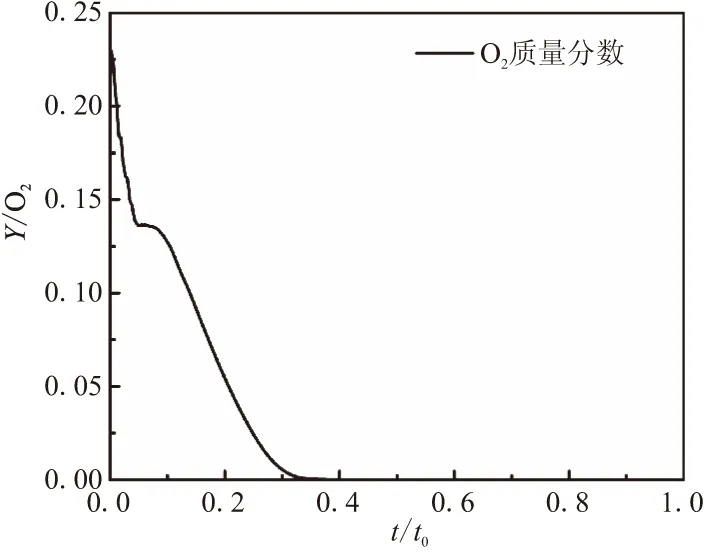
图10 氧气质量分数随时间变化曲线Fig.10 Mass fraction curve of O2

从图8中3个观测点温度随时间变化曲线可看出，含二次燃烧流场观测点温度具有如下趋势：在0～0.6t0时间内，离喷管越远的观测点温度越高，各观测点温度先升高、后降低；在0.6t0时刻之后，各观测点温度趋近于燃气发生器总温。其中，在0.002t0时刻，P1点温度峰值为0.53T0；在0.16t0时刻，P2点温度峰值为0.74T0；在0.24t0时刻，P3点温度峰值为0.96T0。这是由于含二次燃烧的流场中，燃气射流离喷管越远，其与空气的接触面越大，发生化学反应越剧烈，释放的化学能越高，温度也越高。无二次燃烧流场观测点温度趋势与含二次燃烧流场观测点温度相反：在0～0.6t0时间内，离喷管越远的观测点温度越低，各观测点温度逐渐升高；在0.6t0时刻之后，各观测点温度趋近于燃气发生器总温。图9为观测点压力随时间变化曲线以及P3点压力试验曲线。从P3点仿真曲线和实验曲线可见，2条曲线趋势一致，吻合较好。在0～0.23t0时间内，P3点压力由0增加到0.18p0；在0.23t0～0.6t0时间内，P3点压力由0.18下降到0.12p0；在0.6t0～1.0t0又由0.12p0上升到0.14p0。而无二次燃烧流的P3点压力一直在增加，与实验曲线误差较大。由此可进一步证明文中数值方法的有效性。结合图10中氧气的质量分数变化规律可看出，在0.23t0出现初始压强峰值的原因，是由于初容室内富燃燃气与氧气发生放热的二次燃烧，造成压力突然上升。

3.3 弹道特性分析

图11为含二次燃烧和无二次燃烧燃气弹射弹道参数随时间变化曲线。为了量化分析，假设发射筒长度为0.35l0。通过比较有/无二次燃烧出筒时间可见，含二次燃烧出筒时间为0.69t0，无二次燃烧出筒时间为1.0t0。二次燃烧使得导弹出筒时间缩短31%。通过对比有/无二次燃烧加速度曲线，发现虽然在出筒时刻，含二次燃烧的导弹出筒加速度(0.44a0)比无二次燃烧的出筒加速度(0.62a0)低29%，但在0.23t0时刻含二次燃烧导弹出现值为0.65a0加速度峰值。根据牛顿运动定律，结合上节中发射筒壁P3点的压力随时间变化曲线可知，这是由于二次燃烧产生的初始压强峰值导致的。从有/无二次燃烧导弹速度曲线可看出，含二次燃烧导弹出筒速度为0.58v0，无二次燃烧速度为0.55v0。可见，二次燃烧使得导弹出筒速度升高了5%。

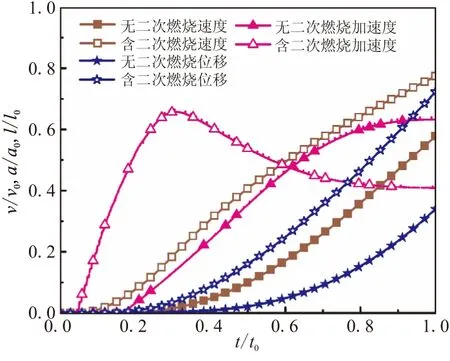
图11 弹道变化曲线Fig.11 Curve of missile trajectory

4 结论

(1)建立了耦合二次燃烧和内弹道的燃气弹射数值模型，采用有限速率/涡耗散模型模拟初容室内燃气射流与空气的二次燃烧过程。通过与实验结果对比，验证了数值方法的有效性，捕捉到了初始压强峰值。

(2)密闭的初容室内，由于燃气与空气中O2发生激烈的放热氧化反应，导致二次燃烧流场温度、压力和载荷均高于无二次燃烧流场。

(3)基于发射筒长度为0.35l0的分析可见，二次燃烧使导弹出筒时间缩短31%，出筒加速度下降29%，出筒速度升高5%。但含二次燃烧的导弹在0.25t0时刻存在一个初始加速度峰值。

(4)通过以上分析，在燃气弹射流场、载荷和内弹道分析时，需要考虑二次燃烧的影响。

[1] 蒋瑞岗.导弹的弹射与燃气发生器设计[J].现代防御技术,1998,26(3):9-16.

[2] 袁曾凤.火箭导弹弹射内弹道学[M].北京：北京工业学院出版社,1987.

[3] 张光喜,周为民,张钢锤,等.固体火箭发动机尾焰流场特性研究[J].固体火箭技术,2008,31(1):19-23.

[4] Guessab A,Aris A,Bounif A.Simulation of turbulent piloted methane non-premixed flame based on combination of finite-rate/eddy-dissipation model[J].Mechanika,2013,19(6):657-664.

[5] Luan Yan Tsan,Chyou Yau-Pin,Wang Ting. Numerical analysis of gasification perform via finite-rate model in a cross-type two-stage gasifier[J].International Journal of Heat and Transfer,2013,57(2):558-566.

[6] 迟宏伟,魏志军,王利和,等.固体燃料超燃冲压发动机燃烧室中PMMA自点火性能数值研究[J].推进技术,2014,35(6):799-808.

[7] 冯喜平,刘洋,任全彬,等.基于King 模型的含硼富燃燃气燃烧模拟[J].固体火箭技术,2014,37(2):209-213.

[8] 胡晓磊,乐贵高,马大为,等.同心筒发射燃气射流二次燃烧数值研究及导流板改进[J].兵工学报,2014,35(1):62-69.

[9] 冯喜平,李海波,唐金兰,等.采用不同气相燃烧模型模拟含硼燃气扩散燃烧过程[J].固体火箭技术,2013,36(4):474-480.

[10] 姜毅,郝继光,傅德彬.导弹发射过程三维非定常数值模拟[J].兵工学报,2008,29(8)：911-915.

(编辑：崔贤彬)

Influence of secondary combustion on the load and internal trajectory of gas-ejection launcher

HU Xiao-lei1, WANG Hui2, LE Gui-gao1, MA Da-wei1, YU Cun-gui1

(1.School of Mechanical Engineering, NUST, Nanjing 210094, China; 2.The Seventh Design Department, Aerospace Science and Technology Corporation, the Seventh Research Institute, Chengdu 610100, China)

To study the influences of secondary combustion on the load and internal trajectory of gas-ejection launcher, the Finite-Rate/Dissipation model was adopted to simulate the secondary combustion process of air and jet flow and the dynamic mesh update method was used to update the moving zone below tail cover. Compared with experimental results, the influence of secondary combustion on the flow field in initial chamber, load, and internal trajectory were studied.The results show that the numerical method is reliable and it can capture the initial pressure peak during secondary combustion. And secondary combustion can enhance temperature,pressure,load,and the time of missile out of tube is shortened.The research can provide theoretical basis for the internal trajectory and structure design.

gas-ejection;secondary combustion; moving mesh;load;internal trajectory

2014-07-23；

：2014-10-30。

胡晓磊(1987—)，男，博士生，研究方向为兵器发射理论与技术。E-mail:hu0423@126.com

V438

A

1006-2793(2015)06-0776-06

10.7673/j.issn.1006-2793.2015.06.005