一种新的基于ARIMA 模型的粮食产量预测

杨铁军，杨 娜，朱春华，张 元

（河南工业大学 信息科学与工程学院，河南 郑州 450001）

0 引言

新中国成立以来，我国粮食产量得到大幅度提高，同时粮食生产也呈现出周期性震荡上升态势[1].为了能够有效地调节我国粮食供给与需求之间的关系，对未来粮食产量的预测研究就显得十分必要.目前国内外学者提出了多种基于统计学原理的粮食产量预测模型，大体上可以分为三类：第一类是经济发展模型，它侧重于社会经济发展因素对粮食产量的长期影响；第二类是气候模型，它侧重于气象因素引起的粮食产量的波动；第三类是时间序列模型，它侧重于对变量之间进行因果分析，探究各因素之间的联系[2-5].作者在建立第三类模型的基础上，尝试以1949—2011 年粮食实际产量为基础数据，分别使用传统[6-8]和改进算法构建差分自回归移动平均（Autoregressive Integrated Moving Average Model,ARIMA）模型，阐明上述两种算法的差异性，对我国粮食的趋势产量进行预测，并分析其预测性能的优缺点，为宏观调控部门更为有效地进行调控给予技术支持.

1 ARIMA 模型预测

1.1 预测原理

ARIMA 模型预测的基本思想是：将预测对象随时间推移而形成的数据视为一个随机时间序列，根据时间序列模型的识别规则，建立相应的模型.ARIMA 模型根据原序列是否平稳以及回归中所含部分的不同，包括移动平均过程（MA）、自回归过程（AR）、自回归移动平均过程（ARMA）以及ARIMA过程.简言之，ARIMA 模型是指将非平稳时间序列转化为平稳时间序列，然后仅对因变量的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型[9].

令ωt=（1-L）dyt，其中，yt是d 阶单整序列，ωt为平稳序列[10]，在t 时刻的观测值，则ARMA 的一般模型可以表示为：

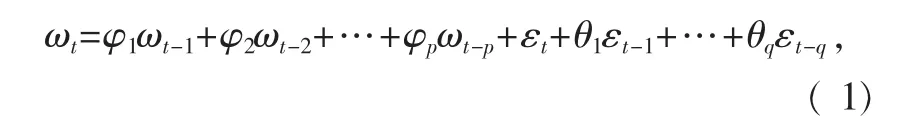
式中：p，q 分别被称为自回归阶数和平均阶数.

设L 为滞后算子[7]，则

式（1）用滞后算子表示为：

式中：φ（L）=1-φ1L-φ2L2-…-φpLp；Θ（L）=1+θ1L+θ2L2+…+θqLq.

经过d 阶差分 变换后，（3）式表示ARMA（p，q）模型变为ARIMA（p，d，q）模型.

式中：εt是均值为0、方差为σ2的白噪声过程[10].

1.2 ARIMA 模型粮食产量预测仿真流程（图1）

图1 ARIMA 模型粮食产量预测仿真流程Fig.1 The simulation process of grain output prediction based on ARIMA model

运用传统算法和改进算法建立粮食产量预测ARIMA 模型的仿真流程分别如图1（a）和图1（b）所示.这两种预测模型的不同之处在于，第一，前者是通过观察波形变化趋势来判断差分阶次，后者则采用ADF 单位根检验的方法确定[11-12]；第二，前者用AIC 准则直接确定出模型参数，后者对所确立的模型参数进行模型适应性检验得到最优模型.

1.2.1 平稳性检验

ADF 单位根检验根据观测值的DF 统计量判断序列平稳性.首先建立零假设（H0）和备择假设(H1)，其中H0为β＝1；H1为β＜1.在零假设成立条件下，定义DF 统计量，

计算原始序列的DF 值是否在1%、5%和10%的临界值下都接受假设条件.若DF＞临界值，则接受H0，yt非平稳；DF＜临界值，则拒绝H0，yt平稳.

1.2.2 模型识别与定阶

自相关分析法是进行时间序列分析的有效方法，它简单易行，较为直观.根据绘制的自相关分析图和偏自相关分析图，可以初步识别平稳序列的模型类型和模型阶数.ARMA 模型的3 种基本形式AR（p）、MA（q）、ARMA（p，q）的相关性特征如表1 所示.

表1 相关性特征Table 1 Correlation characteristics

根据表1 所示的模型相关性特征，可利用自相关函数与偏相关函数的截尾性来识别模型类型，并利用偏相关函数（PACF）确定AR 模型的滞后阶数；利用自相关函数（ACF）确定MA 模型的滞后阶数.

1.2.3 模型参数估计

时间序列分析模型的模型结构和阶数经过初步识别后，要对模型参数进行估计.模型参数的估计方法大体上分为3 类：最小二乘估计、矩估计和利用自相关函数的直接估计.采用最小二乘方法来估计模型参数.

已知样本观测值（yi，xi）（i=1，2，…，n），假如参数估计量为，则

1.2.4 残差检验

对1.2.3 中所估计的模型参数的适应性进行检验，实质是对模型残差序列进行白噪声检验.若残差序列不是白噪声，说明还有一些重要信息没被提取，应对拟合模型进行重新设定，直至得到最优模型.

计算观测值与拟合值的残差，根据其Durbin-Watson（DW）值判别其是否存在自相关.假设残差ut存在一阶自相关，

那么基于经典线性模型，假定采用普通最小二乘法回归得到的残差存在,

DW 值一般在2 左右则不存在自相关，但需要对残差做进一步分析，对生成的残差序列进行相关性检验，若出现截尾特性，则残差不存在自相关，说明模型拟合较好.

1.2.5 模型预测

预测方法一般分为动态预测和静态预测.评价预测方法的指标有平均绝对百分误差、Theil 不等系数和预测均方差，其中Theil 不等系数和预测均方差应用较为广泛.Theil 不等系数越靠近0，表示单位误差均方根越小，即预测值与实际值越靠近，模型拟合精度越高.预测均方差包括3 个指标：偏差比、方差比和协方差比，三者之和为1，预测精度越高，偏差比率和方差比率越小，协方差比率越大.根据给定的观测数据的特点，选用静态预测方法进行模型预测.

1.3 仿真结果

我国粮食产量相关数据来自于《中国统计年鉴》[8]（1949—2011 年），我国的主要粮食是谷物、豆类和薯类，其中谷物包含稻谷、小麦和玉米.运用两种算法对不同的年份区间进行仿真得到的ARIMA 模型参数如表2 所示，其中M1=20（1949—1968 年），M2=40（1949—1988 年），M3=60（1949—2008 年）.运用这两种算法得到的预测数据与原始数据分别如图2 所示.

表2 不同年份区间的ARIMA 模型参数Table 2 ARIMA model parameters of different years interval

图2 3 个年份区间的ARIMA 预测数据Fig.2 ARIMA forecast data of the three year interval

图2 中M1、M2、M3 分别表 示1949—1968 年、1969—1988 年、1989—2008 年3 个样本区间的原始数据，M1F、M2F、M3F 表示用改进算法得到的3个区间的预测值，M20、M40、M60 表示用传统算法得出的3 个区间预测值.

对预测数据与原始数据进行拟合优度检验，检验结果如表3 所示.R2Adj即调整后的R2，表示在回归方程中，自变量对因变量的解释比例，这一比例越大，回归方程可以解释的部分越多，模型越精确，回归的效果越显著.R2是一个介于0 和1 的数，越接近1 说明拟合效果越好.

由表3 可以看出，在相同样本区间下，运用改进算法得到的R2更大，更能够准确地拟合原始数据；在不同样本区间下，比较同一种软件的预测结果，选取的样本数据越多，预测结果与原始数据的拟合度越高，两种软件得到的R2数据都验证了上述结论.

表3 预测数据与原始数据的拟合优度检验Table 3 Goodness of fit test with Forecast data and original data

2 结论

比较分析了粮食产量预测中使用的ARIMA 模型的仿真流程及预测拟合度性能，采用新中国建国以后的粮食产量数据，分别利用两种实现方法得出不同的样本区间的ARIMA 预测模型，其拟合优度检验结果均表明改进算法建立的ARIMA 模型预测更为精确，进一步分析传统和改进算法建立的ARIMA 建模思想并深入挖掘更高精度的模型预测方法是下一步要研究的课题.

［1］孙东升，梁仕莹.我国粮食产量预测的时间序列模型与应用研究［J］.农业技术经济，2010.

［2］高卫，张电学，雷利君，等.中国粮食产量影响因素分析及研究方法综述［J］.安徽农业科学，2014，42（33）:11954-11955.

［3］Brown L R.Who will feed China Wake up call for a small plane［M］.New York:W W Norton and Co，1995：1-10.

［4］高卫，张电学，雷利君，等.中国粮食产量影响因素分析及研究方法综述［J］.安徽农业科学，2014，42（33）：11954-11955，11958.

［5］王丹.气候变化对中国粮食安全的影响与对策研究［D］.武汉：华中农业大学，2004.

［6］Suresh K K，Krishna Priya S R.Forecasting sugarcane yield of tamilnadu using ARIMA Models［J］.Sugar Tech March，2011，13（1）:23-26.

［7］杨德平，刘喜华，孙海涛，等.经济预测方法及MATLAB 实现［M］.北京：机械工业出版社，2012.

［8］魏艳华，王丙参，王转民.基于ARIMA 模型的天水市粮食产量预测与决策［J］.天水师范学院学报，2014，3（2）:17-21.

［9］陈艳红，胡胜德，申倩.基于ARIMA 模型的中国粮食供需平衡及预测［J］.广东农业科学，2013（5）:230-234.

［10］张恒，高峰，金鑫，等.基于ARIMA 模型的我国粮食产量时间序列分析［J］.科技信息，2010，10:121-122.

［11］陈昭.时序非平稳性ADF 检验法的理论与应用［J］.广州大学学报，2008，7（5）：5-10.

［12］夏南新.单位根的DF、ADF 检验与PP 检验比较研究［J］.数量经济技术经济研究，2005（9）:129-135.

［13］国家统计局.中国统计年鉴2013［M］.北京:中国统计出版社，2014.