Research on inter-satellite measurement technique in high dynamic environment

WANG Yong-qing(王永庆), SUN Li-da(孙立达), YANG Li-yun(杨丽云),JIANG Hong-wei(姜洪伟), WU Si-liang(吴嗣亮)

(School of Information and Electronics, Beijing Institute of Technology, Beijing 100081, China)



Research on inter-satellite measurement technique in high dynamic environment

WANG Yong-qing(王永庆), SUN Li-da(孙立达), YANG Li-yun(杨丽云),JIANG Hong-wei(姜洪伟), WU Si-liang(吴嗣亮)

(School of Information and Electronics, Beijing Institute of Technology, Beijing 100081, China)

An improved measurement algorithm, based upon the theory of two-way time transfer (TWTT), is proposed to measure satellites with high speeds. The algorithm makes theoretical analyses and corresponding deductions on a relative motion model of two satellites, and eliminates the measurement error caused by the equipment delay when a satellite moves at a high speed. Theoretical analysis and simulation results demonstrate that in comparison with the conventional TWTT algorithm, the proposed algorithm can significantly enhance the measurement accuracy of the inter-satellite ranging and time synchronization, and the algorithm is more effective with the relative velocity between the satellites and transmitting delay becoming larger.

two-way time transfer; ranging; time synchronization; measurement accuracy

Satellite networking is motivated by the demand for autonomous navigation with space technique growing, whose purpose is to guarantee the network work stably and elevate the network. To accomplish autonomous navigation task, the inter-satellite ranging and time difference measurement must be high-precise[1]. The commonly used ranging algorithms include the pseudo-code method and carrier method, and the time difference algorithms include the clear method and GPS common-view method. The method of two-way time transfer (TWTT)[2-4]is widely applied in inter-satellite ranging and time synchronization. This method can not only measure distance and time difference, but also eliminate channel common error in bidirectional measurement process[5-6]. The traditional time synchronization is among one satellite responder and some ground stations[7]. In Ref. [8], TWTT algorithm was applied in distance and time difference measurement in a static model with no relative motion between the two satellites. In Refs.[9-10], the realization scheme of the algorithm which considered the relative motion between the satellites was brought up, but the measurement error brought by the satellite motion during the transmitting and receiving delay were ignored.

According to current opened references, there are few measurement algorithms taking the effect of equipment delay on the measurement algorithm into account. In Ref.[9], the algorithm just considered the equipment delay as a fixed delay of satellite’s interval from transmitting moment to receiving moment, and asserted that satellites keep relatively static when signals spread through the equipment transmitting channel and receiving channel. And the assertion confused the signals produce moment with transmitting moment and ignored satellites position changes during the equipment delay. The measurement accuracy may be affected by the error caused by satellites motion during the equipment delay, especially when satellites move at high-speed. The measurement result in Ref. [9] ignored a dynamic-changing error term which depends on the transmitting delay and the relative velocity between satellites. The relative velocity is especially larger when satellites move in different orbits, so the algorithm of ranging and time difference measurement must consider the equipment delay in high dynamic environment.

To solve the problem described above, an improved algorithm of inter-satellite ranging and time difference measurement is put forward in this paper. The algorithm takes the equipment transmitting and receiving delay into account based upon the TWTT theorem, and eliminates the measurement error caused by the satellites motion.

1 Two-way time transfer algorithm

1.1 Principle

The basic principle of the TWTT method which can be used for ranging and time difference measurement between two relative stillness satellites is given in Fig.1.

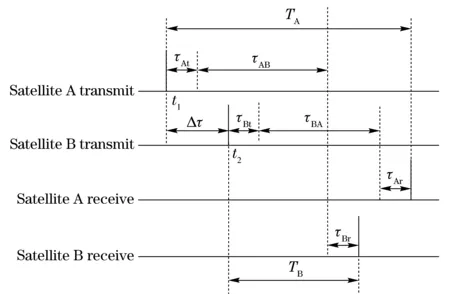
Fig.1 Principle of two-way time transfer method in inter-satellite

As shown in Fig.1, suppose that satellite A and B transmit the ranging signals without range ambiguity at their local starting second. For the sake of time differenceΔt,thetwosatellitesactuallytransmitthesignalsatthetimet1andt2separately.SatelliteA’sintervalfromtransmittingmomenttoreceivingmoment(shortfort-rinterval),whichiscalledTA,canbeobtainedbyacquiringthesignalstransmittedbysatelliteB. TAdependsonthesignalstransmissionintervalτBAfromsatelliteBtoA,satelliteB’stransmittingdelayτBt,satelliteA’sreceivingdelayτAr,andthetimedifferenceΔtbetweenthesatellites.So:

TA=Δt+τBt+τBA(t2)+τAr

(1)

Similarly,TBis satellite B’s t-r interval, which depends on the signals transmission intervalτABfrom satellite A to satellite B, satellite A’s transmitting delayτAt, satellite B’s receiving delayτBr, and the time differenceΔtbetweenthetwosatellites.Therelationisexpressedas

TB=-Δt+τAt+τAB(t1)+τBr

(2)

There isτBA=τABwhen satellite A and B transmit their ranging signals with a nearly frequency on the same transmission path at the same time. According to Eqs.(1)(2), the signals transmission interval and the distance can be expressed as

(3)

Thetimedifferencecanalsobeobtainedas

(4)

Consequently, based on TWTT, the distance and time difference between two satellites are successfully obtained at the same time.

1.2 General measurement algorithm

The condition ofτBA=τABis assumed in section 1.1, butτBAis actually not equivalent to τABwhenthetwosatelliteshaverelativemotions.Therefore,Eqs.(1)(2)shouldbereestablishedinvolvingtherelativemotions.ThenewequationsbroughtupbyRef.[9]canbeexpressedas

(5)

(6)

The general measurement algorithm applied to dynamic environment considered the relative motion and equipment delay, but just regarded the equipment delay as a fixed delay of satellite’s t-r interval. This algorithm ignored satellites motion during the equipment delay and confused the signal produce moment with transmitting moment, which would introduce error terms positively associated with the relative velocity and transmitting delay. The satellite motion is relative to real-time velocity, so the error terms must be corrected in real time.

The relative velocity between satellites in different orbits is large, so inter-satellite ranging and time synchronization algorithm must consider the satellite motion during the equipment delay, and how to eliminate the influence of transmitting and receiving delay is the key point to evaluate an algorithm designed for high dynamic environment.

2 High dynamic inter-satellite ranging and time synchronization algorithm

2.1 Improved measurement algorithm

The improved algorithm can eliminate measurement error caused by the transmitting and receiving delay of inter-satellite measurement equipment in high dynamic environment, which is compared with traditional algorithms demonstrated in Ref. [9]. The relative satellite velocity varies slowly in measuring process, so it can be considered that two satellites move with the constant satellite velocityvA,vBseparately. The relative motion model of two satellites in communication process is given in Fig.2, wherecis the propagation speed of radio wave in a vacuum.

Fig.2 Relative motion model of two satellites

The distance between satellite A and B at a moment when A transmits ranging signal can be expressed as

r(t1+τAt)=τAB(t1+τAt)(c+vB)

(7)

Suppose that ranging signal is transmitted att1+τAt, thent1～(t1+τAt) is the transmitting delay. Similarly, the distance between the two satellites at a moment when satellite B transmits ranging signal can be expressed as

r(t2+τBt)=τBA(t2+τBt)(c+vA)

(8)

The relative motion relation of the two satellites is

r(t1+τAt)-r(t2+τBt)=(t2-t1+τBt-τAt)(vA+vB)=

(Δt+τBt-τAt)(vA+vB)

(9)

According to Eqs.(7)-(9), we can obtain

τAB(t1+τAt)(c+vB)-τBA(t2+τBt)(c+vA)=

(Δt+τBt-τAt)(vA+vB)

(10)

Satellite velocity can be accurately calculated by the Doppler frequency shift or by the ephemeris.

τBA(t2+τBt)≠τBA(t2),τAB(t1+τAt)≠τAB(t1),soEqs.(1)(2)cometobe

TA=Δt+τBt+τBA(t2+τBt)+τAr

(11)

TB=-Δt+τAt+τAB(t1+τAt)+τBr

(12)

Synthesizing Eqs.(10)-(12), the final result can be expressed as

(13)

So,thedistanceandtimedifferencebetweenthetwosatellitesatthemomentwhenrangingsignalstransmittedbysatelliteAcan be calculated as

r(t1)=r(t1+τAt)+(vA+vB)τAt=

(14)

(15)

2.2 Analysis of accuracy

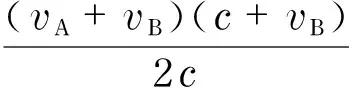
(16)

whereRis the radius of the earth, andhis the orbit altitude. The orbit altitude of LEO satellite ranges from 400 km to 2 000 km. According to Eq. (16), we can obtainv=6.9 km/s-7.7 km/s. In conclusion, the maximum linear velocity of satellite in orbit is 7.7 km/s. So the last two items of the distance error term can be written as

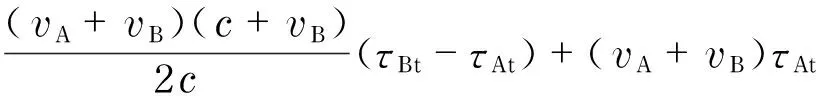
(τBt-τAt)+15.4×103×τAt=

7.7×103×(τBt+τAt)+0.197×(τBt-τAt)

(17)

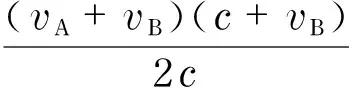
2.57×10-5(τBt-τAt)

(18)

In conclusion, if satellite transmitting delay is in an order of microsecond, which makes (τBt+τAt) larger than 1.3 μs, the last two distance error terms cannot be ignored in Eq.(14) in order to obtain the ranging accuracy of an order of centimeter. Meanwhile, if (τBt-τAt) is larger than 3.89 μs, the time difference error term in Eq.(15) cannot be ignored either in order to attain the precision of an order of 0.1 ns.

3 Simulation and performance analysis

The improved algorithm introduced in this paper is compared with the conventional algorithm demonstrated in Ref. [9]. The improved algorithm considered high-speed motion of satellite during the equipment delay in high dynamic environment. The orbit of Shenzhou-8 is nearly a circular orbit, its perigee height is 334 km, apogee height is 348 km, cycle is about 91 min and velocity is about 7.8 km/s. Simulation parameters are set as such Leo satellites. The simulation results of ranging and time synchronization, utilizing the two algorithms respectively, are shown in Fig.3 to Fig.8. In this paper, three different conditions are considered.

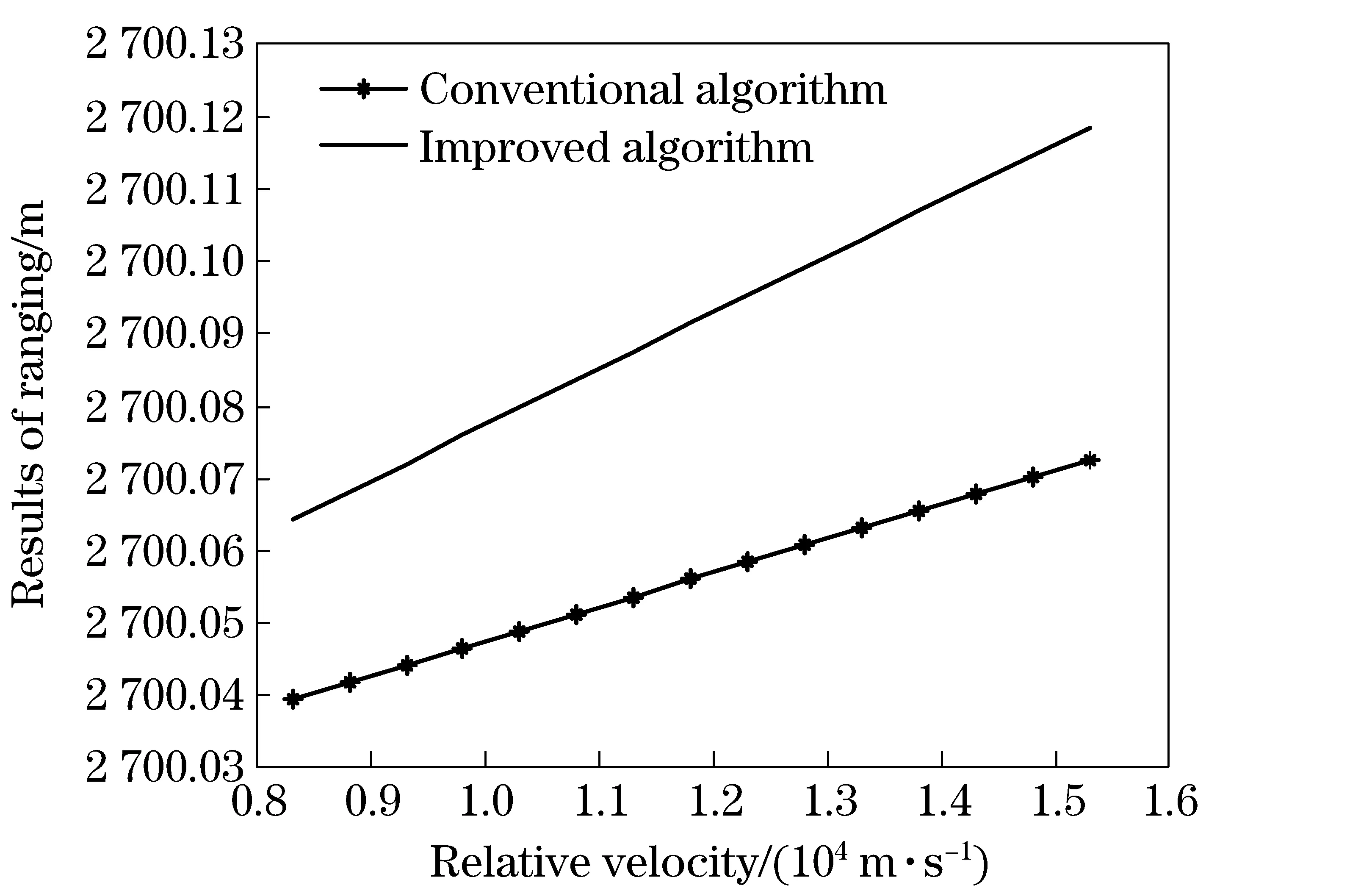
Fig.3 Results of ranging compared the two algorithms under different relative velocity conditions

Fig.4 Results of time difference compared the two algorithms under different relative velocity conditions

Fig.5 Results of ranging compared the two algorithms under different transmitting delay conditions

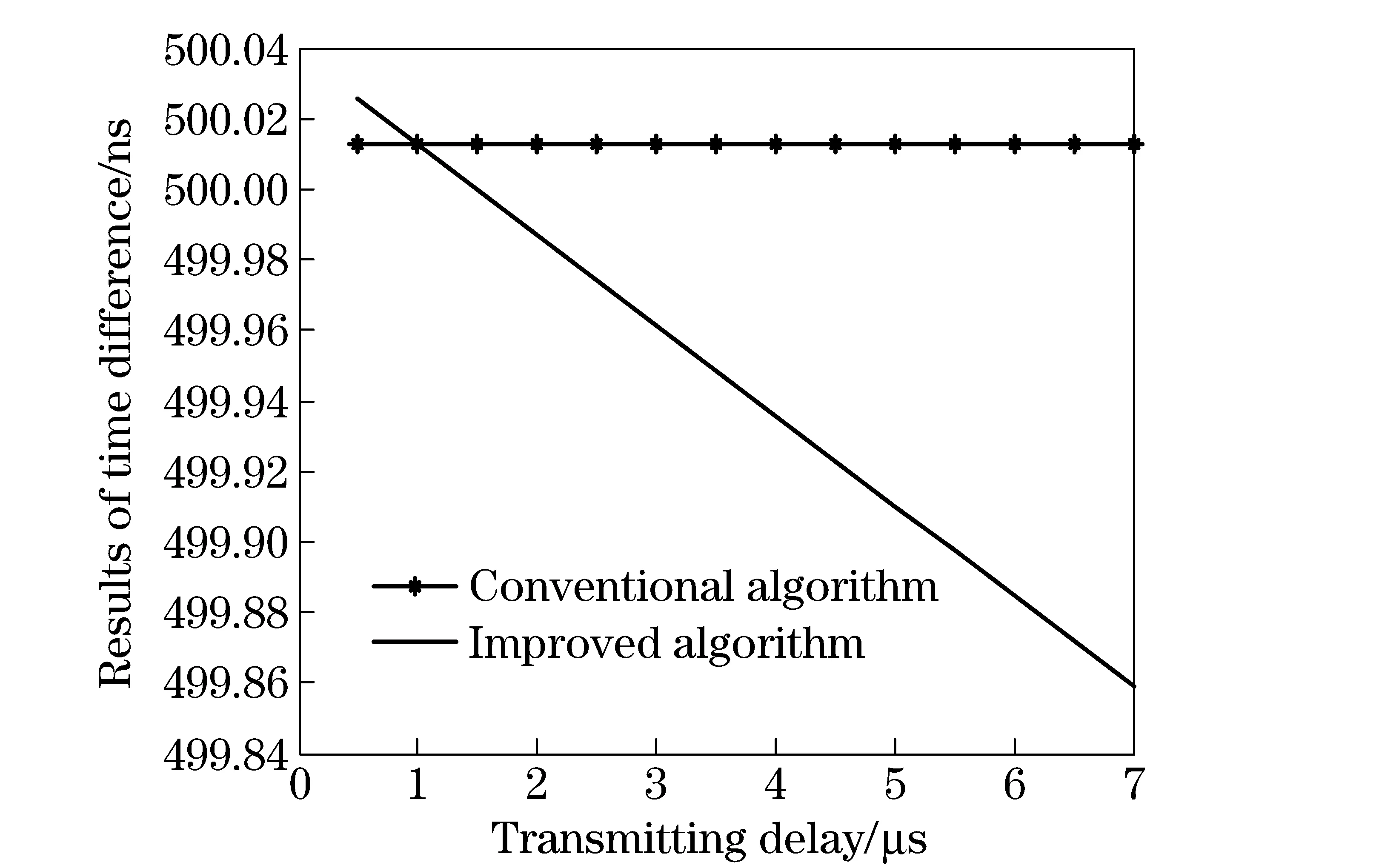
Fig.6 Results of time difference compared the two algorithms under different transmitting delay conditions

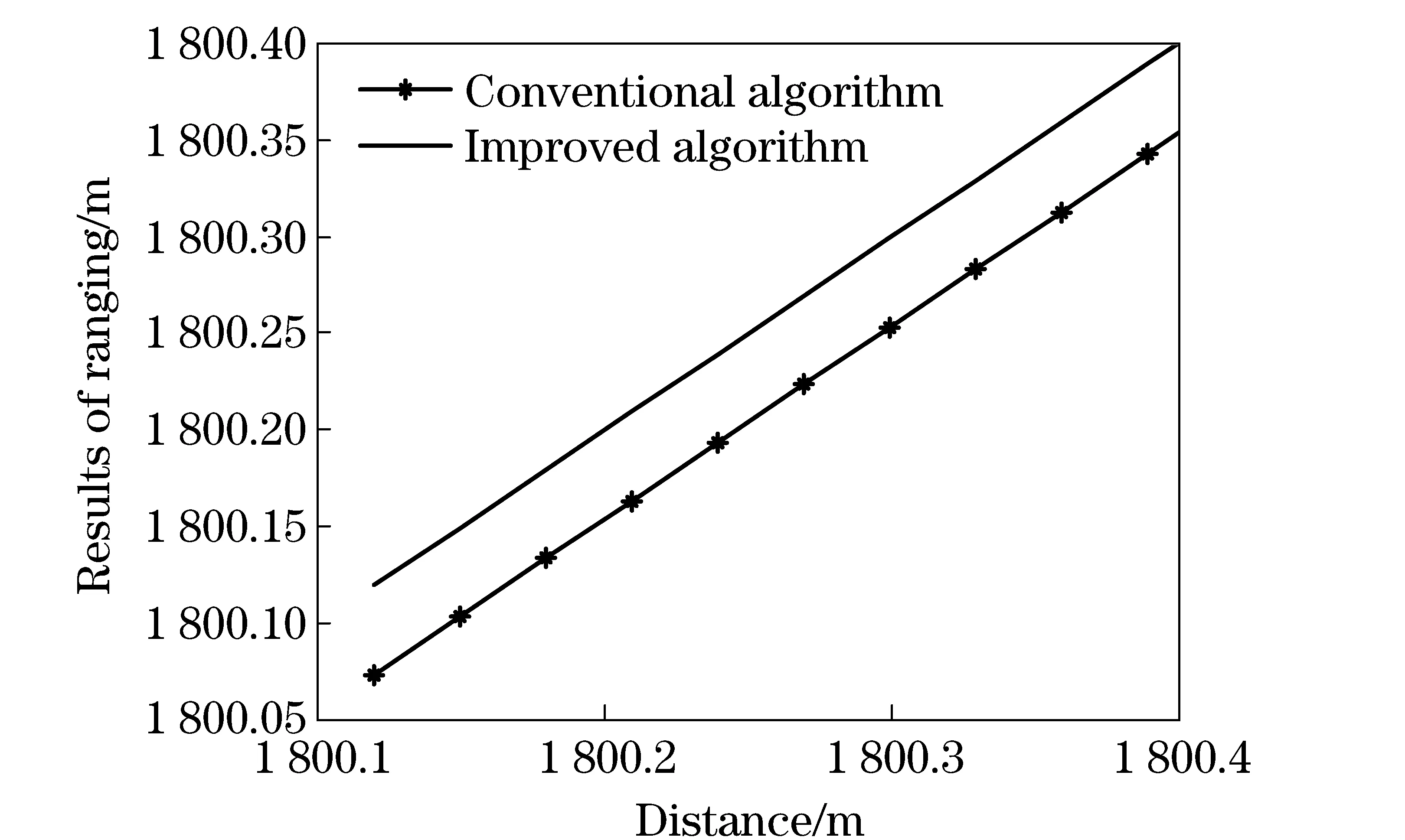
Fig.7 Results of ranging compared the two algorithms under different distance conditions

Fig.8 Results of time difference compared the two algorithms under different distance conditions

① Different relative velocities

Simulation parameters are set as follows: satellite A’s t-r intervalTAis 1.1×10-5s; satellite B’s t-r intervalTBis 1.4×10-5s; satellite A’s transmitting delayτAtis 5×10-6s; satellite B’s transmitting delayτBtis 1×10-6s; satellite A’s receiving delayτAris 5×10-7s; satellite B’s receiving delayτBris 5×10-7s; and relative velocity range between the two satellites is [8 300, 15 400] m/s.

The simulation results show that the error terms in the two algorithms are much larger when the relative velocity between two satellites becomes larger. Compared with conventional algorithm, the new algorithm can correct distance error of 5 cm and time difference error of 0.1 ns at most in dynamic environment. Therefore, the accuracy of inter-satellite ranging and time synchronization is improved in the improved algorithm, which will be more obvious when the relative velocity is larger.

②Different transmitting delays

Simulation parameters are set as follows: satelliteA’s transmitting delayτAtis (5×10-7-7×10-6) s; satellite B’s transmitting delayτBtis 1×10-6s; satellite A’s t-r intervalTAis (τBt+1.1×10-5) s; satellite B’s t-r intervalTBis (τAt+1×10-5) s; satellite A’s receiving delayτAris 5×10-7s; satellite B’s receiving delayτBris 5×10-7s; satellite A’s velocityvAis 7 700 m/s; and satellite B’s velocityvBis 7 700 m/s.

The simulation results show that the error terms in the two algorithms are much larger when the transmitting delay becomes larger. Compared with conventional algorithm, this algorithm can correct distance error of 6 cm and time difference error of 0.16 ns at most in dynamic environment. Therefore, the accuracy of inter-satellite ranging and time synchronization can be improved using the improved algorithm, which is more effective when the transmitting delay is larger.

③ Different distances

Simulation parameters are set as follows: satellite A’s t-r intervalTAis (1.1×10-5-1.100 1×10-5) s; satelliteB’s t-r intervalTBis (TA-3×10-6) s; satellite A’s velocityvAis 7 700 m/s; satellite B’s velocityvBis 7 700 m/s; satellite A’s transmitting delayτAtis 5×10-6s; satellite B’s transmitting delayτBtis 1×10-6s; satellite A’s receiving delayτAris 5×10-7s; and satellite B’s receiving delayτBris 5×10-7s.

The simulation results show that the error term between the improved algorithm and the conventional algorithm is a constant in dynamic environment as the distance of two satellites increases, which means that the error term has nothing to do with the distance factors.

The conclusion is that the new algorithm has obvious advantages compared with the conventional one in high dynamic environment, especially when ranging accuracy of centimeter order and time synchronization accuracy of 0.1 ns are required. The error terms of the two algorithms are mainly affected by relative velocity and satellite transmitting delay, which are much larger when the relative velocity and the transmitting delay becomes larger.

4 Conclusion

In order to eliminate measurement errors caused by high-speed motion of satellite during the transmitting and the receiving delay which are not considered in conventional algorithm, an improved algorithm of inter-satellite ranging and time synchronization, based upon the TWTT theory, is proposed in this paper. The algorithm is deduced on the motion model of two satellites in high dynamic environment and analyzed theoretically. Theoretical analysis demonstrates that the algorithm can effectively enhance the inter-satellite measurement accuracy for ranging systems with centimeter level and time synchronization systems with 0.1 ns level. Finally, simulation results approve the validity of the proposed algorithm by comparing with the conventional algorithm under different conditions. The proposed algorithm is verified to be more effective in high dynamic environment when the satellite transmitting delay and relative velocity become larger.

[1] Chen Zhonggui, Shuai Ping, Qu Guangji. Current satellite navigation system techniques and the development trend analysis [J]．Science in China, 2009, 39(4):686-695. (in Chinese)

[2] Lin Huangtien, Liao Chiashu, Chu Fangdar, et al. Full utilization of TWSTT network data for the short-term stability and uncertainty improvement [J]. IEEE Transactions on Instrumentation and Measurement, 2011, 60(7):2564-2569.

[3] Hanson D W. Fundamentals of two-way time transfer by satellite [C]∥43rdAnnual Symposium on Frequency Control, Denver, Colorado, USA, May31-June 3, 1989.

[4] Merck P, Achkar J. Design of a Ku band delay difference calibration device for TWSTFT station [J]. IEEE Transactions on Instrumentation and Measurement, 2005, 54(2):814-818.

[5] Xu Yong, Chang Qing, Yu Zhijian. On new measurement and communication techniques of GNSS inter-satellite link [J]. Science in China, 2012, 42(2):230-240. (in Chinese)

[6] Koppang P, Wheeler P. Working application of TWSTT for high precision remote synchronization [C]∥The Annual IEEE International Frequency Control Symposium, CA, USA, May 27-29, 1998

[7] Li Zhigang, Qiao Rongchuan, Feng Chugang.Two way satellite time transfer(TWSTT) and satellite ranging [J]. Journal of Spacecraft TT&C Technology, 2006, 25(3):1-6. (in Chinese)

[8] Zhong Xingwang, Chen Hao. The system and its calibration method on inter-satellite dual one-way ranging and timing [J]. Journal of Electronic Measurement and Instrument, 2009, 23(4):13-17. (in Chinese)

[9] Huang Bo, Hu Xiulin. Inter-satellite ranging and time synchronization technique for BD2 [J]. Journal of Astronautics, 2011, 32(6):1271-1275. (in Chinese)

[10] Zhong Xingwang, Chen Hao. Analysis and correction techniques of movement influence on inter-satellite two-way time transfer [J]. Chinese Space Science and Technology, 2007(6):54-58. (in Chinese)

(Edited by Cai Jianying)

10.15918/j.jbit1004- 0579.201524.0215

TN 927.3; V448.2 Document code: A Article ID: 1004- 0579(2015)02- 0233- 07

Received 2013- 12- 07

Supported by the National High Technology Research and Development Program of China (2012AA1406)

E-mail: wangyongqing@bit.edu.cn