Efficient and fair resource allocation in downlink OFDMA systems
2015-04-22SONGZhengyu宋政育HOUShujuan侯舒娟WUSiliang吴嗣亮
SONG Zheng-yu(宋政育), HOU Shu-juan(侯舒娟), WU Si-liang(吴嗣亮)
(School of Information and Electronics, Beijing Institute of Technology, Beijing 100081, China)
Efficient and fair resource allocation in downlink OFDMA systems
SONG Zheng-yu(宋政育), HOU Shu-juan(侯舒娟), WU Si-liang(吴嗣亮)
(School of Information and Electronics, Beijing Institute of Technology, Beijing 100081, China)
A resource allocation problem considering both efficiency and fairness in orthogonal frequency division multiple access (OFDMA) systems is studied. According to the optimality conditions, a downlink resource allocation algorithm consisting of subcarrier assignment and power allocation is proposed. By adjusting the tradeoff coefficient, the proposed algorithm can achieve different levels of compromise between efficiency and fairness. The well-known classic resource allocation policies such as sum-rate maximization algorithm, proportional fairness algorithm and max-min algorithm are all special cases of the proposed algorithm. Simulation results show that the compromise between efficiency and fairness can be continuously adjusted according to system requirements.
orthogonal frequency division multiple access (OFDMA); resource allocation; downlink; efficiency; fairness
To satisfy the ever-growing requirements of high-data-rate services, orthogonal frequency division multiple access (OFDMA) has been selected as the multiplex and multiple access scheme by some state-of-the-art wireless systems such as LTE and WiMAX. For OFDMA systems, radio resource management plays an essential role in completely fulfilling the physical layer’s potential to support a large number of users with various channel conditions and quality-of-service (QoS) requirements.
Efficiency and fairness are the most crucial but conflicting performance metrics in radio resource management. To maintain certain degree of fairness, the users with bad channel conditions will consume more radio resources, and accordingly, reduce the system’s spectrum efficiency. A downlink sum-rate maximization algorithm was proposed in Ref. [1], which reaches the maximum spectrum efficiency, however, without any consideration of user fairness. In Refs. [2-3], the max-min and modified max-min algorithm were investigated. The max-min algorithm maximizes the minimum user’s data rate to guarantee absolute user fairness, but the efficiency is extremely low. Many researchers have studied the tradeoff between efficiency and fairness from variable points of view[4-10]. In Ref. [4], the proportional fairness (PF) scheduler is extended from Qualcomm’s HDR to multicarrier transmission systems like OFDMA. In Refs. [5-6], the simulation results show that PF algorithm provides a good tradeoff between efficiency and fairness. In Refs. [7-8], it is pointed out that some appropriately designed utility functions, usually increasing functions with a decreasing slope, can effectively balance the efficiency and fairness. In Refs. [9-10], several sum-rate maximization algorithms with fairness consideration are designed to provide some degree of fairness.
In this paper, we propose a unified resource allocation algorithm with tradeoff coefficient for OFDMA downlink, which can achieve different levels of tradeoff between efficiency and fairness. By adjusting the tradeoff coefficient, the network operators can operate the system according to the requirements of variable cells or one cell at different times. The sum-rate maximization algorithm, proportional fairness (PF) algorithm and max-min algorithm are all special cases of it.
1 Problem formulation
Consider a single-cell downlink OFDMA system withMusers,Nsubcarriers and total bandwidthB. Each user witnesses different fading levels on each subcarrier. Denote the transmit power, channel gain and noise power of usermon subcarriernaspm,n,Hm,nand σm,n,respectively.AccordingtoShanonchannelcapacityformulaandconsideringpracticalmodulationscheme,thedatarateofusermonsubcarriernisgivenby
(1)
whereβmistheSNRgapofuserm[11].IfQAMschemeisapplied, βm=-ln(5Pe)/1.5,wherePeisthetargetbiterrorrate.
Consequently,thetotaldatarateofusermis
(2)
whereρm,nisthesubcarrierallocationindex.Ifsubcarriernisallocatedtouserm, ρm,n=1;otherwise, ρm,n=0.
AresourceallocationoptimizationproblemtakingaccountofbothefficiencyandfairnessindownlinkOFDMAsystemscanbeexpressedas
(3)

(4)
pm,n≥0, for ∀mand ∀n
(5)
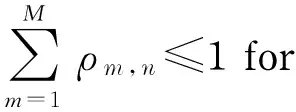
(6)
ρm,n=0 or 1
(7)
where θisthetradeoffcoefficientandPTisthetotaldownlinktransmitpower.TheconstraintsofEqs.(6)(7)meaneachsubcarrierisexclusivelyallocatedtoonesingleuser.
2 Optimality conditions
Eq.(3)isanonlinearintegerprogrammingproblemwithprohibitivelyhighcomplexityofO(MN).WefollowRef.[12]torelaxρm,ntobearealnumberin[0,1]toreducethecomplexity,andthenEq. (3)istranslatedintoaconvexoptimizationproblem[13].TheLagrangianassociatedwiththeconvexoptimizationproblemis
(8)
whereλandνnarethenon-negativeLagrangianmultipliersvectors.Accordingly,theKKToptimalityconditionsareobtainedas
(9)
(10)
(11)
(12)

According to the convex optimization theory, when the primal problem is convex, the KKT conditions are not only necessary but also sufficient for the point to be the globally optimal solution. Therefore, the optimal resource allocation algorithm can be derived from Eqs.(9)-(12).
(13)
Likewise,fromEqs. (10)(12),thepowerallocatedtouserm*on subcarriernsatisfies
(14)
AccordingtotheconclusioninRef.[14],Eq. (3)stillhasanoptimalsolutionwhenρm,ntakethevalueofeither0or1.Thus,wetakeρm*,n=1andEq.(14)istranslatedinto
(15)
Noticethatpm*,n≥0, then the power allocated to userm*on subcarriernis
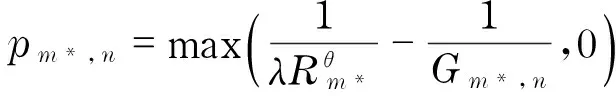
(16)
whichisthefashionofwater-fillingpowerallocationamongthesubcarrierswithinuserm*.Lm*is the water-level of userm*.
In summary, Eqs.(13)(16) consist of the optimal criteria to allocate the subcarriers and transmit power.
In particular, when θ=0,Eq.(3)isjusttheobjectivefunctionofsum-ratemaximizationalgorithm.Whenθ→+∞,ifRm* (17) Eqs.(13)(16) are closely coupled with each other. To reduce the complexity, we propose a practical suboptimal resource allocation algorithm to decouple them via two separate steps: subcarrier assignment for users and power allocation among subcarriers within one user. Firstly, we assume equal power allocation over all downlink subcarriers to make Eq.(13) more tractable. That is pm,n=PT/N (18) Then, Eq. (13) is applied to allocate subcarriers to users. At each decision epoch, if assuming subcarriernis allocated to userm, the data rate of usermis updated by Rm(t)=Rm(t-1)+rm,n (19) whereRm(t) is userm’s data rate at the timet. At last, after the subcarrier allocation, power allocation is conducted among the subcarriers within one user. With the previous equal power allocation assumption, the total power allocated to usermis Pm=|Ψm|PT/N (20) where Ψmisthesubcarriersetassignedtousermand|Ψm|isthecardinalityofΨm.Foruserm,thewater-fillinglevelis (21) Then,Eq. (16)isusedtoimplementthewater-fillingpowerallocationamongthesubcarrierswithinoneuser. Insummary,theproposedjointsubcarrierandpowerallocationalgorithmisgivenasfollows. Step 1 Initialization. Let Ψm=∅, Rm=0, Lm=0for∀mandthesetofsubcarriersΨ={1,2,…,N}. Step 2 Allocate each user only one subcarrier that has the best SNR for that user. Form=1 toM, ρm,n*=1; Ψm=Ψm∪{n*},Ψ=Ψ-{n*}; Rm=Rm+rm,n*; End for. Step3Assigntheremainingsubcarrierstouserm*accordingtoEq. (12). WhileΨ≠∅, form=1 toM, End for. ρm*,n(m*)=1; Ψm*=Ψm*∪{n(m*)},Ψ=Ψ-{n(m*)}; Rm*=Rm*+rm*,n(m*); End while. Step4Powerallocation. In the simulations, a single-cell environment with the radius of 1km is considered. Without loss of generality, letβm=1 for all users. Suppose there are 1 024 subcarriers. The total noise power is -100 dB and the BS maximum transmit power is 10 W. The modified Hata urban propagation model in Ref.[15] is adopted to describe the large-scale propagation loss. Besides, the shadow fading follows lognormal distribution with mean value of 0 dB and standard deviation of 8 dB. We get the average values of efficiency and fairness from 10 000 trials. The user fairness is quantitatively measured by Jain’s fairness index (FI)[15] (22) ThevalueofFis bounded in the interval of (0, 1]. IfF=1, it means all users get the same data rate and the system is 100% fair. As the disparity increases,Fdecreases to 0. Figs.1-3 demonstrate the spectrum efficiency and user fairness with respect to the tradeoff coefficient θwhenthenumberofusersis25, 50and100,respectively.Itcanbeseenfromthetwofiguresthatasθincreases,thespectrumefficiencydecreasescontinuouslyfromthehighestpoint,whileuserfairness,intermsoffairnessindex,experiencesanupwardtrendtoalmost1.Therefore,thetradeoffbetweenefficiencyandfairnesscanbecontinuouslyadjustedthroughthecoefficientθaccordingtothesystemrequirements.Inaddition,duetothemultiuserdiversity(MUD)gain,theefficiencywithM=100ismorethanthatwithM=50,anditisalsothecasewithM=50andM=25. Fig.1 Spectrum efficiency and user fairness vs. the tradeoff coefficient θ with M=25 Fig.2 Spectrum efficiency and user fairness vs. the tradeoff coefficient θ with M=50 Fig.3 Spectrum efficiency and user fairness vs. the tradeoff coefficient θ with M=100 Moreover,astheanalysisabove,whenθ=0,itisthecaseofsum-ratemaximizationalgorithm,whichhasthemaximumspectrumefficiencyandtheworstfairnessindex.Whenθ→1,itisthePFalgorithmwithbothefficiencyandfairnessrelativelyhighinthetwofigures.ItmeansPFalgorithmcanachieveagoodtradeoffbetweenefficiencyandfairness,whichisoneofthereasonswhythePFalgorithmiswidelyused.Additionally,fromthesethreefigures,itcanbeexpectedthatwhenθ→+∞, Fisalmost1,butthethroughputwilldeclinetoamuchlowerlevel,whichisthecaseofmax-minalgorithm. Inthispaper,weformulatearesourceallocationproblemfortheOFDMAdownlink.ThenKKToptimalityconditionsarederived,accordingtowhichajointsubcarrierandpowerallocationalgorithmisproposed.Theproposedalgorithmcanachievedifferentlevelsofcompromisebetweenefficiencyandfairnessbyadjustingthetradeoffcoefficientθ.Itcanworkastheclassicsum-ratemaximizationalgorithm,PFalgorithmandmax-minalgorithmwhenθ=0, θ→+∞andθ→1,respectively.Besides,simulationresultsalsoshowthatthecompromisecanbecontinuouslyadjustedtosatisfythesystemrequirements. [1] Jang J, Lee K B. Transmit power adaptation for multiuser OFDM systems [J]. IEEE Journal on Selected Areas in Communications, 2003, 21(2): 171-178. [2] Rhee W, Cioffi J M. Increasing in capacity of multiuser OFDM system using dynamic subchannel allocation [C]∥Proceedings of IEEE 51st Vehicular Technology Conference, Tokyo, Japan, 2000. [3] Shen Z, Andrews J G, Evans B L. Adaptive resource allocation in multiuser OFDM systems with proportional rate constraints [J]. IEEE Transactions on Wireless Communications, 2005, 4(6): 2726-2737. [4] Kim H, Han Y. A proportional fair scheduling for multicarrier transmission systems [J]. IEEE Communications Letters, 2005, 9(3): 210-212. [5] Nguyen T D, Han Y. A proportional fairness algorithm with QoS provision in downlink OFDMA systems [J]. IEEE Communications Letters, 2006, 10(11): 760-762. [6] Fraimis I G, Kotsopoulos S A. QoS-based proportional fair allocation algorithm for OFDMA wireless cellular systems [J]. IEEE Communications Letters, 2011, 15(10): 1091-1093. [7] Song G C, Li Y G. Cross-layer optimization for OFDM wireless networks-part I: theoretical framework [J]. IEEE Transactions on Wireless Communications, 2005, 4(2): 614-624. [8] Song G C, Li Y G. Cross-layer optimization for OFDM wireless networks-part II: algorithm development [J]. IEEE Transactions on Wireless Communications, 2005, 4(2): 625-634. [9] Ma Y, Kim D I. Rate-maximization scheduling schemes for uplink OFDMA [J]. IEEE Transactions on Wireless Communications, 2009, 8(6): 3193-3205. [10] Leith A, Alouini M S, Kim D I, et al. Flexible proportional-rate scheduling for OFDMA system [J]. IEEE Transactions on Mobile Computing, 2013, 12(10): 1907-1919. [11] Qiu X X, Chawla K. On the performance of adaptive modulation in cellular systems [J]. IEEE Transactions on Communications, 1999, 47(6): 884-895. [12] Wong C Y, Cheng R S, Letaief K B, et al. Multiuser OFDM with adaptive subcarrier, bit and power allocation [J]. IEEE J Select Areas Commun, 1999, 17(10): 1747-1758. [13] Boyd S, Vandenberghe L. Convex optimization [M]. Cambridge: Cambridge University Press, 2004. [14] Kim K, Han Y, Kim S L. Joint subcarrier and power allocation in uplink OFDMA systems [J]. IEEE Communications Letters, 2005, 9(6): 526-528. [15] Hata M. Empirical formula for propagation loss in land mobile radio services [J]. IEEE Transactions on Vehicular Technology, 1980, 29(3): 317-325. (Edited by Cai Jianying) 10.15918/j.jbit1004- 0579.201524.0213 TN 929.52 Document code: A Article ID: 1004- 0579(2015)02- 0222- 05 Received 2013- 12- 06 E-mail: shujuanhou@bit.edu.cn
3 Proposed resource allocation algorithm

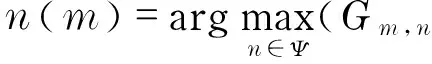
4 Simulation results



5 Conclusion
杂志排行
Journal of Beijing Institute of Technology的其它文章
- Numerical simulation of effects of operating conditions on the molecular weight of polypropylene using a response surface method
- Effect of cutting speed on residual stress of special coating during remanufacturing
- Un-powered gliding aircraft’s ballistic missile optimal design
- Quantification of CP4-EPSPS in genetically modifiedNicotianatabacum leaves by LC-MS/MS with 18O-labeling
- Investigation on experimental method of low-impedance materials using modified Hopkinson pressure bar
- Effect of solvent on the crystal morphology of royal demolition explosive
