Analysis of stress-magnetic coupling effect in weak magnetic environment

QIU Zhong-chao(邱忠超), ZHANG Wei-min(张卫民) GUO Yan(果艳)DUBOV A A

(1.School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China;2.Energodiagnostika Company, Moscow 143965, Russia)



Analysis of stress-magnetic coupling effect in weak magnetic environment

QIU Zhong-chao(邱忠超), ZHANG Wei-min(张卫民)1, GUO Yan(果艳)1,DUBOV A A2

(1.School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China;2.Energodiagnostika Company, Moscow 143965, Russia)

Metal magnetic memory (MMM) signals are difficult to be analyzed due to noise interference, which limits its practical engineering application. A method of improving the magnetic signals is proposed in this paper by placing the excitation device which generates a weak external magnetic field about 100 A/m. The effect of the external magnetic field on the magnetic signals is studied using both finite element method (FEM) and uniaxial tensile tests. Comparison of the test data with the simulation ones of stress-magnetic coupling shows that the magnetic signals are strengthened and the measurement sensitivity of the detection system is greatly improved through the external magnetic excitation. Moreover, the FEM result has a good agreement with the testing results of No.20 steel plate. The proposed method has laid a foundation for further practical engineering application.

stress-magnetic coupling; metal magnetic memory; stress concentration; finite element analysis; measurement sensitivity

Ferromagnetic materials are widely used in fields like aerospace, railway, pressure vessel and petroleum for their beneficial mechanical properties. In order to control the quality of ferromagnets, it is important to timely monitor the damage state and to predict their residual life. Components can be removed from service before there is any likelihood of failure in case catastrophic accidents occur.

Conventional nondestructive testing techniques, such as ultrasonic test, eddy current inspection and penetrate inspection, are effective in assessing existing defects, but unsuitable for potential damage and early stress concentration zone. The situation had not been changed until metal magnetic memory (MMM) testing was proposed in Russia in the late 1990s[1]. In stress concentration zone, the tangential component of magnetic field,Hp(x), has a maximum value, meanwhile, the normal component,Hp(y), changes positive-negative and has a zero value.

The physical mechanism of the MMM effect, however, is still unclear due to lack of deeper theoretical support. Furthermore, the magnetic signals measured usually contain some interfering factors, for instance, the difference of demagnetizing field, microstructure distribution and heat treatment condition, leading to a serious distortion of test results and hence invalid conclusions[2-3].

MMM signals are susceptible to the environmental factors and difficult to truly reflect the variation of stress. To solve the problem, we propose that MMM signals can be strengthened by the external magnetic excitation, reducing the interference of the environmental factors and improving the sensitivity of the detection system. The basic principle of this method is discussed and the concept of the measurement sensitivity of the MMM detection system is proposed. Stress-magnetic coupling simulation of No.20 steel specimens in static tensile testing is analyzed and the surface magnetic signals distribution is obtained. The static tensile tests in an external magnetic environment are conducted. The results show that the external magnetic excitation can suppress noise interference validly and improve the sensitivity of detection system significantly.

1 Sensitivity analysis of detection system

MMM effect is a magneto-mechanical effect under geomagnetic field. Generally, magneto-mechanical effect refers to a series of changes of magnetic properties of ferromagnetic materials, resulting from the variation of applied stress at a constant magnetic field.

Based on the concepts of “effective field theory” and “law of approach”, the Jiles-Atherton-Sablik model for magneto-mechanical effect was presented by Jiles et al[4-5]. The magnetization caused by applied stressσis equivalent to a magnetic fieldHσfor a macroscopic polycrystalline multi-domain system:

(1)

whereλ,μ0andMare the bulk magnetostriction constant, vacuum permeability and the magnetization, respectively.

It is implicit that the magnetization under applied fieldHand stressσis identical to an equivalent effective magnetic fieldHeσ, that is

Heσ=H+αM+Hσ

(2)

whereαis the strength of the coupling of the individual magnetic moment to the magnetizationM.

Thus, we can propose the sensitivityKof detection system,

(3)

whereHe0is the initial magnetic field before testing,σ0is the initial residual stress before the tests.

The sensitivity of the stress measurement system refers to the variation of surface magnetic field intensity caused by unit stress. Comparing the sensitivity of different testing conditions, the best testing parameters can be obtained.

2 Simulation of stress-magnetic coupling

2.1 Stress-magnetic coupling based on stress-permeability model

MMM effect refers to the abnormal changes of the surface magnetic field due to uneven stress distribution within ferromagnetic material in geomagnetic environment. Indeed, MMM effect, which has not reached conclusion uniformly, is stress-magnetic coupling effect[6-7].

Stress-magnetic coupling effect, as a fundamental characteristic of ferromagnetic materials, refers to stress-induced permeability variation, thereby leads to the variation of the surface magnetic intensity of the ferromagnetic materials[8-10]. From the perspective of micro-mechanism, ferromagnetic materials are composed of numerous magnetic domains. Every domain is of the order of 10-8-10-12m3in volume and consists of 1012-1015atoms. The magnetic moments distribute randomly in initial state and no magnetization appears. When a ferromagnetic specimen is loaded in external magnetic field, a tension causes the domains in the direction of the applied load for the positive magnetorestrictive materials, whereas a compression orients the domains to be perpendicular to the loading direction due to the piezomagnetic effect. The macroscopic parameters of ferromagnetic specimen, such as permeabilityμ, would change along with the magnetic moment rotation and the magnetic domain-wall displacement[11-13].

The permeability of ferromagnetic materials is not constant, but shows complex variation when they are placed in different external magnetic fields and loadings. According to the relevant reference, whenHis less than 640 A/m, it is far from saturation magnetization and belongs to a range of weak magnetic excitation. The permeability decreases sharply whileHincreases from 640 A/m to 8 000 A/m, but it is approximately unchanged for being close to saturated magnetization whenHis more than 8 000 A/m[14].

According to previous research[15], when ferromagnetic component is affected by a weak magnetic field and uniaxial stress as

μ=μTf(H)g(σ)=μT(1+bH/μT)[a0+a1|σ|mexp(n|σ|)]

(4)

whereμTis the initial magnetic permeability relating to temperatureT,bis a constant relating to material properties;a0,a1,m,nare the coefficients depending on the direction and value of the applied stress.

In the geomagnetic field environment withμT=285,b=2.5 andH=40 A/m, according to the relationship between tensile permeability and stress of No.20 steel under stress coaxial in geomagnetic field, the corresponding parameters can be obtained by the least squares fitting firstly and then quadratic optimization :a0=0.071 3；a1=0.041 5；m=1.542 5；n=-0.031 5.

μ=27.412+15.977 5σ1.542 5e-0.031 5σ

(5)

In the same way, when specimen is placed under external magnetic field about 100 A/m, we can obtain

μ=42.78+24.9σ1.542 5e-0.031 5σ

(6)

Eq.(5) and Eq.(6) are the dependence of permeability on stress in different magnetic environment, and laid a foundation for stress-magnetic coupling effect quantitatively.

2.2 Simulation of stress-magnetic coupling

Magnetic finite element method (FEM) is a powerful tool for the investigation of the magnetic signals due to its flexibility for simulating irregular structures. The FEM of stress-magnetic coupling effect refers to the surface magnetic field distribution in different magnetic environments and the loads in the region of No.20 steel and the air layer around the specimen. The dependence of stress on the magnetic signals is the predominant role in stress-magnetic coupling while the dependence of magnetic field on stress is negligible, so the FEM is conducted by using the indirect method, which is more rational and efficient. The simulation procedure is shown in Fig.1.

Fig.1 Simulation procedure of stress-magnetic coupling effect

Simulation has mainly two steps: static analysis and static magnetic analysis. Static analysis can acquire stress distribution results of the loading model. In the static magnetic analysis, magnetic properties of ferromagnetic specimen element are assigned firstly by the static analysis results, and then the static magnetic analysis is done and the surface magnetic field distribution can be obtained subsequently.

Taking No.20 steel plate as the research object, the sizes and main technical parameters are shown in Fig.2 and Tab.1. The thickness of the specimen is 4 mm.

Fig.2 Geometry of specimen

Tab.1 Main parameters of 20#steel

Elasticmodulus/GPaPoisson’sratioYieldstress/MPa2030 28240

The finite element model is established firstly. Due to the fact there is magnetic flux leakage in the air around the specimen, the air model around the specimen should be established. Accordingly, the 3D model of the specimen and the air around it is established with the help of the ANSYS software, as shown in Fig.3. The inner is the specimen model while the outer is air model. Hard points are established in advance for extracting the surface magnetic field in the process of the general postproc of ANSYS.

Fig.3 Whole 3D model of stress-magnetic coupling

The model is meshed by the combination of automatic and manual methods. The middle region of the specimen model and the air layer around the specimen need to be subdivided to ensure the accuracy, while the region far from the specimen can be divided relatively rough, as shown in Fig.4. In static analysis, the model of symmetry side is applied with displacement constraints and two sides are loaded, with the displacement constraints and loads automatically translated to the corresponding nodes. The stress distribution under 8 kN loading is shown in Fig.5.

Fig.4 Finite element mode of specimen

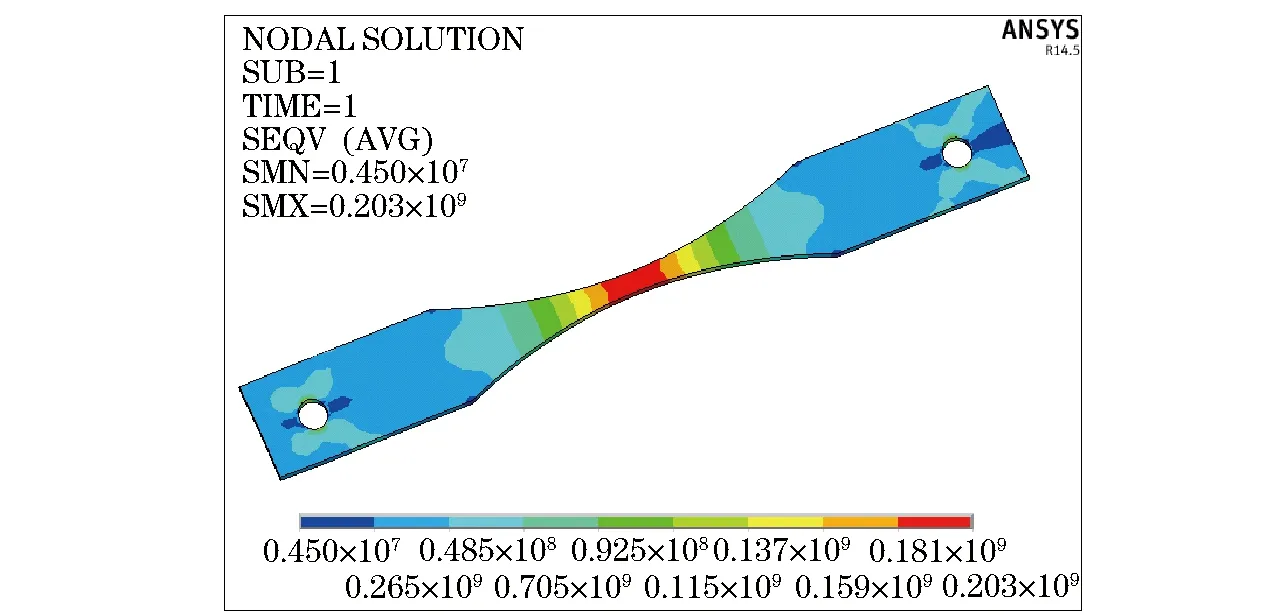
Fig.5 Stress distribution under 8 kN loading

Stress distribution is exported after static analysis and magnetic properties are assigned subsequently. In static magnetic analysis, solid236 element is used, which is a 3D-20node element capable of modeling electromagnetic fields. The static magnetic analysis is conducted in different magnetic environments (40 A/m and 100 A/m). At last, the entire model is solved and post-processed.

2.3 Simulation results and analysis

Fig.6 shows the surface magnetic field distribution of the specimen under 8 kN loading in geomagnetic environment. The simulation results of stress-magnetic coupling effect based on the stress-permeability model agree well with the basic theory of MMM which indicates that this model can better explain the phenomenon of MM.

Fig.6 Surface magnetic field distribution under 8 KN applied stress

The dependence of the measurement sensitivity of the detection system on the magnetic environment is analyzed with ANSYS. Two weak magnetic environments, the geomagnetic filedH1=40 A/m and the external magnetic fieldH2=100 A/m, are chosen for numerical simulation. The magnetic intensity of the center of the specimen surface in different magnetic environments can be obtained and analyzed, and the sensitivityKin different magnetic environments can be analyzed in terms of the concept of sensitivity mentioned, as shown in Tab.2.

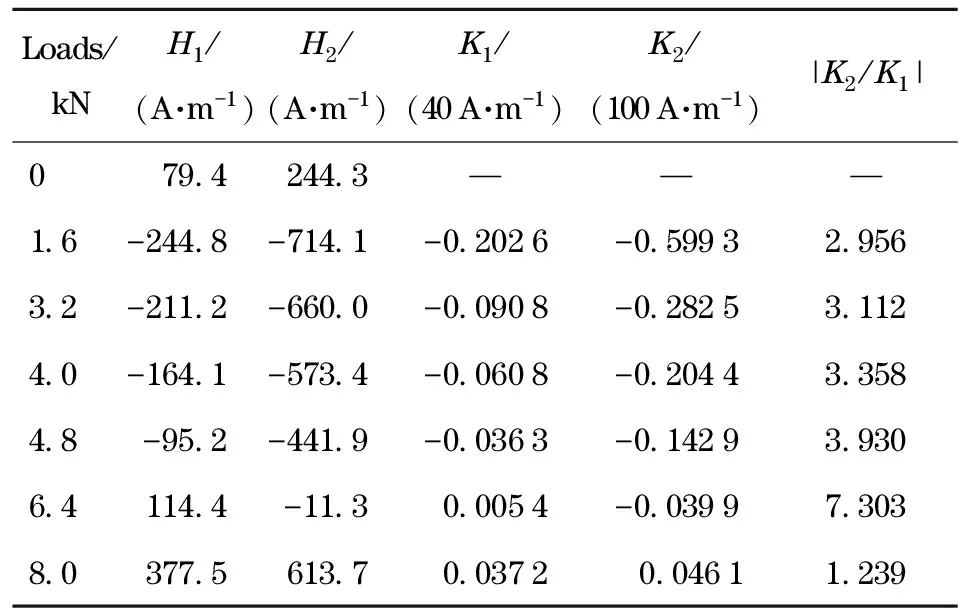
Tab.2 Measurement sensitivity in different loads and magnetic field environment

Tab.2 shows the measurement sensitivity in different loads and magnetic environments. The sensitivity of the detection system can be improved significantly due to the external magnetic excitation. This indicates the magnetic signals can be strengthened by applying an external magnetic excitation appropriately, improving the measurement sensitivity and the reliability of the MMM detection system in practical engineering application.

3 Experiment

3.1 Experimental material and method

The test specimen is shown in Fig.2. The static tensile tests were performed with a home-made testing machine, whose load error is within ±0.5%. Twenty-one points at intervals of 5 mm were marked on the surface of the sample before testing, which were named point 1, point 2, … , and point 21 in sequence from left to right. Fig.7 shows the whole stress measurement system. In the tensile testing, the specimen was firstly loaded to a predetermined stress, and the normal components of the surface magnetic field, ΔHp(y), were immediately measured by a magnetic indicator TSC-1M-4 with a scanning sensor type 2. Subsequently, the ΔHp(y) values of the measured points were collected and analyzed offline. After that, the specimen was loaded again to a higher predetermined stress and the above procedures were repeated until the phenomenon of yielding occurred. The magnetic signal was measured from top to bottom in-situ while the specimen was under load.

Fig.7 Stress measurement system by magnetic testing method

3.2 Experimental results and analysis

The characteristics of the surface magnetic signals of every specimen are not identical, while their overall trends are consistent. In this paper, one representative signal is taken for analysis. In order to eliminate the magnetic field interference produced by the two ferromagnetic clamps, the magnetic signal variation, ΔHp(y) that equals theHp(y) component under loading minus theHp(y) component after clamping but before loading, was investigated. Fig.8 shows the dependence of the magnetic signals of the 21 measurement points on the specimen surface on loads under different weak magnetic environments.

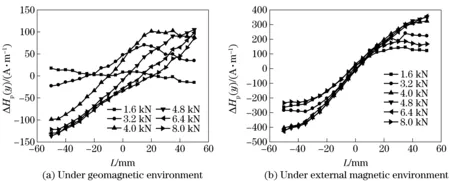
Fig.8 ΔHp(y) components of 21 points under different loads

In geomagnetic environment, the normal components, ΔHp(y) values, are unstable and uneven. Besides, the crossing zero position which ranges from -20 mm to 20 mm is different obviously, so it is difficult to evaluate stress concentration zone effectively. However, ΔHp(y) values increase and show a regularity obviously when the specimens are subjected to an external magnetic field. And the zero position located in -3 mm-2 mm, which agrees well with the stress concentration zone of the specimens.

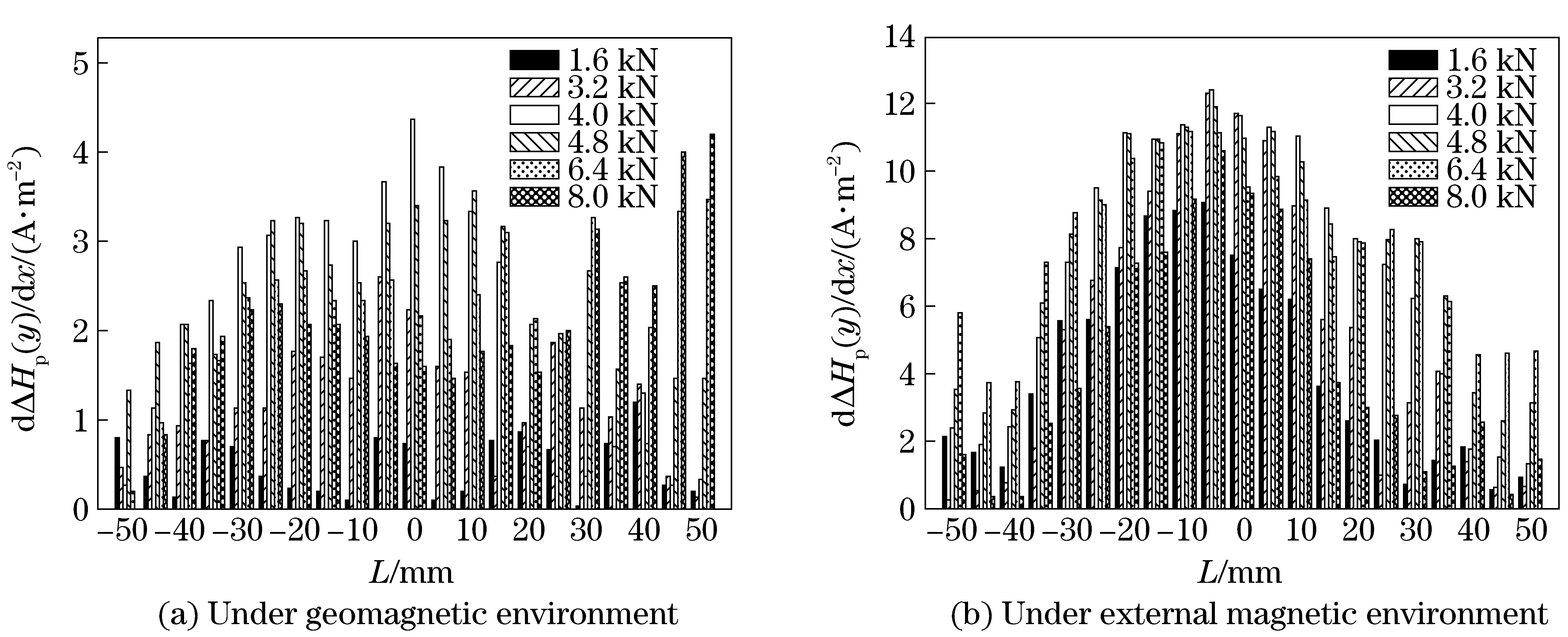
Fig.9 dΔHp(y)/dx components of 21 measurement points under different loads

Fig.9 shows the dependence of the magnetic signals gradient dΔHp(y)/dxof the 21 measurement points on the specimen surface on loads in different magnetic environments. From the two graphs in Fig.9, the magnetic signals gradient, dΔHp(y)/dx, look like disorderly and has different variations, which is unfavorable for analyzing its characteristics and trends. When applying an external magnetic field instead of geomagnetic field as the stimulus, the magnetic signals gradients, dΔHp(y)/dx, increase significantly and show variation trend uniformly. Additionally, the maximum gradient values locate in -5 mm or 0, which shows a good agreement with the stress concentration zone of the specimens.

For magnetic signals in geomagnetic environment, the normal component of magnetic signals are all in a mess due to the magnetic field generated by the clamps and other interference noise, which is unfavorable to analyze the signal characteristics and trend. While applying an external magnetic field, the magnetic signals can be strengthened and the trend of magnetic signals is clear, which is favorable to find stress concentration zone and improve the sensitivity of the detection system significantly.

4 Conclusions

① The No.20 steel was the research object. The stress-magnetic coupling was simulated based on stress-permeability model. Through the static analysis and the static magnetic analysis, the normal component distribution of the magnetic field intensity agrees well with the basic theory of MMM, which further validates that this model can explain the MMM phenomenon well.

② The measurement sensitivity of the detection system in different weak magnetic environments is analyzed with ANSYS, and the results show that the sensitivity can be improved significantly in an external magnetic environment.

③ The static tensile test is conducted on the No.20 steel in different weak magnetic environments and the results have a good agreement with the FEM results, reconfirming that the magnetic signals can be strengthened and the sensitivity of the detection system can be improved by applying the external magnetic excitation. The research lays a foundation for practical engineering application of the MMM technique.

[1] Dubov A A. A study of metal properties using the method of magnetic memory [J]. Metal Science Heat Treat, 1997, 39(9/10):401-405.

[2] Leng Jiancheng, Xu Minqiang, Zhang Jiazhong. Application of empirical mode decomposition in early diagnosis of magnetic memory signal [J]. Journal of Central South University of Technology, 2010, 17:549-553.

[3] Leng Jiancheng, Xu Minqiang, Zhou Guoqiang, et al. Effect of initial remanent states on the variation of magnetic memory signals [J]. NDT&E International, 2012, 52:23-27.

[4] Jelie D C. Theory of the magneto-mechanical effect [J]. Journal of Physics D: Applied Physics, 1995, 28(8):1537-1546.

[5] Li Lu, Jiles D C. Modified law of approach for the magneto-mechanical model: application of the Rayleigh law to stress [J]. IEEE Transactions on Magnetics, 2003, 39(5):3037-3039.

[6] Yang En, Li Luming, Chen Xing. Magnetic field aberration induced by cycle stress [J]. Journal of Magnetism and Magnetic Materials, 2007, 312(1):72-77.

[7] Wang Zhengdao, Yao Kai, Deng Bo, et al. Quantitative study of metal magnetic memory signal versus local stress concentration [J]. NDT&E International, 2010, 43:513-518.

[8] Dong Lihong, Xu Binshi, Dong Shiyun, et al. Metal magnetic memory testing for early damage assessment in ferromagnetic materials [J]. Journal of Central South University of Technology, 2005, 12(S2):102-106.

[9] Ren Jilin, Lin Junming. Electromagnetic nondestructive testing [M]. Beijing: Science Press, 2008. (in Chinese)

[10] Gatelier R C, Chicois J, Fougeres R, et al. Characterization of pure iron and (130 P.P.M.) carbon-iron binary alloy by Barkhausen noise measurements: study of the influence of stress and microstructure [J]. Acta Materialia, 1998, 46(14):4873-84.

[11] Mccord J, Schafer R. Stress-induced remagnetization in magnetostrictive films [J]. Journal of Applied Physics, 2004, 95(11):6861-6863.

[12] Bulte D P, Langman R A. Origins of the magnetomechanical effect [J]. Journal of Magnetism and Magnetic Materials, 2002, 251:229-243.

[13] Lindgren M, Lepisto T. Effect of prestraining on Barkhausen noise vs. stress relation [J]. NDT&E International, 2001, 34:337-344.

[14] The qualification examination committee of ordnance industrial nondestructive testing personnel. The quick manual of magnetic properties curve of commonly used steel [M]. Beijing: China Machine Press, 2003:41.(in Chinese)

[15] Shi Changliang, Dong Shiyun, Xu Binshi, et al. Metal magnetic memory effect caused by static tension load in a case-hardened steel [J]. Journal of Magnetism and Magnetic Materials, 2010, 322(4):413-416.

(Edited by Cai Jianying)

10.15918/j.jbit1004-0579.201524.0407

TH 140/7 Document code: A Article ID: 1004- 0579(2015)04- 0471- 07

Received 2014- 03-28

Supported by the National Natural Science Foundation of China (51275048)

E-mail: zhongchaoqiu@gmail.com