Factor-graph-based iterative channel estimation and signal detection algorithm over time-varying frequency-selective fading channels

ZHAO Hong-jie(赵宏杰), WU Nan(武楠) , WANG Hua(王华),LI Zhi-xin(李智信), KUANG Jing-ming(匡镜明)

(School of Information and Electronics, Beijing Institute of Technology, Beijing 100081, China)



Factor-graph-based iterative channel estimation and signal detection algorithm over time-varying frequency-selective fading channels

ZHAO Hong-jie(赵宏杰), WU Nan(武楠), WANG Hua(王华),LI Zhi-xin(李智信), KUANG Jing-ming(匡镜明)

(School of Information and Electronics, Beijing Institute of Technology, Beijing 100081, China)

The problem of soft-input soft-output (SISO) detection for time-varying frequency-selective fading channels is considered. Based on a suitably-designed factor graph and the sum-product algorithm, a low-complexity iterative message passing scheme is proposed for joint channel estimation, equalization and decoding. Two kinds of schedules (parallel and serial) are adopted in message updates to produce two algorithms with different latency. The computational complexity per iteration of the proposed algorithms grows only linearly with the channel length, which is a significantly decrease compared to the optimal maximum a posteriori (MAP) detection with the exponential complexity. Computer simulations demonstrate the effectiveness of the proposed schemes in terms of bit error rate performance.

factor graph; message passing; frequency-selective fading channel; soft-input soft-output (SISO) detection; turbo equalization

In wireless communication systems, inter-symbol interference (ISI) results in unacceptable detection over frequency-selective fading channels. Thus the equalization strategies are necessary to compensate the ISI efficiently. The optimal equalizer can be implemented by the max a posteriori (MAP) algorithm, or the Viterbi and soft-output Viterbi algorithms[1]. However, these optimal equalizers suffer high complexity and depend on acquisition of the exact channel state information. Therefore, joint channel estimation and equalization algorithm is demanded for practical applications.

In the last decade, turbo equalization[2]has been proven to be a near-optimal solution with reasonable complexity[3-4]. Recently, the iterative receivers have been redesigned by factor graphs and message passing algorithms for their low complexity[5-8]. Several new algorithms were developed for both unconstrained and constrained linear equalization[9]. Focusing on channels with known ISI, FDM and CDMA systems, some novel algorithms for SISO detection were presented over linear channels with reduced complexity[10]. Some other problems have also been benefited from message passing algorithms, for instance, SISO detection in MIMO systems[11-13], iterative multiuser detection in CDMA systems[14-15], and iterative receiver in strong phase noise channels[16-17], etc.

In consideration of rapidly time variations of wireless channels due to high mobility and unavailability of CSI at the receiver, this paper proposes an iterative soft-in soft-output detection scheme by applying message passing algorithm on a suitable designed factor graph for joint channel estimation, equalization and decoding over frequency-selective fading channels. The computational complexity of the proposed detector increases only linearly with the channel memory length, which is a significant reduction compared with the optimal MAP detection.

1 System model

Consider an LDPC-coded singer-carrier communication system over a frequency-selective Rayleigh fading channel of lengthL. At the transmitter, information bit sequenceb{bk} is first encoded to produce the coded bit sequencec{ck}, denoted by encoding functionc=fc(b)∈C. The coded bits are mapped to symbol sequencex{xk} byM-PSK constellation A, denoted by mapping functionx=fx(c)∈A, and then transmitted over frequency-selective Rayleigh fading channel. At the receiver, assuming perfect carrier recovery and timing synchronization, the equivalent baseband received signal at time instantkis given by

(1)

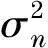
(2)

r=Hx+n

(3)

where H is a (K+L-1)×KToeplitz channel matrix with entries

(4)

Throughout this paper,knowledge of the channel matrix H and the statistics of the noise vectornare practically unknown and have to be estimated at receiver side.

2 Factor graph representation

The optimal decision rule that minimizes bit error rate (BER) follows the maximum a posteriori (MAP) criterion[1], given by

(5)

whereP(bi|r) denotes the a posteriori probability mass function (pmf) of theith information bitbigiven the received signal vector r. This can be obtained by marginalizing the joint posterior probability distribution functionp(b,c,x,H|r), which can be factorized as

p(b,c,x,H|r)∝p(r|x,H)p(x|c)p(c|b)p(b)p(H)∝I[c=fc(b)]I[x=fx(c)]p(r|x,H)p(b)p(H)

(6)

whereI[c=fc(b)] andI[x=fx(c)] denote the code and mapping constraint indicator function, respectively.p(b) defines the a priori bit information which can be factorized easily according to the uniform i.i.d. assumption.

The factorization ofp(b,c,x,H|r) leads to the factor graph representation shown in Fig.1, where the factor nodesp(r|x,H) andp(H) correspond to the equalizer and channel estimator, respectively. Applying sum-product algorithm (SPA) on the FG, we can obtain a suboptimal but low complexity iterative message passing algorithm since the graph is cyclic[6]. The equalizer uses the received signal vector, the channel state information and the a priori information from the decoder to compute extrinsic log-likelihoods of every transmitted symbol, which are then soft demapped and decoded. The SISO decoder compute extrinsic log-likelihood ratios (LLRs), which will be fed into the equalizer and channel estimator as a priori information after soft mapping. After several iterations of soft information exchange between the SISO decoder, SISO equalizer and the channel estimator, it is stopped when a maximum iteration number is reached. Then the estimates of transmitted information bits can be obtained by the channel decoder with hard decision.

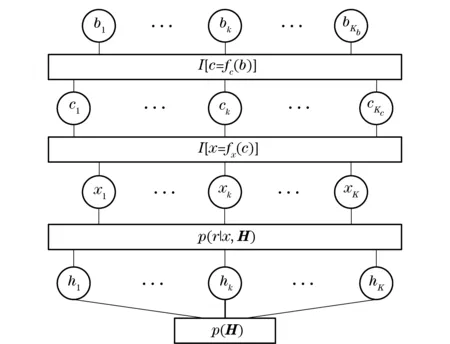
Fig.1 Factor graph of the factorization in Eq.(6)

3 Proposed message passing algorithm

3.1 Decoder and demapper

(7)

(8)

(9)

3.2 Channel estimator

Since the channel taps are continuous random variables, the messages propagating on edges adjacent to the channel tap nodes are probability density functions (pdfs). The SPA applied for continuous random variables involves the integration of pdfs, which lead to intractable computations for practical implementation. Thus, we use parameterized canonical distributions[6]as the outgoing messages of the channel tap nodes. Specifically, the impulse at estimated value is selected to approximate the actual density of the channel tap, given by

pu(hk)=δ(hk-k)

(10)

which further simplifies the message calculation of the equalizer nodes in next section. Then only the estimated valuekat time indexkneeds to be computed. The optimal linear minimum mean square error (LMMSE) estimate[16]of the complex channel tap can be obtained by

(11)

whereNis the length (assumed odd) of a finite-impulse response (FIR) filter and the filter coefficientsωi,jcan be obtained by solving the Wiener-Hopf equations[3]. Note that the optimal Wiener solution requires knowledge of the channel autocorrelation function and the matrix inverse calculation. If the normalized fade rate is slow (fdTs≪1) and the filter lengthNis small enough (N≪(fdTs)-1), we can approximate the filter coefficients to be equal as

(12)

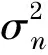
(13)

At first iteration, only pilot symbols are used to calculate the initial estimates of the channel taps and noise variance. In subsequent iterations, symbol estimates and pilot symbols are used together to obtain refined channel estimates.

3.3 SISO detector

The likelihood functionp(r|x,H) can be expressed as

(14)

(15)

with the functions

(16)

(17)

Fig.2 shows the detector section for three time instants of the corresponding factor graph in Fig. 1. The nodeUk,ldenotes the inter-symbol interference betweenxkandxk-l. Note that the marginalization cannot be exactly carried out by applying the SPA to the factor graph in Fig.2 as it contains cycles[6]. On the other hand, we can see that the cycles cannot be lower than six according to the factorization in Eq.(15). Therefore, in this case SPA can make a good approximation of the exact marginalization.

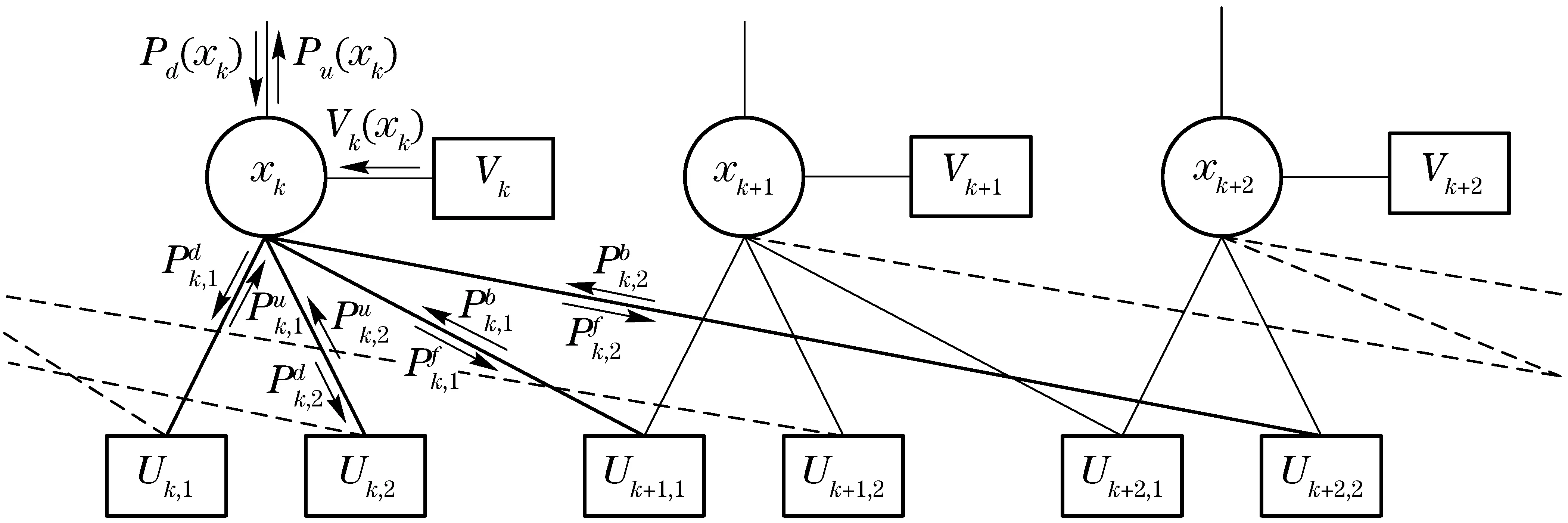
Fig.2 Three equalizer sections of the factor graph for L=3

(18)

(19)

(20)

(21)

(22)

(23)

Based on the factorization method in Eq.(15), we note that function nodesUk,lalways have degree of two, whose number increases linearly with the length of the channel. Thus, the describing message passing algorithm has a complexity per iteration which is linear with the channel length. It is a significant complexity reduction compared to the optimal MAP symbol detection with exponential complexity in the number of channel length.

3.4 Schedule

Due to the existence of cycles in the FG, the schedule for the message passing cannot be unique[6]. Here, we employ two different schedules, which result in two different SISO equalizers. One is a parallel schedule inspired by flooding schedule in LDPC decoding whose latency does not depend on the symbol lengthK. The other is a serial schedule executed by the forward and backward recursion with latency linearly increasing with the symbol lengthK. Both schedules iterate only once before passing out the extrinsic messages due to more self-iterations can provide negligible gains[10]. For parallel schedule, the message computation sequence is as follows.

① Update allPAPP(xk) in parallel for allk.

④ Update allPAPP(xk) again and then calculate all extrinsic messagesPu(xk) for allk.

For serial schedule, the message computation sequence is as follows.

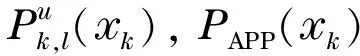
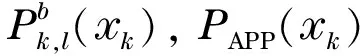
③ Update all messagesPu(xk).

Finally, the message updating schedule for the entire factor graph starts from the initialization of channel estimation based on pilot symbols. Then a parallel or serial schedule is executed just one self-iteration before sending the extrinsic messages to the decoder. The decoder uses standard belief propagation decoding algorithm to calculate the a posteriori probability of information bits and feeds back extrinsic information to the detector and channel estimator. The algorithm stops if a valid codeword is found by checking the code syndrome or a predefined iteration number is reached.

4 Simulation results

Computer simulations are conducted to evaluate the performance of the proposed algorithms for single-carrier coded transmission system. The BER performances of several schemes are compared. The first is pilot-based channel estimation using linear interpolation with no iteration. The second is a genie-aided receiver using the proposed detector with perfect knowledge of the channel. The third uses the proposed message passing algorithm for iterative channel estimation and detection with serial/parallel schedules. Moreover, the optimal performance bound, denoted by AWGN bound which corresponds to the system under AWGN channel without ISI, is also shown as a reference benchmark. The simulation uses a (3,6)-regular LDPC code with codeword length of 1920 and gray-mapping QPSK modulation. The channel length isL=3 with equal average power and the total energy are normalized to unity. A typical Doppler ratefDTs=0.005 is considered and each pilot symbol is periodically inserted in every 20 data symbols for the initialization of channel estimation. The length of moving average filter is selected asN=75. A maximum of 10 iterations is allowed. The results are averaged over Monte Carlo simulations after 1 000 independent bit errors are observed.

Fig. 3 shows the BER performance of the proposed algorithm compared with other receiver schemes. As no feedback information from decoder is used to assist channel estimation and equalization, the pilot-based non-iterative receiving algorithm has a poor BER performance, when BER=10-4there is about 7.9 dB SNR loss compared to the optimal MAP detector. On the other hand, when the CSI is known at receiver, factor-graph-based joint iterative equalization and decoding algorithms can continually increase the estimation accuracy of symbol posterior probability at the equalizer by iteratively exchanging soft information of the symbols between equalizer node and decoder node in factor graph, and then significantly improve the BER performance of the decoder. As we can seen in Fig.3, the above-mentioned algorithms can achieve the BER performance close to the optimal MAP detection, in which the algorithms based on serial schedule and parallel schedule exist only 0.45 dB and 0.70 dB SNR loss respectively. However, due to low latency characteristics, the parallel schedule is more applicable in practical implementation. Moreover, the computational complexity of the iterative message passing algorithm can achieve only linearly to the channel memory length, which is a great reduction compared to the optimal MAP symbol detector with exponential complexity. When the CSI is unknown at receiver, the proposed iterative message passing algorithms for joint channel estimation, equalization and decoding could also obtain favorable performance with low complexity. Compared with the known CSI case, the algorithms based on serial schedule and parallel schedule exist 1.95 dB and 1.80 dB SNR loss respectively.

Fig.3 BER performance of the proposed algorithm

Fig. 4 shows the performance of channel estimation in terms of mean square error (MSE) versus SNR. The MMSE of the optimal Wiener filter is also given as a reference lower bound. As can be seen, the MSE of channel estimation decreases with the increase of SNR and the number of iteration. Only after first iteration, the MSE of the proposed algorithm is significantly lower than that of pilot-based algorithm. After 10 iterations of message passing, the MSE of the proposed algorithm gradually approaches the MMSE bound within high SNR region, as high reliability of symbol extrinsic information can be obtained from decoder feedback.

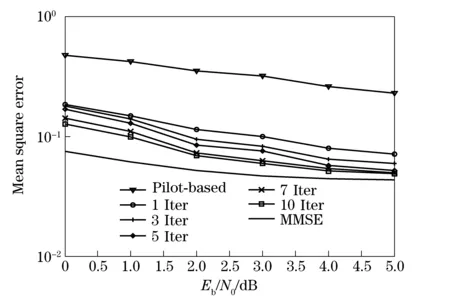
Fig.4 MSE performance of channel estimation

5 Conclusion

In this paper, we have proposed a SISO detector for iteratively joint channel estimation, equalization and decoding over frequency-selective fading channel. The proposed detector is obtained by applying SPA to a suitable designed factor graph, which represents the factorization of the joint posterior probability distribution function of the transmitted symbols and the channel coefficients. Based on SPA, we derive the message computation rules and develop two different schedules for message updates. Simulation results show that, the proposed algorithms with both schedules can achieve a satisfactory BER performance after several iterations, while with a significant complexity reduction with respect to the optimal MAP detector.

[1] Tse D, Viswanath P. Fundamentals of wireless communications [M]. Cambridge: Cambridge University Press, 2005.

[2] Koetter R, Singer A C, Tuchler M. Turbo equalization [J]. IEEE Signal Processing Magazine, 2004, 21(1):67-80.

[3] Valenti M C, Woerner B D. Iterative channel estimation and decoding of pilot symbol assisted turbo codes over flat-fading channels [J]. IEEE Journal on Selected Areas in Communications, 2001, 19(9): 1697-1705.

[4] Su H J, Geraniotis E. Low-complexity joint channel estimation and decoding for pilot symbol-assisted modulation and multiple differential detection systems with correlated Rayleigh fading [J]. IEEE Transactions on Communication, 2002, 50(2): 249-261.

[5] Wymeersch H. Iterative receiver design [M]. Cambridge: Cambridge University Press, 2007.

[6] Kschischang F R, Frey B J, Loeliger H A. Factor graphs and the sum-product algorithm [J]. IEEE Transactions on Information Theory, 2001, 47(2): 498-519.

[7] Colavolpe G, Germi G. Simple iterative detection schemes for ISI channels [C]∥International Symposium on Turbo Codes & Related Topics, Brest, France, 2003.

[8] Lu B, Yue G S, Wang X D, et al. Factor-graph-based soft self-iterative equalizer for multipath channels [J]. EURASIP Journal on Wireless Communications and Networking, 2005, 2005(2): 187-196.

[9] Drost R J, Singer A C. Factor-graph algorithms for equalization [J]. IEEE Transactions on Signal Processing, 2007, 55(5): 2052-2065.

[10] Colavolpe G, Fertonani D, Piemontese A. SISO detection over linear channels with linear complexity in the number of interferers [J]. IEEE Journal of Selected Topics in Signal Processing, 2011, 5(8): 1475-1485.

[11] Etzlinger B, Haselmayr W, Springer A. Equalization algorithms for MIMO communication systems based on factor graphs [C]∥2011 IEEE International Conference on Communication, Kyoto, Japan, 2011.

[12] Kaynak M N, Duman T M, Kurtas E M. Belief propagation over SISO/MIMO frequency selective channels [J]. IEEE Transaction on Wireless Communications, 2007, 6(6): 2001-2005.

[13] Haselmayr W, Etzlinger B, Springer A. Factor-graph-based soft-input soft-output detection for frequency-selective MIMO channels [J]. IEEE Communication Letter, 2012, 16(10): 1624-1627.

[14] Tan P H, Rasmussen L K. Belief propagation for coded multiuser detection [C]∥IEEE International Symposium on Information Theory, Seattle, the United States, 2006.

[15] Aktas E. Iterative message passing for pilot-assisted multiuser detection in MC-CDMA systems [J]. IEEE Transaction on Communications, 2012, 60(11): 3353-3364.

[16] Zhao H J, Wu N, Wang H, et al. Factor-graph-based iterative receiver design in the presence of strong phase noise[C]∥IEEE Vehicular Technology Conference Spring, Yokohama, Japan, 2012.

[17] Zhao H J, Wu N, Wang H, et al. Particle swarm enhanced graph-based iterative receiver with phase noise and frequency offset [C]∥Wireless Communications and Signal Processing, Hangzhou, China, 2013.

[18] Haykin S. Adaptive filter theory information and system science series[M]. Englewood Cliffs, NJ: Prentice-Hall, 1996.

(Edited by Cai Jianying)

10.15918/j.jbit1004-0579.201524.0410

TN 911 Document code: A Article ID: 1004- 0579(2015)04- 0494- 07

Received 2014- 03- 28

Supported by the National Natural Science Foundation of China(61201181)；Specialized Research Fund for the Doctoral Program of Higher Education(20121101120020);the Co-innovation Laboratory of Aerospace Broadband Network Technology

E-mail: wunan@bit.edu.cn