三维球体的贝特朗奇论问题

石业娇, 孟宪涛

(1.大连海洋大学 应用技术学院, 辽宁 大连 116300; 2.沈阳师范大学 数学与系统科学学院, 沈阳 110034)



三维球体的贝特朗奇论问题

石业娇1, 孟宪涛2

(1.大连海洋大学 应用技术学院, 辽宁 大连 116300; 2.沈阳师范大学 数学与系统科学学院, 沈阳 110034)

介绍了平面上圆的随机弦的贝特朗奇论问题,指出了奇论问题具有无穷多个答案,并且答案在一个区间内可连续取值,给出了奇论问题的简单解析,把圆上奇论问题推广到三维空间情形,得出三维球体的贝特朗奇论问题。根据不同的球截面构造方法,给出奇论问题的8种不同解法,得到三维球体贝特朗奇论问题具有无穷多个答案的结论,且除去个别答案之外,其余答案可在一个区间上连续取值。对各种解法进行解析,发现与圆上奇论问题类似,各种解法所确立的随机试验各异是造成一题多种答案的直接原因,而根本原因则是在构造随机弦时对任意性理解的差异。

随机截面; 随机试验; 几何概率; 奇论

0 引 言

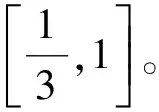
1 球截面的奇论问题

在半径为R的球上任意作一截面,截面的面积大于球内接正四面体一个侧面所在球截面面积的概率P。

图1 三维空间中球的随机截面概率的奇论问题

先求出球内接正四面体一个侧面所在的球截面面积和球心到内接正四面体侧面的距离。设半径为R的球内接正四面体V-ABC,如图1,其一边长设为a,则有

2 具体解法

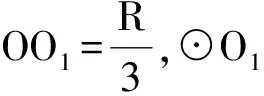
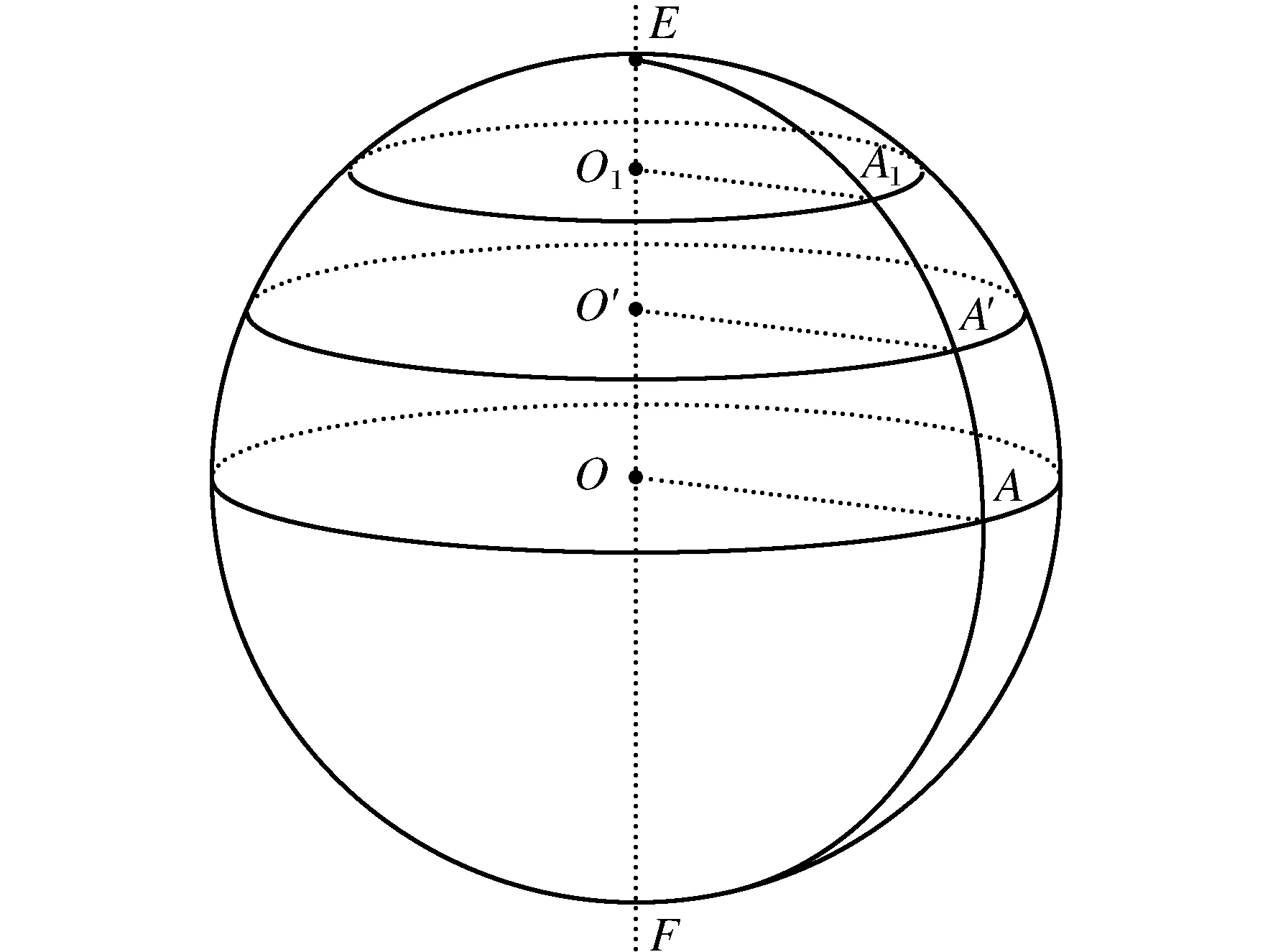
图2 解法1～解法3构造方法

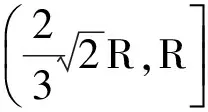
图3 解法4～解法8构造方法

解法6 取球面上一定点A,过A点任作球O的切线MN,再过直线MN作任一平面α,则α与球相交于球的截面⊙O′。设⊙O′中过A点的直径的另一顶点为D,则易知过A,D两点球的大圆与⊙O′垂直,且当过直线MN的平面α变化时,D点就在该大圆上移动。取D点为随机点,根据截面的任意性,可认为D点在过A点且与平面α垂直的大圆上是均匀分布的。

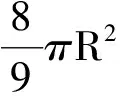
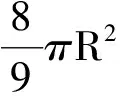
解法8 设MN为球O的一条定弦,记MN=2AM=2d。过弦MN作球O任意截面⊙O′。

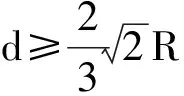
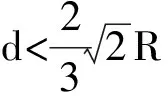
分析此概率P的表达式可知,P是d的连续函数,而且是d的增函数。当d=0时(此时弦MN退化为球面上一点),求得

3 结 语

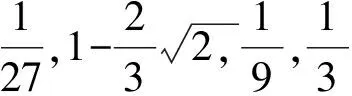
以上得到的各种问题答案是相对于不同的随机试验得到的,而每一种随机试验又是相对于一种随机截面的构造方法确定的,每一种随机截面的构造方法又是基于对随机截面任意性的不同理解所形成的。因此可以说,每一种答案都是正确的。所以这都是由原问题提出的不确定原因,造成了人们在理解上的差异所致。

[1]盛骤,谢式千,潘承毅.概率论与数理统计[M].4版.北京:高等教育出版社, 2008.

[2]茆诗松,程依明,濮晓龙.概率论与数理统计教程[M].北京:高等教育出版社, 2004.

[3]郭存娣.谈二维随机变量的函数的分布函数[J].高等数学研究, 2003,3(3):37-39.

[4]吕洪升,张千祥.二维连续型随机变量相关计算的积分限确定问题[J].大学数学, 2011,27(3) :194-100.

[5]王翠茹,田振清.两随机变量简单相关系数图式的算法设计[J].中国教育技术装备, 2011(6):69-70.

[6]欧阳敏华.二元随机变量相依关系的图示判别[J].统计与决策, 2012(3):27-29.

[7]王志祥.不同类型随机变量和差积商的分布[J].高等数学研究, 2010,13(4):97-99.

[8]彭刚,禹辉煌.二维离散型随机变量独立性判别定理及应用[J].湖南理工学院学报:自然科学版, 2010,23(2):23-25.

[9]任咏红,张晓有,马燕妮.概率约束规划问题的一个光滑近似[J].辽宁师范大学学报:自然科学版, 2013,36(1):7-10.

[10]崔书英.两个连续型随机变量相互独立判定定理[J].中国煤炭经济学院学报, 1996(4):85-87.

[11]李德新,陈聪.随机变量独立性的直接判别法[J].高等数学研究, 2008,11(4):54-57.

[12]冬喜.两组变量间相关关系的统计分析方法[J].高等数学研究, 2011,14(1):75-76.

[13]刘杨,李雪丹.几何概型中“殊途各异”问题的研究[J].中国数学教育, 2012(3):21-23.

Three-dimensional sphere Bertrand paradox problem

SHIYejiao1,MENGXiantao2

(1.Applied Technology College, Dalian Ocean University, Dalian 116300, China;2.School of Mathematics and Systems Science, Shenyang Normal University, Shenyang 110034, China)

This paper introduces the Bertrand paradox problem in a random string on the circle, pointing out that this paradox has infinite answers of continuous values in an intervals and gives a simple analysis to the paradox.The paradox of circle can be applied into the three-dimensional space to obtain the conclusion of Bertrand paradox in three-dimensional sphere.According to the different ball section, eight different solutions to this problem are presented in this paper, proving that three-dimensional sphere Bertrand paradox has infinite answers.Despite individual answer, the rest of the answers can be obtained in a continuous interval.Through analyzing all solutions, we can find similar situations with paradox problem.The immediate reason causing a number of answers is the different randomized trial results, while the essential reason is different understanding of the arbitrary concept when constructing the random string.

random section; random test; geometric probability; paradox problem

2014-02-27。

辽宁省教育厅高等学校科学研究项目(20060842); 辽宁省高等教育教学改革研究项目(辽教发[2009]141号)。

石业娇(1970-),女,辽宁瓦房店人,大连海洋大学副教授,硕士。

1673-5862(2015)01-0064-04

O211

A

10.3969/ j.issn.1673-5862.2015.01.014