基于模糊PID控制算法的导盲机器人研究

2015-04-21张志美程立英赵以恒吴海元

沈阳师范大学学报(自然科学版) 2015年1期

关键词：导盲循迹变化率

张志美, 程立英, 赵以恒, 吴海元

(沈阳师范大学物理科学与技术学院, 沈阳 110034)

基于模糊PID控制算法的导盲机器人研究

张志美, 程立英, 赵以恒, 吴海元

(沈阳师范大学物理科学与技术学院, 沈阳 110034)

结合PID控制对线性定常系统控制的优越性和模糊控制器对复杂非线性系统的有效控制,设计了一种基于模糊PID控制算法实现导盲机器人的避障循迹控制。导盲机器人采用乐高套件搭建而成,避障环节设计采用超声波传感器检测障碍物信息,控制器采集障碍物信息及机器人行驶速度信息,利用模糊PID算法实现避障;循迹环节为克服遇机器人转弯或高速行进时一般PID控制算法稳定性差的不足,采用实时跟踪偏差和偏差变化率来修正PID控制的各个参数,实现对机器人的导航控制,其中机构采用红外传感器进行识别检测。实验结果表明,利用改进算法进行导盲机器人的避障循迹控制,能够极大的提高避障的准确率,精准的循迹。

模糊PID算法; 导盲机器人; 循迹避障

0 引言

随着社会生产技术的不断发展,机器人的应用领域也在不断扩展。机器人正跳脱以往在生产中负责生产、制造、搬运等任务的范畴,从传统的工业型走向服务型。导盲机器人[1]是服务型机器人,专为盲人设计,主要功能实现循迹、避障与交通路口的红绿灯辨别。机器人避障问题是当今机器人研究领域的一个焦点问题,在避开障碍物的过程中,机器人经常面临无法预测环境变化的问题,这是由于机器人从传感器[2]所得到的信号是不连续的、不安全的、不可靠的,所以这就造成了机器人避障成为当今机器人研究领域的焦点[3]。国内在研究机器人的避障及路径规划方面起步较晚,现阶段的大多数研究也都处于单项研究阶段。目前常用的控制算法是将遗传算法、模糊控制以及神经网络等人工智能方法等应用到PID控制算法中[4-6],以提高避障精度、加快规划速度从而满足实际应用需求。

由于本设计是基于导盲机器人的避障循迹控制研究,系统要求所设计的控制算法具有实时性好、处理速度快、辨识精度高。由于智能算法如BP神经网络、遗传算法的实时性差,本设计采用模糊控制算法与PID算法的结合,即模糊PID算法[7-8],并改进模糊控制参数,使得系统具有良好的实时性,且处理速度快,由于其处理的高效性提高了系统对避障参数的处理和分析能力,进一步提升了系统避障的能力。

1 改进的模糊PID算法

模糊控制是智能控制的一种典型的重要分支,它不依赖于被控对象的数学模型,主要依靠现场操作人员或相关专家的判断、经验或历史数据等先验知识,实现对系统的实时控制。

基本PID算法因其依赖被控对象精确的数学模型,对非线性、时变的复杂控制系统及控制环境复杂的系统难以获得满意的效果。模糊PID算法是结合模糊控制与PID算法,通过建立相应的模糊控制表,根据系统偏差、偏差变化率查表得到比例、积分和微分的系数3个参数的整定值,实现PID运算。控制的关键是根据实时环境、专家经验等因素建立模糊控制表。图1所示模糊PID控制系统框图。

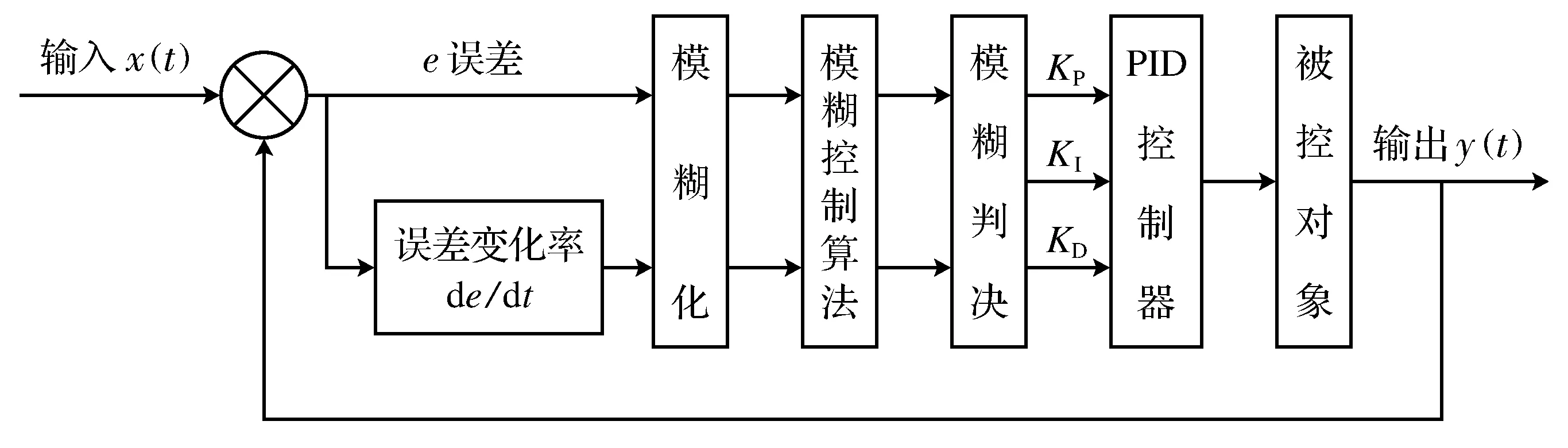
图1 模糊PID控制系统框图

模糊PID控制系统[8-11]以被控对象的反馈值与目标值的误差e(t)和误差变化率de(t)/dt作为系统输入,采用模糊算法对PID参数进行实时调整,以满足实际控制环境对被控对象的要求,具有良好的适应能力。

2 导盲机器人循迹算法设计

导盲机器人循迹过程中在转弯或高速运动的情况下,常规PID算法的稳定性差[12-14]。本设计采用实时跟踪偏差和偏差变化率来修正PID控制的各个参数,即模糊PID控制算法实现对机器人的控制。

PID算法表示如下:

其中:KP为比例系数;KI为积分系数;KD为微分系数。模糊自整定PID参数的目的是使参数KP、KI、KD随着误差e(t)和误差变化率de(t)/dt的变化而自行调整。

根据导盲机器人的控制要求,将系统误差e(t)和误差变化率de(t)/dt作为模糊控制的输入语言变量,KP、KI、KD作为输出语言变量。为提高控制器主动适应系统或环境的能力,控制器参数KP、KI、KD的初值由用户根据环境因素及经验输入,提高用户对控制参数的宏调节能力,弥补模糊推理中对变量进行模糊化所造成的误差。其中5个语言变量的量化等级定为7级,即e(t)、de(t)/dt、KP、KI、KD={-3,-2,-1,0,1,2,3},模糊子集为{NB,NM,NS,O,PS,PM,PB},对应值代表负大,负中,负小,零,正小,正中,正大。模糊集上的基本论域变化范围为{-3,3},将基本论域范围连续变化的量分级离散化,量化方式采用非线性量化,然后进行模糊处理。本系统采用三角形隶属度函数,以简化模糊推理的计算过程。表1所示输入输出变量的隶属度函数表。

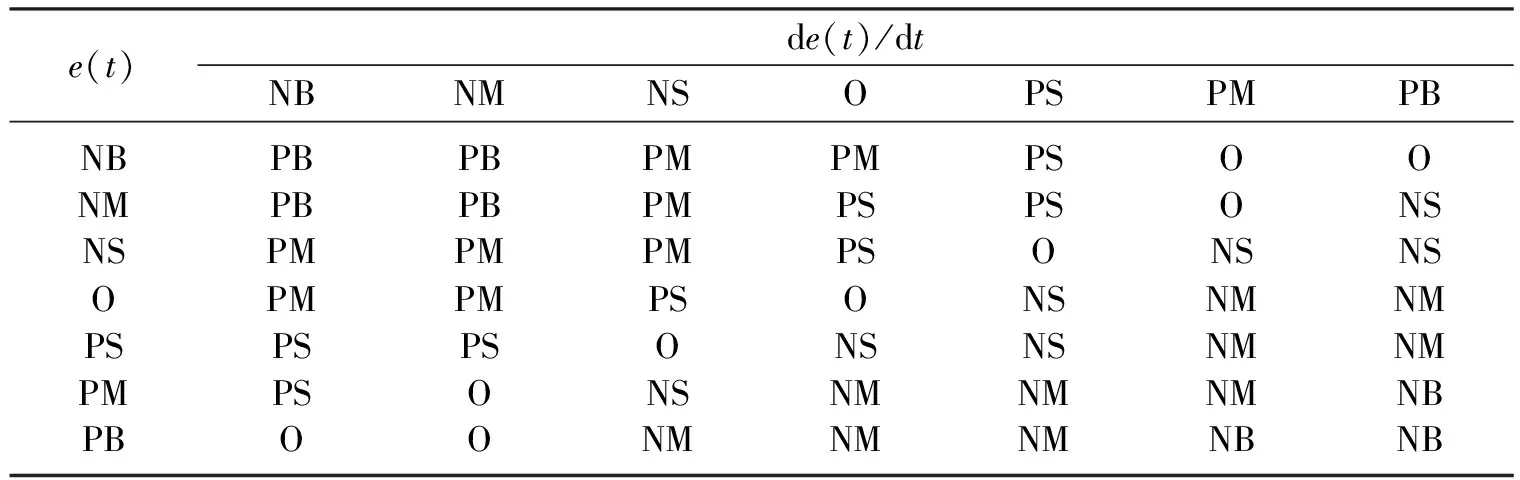
表1 误差e(t),误差变化率de(t)/dt,KP,KD,KI隶属度表

根据导盲机器人控制经验采用如下规则:

1) 当轨迹误差e(t)较大时,为了加快循迹的响应速度,取较大的KP;同时为了避免由于运行中对于直角转弯区误差e(t)瞬时变大可能出现的微分饱和而使控制作用超出许可的范围,导致超调的发生,应取较小的KP;若系统响应出现较大的超调,产生积分饱和,此时令KP=0去掉积分作用。

2) 当误差|e(t)|和误差变化率|de(t)/dt|大小适中时,KP应取得小些,确保系统响应具有较小的超调。KD和KI应取值适合,此时KD对系统响应的影响较大。

4) 误差变化率|de(t)/dt|表明导盲机器人循迹误差变化的快慢速度,|de(t)/dt|越大,KP取值越小,KI取值越大。

系统建立ΔKP,ΔKI,ΔKD的控制规则表如表2所示。

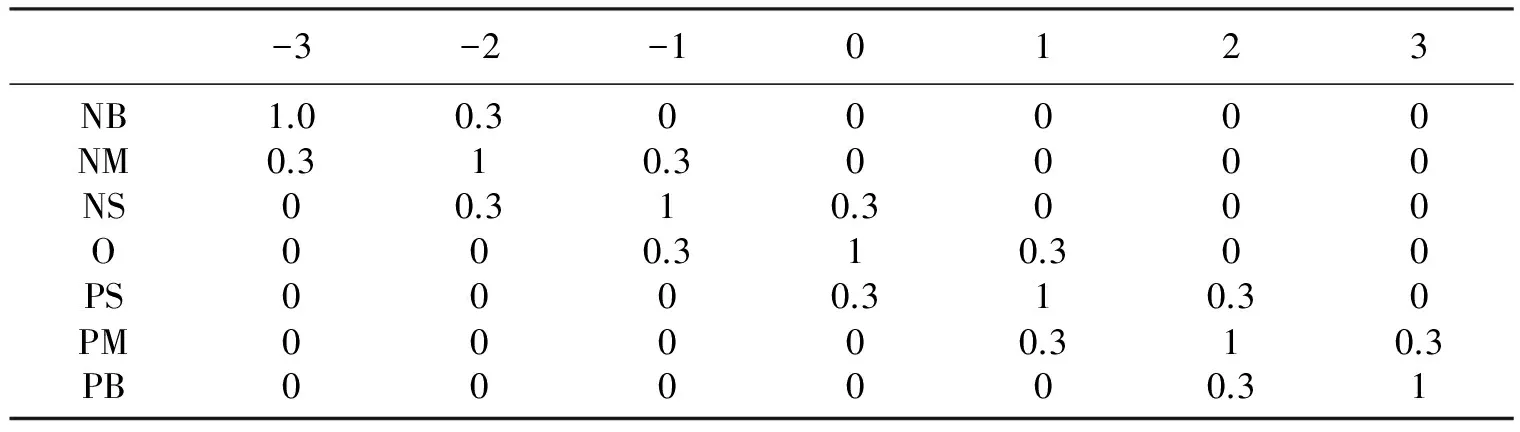
表2 模糊变量ΔKP的模糊规则表

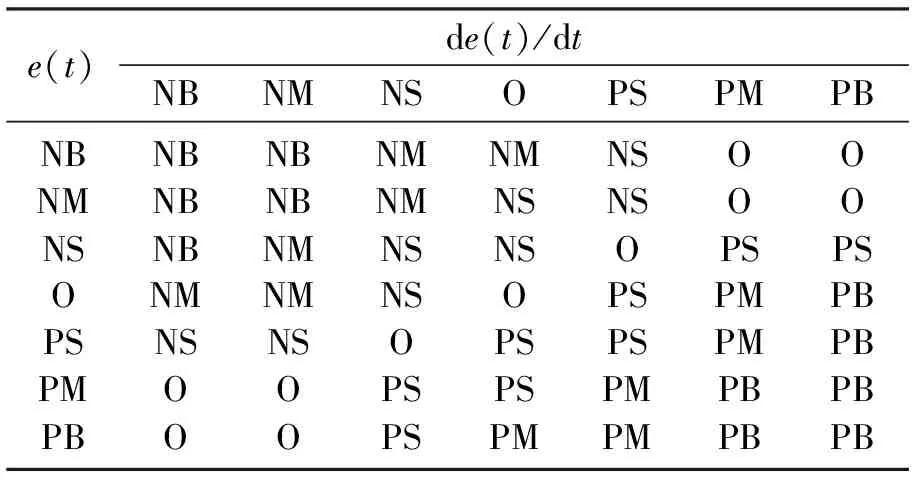
表3 模糊变量ΔKI的模糊规则表

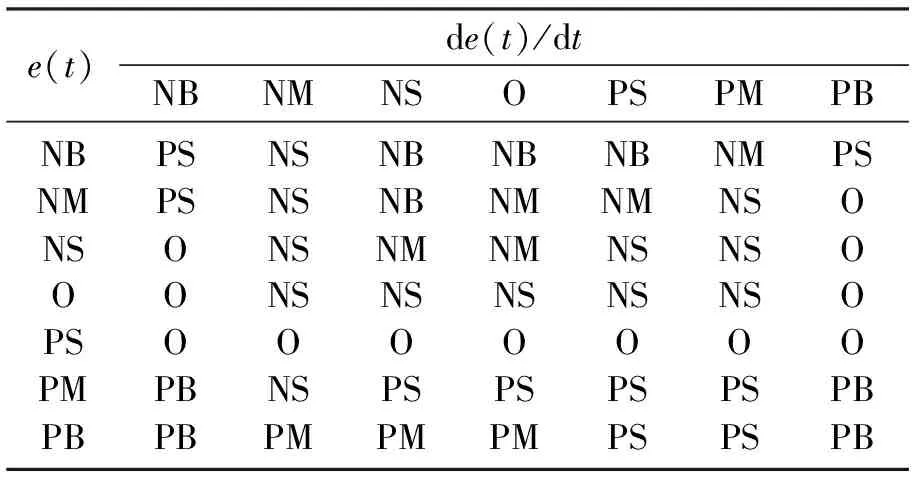
表4 模糊变量ΔKD的模糊规则表

通过查询模糊控制表得到PID参数的修正量ΔKP,ΔKI和ΔKD,其相应的参数计算如下:

KP=KP0+ΔKP

KI=KI0+ΔKI

KD=KD0+ΔKD

式中:KP0,KI0,KD0是PID控制器的初值,一般根据现场调试经验设定。

3 仿真实验与硬件实现

3.1 基于模糊PID控制算法的仿真实现导盲机器人的避障循迹控制

系统采用传统的PID控制,仿真结构图如图2所示。

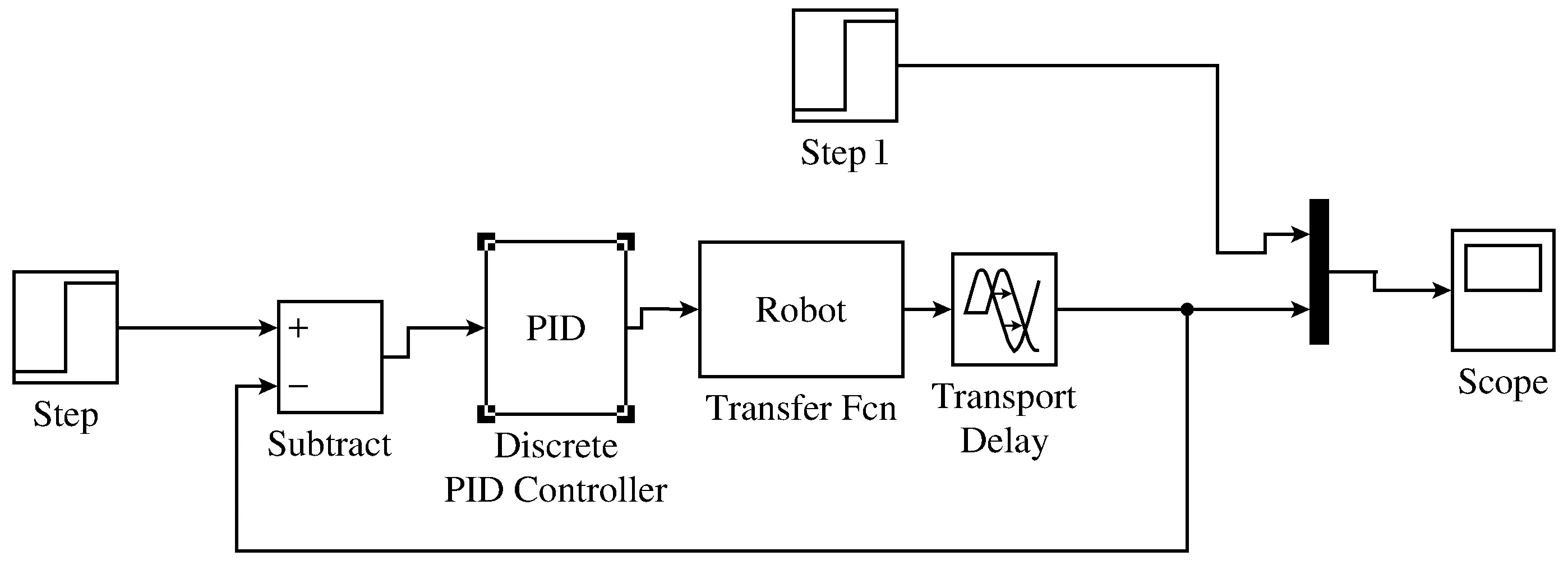
图2 PID控制系统仿真结构图

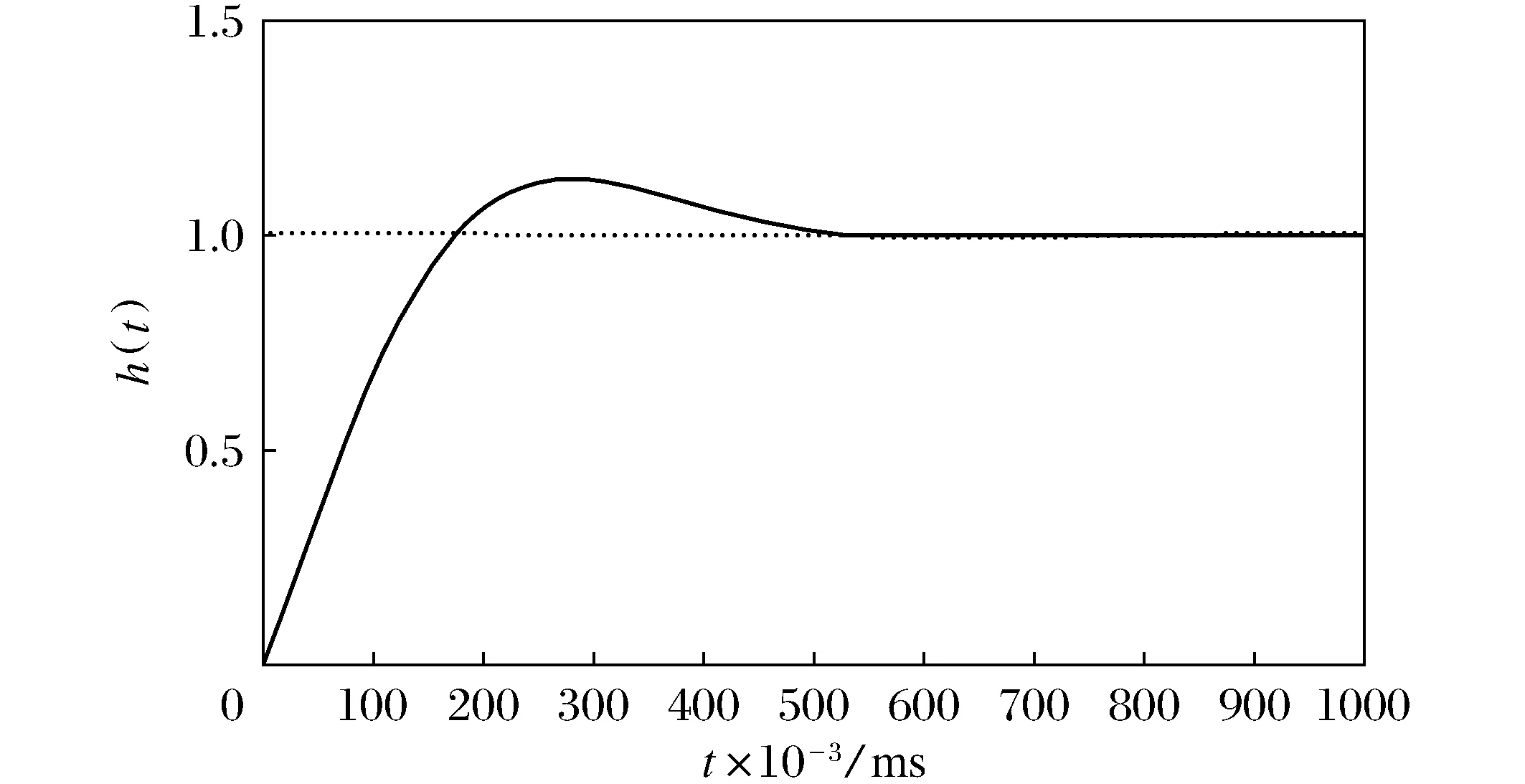
图3 PID控制响应曲线

在图中的PID模块中对3个参数进行设定,通过不断调整PID三参数,得到最佳仿真曲线,其中,KP=2,KI=0.018,KD=0.01,仿真结果如图3所示。

图3反映导盲机器人循迹的响应曲线,横轴为响应时间t,单位为ms,纵轴为阶跃响应h(t)。由图可知调节时间为0.4 ms,超调量约20%左右,稳态误差为0。

采用模糊PID控制,系统仿真结构如图4所示。

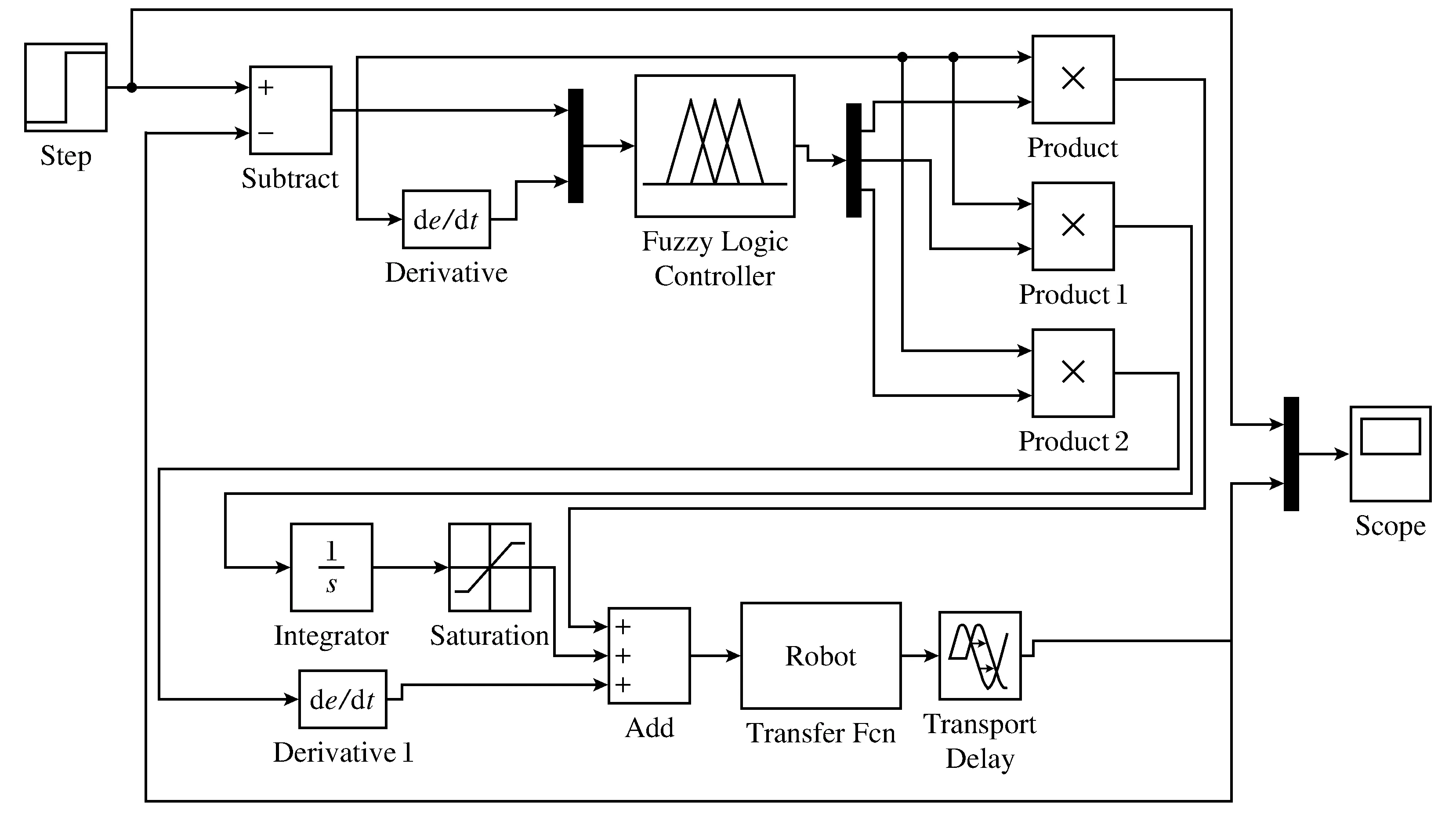
图4 模糊PID控制系统仿真结构

仿真结果如图5所示,调节时间为0.18 ms,超调量为0,稳态误差为0。

3.2 导盲机器人硬件系统调试

系统采用乐高机器人套件[15-16]组合,硬件结构如图6所示。

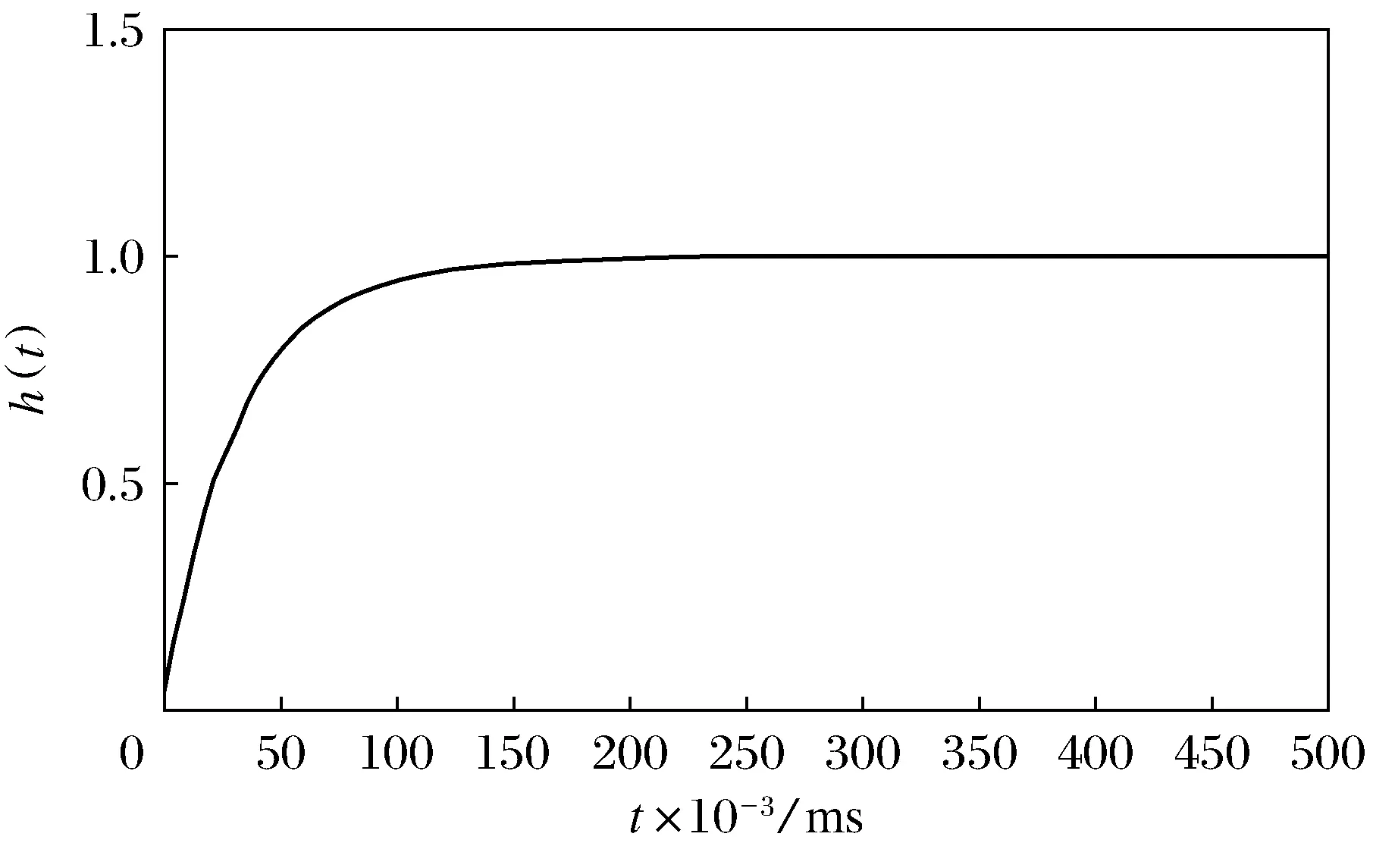
图5 模糊PID控制响应曲线

图6 导盲机器人硬件结构图

系统在乐高NXT软件环境下编程控制,控制结构如图7所示。

图7 导盲机器人循迹避障结构图

图8 循迹现场测试图

实验采用上述模糊PID调节控制机器人的循迹,循迹如图8所示。根据现场测试机器人在转弯和急速运行中的稳定性好,较好地实现精确循迹,快速反应,绕过障碍物后能快速回到循迹路线上。

通过对导盲机器人的调试,测试轨迹在黑色硬纸条的轨道上进行的,用纸箱作为障碍物,循迹避障测试5次,轨道长度约2 m,结果如表5所示。

表5 测试结果

4 结语

从测试结果可以看出,采用模糊PID控制算法,小车的循迹与避障速度大大提高。小车能很好的完成循迹功能,对于s道和直角道,轨迹小车能良好地完成循迹功能。由于算法不具备自学习的能力,对于随机障碍物的避障能力还有待提高。今后将进一步改进系统结构与算法的自学习能力,提高导盲机器人的循迹避障能力,为盲人提供切实有效的帮助。

[1]黄大志,申屠留芳,郭燕.导盲机器人中超声波测距系统的研究[J].淮海工学院学报:自然科学版, 2009,18(1):19-22.

[2]王俊峰,孟令启.超声波传感器应用技术[M].北京:机械工业出版社, 2006.

[3]常健,吴成东,李斌.移动机器人避障方法综述[J].仪器仪表学报, 2010,31(8):439-442.

[4]徐兆棣,李晓毅.线性时滞系统时滞相关稳定性分析研究进展[J].沈阳师范大学学报:自然科学版, 2013,31(2):162-168.

[5]王达开.基于backstepping的自适应模糊控制及应用[J].沈阳师范大学学报:自然科学版, 2013,31(2):192-195.

[6]田琦,李琪,姚鹏,等.基于模糊PID的全方位移动机器人运动控制[J].电子科技, 2011,24(9):131-133,139.

[7]王述彦,师宇,冯忠绪.基于模糊PID控制器的控制方法研究[J].机械科学与技术, 2011,30(1):166-172.

[8]张泾周,杨伟静,张安祥.模糊自适应PID控制的研究及应用仿真[J].计算机仿真, 2009,26(9):132-135.

[9]陆华才,徐月同,刘鹏鹏,等.永磁直线同步电机进给系统模糊PID控制[J].电工技术学报, 2007,22(4):59-63.

[10]樊开阳,林小兰.基于Matlab GUI的直流电机PID调速系统的设计[J].微型机与应用, 2013,32(22):62-65.

[11]王葳,张永科,刘鹏鹏,等.无刷直流电机模糊PID控制系统研究与仿真[J].计算机仿真, 2012,29(4):196-199.

[12]田淑杭,姜丽娟.一种参数自整定模糊PID控制器的研究[J].电气传动自动化, 2003,25(6):28-30.

[13]骆德渊,刘荣,李纪文.采用模糊逻辑的移动机器人轨迹跟踪[J].电子科技大学学报, 2008,37(6):943-946.

[14]高健,黄心汉,彭刚,等.移动机器人PID运动控制器参数的模糊自整定[J].华中科技大学学报:自然科学版, 2004,32(增刊):48-51.

[15]赵子恺.LEGO机器人的编程控制[J].中国计量学院学报, 2004,15(1):44-48.

[16]宫广骅.玩转乐高机器人[M].北京:人民邮电出版社, 2014.

Fuzzy-PID arithmetic for blind guiding robots

ZHANGZhimei,CHENGLiying,ZHAOYiheng,WUHaiyuan

(College of Physics Science and Technology, Shenyang Normal University, Shenyang 110034, China)

Combining the PID superiority for constant linear systems and effective control of fuzzy controller for complex nonlinear systems, A fuzzy-PID arithmetic was applied in blind guiding robots to realize intelligent tracking and obstacle-avoiding.The blind guiding robot used LEGO robot kit, obstacle-avoid link used ultrasonic sensors to detect obstacles information, the controller collected obstacle information and robot speed information to realize obstacle-avoid by using fuzzy-PID arithmetic.Intelligent tracking used real-time tracking deviation and rate of deviation to modify the PID parameters.The recognition detection used infrared sensors.Final examples show that improved fuzzy PID control arithmetic can greatly increase the accuracy of obstacle avoidance and track accurately.

Fuzzy-PID arithmetic; blind guiding robots; track

2014-09-20。

辽宁省教育厅科学技术研究项目(L2012391)。

张志美(1982-),女,河北尚义人,沈阳师范大学讲师,东北大学博士研究生。

1673-5862(2015)01-0081-05

TP273.4

10.3969/ j.issn.1673-5862.2015.01.018