非连续非拟凹博弈的Nash均衡存在性

张婧宇, 侯吉成

(北京信息科技大学 理学院, 北京 100192)



非连续非拟凹博弈的Nash均衡存在性

张婧宇, 侯吉成

(北京信息科技大学 理学院, 北京 100192)

法国数学家Rabia Nessah于2011年提出了一个Nash均衡存在性定理。该定理证明了对于一个有界的、紧的并且拟凹的广义弱转移连续博弈,一定存在一个Nash均衡。为了提高Nessah的定理的普遍适用性,减弱定理的条件,通过构造一个衡量拟凹程度大小标准的函数,引入了一个新的弱转移连续函数的概念,减弱了Nessah的定理对支付函数拟凹性的设定,并在此基础上得到了一个在非拟凹条件下,判断Nash均衡是否存在的新的定理,结果一般化了Nessah的定理。为寻找Nash均衡增加了新的理论基础和新的方向。

Nash均衡; 广义弱转移连续;α弱转移连续; 拟凹性

0 引 言

研究均衡点的存在性是博弈论的首要问题。1951年,诺贝尔经济学奖获得者Nash对非合作博弈给出了一个均衡点的存在性定理(现在被称为Nash均衡存在性定理)。此后,许多作者建立了许多关于这个定理的更一般形式,但是在这些结论中,都假设了策略空间的凸性,支付函数的连续性和凹性,而这些都是非常强的条件,很多情况下难以满足。

本文主要的目的是去掉非连续博弈Nash均衡存在性定理中拟凹性的假定。近年来,很多文章都致力于减弱博弈中支付函数的连续性条件,如Baye等[1](1993);Tian[2](1995);Reny[3](1999);Bagh等[4](2006);Barelli等[5](2009);Carmona[6](2009);Nessah等[7](2009);McLennan等[8](2011)、Carmona[9](2011)和Nessah[10](2011)。但是,尽管经济问题中实际博弈模型有许多不满足拟凹性,但只有很少的研究者在探讨如何减弱甚至去掉拟凹性假定,特别是对于非连续博弈。

本文为了在比较弱的连续性条件下去掉拟凹性条件,通过使用Philippe在文献[11]中介绍的定量刻画拟凹性的函数ρi:X→R引入一个α弱转移连续函数的概念,然后利用它给出了一个新的没有拟凹性条件的Nash均衡存在性定理。本文的结果一般化了Nessah的定理(文献[10]的定理3.2)。

1 预备知识

如果S是一个集合,则〈S〉表示S的所有非空有限子集构成的集合。设X是一个凸集,f:X→R是一个函数,如果对于任意的x1,x2∈X和任意的λ∈[0,1],都有f(λx1+(1-λ)x2)≥min{f(x1),f(x2)},则称f:X→R是拟凹的[13]。

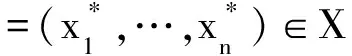
对所有的xi∈Xi都成立,则称x*是此博弈G的一个Nash均衡点。

定义2[14]如果每个局中人i的纯策略集Xi是非空的、紧的、凸的,则称博弈G是紧的。

定义3[15]如果对于任意的i和任意的x-i∈X-i,定义在Xi上的函数ui(•,x-i)是拟凹的,即对任意的x-i∈X-i,函数xiui(xi,x-i)在Xi上是拟凹的,则称博弈G是拟凹的。

定义4[10]如果集值映射C:X→Y是非空、紧值、上半连续的,则称C是行为良好的。

2 衡量拟凹性的标准

为将拟凹性条件减弱,Philippe在文献[11]中引入的一个衡量拟凹程度大小的标准。

为了介绍笔者的结果,下面介绍由Philippe在文献[11]中给出的一个引理和一个定理。

引理1[11]1)ρf≥πf≥0;

2) 若f是有界的,那么ρf也是有界的;

3)f是拟凹的,当且仅当对任意的x∈Y,有ρf(x)=0。

为了更好地理解,介绍下面一个例子。

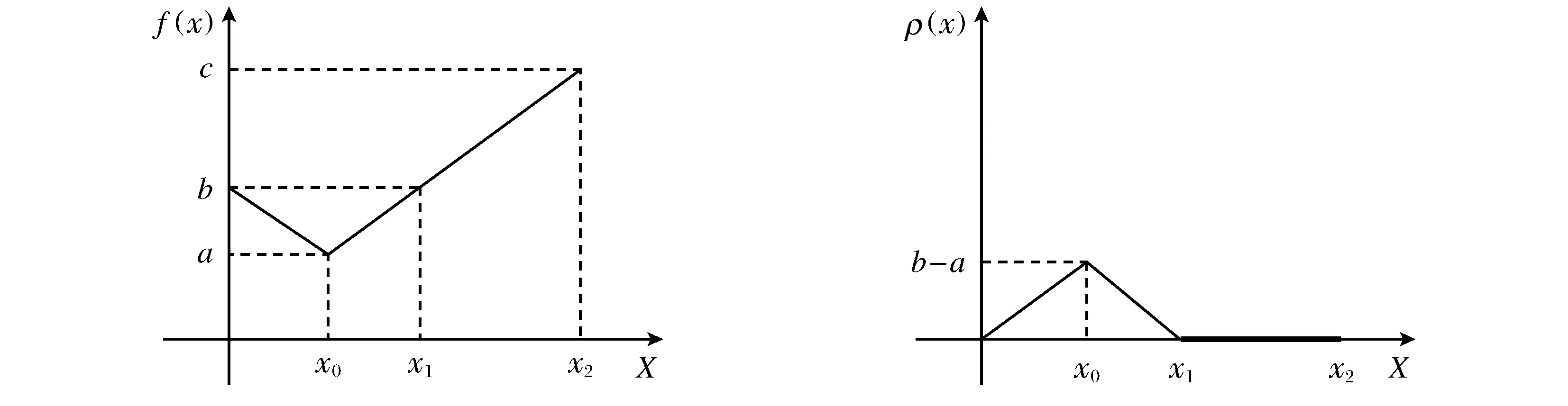
图1 非拟凹函数和拟凹程度函数

如图1所示,在x∈(0,x0)时有

在x∈(x0,x1)时与上面同理有

在x∈(x1,x2)时有

ρ(x)=π(x)=0。

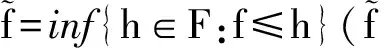
定义5[11]对于每一个i=1,…,n,按照下述,定义ρi:X→R

对于任意的x∈X。显然ρi:X→R是上半连续的。

注:根据引理1,如果G=(Xi,ui)i∈I是拟凹的,那么对于任意的x∈X都有ρi(x)=0,因此这时定义6归于文献[10]的定义3.2并且被称为广义弱转移连续的。

3 主要结论

定理2 如果博弈是有界的、紧的、并且是α弱转移连续的,那么它一定存在一个Nash均衡点。

为了证明定理2,先给出下面的引理。

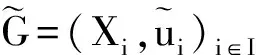
证明 1) 设x∈X是G的一个Nash均衡点,那么对每一个i都有

对每一个yi∈Xi都成立。令{z1,…,zn}∈〈Xi〉和yi∈co{z1,…,zn},有

由定理1可知

由定理1,知

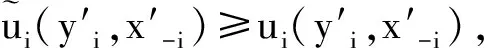
下面给出定理2的证明。

又因为

4 结 语

本文通过引入了一个衡量拟凹程度大小标准的函数,给出一个新的弱转移连续函数的概念,得到了一个新的Nash均衡存在性定理,减弱了拟凹性的假设,为寻找Nash均衡给出了新的方向。

[1]BAYEM,TIANGuoqiang,ZHOUJianxin.Characterizationsoftheexistenceofequilibriaingameswithdiscontinuousandnon-quasiconcavepayoffs[J].RevEconStud, 1993,60(4):925-948.

[2]TIANGuoqiang,ZHOUJianxin.Transfercontinuities,generalizationsoftheWeierstrassandmaximumtheorems:afullcharacterization[J].JMathEcon, 1995,24(3):282-302.

[3]RENYPJ.OntheexistenceofpureandmixedstrategyNashequilibriaindiscontinuousgames[J].Econometrica, 1999,67(5):1029-1056.

[4]BAGHA,JOFREA.Reciprocaluppersemicontinuousandbetterreplysecuregames:acomment[J].Econometrica, 2006,74(6):1715-1721.

[5]BARELLIP,ENEGHELI.Anoteontheequilibriumexistenceproblemindiscontinuousgames[J].Econometrica, 2013,81(2):813-824.

[6]CARMONAG.Anexistenceresultfordiscontinuousgames[J].JEconTheory, 2009,144(3):1333-1340.

[7]NESSAHR,TIANGuoqiang.Exsitenceofsolutionofminimaxinequalities,equlibriaingamesandfixedpointswithoutconvexityandcompactnessassumptions[J].OptimTheoryAppl, 2013,157(1):75-95.

[8]ANDREWM,PAULOKM,RABEET.Gameswithdiscontinuouspayoffs:astrengtheningofReny’sexistencetheorem[J].Econometrica, 2011,79(5):1643-1664.

[9]CARMONAJ.Understandingsomerecentexistenceresultsfordiscontinuousgames[J].EconTheory, 2011,48(1):31-45.

[10]NESSAHR.GeneralizedweaktransfercontinuityandtheNashequilibrium[J].JMathEcon, 2011,47(4/5):659-662.

[11]BICHP.ExistenceofpureNashequilibriaindiscontinuousandnonquasiconcavegames[J].IntJGameTheory, 2009,38(3):395-410.

[12]宋玉清,韩国涛.博弈论中某些概念的辨析[J].辽宁师范大学学报:自然科学版, 2012,35(4):456-462.

[13]愈建.博弈论与非线性分析绪论[M].北京:科学出版社, 2011.

[14]谢识予.经济博弈论[M].2版.上海:复旦大学出版社, 2002.

[15]MUNKRESSJR.拓扑学[M].熊金城,译.北京:机械工程出版社, 2006.

Existence of Nash equilibrium in discontinuous and non quasiconcave games

ZHANGJingyu,HOUJicheng

(School of Applied Science, Beijing Information Science & Technology University, Beijing 100192, China)

In 2011, the French mathematician Rabia Nessah proposed a Nash equilibrium existence theorem.The theorem has proved that a bounded, compact quasiconcave and generalized weak transfer continuous game has a Nash equilibrium certainly.In order to improve universal applicability of the Nessah’s theorem and reduce the theorem’s conditions, the author introduces a new concept called asα-weakly transfer continuous to reduce the assumption of quasicancavity of payoff functions in Nessah’s theorem by constructing a new function of measuring the degree of quasiconcavity.On this basis the author obtains a new theorem of the existence of Nash equilibrium under the condition of nonquasiconcavity.The result generalizes Nessah’s theorem mentioned above.It adds a new theoretical basis and direction for looking for Nash equilibrium.

Nash equilibrium; generalized weakly transfer continuous;α-weakly transfer continuous; quasiconcavity

2014-06-07。

国家自然科学基金资助项目(11271178)。

张婧宇(1991-),女(满族),内蒙古通辽人,北京信息科技大学硕士研究生; 通信作者: 侯吉成(1963-),男,吉林九台人,北京信息科技大学教授,博士,硕士研究生导师。

1673-5862(2015)01-0043-04

O225

A

10.3969/ j.issn.1673-5862.2015.01.010