液压挖掘机动臂能量回收单元分析与研究
2015-04-20黄鲲
黄鲲
摘 要:针对液压挖掘机动臂电气式能量回收系统的结构,以液压马达-发电机单元作为其能量回收单元,建立了能量回收单元的数学模型,提出了能量回收单元的转速控制方法;考虑到液压马达入口压力的变化,引入了扰动补偿以提高系统的抗干扰能力;在此基础上建立了相应的传递函数模型,并对设计的控制方法进行了仿真研究。研究结果表明:液压马达-发电机单元是影响动臂能量回收性能的关键部分;所设计的控制方法具有理想的动态性能和稳态精度;控制系统采用扰动补偿后转速波动可下降50%左右,能量回收单元的抗干扰性能得到较好的改善。
关键词:液压挖掘机;动臂;能量回收;液压马达;发电机
1 概述
21世纪以来,全世界范围内的能源危机和环境问题日益加剧,液压挖掘机作为工程机械建设中的主要施工机械,它的高油耗、差排放和高污染等缺点,迫使其得到了广泛关注[1]。液压挖掘机各执行机构的负载惯性较大,各机械臂的上下摆动比较频繁,在机械臂下放制动时,具有很大的势能,因此在动臂下降的过程中,大量的势能转化为热能消耗在动臂主控阀的单向节流孔上。所以,对动臂势能的回收具有重大意义[2]。目前国内外对挖掘机动臂势能的回收利用已做了大量研究,并取得了一些成果[3]。由于混合动力在汽车上的成功运用[4],对于挖掘机的混合动力研究也在进行中[5-8]。其中以电气式混合动力回收尤为突出,即将动臂下降释放的势能通过发电装置转化为电能并储存,其能量再利用的方式比较灵活,为混合动力系统提供电能储存的蓄电池或者是超级电容可以将回收的能量直接用于驱动各种用电器。对于电气式能量回收系统,通常采用液压马达-发电机单元作为能量回收单元。因此,能量回收单元的参数设定及建模分析对能量回收具有重大意义,对此也有学者进行了研究[9-10]。文章针对液压挖掘机电气式能量回收系统的结构,以液压马达-发电机单元作为能量回收单元,建立了能量回收单元的数学模型,提出了能量回收单元的转速控制方法,考虑到液压马达入口压力的变化,引入了扰动补偿以提高系统的抗干扰能力,在此基础上建立了相应的仿真模型,并对设计的控制方法进行了仿真研究。
2 能量回收系统结构
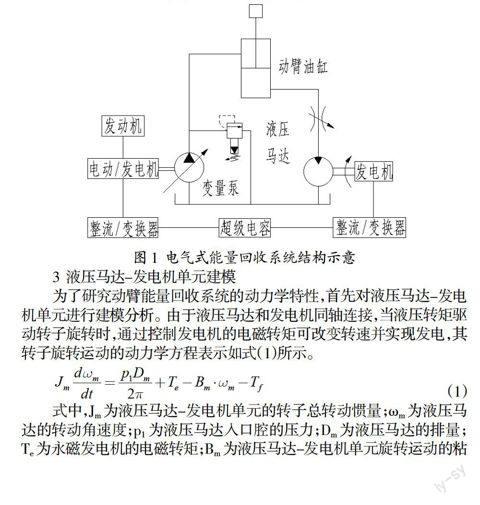
电气式混合动力液压挖掘机动臂能量回收系统的结构如图1所示。其中液压马达选择定量柱塞马达,发电机选择由变频器控制的永磁发电机,储能元件采用适应大电流充放电的超级电容。当动臂液压缸向下运动时,在液压缸无杆腔产生的压力油经节流阀驱动液压马达-发电机单元工作,再由变频器将回收的能量转化为匹配的直流电并储存在超级电容中。动臂下降过程通过调节节流阀的阀芯位移和发电机的电流共同完成,利用两者的高效配合获得理想的操作性能。对于混合动力液压挖掘机,采用液压马达-发电机单元构成的电气式能量回收系统对动臂势能进行回收再利用,是改善挖掘机能量损失的有效途径。
图1 电气式能量回收系统结构示意
3 液壓马达-发电机单元建模
为了研究动臂能量回收系统的动力学特性,首先对液压马达-发电机单元进行建模分析。由于液压马达和发电机同轴连接,当液压转矩驱动转子旋转时,通过控制发电机的电磁转矩可改变转速并实现发电,其转子旋转运动的动力学方程表示如式(1)所示。
(1)
式中,Jm为液压马达-发电机单元的转子总转动惯量;?棕m为液压马达的转动角速度;p1为液压马达入口腔的压力;Dm为液压马达的排量;Te为永磁发电机的电磁转矩;Bm为液压马达-发电机单元旋转运动的粘滞阻尼系数;Tf为液压马达-发电机单元旋转运动的摩擦转矩。对式(1)做拉氏变换,可以得到该环节的传递函数如式(2)所示:
(2)
相比于机械系统的时间常数,编码器转速反馈的频率响应可以看成是比例环节,与此同时液压马达-发电机单元的转速控制等价于一阶系统,因此可以采用PI控制器来实现无差控制。转速PI控制器的输出如式(3)所示:
(3)
式中,KP为转速PI控制器的比例系数;Ki为转速PI控制器的积分系数;?棕m*为发电机的目标转速。由于液压马达的入口压力通常在大范围内波动,这对系统的抗干扰能力提出了较高的要求。为了保证系统在输入变化时仍保持良好的速度控制性能,控制器采用扰动估计并进行补偿的方法,根据转子动力学方程,液压马达输出轴的驱动转矩可估计如式(4)所示:
(4)
式中,Gl(s)为一阶低通滤波器。
在PI调节的基础上,可以利用液压马达驱动转矩的估计值构建扰动补偿。根据发电机转子旋转运动的动力学方程,液压马达入口的压力估计如式(5)所示:
(5)
由于负载可测,所以液压马达的泄漏量可以表示为式(6):
(6)
式(6)中,C(?棕m)为液压马达的泄漏系数。
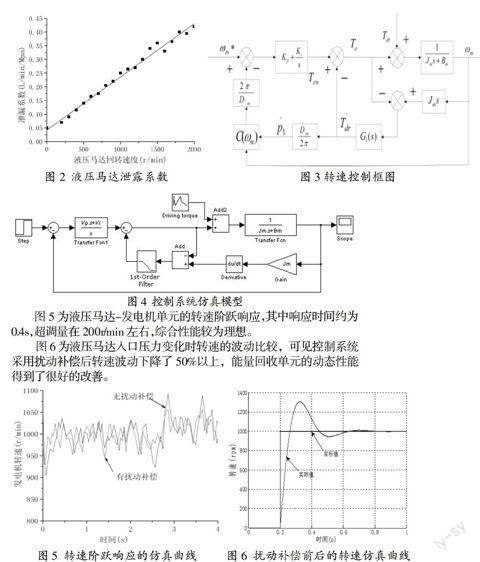
图2是液压马达在不同转速下测量得到的泄漏系数。计算时可以通过查阅图2得到。
液压马达的泄漏补偿估计为式(7)所示:
(7)
从式(7)可以看出,当转速足够小时液压马达的泄漏补偿值将会变为0。
根据公式(1)-(7)得到发电机转速控制框图,根据图3所示,可以得到转速控制系统的闭环传递函数,如式(8)所示:
(8)
与此同时,液压马达-发电机单元实际转速对扰动量的传递函数表示如式(9)所示:
(9)
由于液压马达的转矩变化通常表现在低频段,此时一阶低通滤波器趋向于1,代入式(9)后,可以得出转速对扰动量的传递函数趋向于0。因此,控制系统采用扰动补偿后,扰动量对转速控制的影响将有效降低。
4 仿真研究
根据控制系统的结构和参数,建立如图4所示的仿真模型。仿真环境为Matlab/Simulink。
图4 控制系统仿真模型
图5为液压马达-发电机单元的转速阶跃响应,其中响应时间约为0.4s,超调量在200r/min左右,综合性能较为理想。
图6为液压马达入口压力变化时转速的波动比较,可见控制系统采用扰动补偿后转速波动下降了50%以上,能量回收单元的动态性能得到了很好的改善。
5 结束语
针对混合动力液压挖掘机,液压马达-发电机单元是影响动臂能量回收性能的关键部分,是改善挖掘机能量损失的有效途径。仿真结果表明,所设计的控制方法具有理想的动态性能和稳态精度。控制系统采用扰动补偿后转速波动可下降50%左右,能量回收单元的抗干扰性能得到较好的改善。文中只针对液压马达-发电机单元进行了研究,并未涉及实际操作中能量回收系统整体的性能。因此,这将是电气式能量回收系统研究的一个重点。
参考文献
[1]张彦廷.基于混合动力与能量回收的液压挖掘机节能研究[D].浙江大学,2006,6.
[2]張彦廷,王庆丰,肖清.混合动力液压挖掘机液压马达的能量回收及试验[J].机械工程学报,2007,43(8):218-223.
[3]裴磊,管成,邱清盈.混合动力挖掘机动臂势能回收研究[J].机床与液压,2009,37(3):64-67.
[4]郝志勇,岳东鹏,李建国.混合动力汽车研究的现状及未来发展前景[J].铁道机动车辆,2003,23(1):205-210.
[5]肖清,王庆丰.混合动力液压挖掘机动力系统的参数匹配方法[J].中国公路学报,2008,21(1):121-126.
[6]LIN Tian-liang,WANG Qing-feng,HU Bao-zan,et al.Development of Hybrid Powered Hydraulic Construction Machinery [J].Automation in Construction,2010,19(1):11-19.
[7]XIAO Qing,WANG Qingfeng,ZHANG Yan-ting. Control Strategies of Power System in Hydraulic Excavator[J].Automation in Construction, 2008,17(4):361-367.
[8]Tao Wang, Qingfeng Wang, Tianliang Lin. Improvement of boom control performance for hybrid hydraulic excavator with potential energy recovery[J].Automation in Construction,2013,30:161-169.
[9]林潇,管成,裴磊,等.混合动力液压挖掘机动臂势能回收系统[J].农业机械学报,2009,40(4):96-101.
[10]T.Lin,Q. Wang,B.Hu and W. Gong. Research on the energy regeneration systems for hybrid hydraulic excavators[J].Automation in Construction,2010,19(8):1016-1026.