一种高分辨率3维图像的自适应降噪算法

向志聪，张程潇，白玉磊，赖文敬，王钦若，周延周

(广东工业大学自动化学院，广州510006)

引 言

随着激光机器视觉技术在工业生产中的迅速发展，在3维自然纹理［1-2］立体印刷方面，物体表面3维轮廓测量技术应用广泛。所谓3维自然纹理主要指各种木材纹理、皮革纹理、甚至是人工的油画纹理。将这些3维纹理高保真地印刷在壁纸、墙纸、家具贴纸、瓷砖和纺织服装制品上，就是立体印刷。作为平面印刷的升级产业，立体印刷的市场需求大，产业利润高，是现代化的高精尖产业。由于立体印刷对丰富的细节要求更为严格，一般要求x，y方向的测量分辨率高(每英寸点数(dots per inch，DPI)大于1000)和z方向的测量精度高(小于±5μm)，本实验中系统采用的高精度相机镜头，并减少镜头视场范围至23mm，x和y方向的测量分辨率可高达到1700DPI。因此本文中实验系统的3维数据采集精度很高，进行3维数据采集时，难免会存在一些噪声信息，这时就需要对3维图像进行滤波处理。传统的滤波方法有很多，如中值滤波、均值滤波、小波变换降噪等［3-4］，虽然这些方法也能有效地去除噪点，但是往往也会去除有用的3维图像细节信息，使得3维图像失真。

3维图像表示图像中每个像素点都包含空间里3个维度的信息，而3维图像则表示每个像素点只包含空间里两个维度的信息。以3维灰度图像和2维灰度图像为例，普遍意义下，图像中都包含x和y方向的信息，主要的区别在于3维灰度图像中像素点的灰度值则表示被测点z方向的信息，而2维灰度图像中像素点的灰度值不表示被测点z方向的信息，因此3维灰度图像和2维灰度图像存在一定差异，图像降噪方法也有所差异。

近年来，传统的滤波算法也有较大的改进，出现了如自适应小波变换降噪［5］、非局部均值降噪［6-7］等滤波算法，但这些算法运用到立体印刷行业上也难以满足印刷精度的需求。针对立体印刷行业高分辨率3维图像的滤波问题，本文中提出一种基于空间域的高保真自适应降噪算法，该算法既能保留高分辨率图像的边缘、细节等信息［8-9］，也能有效去除3维图像的噪点。因为3维灰度图像和2维灰度图像中的边缘信息和噪声信息的空间域表现形式大致相同，所以本文中降噪算法可通用。因此，本文中提出的高保真自适应降噪算法在自然纹理样品的扫描方面具有广阔的应用前景。

1 实验系统

本文中所使用的线激光实验系统构成如下:线宽为10μm的线激光激光器、SICK公司的Ranger Studio D50 3维相机(连续拍摄速度为1000次/s)、直线步进电机(行程0mm～450mm，重复定位精度5μm)、计算机、运动控制器组成。该线激光实验系统采集的高分辨率3维图像具有x和y方向像素点阵分辨率高，3维测量的z方向测量精度高，3维图像细节丰富等优点。实验系统结构如图1所示。其中相机为互补金属氧化物半导体(complementary metal-oxide semiconductor，CMOS)相机。

Fig.1 System configuration

实验中系统所采用的是基于线激光与3维相机组成的三角测量高度方法［10-11］。三角法测量高度原理就是当一束线激光投射在被测样品表面，原来平直的线激光被物体表面轮廓高低所改变，最终在3维相机的像平面上的成像也发生相应的位移。通过计算3维相机成像位移的大小，可以得出物体表面的实际高度信息，激光器和3维相机组成的测量结构如图2所示。

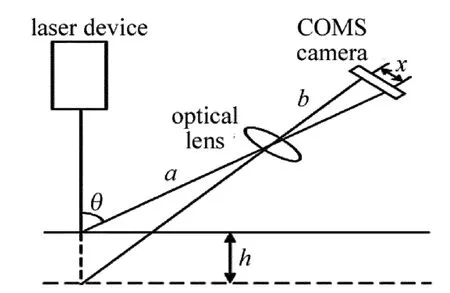
Fig.2 Triangulation measurement of laser

假设线激光中某一光点在CMOS相机像平面上的成像位移为x，由下式可计算出被测样品表面上该点的实际高度差:

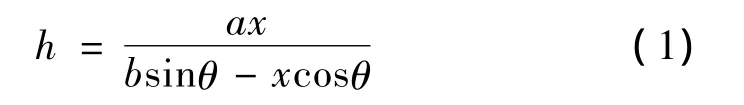
式中，a为3维相机物距;b为3维相机像距;θ为激光器中轴与相机中轴之间的夹角。

2 自适应降噪算法

2.1 噪点的形成

在现实工业生产中，因受到成像装置和外部环境的干扰，如3维相机曝光时间、光照强度等因素影响，3维图像会含有一定的噪声信息。这些噪声干扰信息会造成3维图像的成像质量下降，影响人们对3维图像的观察和应用。因此，需要把噪声信息从3维图像有效图像信息中分离出来，这就称为图像降噪。图像降噪的主要目的在于尽可能多地检测图像的细节、边缘，保留原始图像的细节、边缘等具体信息的同时，去除图像中的噪声信息，还原物体的真实面貌。本文中以花草自然纹理皮革材料为被测物，实物图如图3所示。实验中测量皮革材料的表面轮廓数据所得的部分噪点图像，如图4所示。

Fig.3 Natural texture of leather material of flowers

在完成高分辨率的3维图像数据采集后，必须在保存3维图像边缘、细节部分的条件下，去除3维图像中的噪声信息。实验中所得到3维图像是灰度图像，Z表示z方向的灰度大小，3维图像的灰度从黑到白分为0～255，即当灰度值为0时，在图像中呈黑色，表示z方向最小值，当灰度值为255时，在图像中呈白色，表示z方向最大值。

Fig.4 Noisy point

一般情况下，在3维测量过程中容易产生两种噪点:一种是Z值极大的点，在图像上呈白色，产生的原因是相机曝光时间过大，使COMS相机由于内部电路产生的噪声点显现出来;另一种是Z值极小的点，在图像上呈深黑色，产生的原因是曝光时间不足或者光路被物体所遮盖所致。

2.2 搜索噪声

搜索噪声主要采用循环的动态阈值比较法，即噪声搜索窗口循环调整窗口阶数，并对噪声进行搜索。本文中3维图像以像素点为考察对象，不同的灰度值对应着不同的z方向数值，即表示该点高度值。首先对3维图像预处理，去除毛刺噪声，可建立一个与3维图像矩阵大小一致的零矩阵，记为M，用于记录噪点的位置。然后求取3维图像z方向数据的平均值Zm，若像素点的Z值减去这个均值Zm后，所得结果的绝对值大于设定的阈值V，则将对应像素点判定为坏点，M矩阵相应的位置的元素置1。

3维图像预处理后，循环使用不同阶数的搜索窗口对3维图像的各像素点进行噪点判断搜索，搜索3维图像的噪点位置，噪点判断的方法是根据不同阶数搜索窗口的动态阈值［12-13］，若某一像素点的灰度值与搜索窗口内均值的差值大于该动态阈值，则将该像素点判断为噪点，则在M矩阵相应的位置的元素置1，M矩阵已置1的像素点则不进行上述处理。

在本文实验中，所测量的样本为3维自然纹理的皮革材料，假设3维皮革图片的灰度值标准差为σ，则3维图像预处理的毛刺噪声阈值V设定为3σ。扫描整幅3维图片，若某一像素的灰度值与图像灰度均值的差值大于此阈值V，则判定此点为噪点，M矩阵相应的位置的元素置1，预处理的噪点判定公式如下:

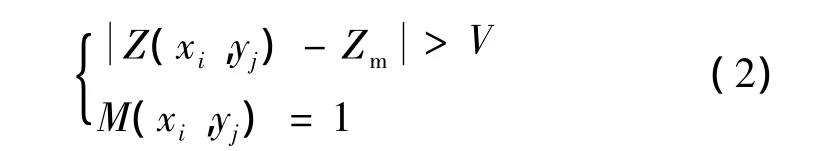
式中，Z(xi，yj)表示某一像素点的灰度值，Zm表示图像灰度均值。

完成上述步骤后，此时m阶动态窗口由3×3变化到15×15，对3维图像循环使用不同阶数的窗口进行噪点搜索。搜索窗口搜索噪点的方法是使用搜索窗口中心点的值与窗口里其它点的值进行比较，若比较值大于某一阈值，则将该点判定为R点，否则为S点，设窗口内除去中心点后的标准差为σ，则此搜索窗口的动态阈值Vb为3σ，则R点判定由下式可得:

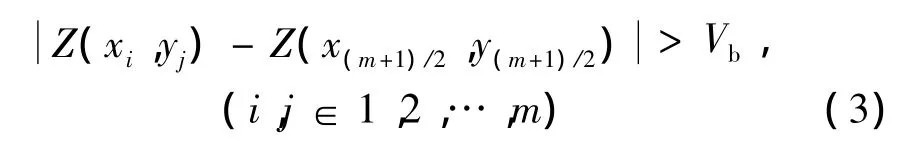
若R点数量大于S点数量，则将此搜索窗口的中心点判定为噪点，M矩阵相应的位置的元素置1，对M矩阵已置1的像素点不进行上述处理。

假设边缘点R的数量NR，边缘点S的数量NS，以3阶搜索窗口为例，如图5所示。

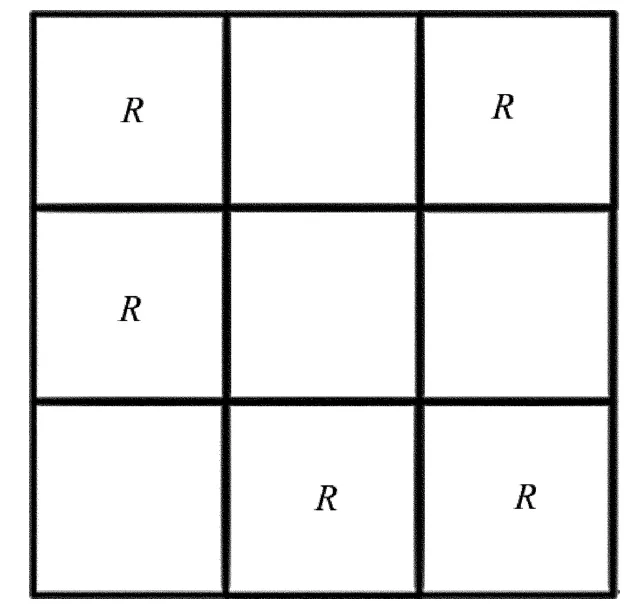
Fig.5 Third-order search window

由图5可得，3阶窗口边缘点R的数量NR=5，边缘点S的数量NS=3，则窗口中心点A的噪声判定可由下式可得:

单次m阶动态搜索窗口循环搜索后，搜索窗口由左至右，由上至下逐步移动，每次移动一列(行)像素，移动后继续进行上述比较，继续进行上述噪声比较，M矩阵已置1的像素点不进行上述处理。最后可得到M矩阵，M矩阵中置1元素则对应着3维图像的噪声位置。

2.3 对噪声滤波

传统滤波方法中，以空间域的均值滤波、中值滤波最为经典，但是空间域滤波方法对窗口的选用存在很大的依赖性，若滤波窗口较小，则窗口内噪点较多，不利于滤波处理，若滤波窗口较大，滤波处理后的值与噪声真实值存在较大差异。

作者提出的噪声滤波方法是一种自适应的均值滤波方法，即滤波窗口可自动调整窗口阶数大小，并对采用最佳的滤波窗口对窗口内的中心噪声进行均值滤波处理。具体的噪声滤波方法是:得到M矩阵后，M矩阵中置1元素则对应着3维图像的噪声位置，然后m阶动态滤波窗口由3×3变化到15×15，若搜索窗口内的正常像素数量大于噪点像素数量时，则使用该滤波窗口对该窗口的中心噪点进行均值滤波处理，否则滤波窗口阶数增加，再进行上述判断，直至窗口内的正常像素数量大于噪点像素数量，再使用该滤波窗口对该窗口的中心噪点进行均值滤波处理。以3阶滤波处理为例，如图6所示。

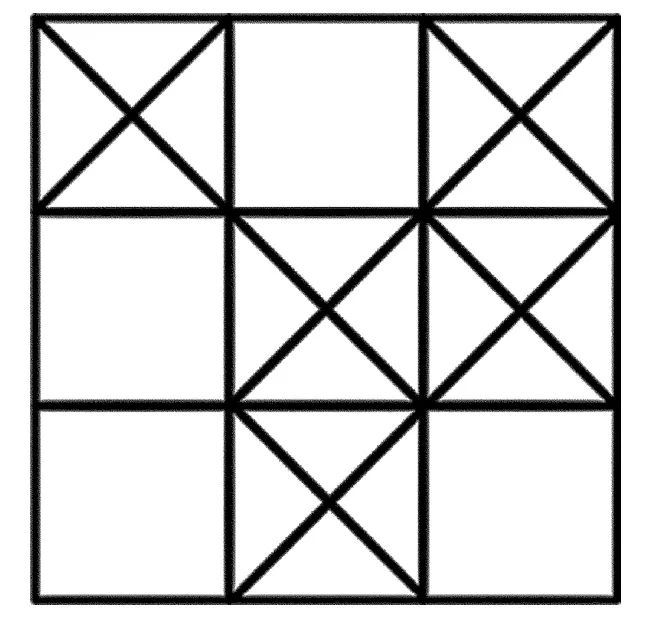
Fig.6 Third-order filter window

在图6中，在以噪点为中心的3×3滤波窗口内，在边缘的8个像素点中，标记的像素点为噪点，其数量Nn=4，未标记的像素点为正常像素点，其数量Na=4。因为窗口内的正常像素数量不大于噪点像素数量，所以不能使用3×3滤波窗口对该窗口的中心噪点进行滤波处理。此时，滤波窗口阶数增加，变为5×5滤波窗口，如图7所示。

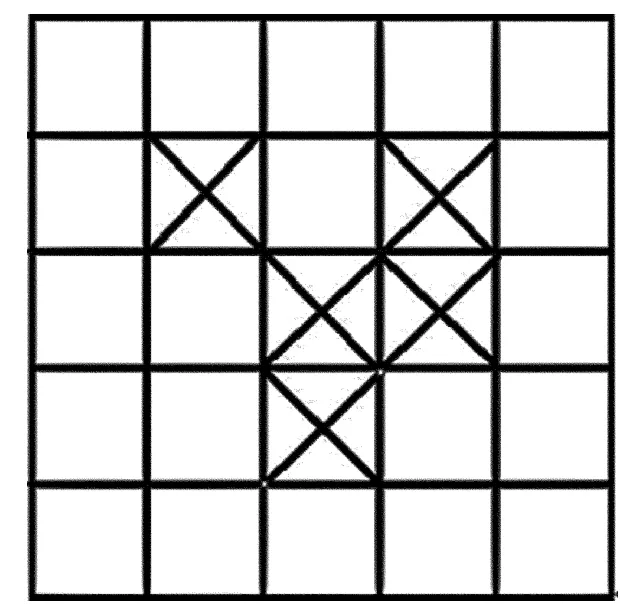
Fig.7 Fifth-order filter window

在图7中，在以噪点为中心的5×5滤波窗口内，在边缘的24个像素点中，标记的像素点为噪点，其数量Nn=4，未标记的像素点为正常像素点，其数量Na=20，因为窗口内的正常像素数量大于噪点像素数量，所以能使用5×5滤波窗口对该窗口的中心噪点进行滤波处理。对滤波窗口边缘的正常像素点的灰度求均值，然后将所求得的值替代中心的噪点值，正常值不变，如果边缘点也有噪点，则将此噪点的灰度值取零，滤波后的噪点灰度值为:

式中，m为滤波窗口阶数，Nn为边缘噪点数。本例中m=5，Nn=4，Z(x(m+1)/2，y(m+1)/2)为噪点的高度值。

因此，作者提出的自适应均值降噪算法，能循环变化噪点搜索窗口的阶数，并采用动态阈值法对噪声搜索，也能自动调整滤波窗口阶数，并采用最佳的滤波窗口对窗口中心噪声点进行均值滤波。对比传统的均值滤波，本文中提出的自适应降噪算法克服了对窗口阶数的依赖，是一种较好的滤波方法。

3 实验结果

在实验中，以3维纹理的皮革材料为被测物体，通过拍摄测量两组皮革材料不同部位的表面轮廓数据，以作者提出的高保真自适应降噪算法对实验所得的高分辨率图片(大于1700DPI)进行滤波处理，并与传统的均值降噪、小波变换降噪的降噪效果进行对比，得到如图8所示的实验效果图，其中图8a～图8d为第1组，图8e～图8h为第2组。

通过本文中的降噪算法与均值降噪算法、小波降噪算法进行对比。图8中区域A表示3维图像噪点区域，可明显看出，均值降噪(见图8b和图8f)和本文中自适应降噪(见图8d和图8h)的区域A中，降噪效果相当，平滑效果较好;小波降噪效果(见图8c和图8g)次之，仍存在部分噪声。区域B表示3维图像边缘区域。均值降噪效果图中(见图8b和图8f)，由于均值滤波造成图像边缘钝化，细节模糊不清;小波降噪效果图中(见图8c和图8g)，图像细节得以保存，边缘效果较好;自适应降噪效果图中(见图8d和图8h)，更多图像细节部分得以保存，边缘效果最好。从实验结果来看，本文中提出的自适应降噪算法降噪效果比较好，对噪点滤波明显，平滑效果较好，也能较好保留图像的边缘、细节等信息，能满足立体印刷精度的要求。

Fig.8 Partial denoising effect of natural texture of flowers leather

4 结论

提出了一种针对高分辨率3维图像的自适应滤波方法。该方法利用动态搜索窗口，根据该动态搜索窗口的阈值，寻找图像中的噪点，并自动选择最佳的滤波窗口对噪点进行均值滤波。最后对该滤波方法进行检验，并将本文中提出的降噪算法的降噪效果与均值降噪算法、小波降噪算法的降噪效果进行对比，对比结果中发现，本文中提出的降噪算法既可保存图像的边缘、细节部分信息，也可在噪点处实现平滑处理，对图像的降噪效果较好，高分辨率图像不失真，从而很好解决了立体印刷行业对3维立体扫描数据的高精度要求这一大难题。

［1］ OJALA T，PIETIKAINEN M.Multiresolution gray-scale and rotation invariant texture classification with local binary patterns［J］.IEEE Pattern Analysis and Machine Intelligence，2002，24(7):971-987.

［2］ HE F Q，WANG W，CHEN Z C.Automatic visual inspection for leather manufacture［J］.Key Engineering Materials，2006，326/328:469-472.

［3］ GUPTA G.Algorithm for image processing using improved median filter and comparison of mean，median and improved median filter［J］.International Journal of Soft Computing and Engineering，2011，1(5):2231-2307.

［4］ BULTHEEL A.Empirical Bayes approach to improve wavelet thresholding for image noise reduction［J］.Journal of the American Statistical Association，2001，96(454):629-639.

［5］ CHANG S G，YU B，VETTERLI M.Adaptive wavelet thresholding for image denoising and compression［J］.IEEE Image Processing，2000，9(9):1532-1546.

［6］ LIU Y L，WANG J，CHEN X，et al.A robust and fast non-local means algorithm for image denoising［J］.Journal of Computer Science and Technology，2008，23(2):270-279.

［7］ SALMON J.Two parameters for denoising with non-local means［J］.IEEE Signal Processing Letters，2010，17(3):269-272.

［8］ RAGHAVAN U N，ALBERT R，KUMARA S.Near linear time algorithm to detect community structures in large-scale networks［J］.Physical Review，2007，E76(3):036106.

［9］ MARTIN D R，FOWLKES C C，MALIK J.Learning to detect natural image boundaries using local brightness，color，and texture cues［J］.IEEE Pattern Analysis and Machine Intelligence，2004，26(5):530-549.

［10］ WANG Ch，ZHAO B.Research of thin plate thickness measurement based on single lens laser triangulation ［J］.Laser Technology，2013，37(1):6-10(in Chinese).

［11］ ZHANG H X.Study on building modeling based on 3-D laser scanning technology［J］.Laser Technology，2014，38(3):431-434(in Chinese).

［12］ GAL Y，MEHNERT A J H，BRADLEY A P，et al.Denoising of dynamic contrast-enhanced MR images using dynamic nonlocal means［J］.IEEE Medical Imaging，2010，29(2):302-310.

［13］ CAI T，ZHU J.Adaptive selection of optimal decomposition level in threshold de-noising algorithm based on wavelet［J］.Control and Decision，2006，21(2):217.