楔形微纳光纤能量分布特性研究

章 玲，曾 燕，陈国庆*，周 爱

(1.江南大学理学院，无锡214122;2.哈尔滨工程大学理学院，哈尔滨150001)

引 言

随着光纤器件技术［1-2］的成熟和应用，人们开始深入研究微纳光纤及不同端面结构的光纤特性［3-6］。特殊的微纳光纤尖端结构能够被应用于高灵敏度的光纤传感器、光纤分配器与特种光纤耦合器［7-9］。以往对微纳光纤端面结构特性的研究主要集中在锥形微纳光纤［10-13］，而对其它形状的端面结构特性只有粗略的阐述。楔形是光纤端面典型的形状之一，在半导体激光器与单模光纤的耦合中，楔形端头能够抵消半导体激光器输出椭圆形光斑而导致的高耦合损耗。对楔形微纳光纤的详细研究，将为其在光纤传感器、光纤耦合器等领域的应用打下基础。

基于此，本文中应用COMSOL软件对楔形微纳光纤的特性进行了仿真模拟与数值计算，获得了楔形微纳光纤的能量分布和传输特性，以及楔形微纳光纤发生耦合时的能量分布与耦合效率。

1 楔形微纳光纤模型

1.1 模型结构

楔形微纳光纤是光纤端面和光纤轴线呈某一角度，光纤的纤芯直径将沿着轴线方向逐渐的减小，其模型如图1a所示。作为本文中的研究对象，设纤芯的材料为二氧化硅，其折射率n1=1.45，直径 Φ =1μm，包层材料设为无限大的空气层，其折射率n2=1。微纳光纤的圆柱形部分长度L2=7.5μm，楔形部分长度为L1=7.5μm。D(0μm≤D≤1μm)为微纳光纤楔形部分的斜面到纤芯边沿的长度，定义为微纳楔形光纤楔形部分的有效直径。z=0μm为光纤的纤芯轴线位置。光场从光纤的左端入射，入射光波长为1.55μm。

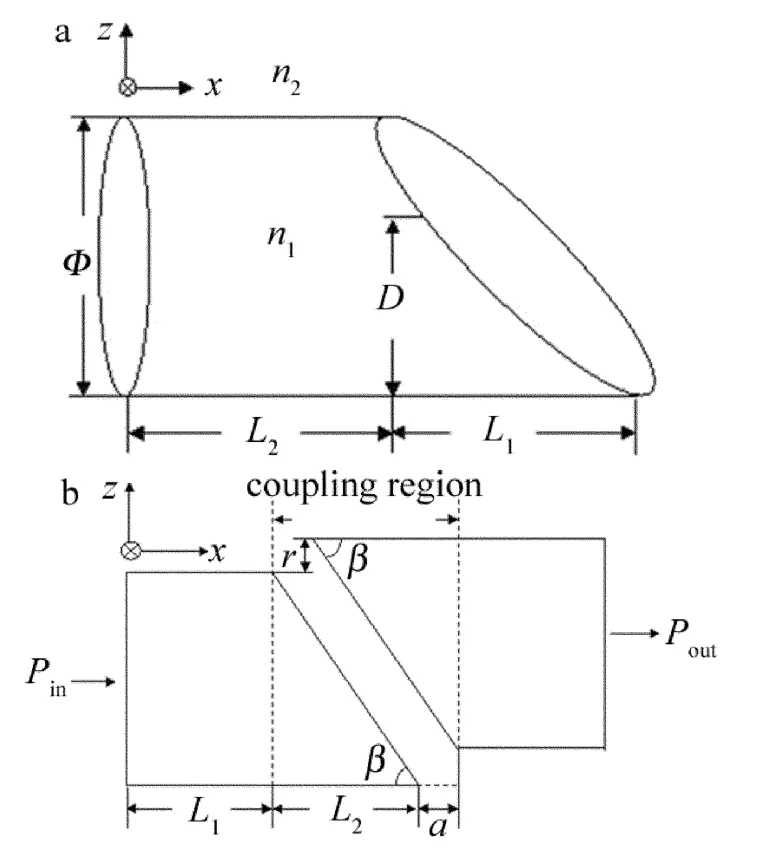
Fig.1 Model of wedge-shaped micro/nano fiber and coupling structure

两根楔形微纳光纤进行耦合的模型如图1b所示，这两根光纤的参量与前述单根楔形微纳光纤的一致，两根光纤之间的轴向位移为a，径向位移为r，β为楔形微纳光纤的楔角，光场从左端输入，右端输出。

1.2 基础方法

对于普通光纤，通常用弱波导近似分析其光学传输特性，而研究纤芯与包层的折射率相差较大的微纳光纤，弱波导近似解不再适用。对于微纳光学，其理论基础仍然是麦克斯韦电磁理论［14］，所以楔形微纳光纤的仿真数学本质仍然是对麦克斯韦方程组的精确求解，而COMSOL正是基于有限元算法的偏微分方程求解数值软件。本文中就是利用COMSOL仿真软件中射频(radio frequency，RF)模块来完成楔形微纳光纤的仿真模拟。

在COMSOL的RF模块计算中，令:

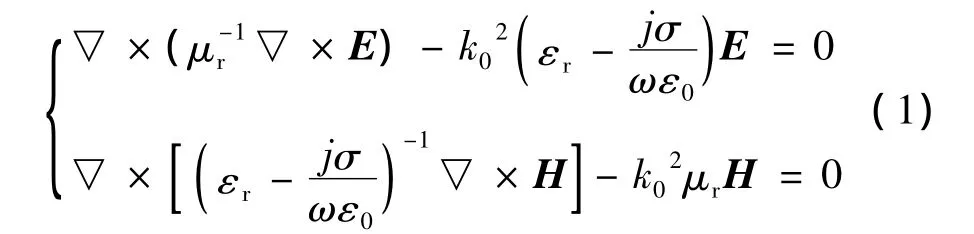
式中，j为电流密度，σ为电导率，μr是相对磁导率，E是电场矢量，H是磁场矢量，εr是相对介电常数，ε0是真空介电常数，k0是真空波数。研究中设置端口边界条件和散射边界条件分别为:

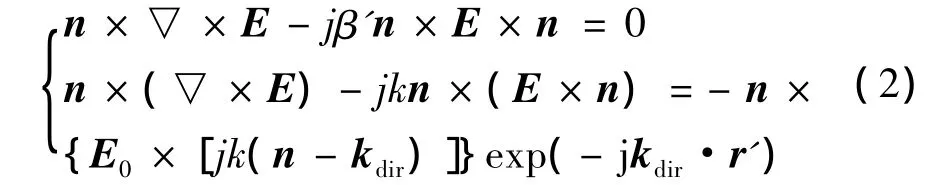
式中，β'为光纤的传播常数，k是波数，n为电场法线矢量，kdir为入射波矢量，r'为光纤z-x面半径矢量。在n×E=0进行楔形微纳光纤的频域分析和模式分析。

在得到能量的分布模拟结果后，本文中主要通过分析光纤中的能量密度情况来研究楔形微纳光纤的能量传输问题。电场能量和磁场能量的定义为:

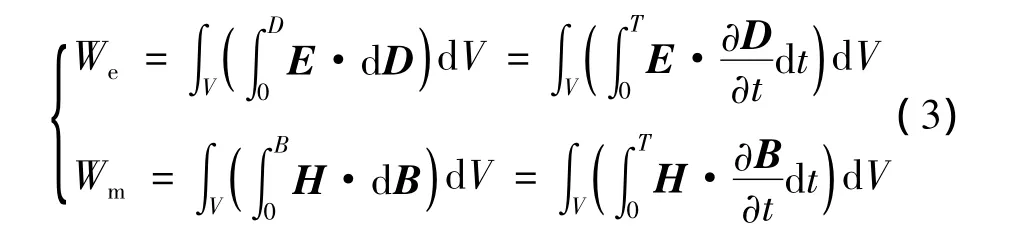
式中，T是时间，D是电感强度，B是磁感强度，下标e和m分别对应电场和磁场，可以得到单位时间内电场能量和磁场能量为:

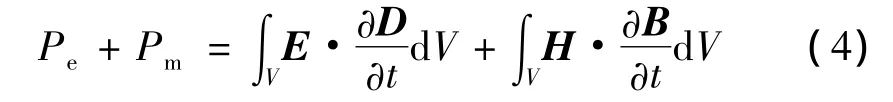
由于传输过程中必然伴随着能量损失，通过波印廷定理［15］可得:

式中，S为封闭曲面，V为S所包围的体积，E×H为波印廷矢量。假设材料是各向同性和线性的，那么:

式中，ε是介电常数，μ是磁导率。对(3)式、(4)式进行积分互换与整合可得:

2 模拟计算与结果分析

2.1 楔形微纳光纤传输特性

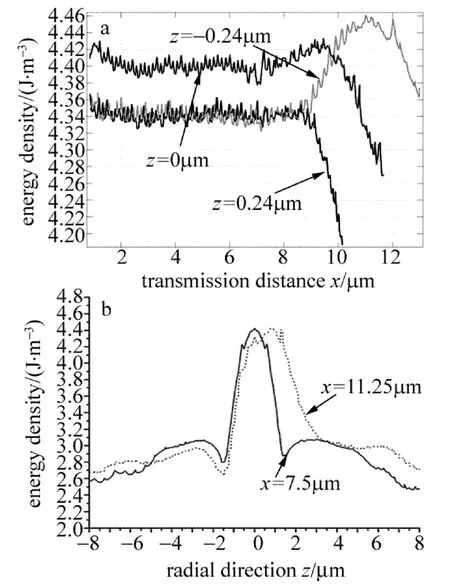
Fig.2 Density distribution of wedge-shape micro/nano fiber

图2a是在楔形微纳光纤的z-x截面中，z=0.24μm，z= －0.24μm两条与轴线(z=0μm)平行的直线上能量密度与传输距离的关系。横坐标x为传输距离，纵坐标为能量密度，3条曲线分别是楔形光纤z=0.24μm，z=0μm，z= －0.24μm 线上的能量密度变化图。可以看到，在传输距离x=7.5μm位置之前，即楔形微纳光纤的圆柱形部分，由于光纤的对称性，z=0.24μm时的曲线和z= －0.24μm 时的曲线基本重合，而z=0μm时的曲线则要在z=0.24μm时的曲线和z=－0.24μm时的曲线之上，但曲线形状几乎一样。这说明了在圆柱形光纤部分，其能量分布并未受到楔形部分的影响，即光纤中的能量主要集中在纤芯部分，距纤芯中心等距离处的能量分布几乎一样。当传输距离x＞7.5μm后，能量开始传输进入楔形光纤部分，图中z=0μm时的曲线和z=0.24μm时的曲线均出现下降趋势，而z=－0.24μm时的曲线却是先增大而后才出现下降。这表明能量在刚进入楔形部分时，其分布就发生了变化，当传输距离大于7.5μm时，部分纤芯被切除，于是随着传输距离的增大，z=0.24μm的位置会最先处于包层中，致使其能量值以较快的速度下降。而在光纤轴线z=0μm的下方，开始时纤芯对能量仍有较强的束缚，且纤芯的体积又小于圆柱形光纤纤芯体积，于是能量密度开始是增大，而后，由于楔形部分有效直径D的减小，光纤束缚光场的能力减弱，能量溢出纤芯产生损耗，导致能量密度出现下降。图2b是楔形光纤横截面的光场分布，图中实线为对应图2a中传输距离x=7.5μm位置，虚线则对应x=11.25μm位置。从图中可以发现，在楔形光纤中，大部分光场能量仍存在于纤芯中，包层中的能量则比较少。由图中两根曲线关系，可以判断出，光场能量向楔形光纤的楔边方向靠拢，在进入楔形光纤后，其下方包层中的能量要大于开始端的。

Fig.3 Energy distribution in z-x plane of single wedge-shaped micro/nano fiber

为了更直观地表明能量在楔形微纳光纤中的传输，图3中给出了楔形微纳光纤的能量分布图，可以看到，楔形微纳光纤前端对能量的束缚较好，越靠近尖端，能量被束缚在楔形光纤的表面越明显。因此，对于楔形光纤，受其楔形结构的影响，电场能量主要沿着楔边向尖角方向集中，但又不是一直集中下去，在某个位置之后会出现纤芯表面的能量要强于纤芯中的情况。随着楔形部分有效直径D的减小，光纤对能量的束缚能力是先增大后减小，所以楔形光纤中的能量密度先增大到最大值，之后就一直减少。

2.2 两根楔形微纳光纤的耦合特性

楔形微纳光纤的能量耦合结果如图4所示。图4a图是在光纤z-x截面上的能量分布，图4b图是在光纤z-x截面上z=0μm位置处的能量密度变化图。通过耦合区域，光场从左边光纤耦合进了右边光纤，但也伴随着能量的损耗。结合图4a和图4b可以看到，在楔形区域的尖端部分，即在传播方向x=10μm左右处，能量密度达到最大值，之后，左边光纤通过楔边向右边光纤耦合进能量，在两楔边之间的空气层有能量损失，所以右边光纤的能量密度要低于左边。在图4b中，x在10μm～12μm这个区域，能量密度有明显的下降，这是由于左边光纤的楔端将能量导向下方，在两光纤的轴线上，能量会明显地减少，随后，能量从左边的楔端部分耦合到了右边楔端，能量回到轴线上，所以能量密度有一定的增加。

Fig.4 Energy distribution of two wedge-shaped micro/nano fibers coupling

光纤中的耦合效率直接反应楔形微纳光纤耦合时的能量损失情况。对耦合效率定义为右边光纤出射光场的功率Poutput和左边光纤入射光场的功率Pinput的比值。对于楔形光纤的耦合，由于耦合间隙的存在，在楔形光纤的端面会出现菲涅耳反射对耦合效率的影响。关于菲涅耳反射对耦合效率的影响，本文中主要从反射系数与透射系数［16］而计算出。耦合效率的值在0～1之间，越大表明耦合效果越好，能量损失越少。

首先，研究两根楔形微纳光纤之间轴向位移a对耦合效率的影响。在楔形微纳光纤的楔角β=46.8°，径向位移r=0μm时，轴向位移a的变化对耦合效率的影响如图5a所示，方点连接的实线1为不考虑菲涅耳反射影响下的耦合效率，三角点连接的虚线2为考虑耦合效率下的耦合效率变化曲线 (下面类似，不再叙述)，可以看到考虑菲涅耳反射后，其耦合效率略低于不考虑下的情况。当轴向位移a处于0μm～2μm时，轴向位移a增大，耦合效率η减小得非常快;轴向位移a在2μm～3.8μm时，耦合效率η减小得相对较缓慢。当a增大到一定值时，楔角的能量基本都已经被损失，耦合到右边光纤的能量是左边光纤轴线左右的能量在间隙中向前传播耦合进的，所以随着a的增大，相对损失量较小，所以耦合效率η减小相对较缓慢。

Fig.5 Impact of axial displacement and radial displacement on coupling efficiency

接着，研究两根楔形微纳光纤之间的径向位移r对耦合效率的影响。在楔角β=46.8°，轴向位移a=0.5μm时，改变两根楔形微纳光纤之间的径向位移r，对耦合效率的影响如图5b所示。可以看到，径向位移从0μm增大到0.6μm，耦合效率η迅速地减小到了10%，继续增大径向位移r，耦合效率η逐渐趋于0。左边光纤圆柱形中的能量传输到靠近尖端区域时，能量束缚在轴线的下方，当产生径向位移时，第2根楔形光纤尖端部分区域很少能接收能量，能量在空气中被损失掉，径向位移r越大，没有光纤接收能量的区域越多，则损耗越多，导致了径向位移r的增大，耦合效率η减小比较快。在径向位移r＞0.6μm后，两根楔形微纳光纤基本已经错开，所以耦合效率η逐渐趋于0。

在光纤直径不变时，改变楔角，楔形光纤的长度随之发生变化，其直接影响楔形光纤耦合的模型结构。在径向位移r=0μm、轴向位移a=0.5μm 时，改变两根楔形微纳光纤的楔角β，耦合效率的影响如图6所示。可以看到，楔角β从0°增加到90°时，耦合效率先减小后增大。楔角β从1°增加到7°时，耦合效率相当大，此时楔形光纤的长度非常大，两根楔形微纳光纤的耦合区域都相当长，两根光纤的耦合区的接触面积特别大，所以能量损失特别小。楔角β从7°增加到50°，在此楔角范围下，楔形光纤的长度减小的非常快，两根光纤耦合区的接触面积逐渐减小，导致能量损失越来越多，所以耦合效率迅速的减小。随着楔角β的继续增大，耦合效率却越来越高，β从50°增大到85°，η从63%增加到了90%左右，其原因是楔角β越大，楔形光纤的长度变得特别短，聚集在光纤楔角的能量越向轴线附近靠近，在楔角顶端方向损失的能量越少，所以耦合效率越来越高。

Fig.6 Impact of wedge angle on coupling efficiency

3 结论

应用COMSOL Multiphysics仿真软件模拟研究了楔形微纳光纤的能量分布，并对两根楔形微纳光纤的耦合特性和耦合效率进行了数值分析。在楔形微纳光纤中，能量的分布为沿着楔边向尖端方向集中，但在某一位置时，会出现纤芯表面的能量密度要强于纤芯中的能量密度，之后随着传输距离的增大，纤芯中的能量损失越来越多，越靠近尖端，束缚在纤芯表面的能量越来越强。楔形微纳光纤发生耦合时，轴向位移、径向位移和楔角对耦合效率都有着较大的影响。轴向位移的增大和径向位移的增大，都会使得耦合效率先迅速减小，后缓慢减小，而楔角的增大，会使得耦合效率先减小，在大于50°后，耦合效率又逐渐增大。楔形微纳光纤可以用来设计一些光学器件如滤波器，也可以应用于光纤传感器等光电器件中，对楔形微纳光纤特性的理论研究可为其实际应用提供帮助。

［1］ CLOHESSY A M，HEALY N，MURPHY D F.Short low-loss nanowire tapers on single-mode fibers［J］.Electronics Letters，2005，41(17):954-955.

［2］ LI M，JING Y L，ZHI Zh Y，et al.Self-modulated taper drawing of silica nanowires［J］.Nanotechnology，2005，16(9):1445-1448.

［3］ FALCO A D，MASSARI M，SCULLION M G，et al.Propagation losses of slotted photonic crystal waveguids［J］.IEEE Photonic，2012，4(5):1536-1541.

［4］ CUI N D，LIANG J Q，LIANG Zh Zh，et al.Photonic crystals and 2-D photonic crystal waveguides［J］.OME Information，2009，26(10):19-27(in Chinese).

［5］ WEI J，JUN D，HONG W，et al.Design and fabrication of high-efficiency photonic crystal power beam splitters［J］.Optics Letters，2011，36(20):4077-4079.

［6］ RAHIMI S，HOSSEINI A，XU X，et al.Group-index independent coupling to band engineered SOI photonic crystal waveguide with large slow-down factor［J］.Optics Express，2011，19(22):21832-21841.

［7］ LIU Y G，CHE F L，JIA Zh A，et al.Investigation on the characteristics of micro/nano fiber Bragg grating for refractive index sensing［J］.Acta Physica Sinica，2013，62(10):250-255(in Chinese).

［8］ CI J Sh，CHENG D G，YI N，et al.Micro-structure analysis in the coupling region of fiber coupler with a novel electrical micro-heater［J］.Optical Fiber Technology，2011，17(6):541-545.

［9］ BERES C，de NAZARE F V B，de SOUZA N Ch，et al.Tapered plastic optical fiber-based biosensor-tests and application［J］.Biosensors and Bioelectronics，2011，30(1):328-332.

［10］ CASAS-BEDOYA A，HUSKO C，MONAT C，et al.Slow light dispersion engineering of photonic crystal waveguides using selective microfluidic infiltration［J］.Optics Lettters，2012，37(20):4215-4217.

［11］ XIONG Y，ZHU D Q，DUAN Ch F，et al.Small-volume fiber-optic evanescent-wave absorption sensor for nitrite determination［J］.Analytical and Bioanalytical Chemistry，2010，396(12):943-948.

［12］ HONG Z H，LI X W，ZHOU L J，et al.Coupling characteristics between two conical micro/nano fibers:simulation and experiment［J］.Optics Express，2011，19(5):3854-3861.

［13］ JUNG Y M，BRAMBILLA G，RICHARDSON D J.Broadband singlemode operation of standard optical fibers by using a sub-wavelength optical wire filter［J］.Optics Express，2008，16(19):14661-14667.

［14］ LI M T，SUMETSKY M.Subwavelength and nanometer diameter optical fibers［M］.Hangzhou:Zhejiang University Press，2009:44-60.

［15］ CAO Zh Q.Guided wave optical［M］.Beijing:Science Press，2007:4-5(in Chinese).

［16］ LIU Q N.Transmission formula and analysis of TM wave in 1-D photonic crystal［J］.Laser Technology，2014，38(3):325-329(in Chinese).