光纤激光阵列相干合束的研究

李 彪，刘 雁*，曾曙光，周 军，李 晶，冯笙琴，常雪荣

(1.三峡大学理学院，宜昌443002;2.中国科学院上海光学精密机械研究所，上海201800)

引 言

现代许多领域，如高能激光系统、空间光通讯、激光雷达和光电对抗等诸多领域，都需要高光束质量的激光器［1－3］。单一激光器受增益饱和、热效应、光学元件破坏等因素的影响都存在着输出功率的极限，所以多光束相干合束被认为是一个获得高功率、高亮度、和高光束质量的有效手段［4－7］。本文中分析了几种光纤激光阵列结构、相位差以及振幅随机抖动、光纤间距、传输距离等因素对相干合成的影响，最后用桶中功率［8］对相干合成光束质量进行了评价。

1 数学模型的建立

沿z轴方向传播的基模高斯光束的场，不管它是由何种结构的稳定腔所产生的，均可表示为如下一般形式［9］:

式中，c为常数因子，f称为高斯光束的共焦参量;R(z)为与传播轴线相交于z点的高斯光束等相位面的曲率半径;w(z)是与传播轴线相交于z点的高斯光束等相位面上的光斑半径，k为波数，r为任意一点与原点之间的距离。根据波的叠加原理，多列波同时存在时，在它们的交叠区域内每点的振动是各列波单独在该点产生的振动的合成，而对于非相干叠加情况下的光强，则为各光束光强的简单相加。模拟计算中光束波长为1064nm，光束束腰半径为1mm。

2 不同的光纤激光阵列结构对相干合成的影响

图1a～图1d中分别给出了6根、7根、18根、19根光纤组成的光纤激光阵列的结构图。每根光纤的半径为0.5mm，每个环的间隔为1.5mm。图2a～图2d中分别给出了这些光纤阵列在传输距离为5m的光强分布。

Fig.1 Four kinds of fiber laser array structure

图3中分别是这些光纤阵列在传输距离为50m的光强分布特点。这种强度分布和多光纤阵列相干和束远场的实验结果类似［10］。当传输距离达到50m时，高斯光束发散得很厉害，上面4种结构输出的光束在该位置处相干合成后的光强均呈现高斯分布，此时的光斑半径很大，光纤的数目越多在50m处相干合成后的光斑半径越小。

Fig.2 Optical intensity distribution of four kinds structure when z=5m

图4中分别给出了上面4种结构轴上点光强随传输距离变化的关系。图4a中给出了6根光纤结构轴上点光强随传输距离变化的关系，可以看到，在0m到9m时轴上点光强随传输距离的增加而增加，在9m之后轴上点光强随传输距离的增加而衰减，但是对比图4b中给出的7根光纤结构轴上点光强与传输距离变化的关系，发现图像的特点发生了很大的改变，在传输距离较近时，6根光纤结构是轴上点光强随传输距离的增加而增加，而7根光纤结构是轴上点光强随传输距离的增加而衰减，且7根光纤结构在传输距离为2m时出现光强的极小值，当传输距离达到9m，之后轴上点光强随传输距离的增加而表现出相似的衰减特性，由此可知，在去掉中心部分的1根光纤时改变近场的光强分布特性而不改变远场的光强分布特性，通过对比图4c和图4d，也可以得到这一结论。对比图4b和图4d发现，7根光纤结构的轴上点光强与传输距离变化的关系图像表现为先衰减后增加再衰减，当在7根光纤的基础上加一圆环组成图1d所示的19根光纤结构时，可以看到，轴上点光强先衰减再增加、又衰减再增加、最后衰减，即在有外加一层共两层的圆环的光纤结构下，轴上相比于单根光纤的光强多了两个极大值和两个极小值的点，这个结论也可以推广到根多层圆环的光纤结构上，即在单根光纤的基础上再加n层圆环组成的多层光纤激光器阵列，其轴上相比于单根光纤的光强多了n个极大值和n个极小值的点。这一结论同样可以通过对比图4a和图4c得到。

Fig.3 Optical intensity distribution of four kinds of structure when z=50m

Fig.4 Relationship between axial intensity and propagation distance

3 出射位相随机抖动对相干合成的影响

对于光纤激光器相干合成而言，只有每路光纤激光器的出射位相都相同或者相位差Δ=2π时，相干合束的光束质量最好。但是实际中，由于受到温度扰动、吸收不均匀性等随机因素的影响，每路光纤激光器输出的光束位相都是有随机误差的，这必将影响光束的光强分布，有必要仔细分析位相的随机变化对光束质量的影响。图5中分别给出了出射位相在0～π/2，0～π/4，0～π/6，0～π/10时的光强分布，可以看出，光强的最大值分别为 29.3987，37.8828，43.0241，49.0265。因此位相抖动越小相干合成光强峰值越高，光束能量越集中，光束质量越好。参考文献［11］中也反映出相位差对光纤激光和束的实验结果产生重要的影响。

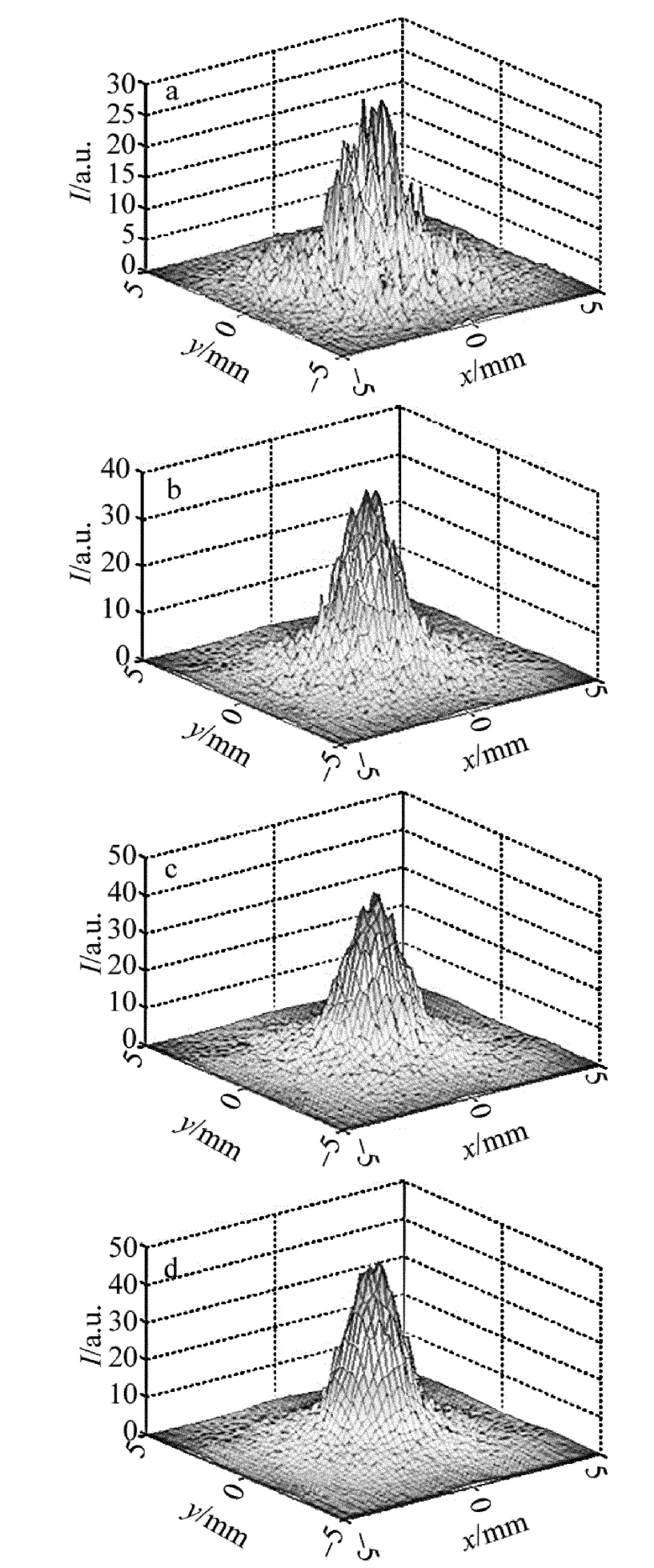
Fig.5 Effect of phase random jitter on coherent combination

4 光纤间距的变化对相干合成的影响

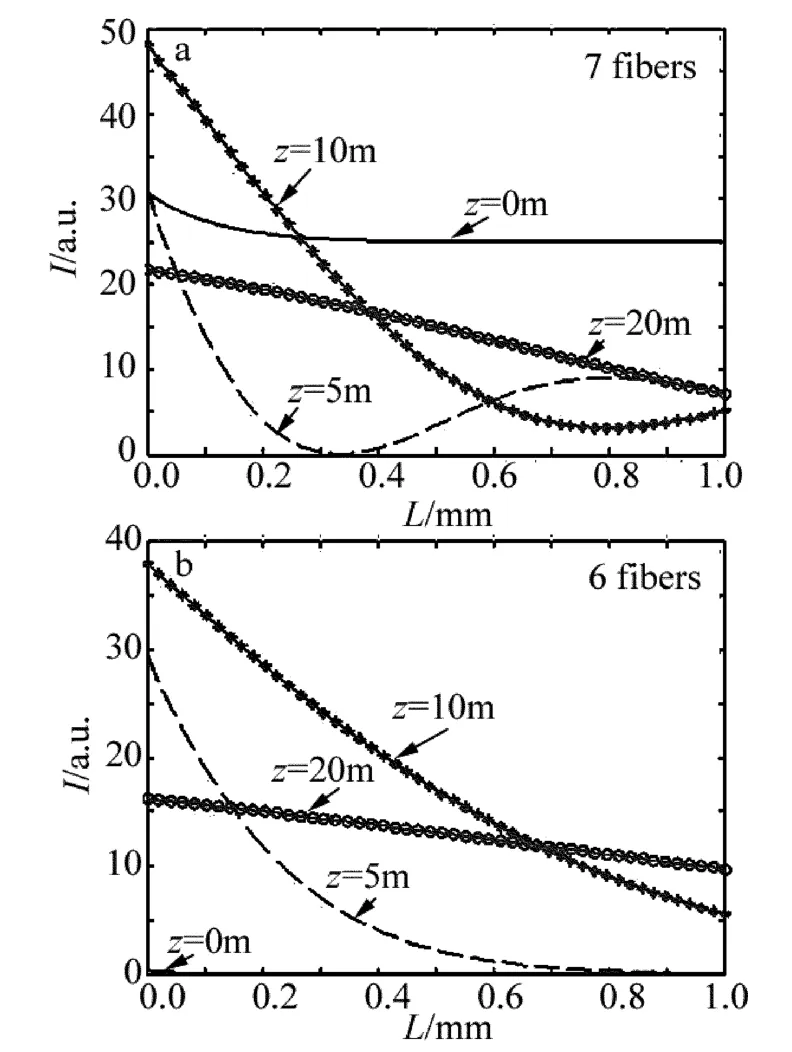
Fig.6 Relationship between axial intensity and fiber spacing

图6a中给出了7根光纤结构轴上点光强随光纤间距变化的关系，当光纤间距L在0mm到1mm之间变化时，不同的传输距离对应不同的关系，当传输距离为0m，光纤间距大于0.5mm时，光纤距离的增加对轴上点光强并无影响，此时传输距离为0m的轴上点的光强近似等于中心那根光纤输出的光强。当传输距离达到20m时，高斯光束已经发散，所以图像就表现为1条近似衰减的曲线，当传输距离为5m或为10m时，图像虽然总体上是衰减的，但是可以看出图像还是有起伏的，轴上点光强在随光纤间距变化的过程中，都出现了一个极小值，特别是当传输距离为5m时，在光纤间距为0.3mm左右的位置出现了光强为0的极小值点。图6b中给出了在采用上面的6根光纤结构时轴上点光强随光纤间距变化的关系，可以看出，不论传输距离如何，图像均为1条衰减的曲线，特别是传输距离为0m的时，轴上点的光强几乎为0，与光纤间距无关，因为去掉中间1根光纤后，其它6根光纤输出的高斯光束在轴上点的振幅十分微弱。当传输距离增加，由于高斯光束发散，在轴上部分的振幅才能加强。当光纤间距越大，由于高斯光束的发散，导致在轴上点的振幅也越微弱，表现为1条衰减的曲线。

图7中给出了6根光纤结构在不同传输距离时光斑半径随光纤间距变化的关系，可以看出，在传输距离远时光斑半径随光纤间距的增加而减小，但是减小的幅度不是很大，在传输距离近时光斑半径随光纤间距的增加而增加。

Fig.7 Relationship of the spot radius and fiber spacing of 6 fiber lasers array

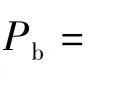
Fig.8 Relationship between power in the bucket and propagation distance

5 小结

对光纤激光阵列结构、相位随机抖动、光纤间距、传输距离等这些在实际中对光纤激光阵列相干合成有重要影响的因素做了数值分析，对实际中的光纤激光阵列相干合成有重要的指导作用，比如在实际中由于受到温度扰动、吸收不均匀性等因素的影响，必须考虑相位随机抖动对相干合成的影响。

［1］ HE B，LOU Q H，ZHOU J，et al.Coherent beam combination of fiber lasers［J］.Laser ＆ Optoelectronics Progress，2006，43(9):47－54(in Chinese).

［2］ ZHAO Sh，FAN W D，SHENG Q Q.The research of coherent combining of fiber laser［J］.Laser ＆ Infrared，2006，36(10):920－924(in Chinese).

［3］ MA Y X，SI L，ZHOU P，et al.The key technologies in coherent beam combination of high power fiber laser［J］.Journal of National U－niversity of Defense Technology，2012，34(1):38－43(in Chinese).

［4］ ZHOU J，HE B，XUE Y H，et al.Study on passive coherent beam combination technology of high power fiber laser arrays［J］.Acta Optica Sinica，2011，31(9):0900129(in Chinese).

［5］ WU B，LIU Y Zh.Coherent combination of high power fiber laser beams［J］.Laser ＆ Optoelectronics Progress，2006，43(8):56－61(in Chinese).

［6］ CHEN J，XUE H Zh，LIU X W，et al.Study of laser beam coherent combination［J］.Opto－Electronic Engineering，2011，38(9):65－70(in Chinese).

［7］ LI F D，GUO H N，SUN J G，et al.Simulation and experimental study on coherent combination of dual beam fiber laser［J］.Laser Technology，2014，38(7):509－514(in Chinese).

［8］ ZHAO N，TANG Ch，XIE G，et al.Numerical simulation on coherent combination of multi－beam super－Gaussian laser［J］.High Power Laser and Particle Beams，2007，19(11):1779－1782(in Chinese).

［9］ ZHOU B K，GAO Y Zh，CHEN T R.Principles of lasers［M］.5th ed.Beijing:National Defence of Industry Press，2004:70(in Chinese).

［10］ LI Zh，XUE Y H，ZHOU J，et al.Evaluation and measurement for beam quality of coherent beam combination of lasers in two－dimensional distribution［J］.Chinese Journal of Lasers，2011，38(4):0402002(in Chinese).

［11］ HOU J，XIAO R，JIANG Z F，et al.Coherent beam combination of three ytterbium fiber amplifiers［J］.High Power Laser and Particle Beams，2006，18(10):1585－1588(in Chinese).

［12］ LÜ B D.Laser optics:beam characterization，propagation and transformation，resonator technology and physics［M］.Beijing:Higher Education Press，2003:85(in Chinese).