基于岭回归—BP神经网络的管制工作负荷预测方法

温瑞英，王红勇

(中国民航大学 空中交通管理学院，天津300300)

基于岭回归—BP神经网络的管制工作负荷预测方法

温瑞英*，王红勇

(中国民航大学 空中交通管理学院，天津300300)

基于空中交通复杂程度刻画管制工作负荷是当前空中交通管理领域的研究热点.本文采集了厦门空管站的雷达数据，计算得出10个空中交通复杂性评价指标数值，通过共线性诊断发现复杂性指标间存在较强的多重共线性.在利用岭迹图对复杂性评价指标进行筛选的基础上，建立岭回归—BP神经网络组合模型对管制员工作负荷进行预测，并通过实测陆空通话数据进行验证.结果表明，本文提出的岭回归—BP神经网络组合模型收敛速度快、训练时间少；组合模型的均方误差、均方根误差、平均绝对误差、平均绝对相对误差等4项性能指标都相对较小，预测精度较高.

航空运输；管制员工作负荷；岭回归；神经网络；交通复杂性

1 引 言

随着空中交通流量的持续增加，管制员的工作负荷也随之增大.对管制员工作负荷的精确评价和预测是保障飞行安全、提升管制服务品质的基础.管制工作负荷评估方法主要有管制员生理及行为特征的测量、主观评价及交通复杂性测量等三个方面[1].Costa，Averty等通过测量管制员的生理和行为特征得出管制工作负荷强度[2，3]，该方法测量的几个关键指标在一定程度上能反映管制员工作负荷水平，但所需测量设备及环境要求较高，同时也可能对正常的管制工作带来负面影响，很难应用于实际管制工作.管制工作负荷的主观评价分为自我评估和专家评估[1].自我评估如美国联邦航空局的ATWIT技术，美国国家航空航天局的NSAS-TLX等[4]，这些方法需要通过编写调查问卷来评估管制工作负荷，由于管制员的个性差异，很难得到一种客观性评价结果；专家评价如国际民航组织通过规范性文件向各国推荐使用的DORATASK方法[5]，该方法将管制员的工作负荷划分为看得见的部分和看不见的部分，每部分的权值由专家打分确定，具有不确定性，同时看不见部分的工作任务不便进行记录和记时，所以专家评价法同样难以精确测量管制员的工作负荷.随着复杂性科学的发展，Mogford等提出了交通复杂性的概念[6]，通过研究不同管制指挥空域下交通特性的复杂程度来确定管制员的工作负荷水平，该方法可以更全面、客观地把握空中交通系统的运行规律，有助于精确地描述当前大流量、高密度交通环境下的管制工作强度.

本文基于实测雷达数据，计算得出10个空中交通复杂性评价指标数据，并进行了共线性诊断.为了提高管制工作负荷预测模型的精度，且去除指标数据间的多重共线性问题，分别基于岭回归、BP神经网络及岭回归—BP神经网络组合模型对管制员工作负荷进行预测，并对预测精度进行对比，以寻求一种有效的管制员工作负荷预测方法.

2 数据来源与指标的选取

2.1 数据来源

以厦门空管站02号管制扇区为研究对象，通过自主研发的数据处理软件对2013年9–10月期间每天08:00–21:00的雷达航迹数据、陆空通话数据进行解析处理.其中雷达航迹数据更新频率约4 s，内容包括航班经纬度、高度、航向、飞行速度等航班动态信息，将一段时间内的航班动态信息进行统计计算，可以得出该时段的交通流量信息，以及航班在该时段内的速度改变量、高度改变量、航向改变量等航班调整信息；陆空通话数据为管制员和飞行员通话音频文件，对音频文件进行解析后可获得每次陆空通话的通话时刻和相应的通话时长.本文以15 min为1个时间片，每个时间片内的计算结果为1个样本，有效样本数共计2 380个，其中2 219个样本用于岭回归建模和神经网络训练，161个样本用于验证分析.

2.2 空中交通复杂性评价指标

如果某一交通因素发生变化时，会影响特定交通状态的处理难度、交通混乱程度或者管制过程的灵活程度等，则该因素可作为空中交通复杂性的评价指标.基于厦门空管站的雷达数据，通过相关计算得出10个空中交通复杂性评价指标数据，所选指标如表1所示.

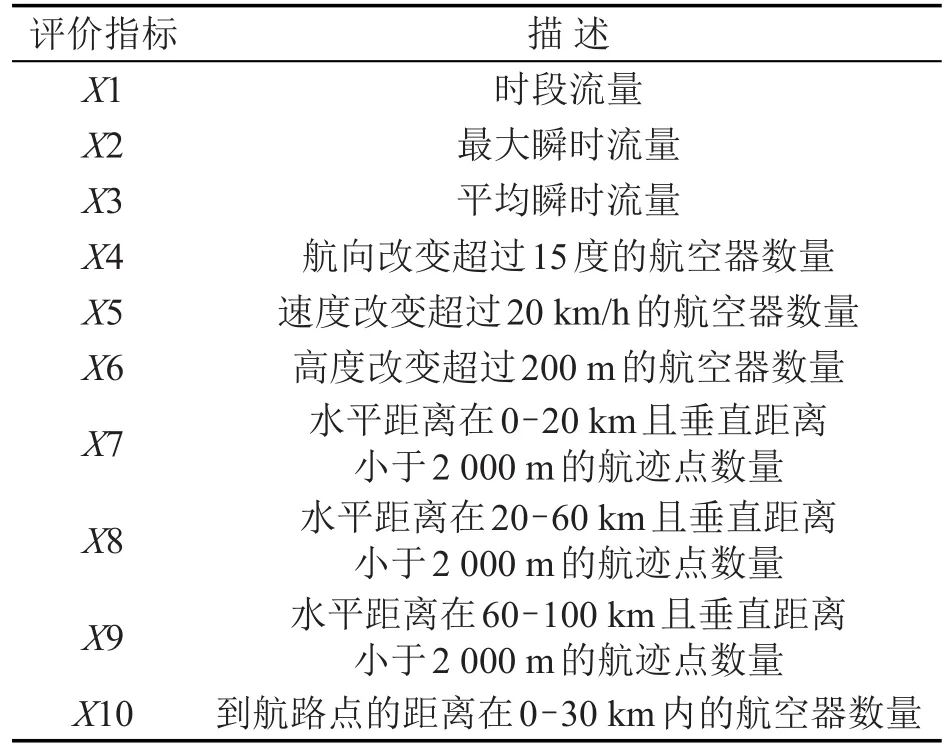
表1 空中交通复杂性评价指标Table 1 Air traffic complexity evaluation factors

2.3 管制工作负荷评价指标

语音通信是当前空中交通管制指挥的基本手段，管制员的整体工作负荷主要体现为通话负荷.本文以管制员的实际通话时长作为管制工作负荷的评价指标.

3 研究方法与原理

3.1 岭回归

岭回归方法主要用于处理自变量间的多重共线性问题.对于多元线性回归模型Y=Xβ+ε，Y为n×1观测向量，X=[x1,x2,…,xn]T为n×q列满秩矩阵，β=[β1,β2,…,βq]T为q×1未知参数向量.采用最小二乘法，向量β的估计值可由式（1）求解,的均方误差由式（2）计算，其中λi为非负对称矩阵XTX的q个特征根.

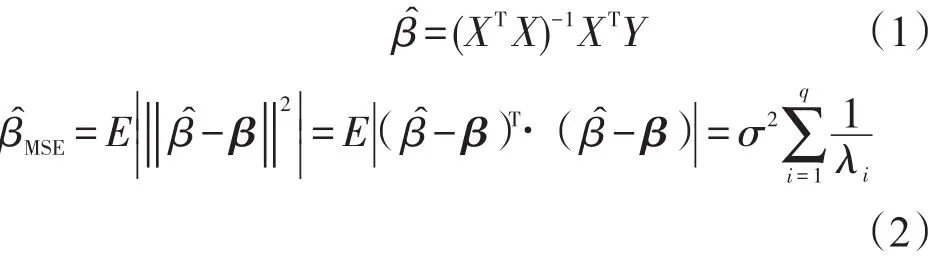
当自变量向量线性相关时，XTX奇异，它的一些特征根接近于零，的值会很大，说明估计值与观察值之间存在较大偏差，传统的最小二乘法失去稳定性与可靠性.如果采用 XTX+kI代替XTX，会使得矩阵XTX+kI的特征根远离零，的值减小，此时β的估计值可由式（3）求解.

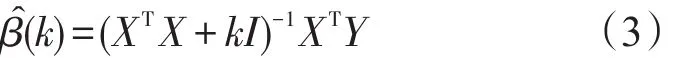
用岭回归法解决多重共线性问题的关键在于确定岭参数k，常用的方法有岭迹法、公式法、GCV法和L曲线法等[7].本文采用岭迹法来确定岭参数k，即在式（3）中，当k在[0,∞）之间变化时，的分量是岭参数k的函数，将t条函数曲线画出的图形称为岭迹，选取使的岭迹都大体稳定的那个点对应的k值作为岭参数.通过岭迹图，可以对影响管制员通话负荷的自变量因素进行筛选.本文利用岭迹筛选自变量的原则为：

(1)去掉岭回归系数比较稳定且绝对值比较小的自变量；

(2)去掉岭回归系数不稳定但随岭参数k的增加迅速趋于零的自变量[8].

为了消除评价指标间量纲不一致造成的影响，在进行岭回归分析时，采用Z-score标准化方法对原始数据进行处理，计算公式如式（4）、式（5）所示.

式中 Xi为第i个复杂性评价指标的原始数据，Y为通话时长的原始数据；为均值；SXi，SY为标准差；ZXi，ZY为标准化后的数据.

3.2 岭回归—BP神经网络模型

BP神经网络是基于误差反向传播算法、由非线性变化单元组成的多层前馈神经网络.其信息处理过程由神经元、激活函数、网络拓扑结构、连接权值和神经阈值所决定.BP神经网络学习算法的实质是通过误差反向传输不断调整权值和阈值使网络的误差平方和最小[9].图1为神经网络神经元的结构模型，x1，x2，…，xn为神经元的输入量，y为神经元的输出量或下一层神经元的输入，w1，w2，…，wn为权值，b为阈值，f为传递函数，.

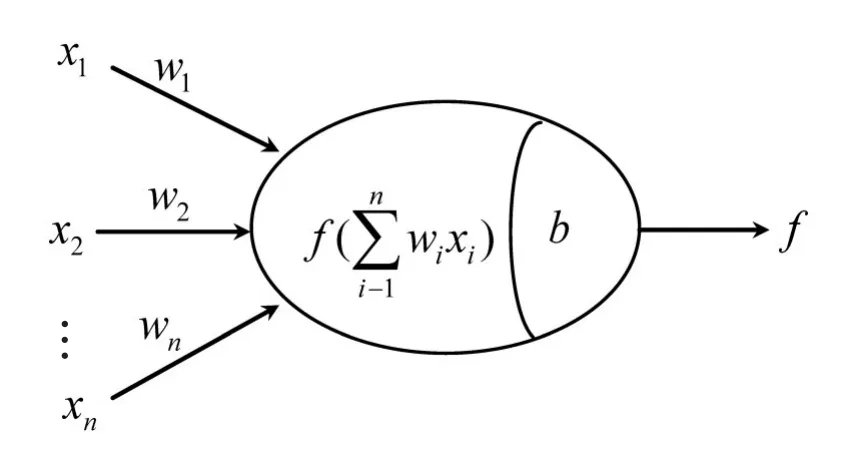
图1 神经网络神经元结构模型Fig.1 Neuronal structure model

本文采用MATLAB神经网络工具箱实现BP神经网络和岭回归—BP神经网络的设计、训练及测试.具体计算步骤为：

（1）数据归一化.

进行神经网络预测时，利用式（6）对数据进行归一化处理.

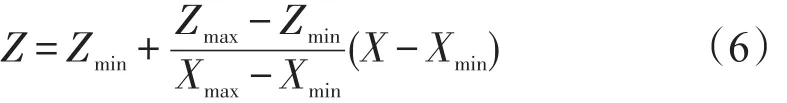
式中 X为原始数据；Xmax、Xmin分别为原始数据的最大值和最小值；Z为归一化后的数据；Zmax、Zmin分别为归一目标数据的最大值和最小值，取值为1和-1.

（2）岭回归—BP神经网络的构建.

BP神经网络的拓扑结构包括输入层、隐含层和输出层.Hecht证明一个3层的BP神经网络能够对任意非线性函数进行逼近[10]，因此本文采用3层网络结构，即输入层、隐含层和输出层各一个.神经网络模型没有对主导预测因子进行筛选的功能[11]，为了获得高效、精确的预测结果，在构建人工神经网络模型过程中输入变量的设置有2种，即全部自变量和岭回归筛选出的自变量；输出层为管制通话时长；隐含层节点数取决于输入层和输出层神经元个数及训练样本中所蕴含规律的复杂程度，本文在参照式（7）的基础上，通过试凑法来确定最佳隐含层节点数.

式中 m为隐含层的节点个数；l为输入层的神经元个数；n为输出层的节点个数；a为1–10之间的常数.

（3）网络的训练.

输入层与隐含层之间的传递函数采用正切S型函数（TANSIG），隐含层与输出层之间的传递函数采用纯线性函数（PURELIN）.为了减少迭代次数，提高收敛精度，训练函数采用附加动量因子自适应学习速率梯度下降算法（TRAINGDX），附加动量因子设为0.9，学习速率初始值设为0.01.反向传播权/阈值学习函数采用LEARNGDM，性能函数采用MSE.

4 结果与分析

4.1 共线性诊断

采用最小二乘法初步作多元线性回归，并进行多重共线性诊断，结果如表2所示.可以看出，回归模型各系数的显著性检验未通过，可初步判定回归方程存在多重共线性.X 3、X 10的容忍度≤0.1，方差膨胀因子≥10，说明这两解释变量与其余解释变量之间存在严重的多重共线性.其他指标的容忍度也较小，说明存在中等强度的多重共线性.

相关系数矩阵特征值如表3所示，可以看出，数据未标准化时的最大特征值为10.527，远大于其它特征值，有3个特征值接近于零，条件数为2 632＞1 000,说明变量间存在严重的多重共线性.数据标准化后的最大特征值为7.178，条件数为144＞100,说明变量间存在较强的多重共线性.

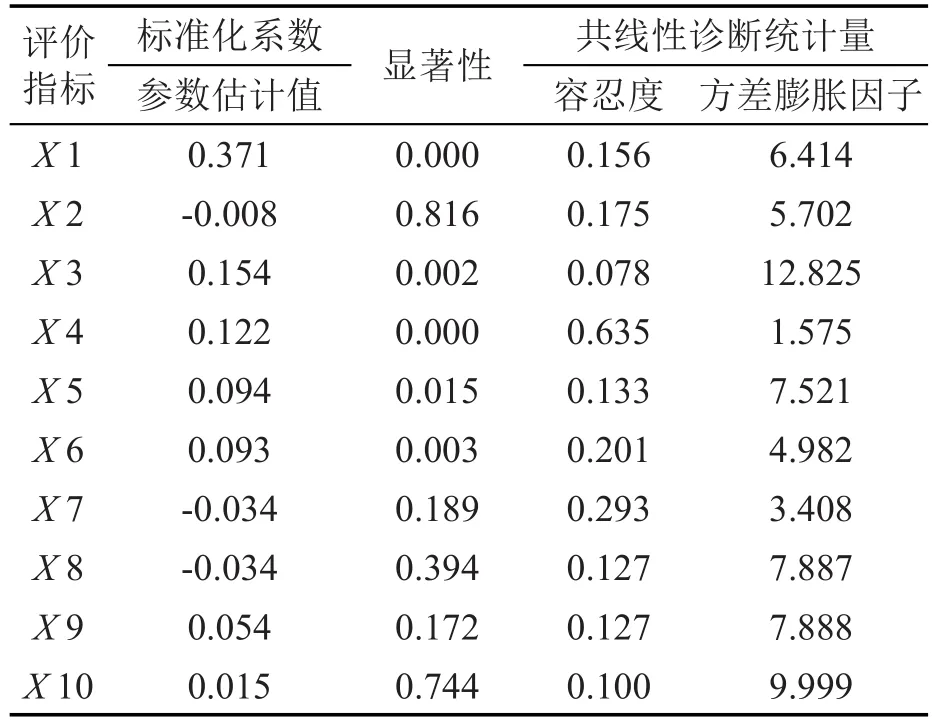
表2 回归参数估计及多重共线性诊断Table 2 Coefficients and co-linearity diagnostics

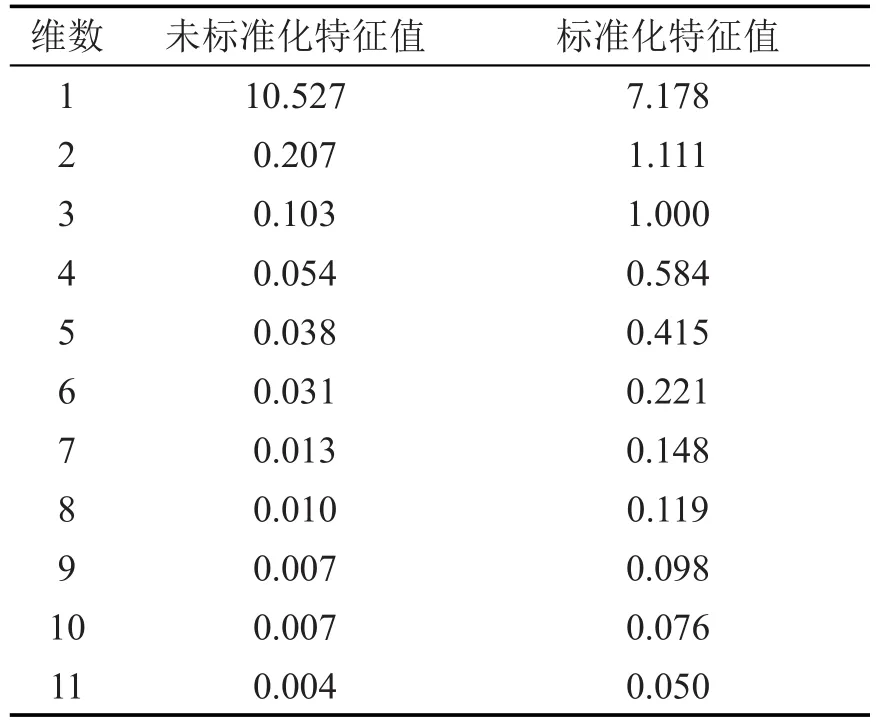
表3 相关系数矩阵的特征根Table 3 Eigenvalues of the correlation matrix

4.2 岭回归预测

由于自变量间存在多重共线性，故选用岭回归对管制员工作负荷进行预测.10个标准化自变量的岭迹图如图2所示.根据自变量筛选的第一条原则，ZX 7的岭回归系数稳定且绝对值比较小，这些变量应该去掉；根据自变量筛选的第二条原则，ZX 8、ZX 9的岭回归系数随岭参数K的增加迅速趋于零，这些变量也应该去掉；ZX 5、ZX 6的岭回归系数基本一致，说明这两变量对管制通话负荷的影响规律相同，可以保留一个变量，本文选取ZX 5来进行岭回归分析.

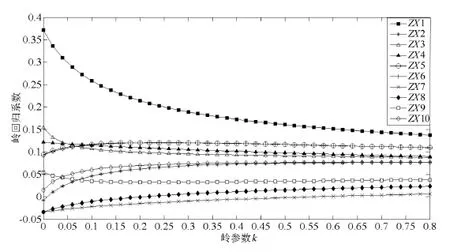
图2 10个标准化自变量的岭迹图Fig.2 The ridge trace plot of 10 standardized variables

图3为所选取的6个标准化自变量的岭迹图，可以看出当岭参数K＞0.25以后，各解释变量的回归系数基本趋于平稳（以水平直线为渐进线），故取岭参数为0.25时进行岭回归分析.

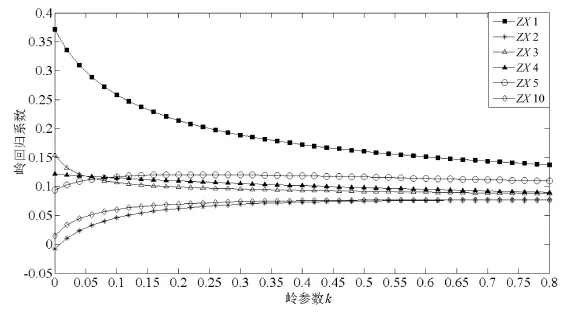
图3 6个标准化自变量的岭迹图Fig.3 The ridge trace plot of 6 standardized variables

根据岭回归原理，计算得出基于原始自变量的管制工作负荷预测模型如式（8）所示.可以看出，6个解释变量与管制通话时长均呈正相关关系.变量X 1的回归系数最大，说明时段流量对管制通话时长影响最大，时段流量越大，通话时长越长，管制工作负荷越高.其次为X 3，即平均瞬时流量，再次为X 5和X 4，说明速度改变和航向改变会增加空中交通的复杂程度，增大管制员的通话时长，增加管制工作负荷.

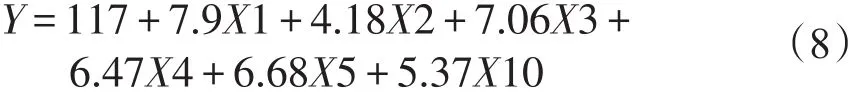
用未参加建模的161个样本数据对岭回归预测模型进行检验，管制通话时长的预测值和实测值如图4所示，可以看出预测数据与实测数据整体变化趋势相同，但在局部地方尤其是极值点处预测效果不理想.

图4 岭归回预测的管制通话时长Fig.4 The communication time by ridge regression

4.3 神经网络预测

选取归一化后的全部自变量和岭回归筛选出的自变量进行神经网络预测.BP神经网络和岭回归—BP神经网络的输入层神经元个数分别为10和6；输出层神经元个数均为1；根据式（7），针对可能的隐含层节点数，进行网络训练及测试，最终得出当隐含层节点数为4时，BP神经网络的训练误差与测试误差均达到较小水平，训练误差为0.068 14，测试误差为（未归一化）0.646 3；当隐含层节点数为6时，岭回归—BP神经网络组合模型的训练误差与测试误差均达到较小水平，训练误差为0.065 36，测试误差为（未归一化）0.615 7，因此确立BP神经网络和岭回归—BP神经网络的拓扑结构分别为10-4-1和6-6-1型.当使用最佳网络结构进行训练时，BP神经网络经过91次迭代后收敛，网络训练时间为6s；岭回归—BP神经网络经过83次迭代后收敛，网络训练时间为5 s.综上可得，岭回归—BP神经网络的收敛速度、稳定性及预测精度都比BP神经网络好.图5给出了161个测试样本数据的实测值和预测值散点图，对比图4可以看出所选的两种神经网络模型对管制通话时长的拟合精度均高于岭回归模型.

图5 神经网络模型预测的管制通话时长Fig.5 The communication time by neural network model

4.4 模型精度评价

为了克服单一误差指标对模型精度评价不科学、不可靠的缺点，选用均方误差（MSE）、均方根误差（RMSE）、平均绝对误差（MAE）、平均绝对相对误差（MAPE）等4项性能指标对预测模型精度进行评价[11]，如式（9）–式（12）所示.

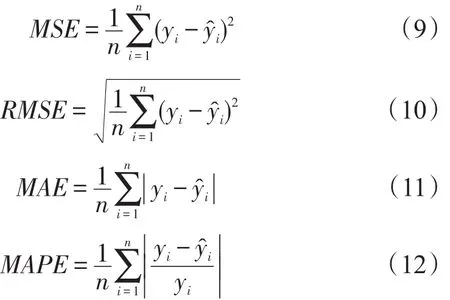
三种模型的各性能指标如表4所示.可以看出，岭回归—BP神经网络的各个误差指标都相对较小，其次为BP神经网络，岭回归模型误差最大，说明神经网络的预测精度要高于岭回归模型；岭回归—BP神经网络组合模型较BP神经网络的精度高，且具有较高的稳定性.

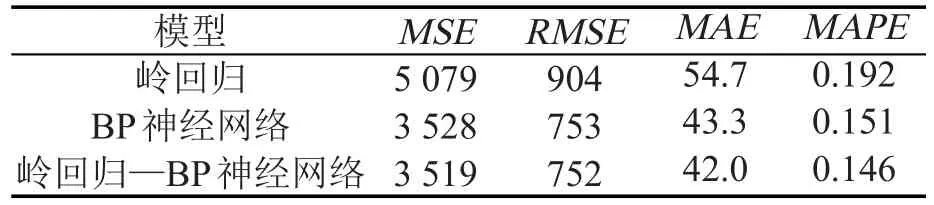
表4 三种模型预测性能对比Table 4 The perform ance com parison of three kinds of models

5 研究结论

采用厦门空管站的实测雷达数据对10个典型空中交通复杂性评价指标进行了计算，共线性诊断结果发现这些复杂性指标间存在较强的多重共线性.基于岭回归、BP神经网络和岭回归—BP神经网络构建了管制员工作负荷预测模型，并利用实测陆空通话数据进行了验证.数据统计结果表明，时段流量和平均瞬时流量对管制工作负荷影响最大，流量越大，管制工作负荷越高.飞机速度和航向的改变也会显著增加空中交通复杂程度、增大管制员的通话时长.本文提出的岭回归—BP神经网络组合模型相比岭回归模型预测精度较高，相比BP神经网络模型收敛速度、预测精度及稳定性都较好.

[1]张明,韩松臣,裴成功.空中交通管制员工作负荷研 究 综 述 [J].人类工效学,2008,14(4):61-64. [ZHANG M,HAN S C,PEI C G.Review of ATC controller workload[J].Chinese Journal of Ergonomics, 2008,14(4):61-64.]

[2]Costa G.Evaluation of workload in air traffic controllers[J].Ergonomics,1993,36(2):1111-1120.

[3]Averty P,Collet C,Dittmar A,et al.Mental workload in air traffic control:an index constructed from field tests[J].Aviation,Space and Environmental Medicine, 2004,75(2):333-341.

[4]Collet C,Averty P,Dittmar A.Autonomic nervous system and subjective ratings of strain in airtraffic control[J].Applied Ergonomics,2009,40(1):23-32.

[5]ICAO.Doc9426-AN/924(1st Edition)-1984.Air traffic service planning manual,partⅡ,Appendix C[S]. Montreal,Canada,ICAO,1999.

[6]Mogford R H,Murphy E D,Guttman J A.Using knowledge exploration tools to study airspace complexity in air traffic control[J].The International Journal of Aviation Psychology,1993,4(1):29-45.

[7]黄海兰,牛犇.岭参数确定的研究[J].测绘科学, 2011,36(4):31-32.[HUA H L,NIU B.Comparison of ridge parameter determination[J].Science of Surveying and Mapping,2011,36(4):31-32.]

[8]王强,胡海清.基于岭回归和人工神经网络估测森林可燃物负荷量[J].林业科学,2012,48(9):108-114. [WANG Q,HU H Q.Estimation of forest fuel load based with ridge regression and artificial neural networks[J]. Scientia Silvae Sinicae,2012,48(9):108-114.]

[9]刘静,李亮,关伟,等.基于神经网络的北京环路交通流短期预测研究[J].交通运输系统工程与信息,2005, 5(6):110-115.[LI U J,LI L,GUAN W,et al.Short-term prediction of traffic flow in Beijing ring road based on neural network[J].Journal of Transportation Systems Engineering and Information Technology,2005,5(6): 110-115.]

[10]Hecht N R.Kolmogorov’s mapping neural network existence theorem[C].Proceedings of the International Conference on Neural Networks,New York:IEEE Press, 1987.

[11]李蓬勃,闫晓冉,徐东瑞.BP神经网络和多元线性回归在粮食产量空间分布预测中的比较[J].干旱区资源与环境,2014,28(9):74-79.[LI P B,YAN X R,XU D R.Comparison of grain yield spatial distribution forecast between the models of BP neural network and multiple linear regression[J].Journal of Arid Land Resources and Environment,2014,28(9):74-79.]

A Forecasting Method of Controller’s Workload Based on Ridge Regression—BP Neural Network

WEN Rui-ying，WANG Hong-yong
（Air Traffic Management College,CivilAviation University of China,Tianjin 300300,China)

It is becoming a new hot topic in the field of air traffic management that evaluating the controller’s workload by the traffic complexity factors.Based on the radar data of Xiamen air traffic control station,10 typical complexity evaluation factors were calculated.The strong multi-co-linearity among various complexity factors is discovered through co-linearity diagnosis.Using the ridge trace plot of ridge regression,the complexity evaluation factors are selected,and the combined model of ridge regression and neural network are established to predict the controller’s workload.The forecasting results are verified by the pilot/controller voice communication data.It shows that the combination model of ridge regression and BP neural network has fast convergence speed and less training time.The combined forecasting model has high precision because four performance indexes such as mean square error,root mean square error,mean absolute error and mean absolute relative errors are relatively small.

air transportation;controller’s workload;ridge regression;neural network;traffic complexity

1009-6744（2015）01-0123-07

：V35

：A

2014-07-25

：2014-11-17录用日期：2014-12-08

国家自然科学基金委员会与中国民用航空局联合资助项目（U1333108）；天津市应用基础与前沿技术研究计划(14JCQNJC04500)；中央高校基本科研业务费(ZXH2011C007)；校级科研启动基金（08QD01X）.

温瑞英（1977-），女，山西忻州人，博士. ＊

：wenruiying@163.com