浙江省奶牛布鲁氏病的到达时间的研究
2015-04-19李峰
李峰
(山西农业大学 文理学院,山西 太谷 030801)
浙江省奶牛布鲁氏病的到达时间的研究
李峰
(山西农业大学 文理学院,山西 太谷 030801)
在我国,布鲁氏菌病被列为二类动物疫病。随着中国奶牛养殖的规模化经营,奶牛在城市间频繁调运,致使疫区广泛分布,所以研究疫病到达时间对疫病防控非常重要。本文以城市为斑块,建立了多斑块动力学模型,利用随机的方法给出疫病到达时间的一般表达式。以中国南方最大的奶牛基地——浙江省为例,结合实际调研的数据,验证了模型的合理性,并给出了杭州、宁波、金华、温州、台州、湖州、衢州这7个辖市的奶牛布病的到达时间,为布鲁氏菌病的防控提供了理论基础。
布鲁氏菌病;浙江;动力学模型;疫病到达时间;
布鲁氏菌病(Brucellosis,以下简称布病)是由布鲁氏菌引起的羊、牛、猪、犬以及人等均可发生的一种人畜共患的慢性传染病。世界动物卫生组织(OIE)将其列为B类动物疫病,我国将其列为二类动物疫病。动物布病以羊、牛和猪最易感,犬及60多种家畜、家禽、野生动物有不同程度的易感性,其特征主要是侵害生殖系统,引起流产、不孕、睾丸炎等。人布病,又称地中海弛张热、马尔他热、波浪热等,其特征为呈现波浪热、关节痛、睾丸炎等症状,染病的急性期可以治愈,但不易被认症,常被拖延为慢性期,未经治疗者的自然病程为3至6个月,短仅仅1个月或长达数年以上,严重影响人的身体健康[1]。
布病在中国流行已久,疫区分布广泛,经多年防治,在20世纪80年代中后期得到有效控制,布病疫情大幅下降,近年来,随着我国家畜饲养量不断增加,畜禽及其产品的流通日益频繁,畜间布病疫情在相当一部分省区又呈现了活跃态势,部分省份出现人间布病暴发点,说明畜间布病疫情相当严重[2]。根据《全国传染病疫情资料》对全国31个省市区近年来人间布病的统计表明,有28个省市区在人间有布病疫情报告(不包括只有畜间疫情报告省区)。目前,我国布病的传播主要与羊群的调运有关[3]。
浙江为我国南方最大的奶牛基地。浙江省下辖杭州、宁波、温州、绍兴、湖州、嘉兴、金华、衢州、舟山、台州、丽水11个市,2011年,对浙江奶牛进行了实地调研,得到了2001—2010年这11个辖市奶牛的扑杀数据。对奶牛的养殖情况进行了参观,大约95%的奶源分布在杭州、宁波、金华、台州和温州。杭州、宁波和金华的几家大的乳品公司所辖的养殖场采用统一经营、统一饲养的模式,金华奶牛养殖还采用养殖小区的模式,即集中饲养、分户经营,也有一部分是分户经营和饲养,其他几个市主要是分户经营和饲养,但在未来计划采用养殖小区的形式。由于养殖量的增加和养殖模式的不同,以及奶牛的补栏除了自繁以外,还有部分从外地调入,导致了各地的发病情况不同,而且随着国家和地方政策对奶牛业的大力扶持,使得养殖量增加,布病的发病数也相应增加[4]。分析研究调运对布病的影响,对制定防控措施非常重要,考虑调运就需要建立个体迁移的模型,个体的调运直接反应疫病到达该地的时间,即将无病地区的易感者第一次与染病者接触的时间。
有关迁移模型,主要有随机模型和斑块模型。Rvachev和Longini[5]构建了基于全球航空网络的流感模型。Wendi W和Xiaoqiang W[6],Jin Y和Wendi W[7]构建了个体在n个板块间迁移的模型。关于疾病到达时间,目前主要是基于航空网络,关注的是人类疾病的到达时间。Colizza等人[8,9]构建了基于全球航空网络的随机模型,通过对全球航空网数据的统计分析,预测各地疾病的流行规模和暴发时间。AurvelienGautreau等人[10]构建了SI集合种群模型,给出了疾病到达时间的一般表达式。
为研究布病在中国传播的内在机制,并最终提出有效的防控措施,根据以上分析,本文在将构建个体在斑块间迁移的动力学模型,在此基础上给出疫病到达时间的一般表达式,最后利用杭州、宁波、金华、温州、台州、湖州、衢州这7个辖市的奶牛布病的数据,验证模型的合理性,给出这7个辖市的奶牛布病到达时间,为防控措施的建立提供理论依据。
1 模型介绍

根据以上假设和机理分析,可以建立以下动力学模型:
假设初始时刻,即t=0时,第i个斑块为无病斑块,而其它斑块可能存在染病牛,当第i个斑块从其它斑块调入染病牛时,布病可能会在第i个斑块内传播,将第i个斑块内的易感牛与从其他斑块调入的染病牛的第一次接触的时间(即疫病到达时间)记作Ti,根据AurelienGautreau1,AlainBarrat等[10]提出的方法计算第i个斑块的疫病达到时间Ti。pij表示单位时间内第j个斑块的染病牛迁到第i个斑块的概率,pij=bijΔt。假设第i个斑块从第j个斑块调入染病牛的疫病到达时间tij=nΔt,即从t=0时刻开始,直到nΔt时刻,第i个斑块的易感牛才与从第j个斑块调入的染病牛第一次接触的概率:
文中的所有式子中的[]都表示对括号中的式子取整数。相对于第j个斑块的牛群总数而言,在单位时间内从第j个斑块调到第i个斑块的染病者数量非常的小,即
pij=bijΔt≪1,
则式(2)可以化简为:
当t 所以Ij(t)=Ij(0)eΛjt, 将上式代入式(3)得: 因此,从第j个斑块调入染病牛,造成第i个斑块的牛群感染的疫病到达时间tij的密度函数为: (4) 为使P(t)>0恒成立,式(4)中的Θ(t)为Heavisid函数。显然,疫病到达时间tij服从Gumbel分布,那么 其中γ为Euler常数。所以第i个斑块的疫病到达时间: (j≠i=1,2,…,7). 基于系统(1),将模型与实际数据进行拟合。首先分析实际数据得到以下重要参数的取值: ν=0.12,η=0.1。 拟合结果见图1。通过数值模拟得到以下主要参数的取值: λ1=0.19,λ2=0.2,λ3=0.2,λ4=0.4,λ5=0.4,λ6=0.03,λ7=0.3;β1=8.6×10(-4),β2=4.5×10(-4),β3=6.1×10(-4),β4=8.4×10(-4),β5=4.5×10(-4),β6=25.6×10(-4),β7=89.1×10(-4). 浙江省杭州、宁波、金华、温州、台州、湖州和衢州7个辖市布病的到达时间见图2. 图1 2001-2010年浙江省杭州、宁波、金华、温州、台州、湖州和衢州7个辖市奶牛布病扑杀数的实际数据与模型拟合结果的比较 图2 杭州、宁波、金华、温州、台州、湖州和衢州7个辖市的布病实际到达时间与模型得到的到达时间的比较 Fig.2 TheactualpositivetestingdataofthearrivaltimeofbrucellosisiscomparedwiththeoutcomesofmodelfittingofHangzhou,Ningbo,Jinhua,Wenzhou,Taizhou,HuzhouandQuzhou 本文构建了包括迁移的多斑块动力学模型,给出了疫病到达时间的计算方法和一般表达式,并通过实例验证了模型的合理性,计算出的疫病到达时间基本和实际数据相吻合。因此此方法可以应用到与迁移有关的动物疫病、人类疾病以及人蓄共患病的研究中,对传染病的防控措施的研究有很重要的意义。 [1]胡邵谦,黄志刚.布鲁氏菌病防控存在的主要问题及策略[J].中国初级卫生保健,2010,24(6):84. [2]张见麟.近期布鲁氏菌病发病率上升的原因及防控措施建议[J].疾病监测,2010,25:311-312. [3]李秋丽,夏蔚,张彤,等.人畜布鲁氏菌病流行特征的数据分析[J].数理医药学杂志,2008,21:621-622. [4]吴艳,权亚玮.奶牛场防控布鲁氏菌病存在的问题及净化措施[J].畜牧与饲料科学,2010,31:120-121. [5]Longini I M.A mathematical model for predicting the geographic spread of new infectious agents[J].Mathematical Biosciences,1988,90: 367-383. [6]Wendi Wang,Xiaogiang Zhao.An endemic model in a patchy environment[J].Math Biosci,2004,190:97-11. [7]Wendi W,Yu J.The effect of population dispersal on the spread of a disease [J].Math Anal Appl,2005,308:343-364. [8]V Colizza,A Barrat,M·Barthelemy.The role of the airline transportation network in the prediction and predictability of global epidemics[J].Proc Natl Acad Sci,2006,103: 2015-2020. [9]V Colizza,A Barrat,M·Barthelemy.The modeling of global epidemics:stochastic dynamics and predictability Bull [J].Math Biol,2006,68:1893-1921. [10]Aurvelien Gautreau,Alain Barrat.Global disease spread: statistics and estimation of arrival times[J].Journal of Theoretical Biology,2008,251: 509-522. (编辑:马荣博) The Arrival Time of Brucellosis In terms of Dairy Eow in Zhejiang Province Li Feng (CollegeofArtsandSciences,ShanxiAgriculturalUniversity,TaiguShanxi030801,China) In our country,brucellosis is listed as the second class animal epidemics.As China's dairy farming scale management,frequent dispatching between cows in the city,the area is widely distributde,so the arrival time is very important for disease prevention and control of disease.Taking cities as plates,more plates dynamical models were established.By using the method of random,the general expression of the arrival time of disease were given.In southern China,took the largest dairy cows bases,zhejiang province as an example and combined with the actual survey data,the rationality of the model was verified.And the arrival time of brucellosis was given in terms of dairy cow in Hangzhou,Ningbo,Jinhua,Wenzhou,Taizhou,Huzhou,Quzhou.This study provides the theory basis for prevention and control of brucellosis. Brucellosis;Zhejiang;Dynamical model;The arrival time of disease 2015-01-13 2015-03-20 李峰(1981-),女(汉),山西平遥人,助教,硕士,研究方向:应用数学。 O175 A 1671-8151(2015)03-0297-042 数值模拟
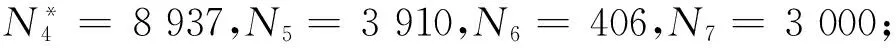

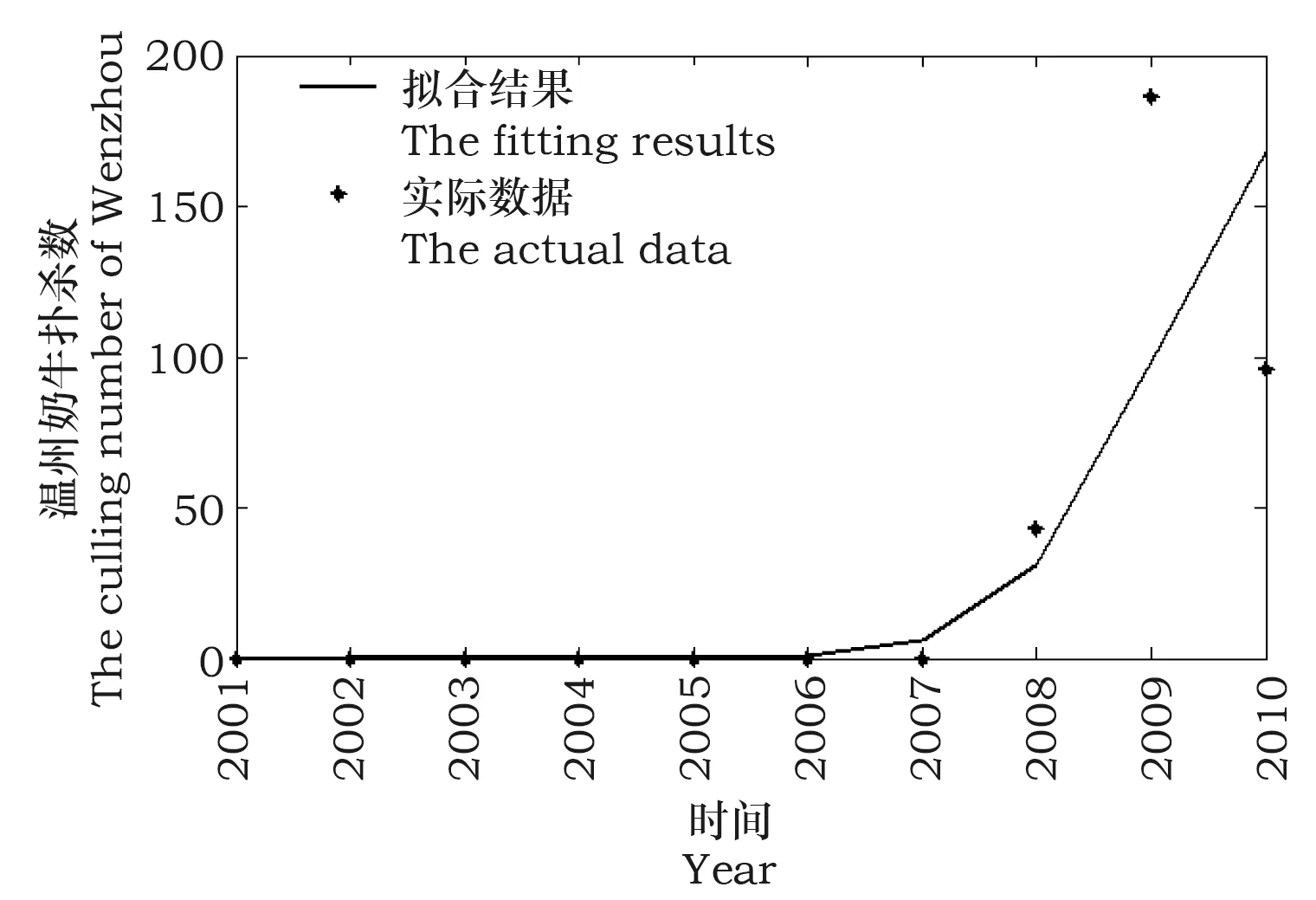

Fig.1 The actual positive testing data of culling number in terms of dairy cow is compared with the outcomes of model fitting of Hangzhou,Ningbo,Jinhua,Wenzhou,Taizhou,Huzhou and Quzhou3 结语
