双渠道供应链博弈模型的复杂性分析
2015-04-19张婷婷马小林
张 芳,张婷婷,马小林
(天津工业大学理学院,天津 300387)
双渠道供应链博弈模型的复杂性分析
张 芳,张婷婷,马小林
(天津工业大学理学院,天津 300387)
提出了由一个制造商和一个零售商组成的双渠道供应链博弈模型,研究了集中决策和分散决策2种决策下的静态和动态博弈模型,分析了静态模型下零售渠道的渠道忠诚度对定价决策的影响,并利用稳定域图、分岔图、最大Lyapunov指数图研究了动态模型的复杂动力学性质.研究结果表明:零售价与零售渠道忠诚度成正比,直销价与零售渠道忠诚度成反比;分散决策下的零售价格大于集中决策下零售价格;集中决策下,整体供应链能够获得更大的利润.
双渠道供应链;博弈模型;渠道忠诚度;定价;混沌
近20年来,随着电子商务的迅猛发展,消费者的消费方式发生了巨大的改变,网上购物的消费者越来越多.据不完全统计,2011年我国网络零售交易额已超过8 000亿元,占消费品零售总额的4%.根据纽约时报的调查,大约42%左右的工业产品供应商(如IBM,Pioneer Electronics,Cisco System,Estee Lauder,Nike)已经建立了直销渠道,通过互联网向顾客销售产品[1].在电子商务下生产商必须重新制定渠道选择与管理策略以应对网络经济带来的挑战[2-5].在渠道选择方面,Kumar等[6]研究了生产商试图在保留零售商渠道的同时增加一个直接渠道,结果表明生产商可以通过建立直接渠道获得更多的收益,而同时零售商也可能因此而受益.Hendershott和Zhang[7]发现:在传统零售商的基础上,增加直接渠道可以使制造商从零售商手中吸引高价值顾客而使利润增加,但零售商的处境却变得糟糕,销售量和利润均下降,渠道冲突在所难免.双渠道供应链的定价决策也是一个长期的动态博弈.Guo等[8]研究了一个制造商和一个零售商的闭环供应链定价决策的博弈模型,分析了分岔图,混沌和连续功率谱等动力学现象.Ma等[9]研究了一个制造商和一个零售商组成的闭环供应链(CLSC)的产品回收问题,分析了分岔图,最大Lyapunov指数(LLE),混沌和初始值的灵敏度等动力学现象.结果表明,随着零售商的竞争地位的提高,闭环供应链系统将更容易进入混沌.
本文在上述相关文献的研究基础之上,建立双渠道供应链博弈模型,研究集中决策和分散决策2种决策下的静态和动态博弈模型,分析消费者渠道忠诚度对定价的影响,通过分岔图和最大Lyapunov指数(LLE)分析该模型的动力学行为.
1 问题描述与模型
1.1 问题描述
本文中,考虑单一产品含有一个制造商、一个传统零售商和若干消费者的供应链.由于网络购物的迅速发展,制造商打算在传统零售渠道之外开设一个电子直销渠道.其模型如图1.

图1 供应链系统Fig.1 Supply chain systerm
图中:ω为单位批发价;pm为直销渠道的单位直销价格;pr为零售渠道的单位零售价格.
1.2 模型建立
在双渠道供应链中,假设对同一商品,商品的渠道价格和渠道忠诚度决定了渠道需求,本文借鉴文献[10-11]中的线性需求函数,制造商和零售商的需求函数描述如下:

式中:Dm、Dr为零售渠道和直销渠道的消费者需求函数.假设a为销售渠道(直销渠道和零售渠道)的潜在市场规模,θ为消费者对零售渠道和直销渠道的渠道忠诚度,其中0<θ<1,则ar=θa,am=(1-θ)a分别为零售渠道和直销渠道的潜在市场规模.b1、b2分别为Dr、Dm对自身价格和交叉价格的敏感性系数,b1>b2.由此,可以写出零售商的利润函数为:

制造商的利润函数为:

双渠道供应链的整体利润
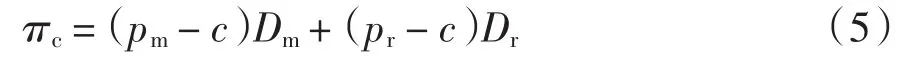
式中:c为单位生产成本.
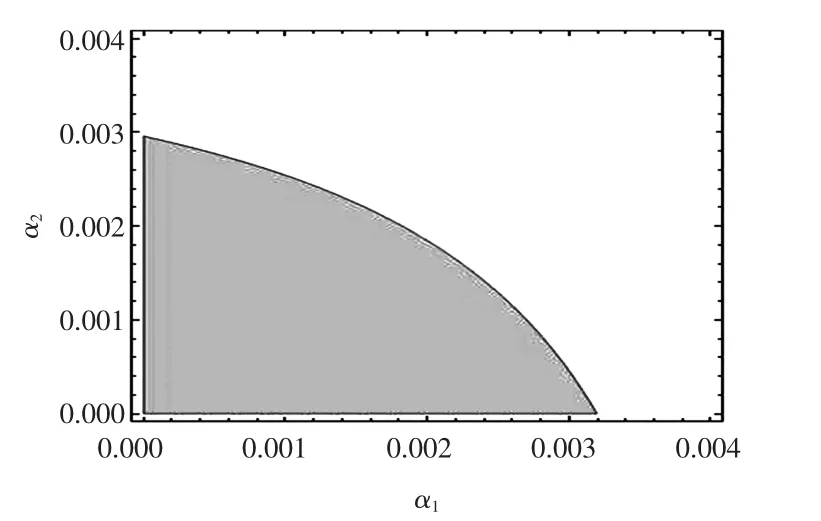
一般来说,参数应满足以下条件:①c<ω 在集中决策的双渠道供应链中,制造商与零售商共同决策,使供应链整体利润达到最优,决策变量为pm、pr. 2.1 静态模型与分析 2.1.1 静态模型 对供应链整体利润函数πc求关于pm、pr的二阶偏导,可得 式(9)即为集中决策下最优定价,把式(9)代入利润函数πc,得到最优整体利润 2.1.2 静态模型分析 命题一 零售价与零售渠道忠诚度成正比,直销价与零售渠道忠诚度成反比. 证明 根据以上结果分析零售渠道的渠道忠诚度θ对集中决策下价格的影响. 由以上一阶偏导结果可以看出零售价格与零售渠道忠诚度成正比,直销价格与零售渠道忠诚度成反比,也就是说,随着θ的增加,零售价增加,而直销价减少.在双渠道供应链中,分析集中决策下零售渠道的渠道忠诚度直销渠道价格、零售渠道价格和整体供应链利润的影响,取参数a=400,b1=5,b2=3,c=30,可得图2. 由图2可以看出,在集中决策模型下,零售渠道的渠道忠诚度θ与批发价pm成反比,与零售价pr成正比.当θ<0.5时,pm>pr,整体供应链利润呈下降趋势;当θ>0.5时,pm 2.2 动态模型与分析 2.2.1 动态模型 由于信息收集和决策者经验等方面的差异,在市场不完全信息条件下各节点企业掌握的信息也是不完全相同的,他们有着不同的理性水平.因此,制造商和零售商基于有限理性期望进行价格决策.在边际利润的基础上调整了博弈过程,如果在t期的边际利润是正的,那么在t+1期将输出其调整策略调整后的价格,即:p(t+1)=p(t)+α2p(t)则集中决策下模型调整策略如下: 图2 集中决策下零售渠道的渠道忠诚度θ对价格和利润的影响Fig.2 Influence of retail channel loyalty on price and profit under centralized decision 式中:α1为pm的调整系数;α2为pr的调整系数. 2.2.2 动态模型分析 系统(11) 有 4个均衡点:E0=(0,0),E1=,E*=其中, 系统(11)的Jacobian矩阵为: 式中:A=1+α1(am-4b1pm+2b2pr+(b1-b2)c);B=1+α2(ar-4b1pr+2b2pm+(b1-b2)c). 在E0处它的特征值为λ1=1+α1(am+(b1-b2)c),λ2=1+α2(ar+(b1-b2)c).由于b1>b2,显然λ1>1,λ2>1,均衡点E0是不稳定的结点. 在E1处它的特征值为λ1=1-α1(am+(b1-b2)c),由于b1>b2,显然λ2>1,故均衡点E1不稳定.类似地,可证均衡点E2不稳定. E*为纳什均衡点,它的Jacobian矩阵为 系统的稳定域由Jury条件[12]确定: 式中:Tr(J)和Det(J)分别表示J(E*)的迹和行列式. 设a=400,θ=0.6,b1=5,b2=3,c=30,此时均衡解为,解出稳定域为0<α1<2/625, 0<α1<2/675,可以画出系统(11)的稳定域如图3所示. 图3 集中决策下纳什均衡点稳定域Fig.3 Nash equilibrium region of stability under centralized decision 固定α2=0.001,可以画出价格pm、pr随α1变化的分岔图以及关于α1变化的最大Lyapunov指数图,并画出总利润πc随α1变化的分岔图,如图4所示. 从图4可以看出,在α1=0.002 7时,最大Lyapunov指数为0,此时价格pm、pr和利润πc均进入倍周期分岔,而在α1=0.004 095时,最大Lyapunov指数为正,说明系统开始进入混沌. 固定α1=0.001,可以画出价格pm、pr随α2变化的分岔图以及关于α2变化最大Lyapunov指数图,并画出总利润πc随α2变化的分岔图,如图5所示. 图4 价格pm、pr和利润πc随α1变化的分岔图及其最大Lyapunov指数图Fig.4 Bifurcation diagrams and largest Lyapunov exponent of pm,pr,πcwith respect to α1 从图5可以看出,在α2=0.002 55时,最大Lyapunov指数为0,此时价格pm、pr和利润πc均进入倍周期分岔,而在α2=0.004 032 5时,最大Lyapunov指数为正,说明系统开始进入混沌. 图5 价格pm、pr和利润πc随α2变化的分岔图及其最大Lyapunov指数图Fig.5 Bifurcation diagrams and largest Lyapunov exponent of pm,pr,πcwith respect to α2 在双渠道供应链中,建立关于价格的Stackelberg博弈,制造商是领导者,零售商是跟随者,决策变量为ω、pm、pr.博弈的顺序为:制造商首先决策批发价格ω和直销渠道价格pm使其利润πm最大,根据制造商制定的ω、pm,零售商再决策零售渠道价格pr,使其利润πr最大. 3.1 静态模型与分析 3.1.1 静态模型 根据逆向归纳法先求出博弈中零售商的最优决策解pr,再求出制造商的最优决策解ω、pm.对任意给定的ω、pm,零售商的最佳策略价格pr由∂πr/∂pr=0解得 把(13)式代入(6)式,因为制造商的利润πm是关于ω和pm严格凹的函数,所以由∂πm/∂ω=0和∂πm/∂pm=0,解得制造商的最优批发价格ω和直销渠道价格pm为: 把(14)式代入(13)式,得分散决策下零售渠道最优价格为: 把(14)和(15)式代入(5)和(6)式中得制造商和零售商利润为 3.1.2 静态模型分析 命题二:批发价和零售价与零售渠道忠诚度成正比,直销价与零售渠道忠诚度成反比. 证明:根据以上结果分析消费者对零售渠道的渠道忠诚度θ对分散决策下价格ωd、和的影响. 由此可见,批发价格和零售价格与零售渠道忠诚度成正比,直销价格与零售渠道忠诚度成正比,也就是说,随着θ的增加,批发价和零售价都增加,而直销渠道价格减少,这也是符合市场实际情况的.在双渠道供应链中,分析分散决策下零售渠道的渠道忠诚度对批发价格,直销渠道价格、零售渠道价格和制造商利润、零售商利润、供应链利润的影响,取参数a=400,b1=5,b2=3,c=30,可得图6. 图6 分散决策下零售渠道的渠道忠诚度θ对价格和利润的影响Fig.6 Influence of retail channel loyalty on price and profit under decentralized decision 由图6可以看出,在分散决策模型下,当θ∈(0.15,0.5)时,满足ω 命题三:分散决策下的直销价格与集中决策下的直销价格相等,分散决策下的零售价格大于集中决策下零售价格;分散决策下供应链整体利润小于集中决策下的整体利润. 即在集中决策下能够获得更大的整体利润. 3.2 动态模型与分析 3.2.1 动态模型 分散决策下模型的调整策略如下: 其中,零倍商决策为 式中:β1为ω的调整系数;β2为pm的调整系数. 由系统(18)可见,制造商首先决策ω和pm,其调整参数为β1、β2,零售商看到制造商的决策后再来决策pr. 3.2.2 动态模型分析 类似集中决策下均衡点的证明,可以得出分散决策下E0、E1、E2是不稳定的,E*是Nash均衡解. 设a=400,θ=0.45,b1=5,b2=3,c=30,此时均衡解为,由Jury条件解出稳定域为0<β1<8/1275,0<β2<8/2173,则系统(18)关于参数β1、β2的稳定域如图7所示. 图7 分散决策下Nash均衡点稳定域Fig.7 Nash equilibrium region of stability under decentralized decision 固定β2=0.003,可以得到价格ω、pm、pr随β1变化的分岔图以及利润πm、πr、πc随β1变化的分岔图,如图8所示. 图8 价格ω、pm、pr和利润πm、πr、πc随β1变化的分岔图Fig.8 Bifurcation diagrams of ω,pm,prand πm,πr,πcwith respect to β1 由图8可以看出,当β1=0.003 18时,价格ω、pm、 pr和利润πm、πr、πc均进入倍周期分岔. 固定β1=0.001,可得价格ω、pm、pr随β2变化的分岔图以及利润πm、πr、πc随β2变化的分岔图,如图9所示. 图9 价格ω、pm、pr和利润πm、πr、πc随β2变化的分岔图Fig.9 Bifurcation diagrams of ω,pm,prand πm,πr,πcwith respect to β2 由图9可以看出,当β2=0.002 7时,价格ω,pm,pr进入倍周期分岔;当β2=0.003 57时,利润πm,πr,πc进入倍周期分岔. 针对双渠道供应链,本文建立了集中决策和分散决策下制造商与零售商的静态和动态博弈模型.通过静态模型下解析结果的分析和比较,得出了零售渠道忠诚度对定价决策的影响,并利用稳定域图、分岔图、最大Lyapunov指数图研究了动态模型的复杂动力学性质.研究结果表明:集中决策下,整体供应链能够获得更大的利润.对本文进一步的讨论可以考虑旧产品的回收以及供应链契约协调等情形. [1]TSAY A,AGRAWAL N.Channel conflict and coordination in the E-commerce age[J].Production and Operations Management,2004,13(1):93-110. [2]SWAMINATHAN J M,TAYUR S R.Models for supply chains in e-business[J].Management Science,2003,49(10):1387-1406. [3] 周海云,杜纲,安彤.政府干涉下双渠道营销的闭环供应链协调[J].华东经济管理,2014,28(1):138-142. [4]徐广业,张旭梅.地区差异下多渠道供应链的定价决策[J].统计与决策,2014(2):48-51. [5]王媞,吴广谋.双渠道供应链促销努力与定价关系研究[J].现代经济信息,2014(1):87-88. [6]KUMAR N,RUAN R.On strategic pricing and complementing the retail channel with a direct internet channel[R].University of Texas at Dallas,2002. [7]HENDERSHOTT T,ZHANG J.A model of direct and intermediatedsales[R].California,USA:UniversityofCalifornia,Berkeley,2004. [8]GUO Y,MA J.Research on game model and complexity of retailer collecting and selling in closed-loop supply chain[J]. Applied Mathematical Modelling,2013,37(7):5047-5058. [9]MA J,WANG H.Complexity analysis of dynamic noncooperative game models for closed-loop supply chain with product recovery[J].Applied Mathematical Modelling,2014,38:5562-5572. [10]YUE X,LIU J.Demand forecast sharing in a dual-channel supply chain[J].European Journal of Operational Research,2006,174(1):646-667. [11]HUANG W,SWAMINATHAN J M.Introduction of a second channel:implica-tions for pricing and profits[J].European Journal of Operational Research,2009,194(2):258-279. [12]YASSEN M T,AGIZA H N.Analysis of a duopoly game with delayed bounded rationality[J].Applied Mathematics and Computation,2003,138:387-402. Complexity analysis of game model in a dual channel supply chain ZHANG Fang,ZHANG Ting-ting,MA Xiao-lin We consider a dual channel supply chain(CLSC),which is composed of one manufacturer and one retailer.We characterize the static and dynamic game models in a centralized and a decentralized dual channel supply chain. Then,we evaluate the influence of the degree of retail channel loyalty on pricing decision under the static model. Through numerical simulation,we analyze the complex dynamic phenomena,such as the stability region,chaos,bifurcation diagram and the largest Lyapunov exponent diagram.We find that the retail channel loyalty has a positive effect on the retail price and an inversus effect on the direct price;the retail price in decentralized supply chain is greater than that in centralized supply chain;the whole supply chain can get more profits under centralized decision. dual channel supply chain;game model;channel loyalty;pricing;chaos F274;F224 A 1671-024X(2015)03-0078-07 10.3969/j.issn.1671-024x.2015.03.017 2014-12-09 国家自然科学基金资助项目(61273231) 张 芳(1974—),女,博士,副教授.研究方向为复杂系统理论在经济上的应用.E-mail:zhangfangsx@163.com
2 集中决策(模型C)


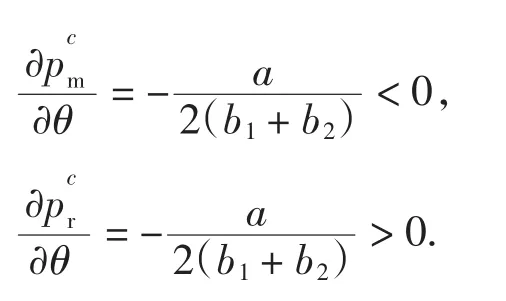







3 分散决策(模型D)


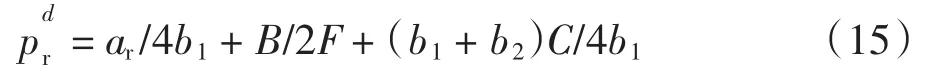

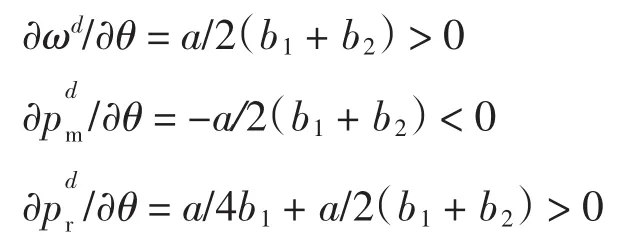




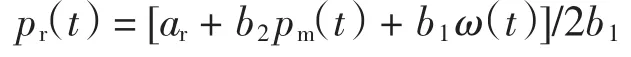




4 结论
(School of Science,Tianjin Polytechnic University,Tianjin 300387,China)
