同质企业研发竞争行为的动力学性态分析

黄东卫，付玉霞，于沈新

（天津工业大学理学院，天津 300387）

同质企业研发竞争行为的动力学性态分析

黄东卫，付玉霞，于沈新

（天津工业大学理学院，天津 300387）

应用非线性动力系统中的分岔和混沌理论及相关的经济学理论，建立了同质三寡头R&D（研究与开发）竞争在有限理性预期下的动力学模型，分析了该系统的均衡点及其稳定性，并以投入调整速度及技术溢出水平为控制参数，分析了系统产生分岔及混沌状态的条件，进一步得到了寡头间博弈引起的利润变化性态；结合Mathematics对不同参数条件下的系统进行了数值模拟，发现当企业的R&D投入调整速度过大时，系统由稳定状态进入倍周期分岔进而进入混沌状态；随着企业的技术溢出水平增大，其自身的利润下降，竞争对手的利润上升.模拟结果表明企业的利润在稳定状态下是稳定变化的，在混沌状态下则是连续波动的；当企业的投入调整速度过大时，其自身的平均利润呈下降趋势，竞争对手的平均利润呈上升趋势.

同质企业；竞争行为；动力学性态分析；研究与开发；有限理性；分岔；均衡点；Lyapunov指数；技术溢出

研究和开发（R&D）已经成为企业发展的主力，是企业核心竞争力和科技提升的重要科技手段.企业开展R&D活动可以获取更低的生产成本，更高的生产效率，从而获取更大的利润.然而，企业的R&D成果具有公共产品的部分属性，这就意味着在进行R&D活动的过程中，一定存在着技术溢出.技术溢出效应是经济市场中不可避免的现象，所以，这个因素也是不可忽略的.中外学者对此做了很多研究.J.A.Schum Peter创新的技术理论推动了R&D的相关研究的发展.Dssgupta根据创新收益的不同结构，把R&D分为竞争和非竞争两种类型.D’Aspremont和Jac-quemin最早研究了R&D合作问题，提出了R&D两阶段理论[1]. Ziss（1944）和Bischi（2002）建立了具有技术溢出水平的R&D博弈模型[2].Trshler[3]和Luckraz[4]从外生溢出的角度讨论了R&D的竞争和合作.国内不少学者对R&D的决策问题也做了一些研究.霍沛军等[5]研究了双寡头R&D合作与非合作时最优溢出问题.盛昭瀚等[6]运用非线性动力系统理论对R&D投入动态竞争系统进行了复杂性分析.胡荣等[7]对异质产品双寡头企业R&D最佳技术含量的博弈进行了分析.然而，多数文献主要研究了双寡头R&D的决策问题，对于三维、四维等更高维寡头之间的竞争却研究较少.而真实的市场中往往都是多于两个寡头的竞争.本文对不同溢出水平下有限理性同质三寡头的两阶段动态竞争模型作了复杂性分析，并用数值模拟分析了投入速度、技术溢出水平对企业利润及平均利润的影响.

1 模型的建立

假设市场上竞争的三寡头企业生产的产品是同质的，竞争中存在技术溢出.由 D’Aspremont和Jacquemin的经典R&D两个阶段研究：R&D活动分为R&D投入和产量决策两个阶段.同时，假设三企业的R&D投入都是有限理性的，即企业第二阶段的决策是根据边际利润效应做出判断的.

设第i家企业（i=1，2，3）在t时期的价格为pi（t），qi（t）表示企业i（i=1，2，3）在t时期生产的产品产量，市场的总产出Q（t）=q1（t）+q2（t）+q3（t）.设三企业在t时期的逆需求函数为pi（t）=a-bQ（a，b＞0）.其中：a为市场最高价；b为市场需求弹性.设第i家企业（i=1，2，3）在t时期的第一阶段的研究投入量为xi（t）（≥0）.博弈过程中存在着技术溢出，为了讨论方便，设企业i对企业j和企业k的技术溢出水平都为αi（0≤α≤1；i，j，k=1，2，3；i≠j≠k），则企业i通过企业j和企业k的技术溢出使本企业的投入增加量为αixj（t）+αkxk（t）.设未进行R&D活动时的三企业的单位产品成本均为c，开展R&D活动后企业i单位产品的成本减少量为εijk（t）=β（xi（t）+αjxj（t）+αkxk（t））（β≥0），则成本变为Ci（t）=c-εijk（t）.本文假设企业i的研究投入的成本是非线性的：

于是三企业在t时期第二阶段的利润函数为

把（2）代入（1）得在t时期第一阶段企业i选择投入量为xi（t）（i=1，2，3）时利润最大，为

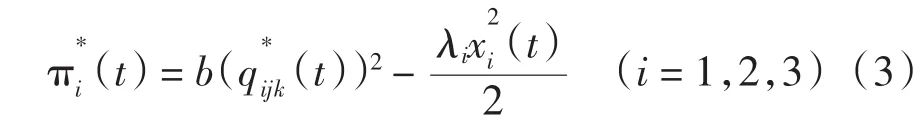
又知3个企业都采用有限理性预期，企业的研究投入不是通过精确计算得出的使利润最大化的决策，而是根据边际利润做出判断，边际利润大于零时，企业进行投入，边际利润小于零时，企业不投入，于是企业在t+1期的投入量为

式中：γi＞0（i=1，2，3）为企业i在博弈过程中R&D投入调整速度.由式（1）—式（4）得到同质三寡头R&D博弈动态模型为：

2 不动点及局部稳定性分析

为了研究系统的不动点的局部稳定性，首先计算系统（5）的雅克比矩阵

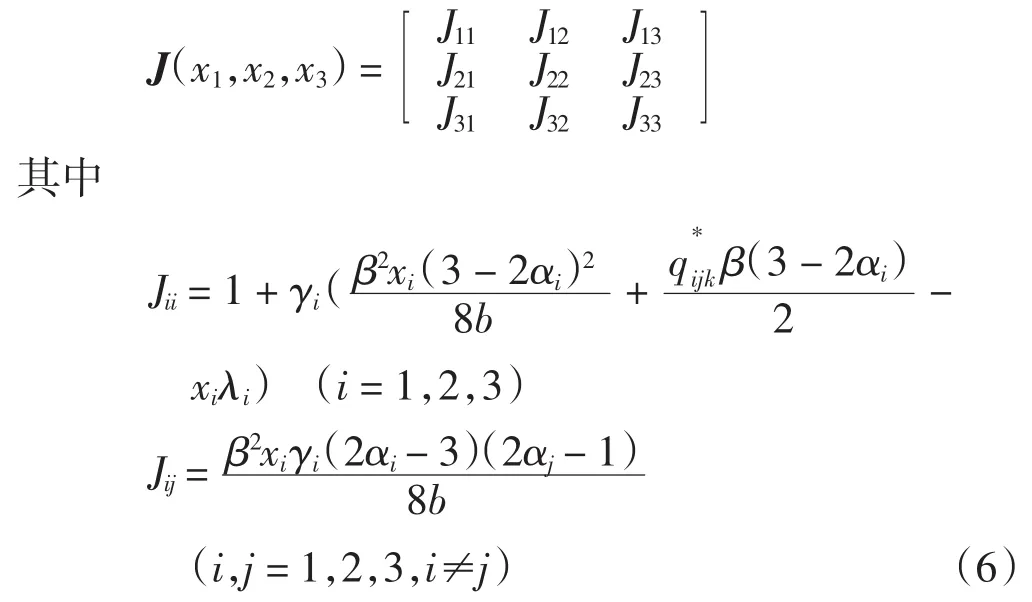
令xi（t+1）=xi（t），求得系统的解析解比较繁琐，为了简便，给某些参数赋值.取α1=0.3，α2=0.2，α3=0.25，β=1.2，λ1=2，λ2=2.3，λ3=2.2，a=30，b=2，c=4得到系统的8个不动点E1（0，0，0）E2（0，0，2.977 1）E3（0，2.997 2，0）E4（0，2.807 3，2.745 7）E5（3.158 6，0，0）E6（2.910 7，2.836 1，0）E7（2.953 8，0，2.814 8）E8（2.735 6，2.665 5，2.607 0）.显然，这些不动点和γi（i=1，2，3）无关；其中Ei（i=1，2，3，4，5，6，7） 称有界均衡点，E8是唯一的Nash均衡点[8-9].

定理 有界均衡点Ei（i=1，2，3，4，5，6，7）是不稳定均衡点.

证明 将E1（0，0，0）代入雅克比矩阵得

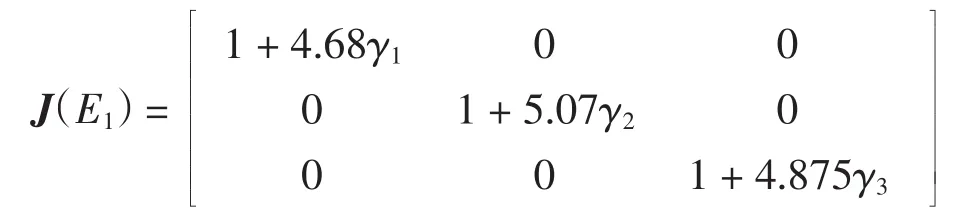
则它的特征值分别是1+4.68γ1，1+5.07γ2，1+4.875γ3，又因为参数γi＞0（i=1，2，3），所以这3个特征值的模都是大于1的，所以该不动点是不稳定的.

同理，将Ei（i=1，2，3，4，5，6，7）分别代入雅克比矩阵计算出它们各自的特征值（不再一一列举出来），结果发现特征值的模都至少有一个大于1[10]，即Ei（i=1，2，3，4，5，6，7）是不稳定的.

下面讨论Nash均衡点E8的稳定性情况，将E8代入雅克比矩阵得

它的特征方程为f（λ）=λ3+Aλ3+Bλ+C，其中

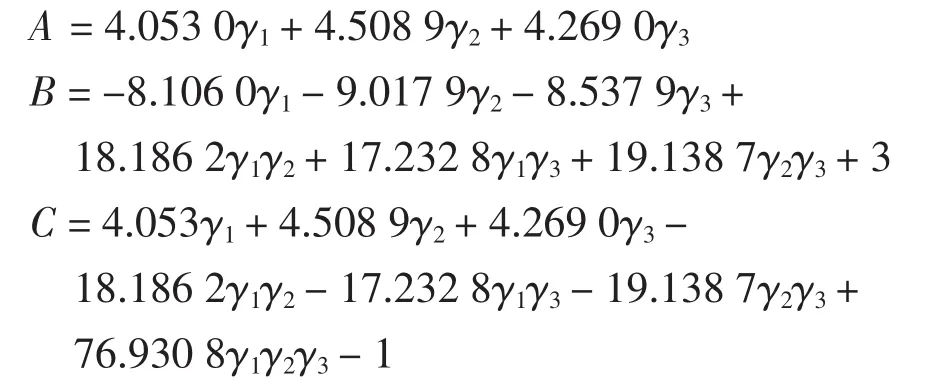
根据Routh-Hurwitz稳定性判据，系统在E8渐近稳定的充要条件是特征方程的所有零点落在复平面的单位圆内，必须满足以下4点[11]

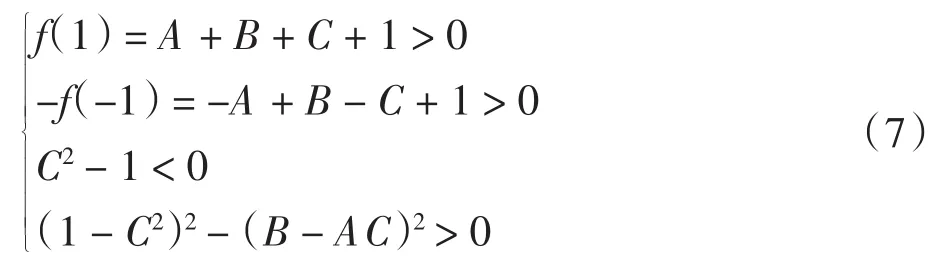
根据式（7）解出来的γi（i=1，2，3）就是系统的稳定区域.稳定的Nash均衡点表明：尽管三寡头初始的R&D投入量不同，但是经过重复博弈，企业每次对初始投入量的调整最终将稳定在Nash均衡点处的稳定的投入量水平，一旦企业的调整速度超出了稳定区域，系统就会进入倍周期分岔甚至混沌状态.

3 数值模拟及模型的复杂动力学特性分析

为了更好地了解系统（5）的动态演化过程，识别系统的混沌行为[12-13]，本文采用数值模拟来分析.给出部分参数的值，作出R&D投入量的分岔图和李雅普诺夫指数谱.取数值模拟的初始参数值为α1=0.3，α2=0.2，α3=0.25，β=1.2，λ1=2，λ2=2.3，λ3=2.2，a=30，b=2，c=4，γ2=0.3，γ3=0.4，3个寡头的初始R&D投入量分别是x1=1.7，x2=2，x3=2.1.

3.1 R&D投入调整速度对系统状态的影响

为了研究企业R&D的调整速度对系统（5）的状态影响，本文选取企业1的R&D调整速度作为研究对象，企业2和企业3的R&D的调整速度对系统（5）的影响可以用同样的方法做.企业1的R&D投入量的分岔图如图1所示.

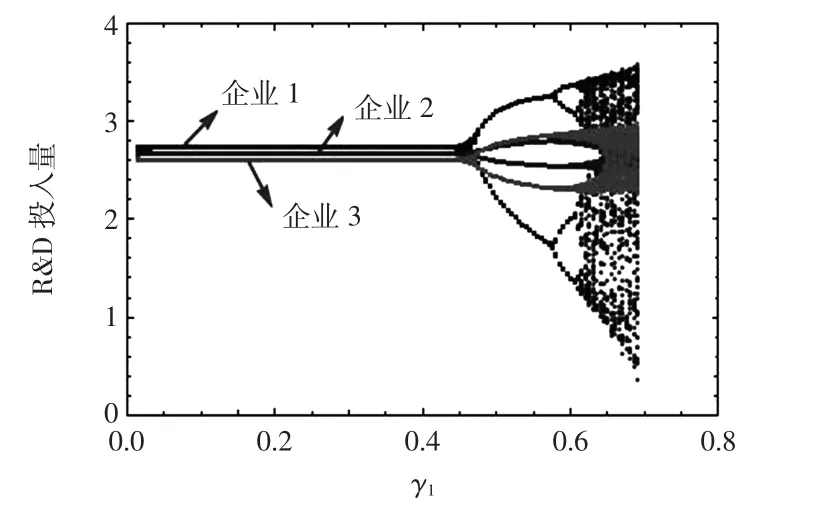
图1 R&D投入量的分岔图Fig.1 R&D input bifurcation diagram

观察图1可知，系统（5）随着企业1的R&D投入调整速度γ1的连续变化呈现稳定、倍周期分岔、混沌状态.γ1较小时，系统稳定；γ1较大时，系统出现分岔进而出现混沌状态.同时也可以用系统的Lyapunov指数谱（图2）进一步阐述该过程的变化趋势.Lyapunov指数是用来表征相轨道间分离快慢的指标，如果Lyapunov指数为正，则系统为混沌状态，如果Lyapunov指数为负，则系统处于稳定状态.

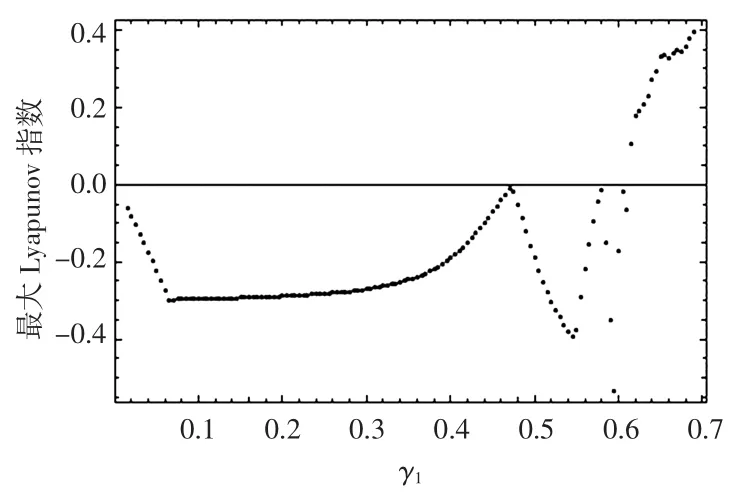
图2 系统的最大Lyapunov指数谱Fig.2 Maximal Lyapunov exponent of system

从图2可以看到，企业1的R&D投入调整速度γ1较小时，系统的最大Lyapunov指数小于零，系统处于稳定状态；γ1=0.49时，系统的最大Lyapunov指数等于零，系统进入倍周期分岔状态；当γ1增大到0.62时，系统的最大Lyapunov指数开始大于零，系统进入混沌状态.这与图1观察到的结果是一致的.

3.2 R&D投入调整速度对企业利润的影响

仍然以企业1的R&D投入调整速度为研究对象，模拟三寡头企业的利润在不同的γ1取值下，随博弈周期变化趋势图如图3所示.选取博弈周期T=100，分别取γ1=0.32和γ1=0.66，作出企业利润在这两个取值下的变化趋势图.由图1和图2知，γ1=0.32对应系统（5）的稳定状态，γ1=0.66对应系统（5）的混沌状态.

图3 三企业的利润变化趋势图及相图Fig.3 Changing profit of three enterprises and phase diagram

由图3（a）可知，γ1=0.32即系统处于稳定状态时，三企业的利润随博弈周期稳定变化；由图3（b）可知，γ1=0.32系统处于混沌状态时，三企业的利润连续波动.图3（c）和图3（d）是对应的三企业的利润的相图，γ1=0.32时相图基本是一条直线，说明利润稳定变化，γ1=0.32时相图是混沌吸引子，说明利润是波动的，这和图3（a）、图3（b）的结论的是一致的.

为了进一步说明企业1的R&D投入调整速度γ1、γ2和γ3对企业利润的影响，模拟企业平均利润在100个博弈周期内随着γ1、γ2和γ3的变化趋势图，如图4所示.

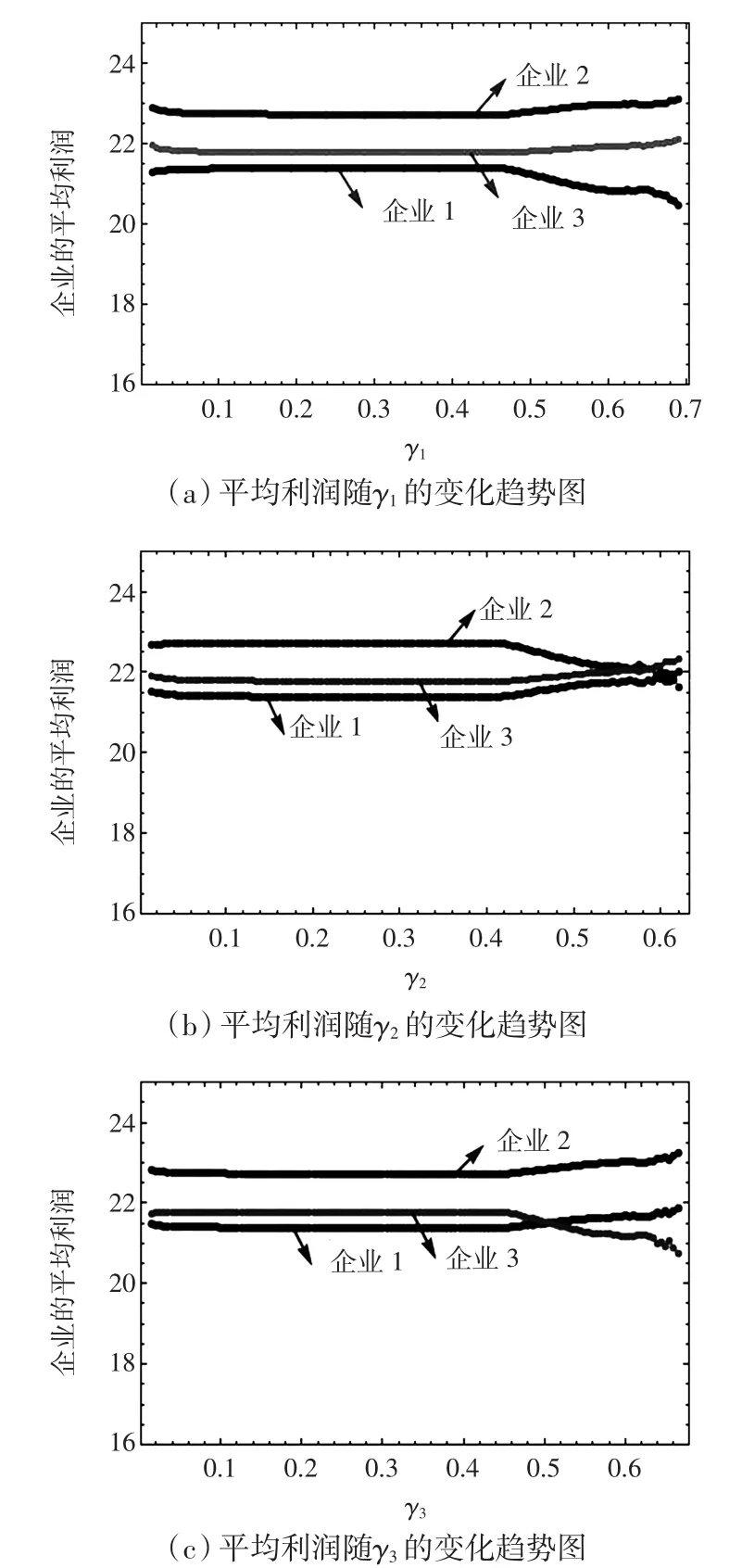
图4 平均利润随γ1、γ2、γ3时变化趋势图Fig.4 Average profit with change of γ1，γ2，γ3

从图4（a）可知，企业1 R&D投入调整速度γ1较小时，系统处于稳定状态，三企业的平均利润稳定变化；随着γ1的增大，系统进入倍周期分岔甚至混沌状态，企业1的平均利润呈下降趋势，但企业2与企业3的平均利润呈上升趋势.这说明企业的投入调整速度过大时对企业自身是不利的，对竞争对手是有利的，图4（b）与图4（c）也说明了这个结果.

3.3 技术溢出水平对企业平均利润的影响

以企业1的技术溢出水平α1为研究对象，分别选取α2=0.2和α2=0.6，α3=0.25和，α3=0.7，模拟三企业的平均利润随着α1的变化趋势图，其他参数不变，选择博弈周期T=100，见图5.

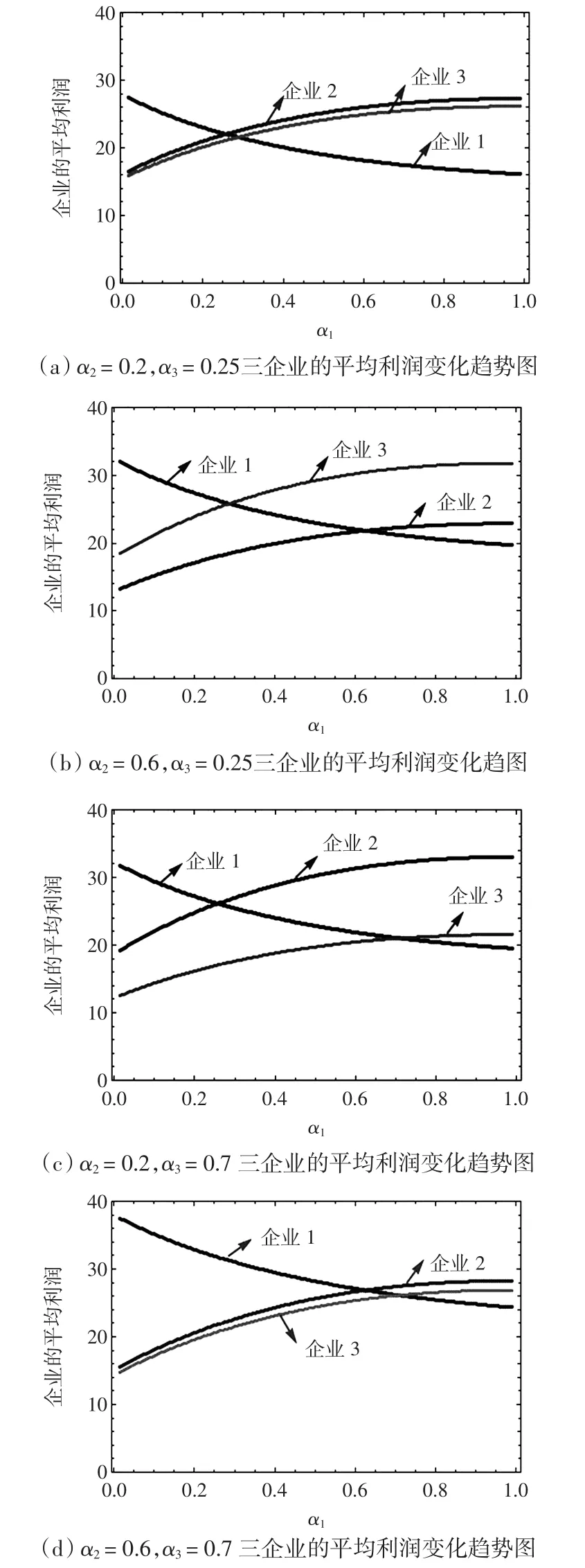
图5 三企业的平均利润随α1的变化趋势图Fig.5 Average profit of three enterprises with change of α1

比较图5（a）和图5（b）可以看出，当企业3的技术溢出水平固定为α3=0.25，企业2的技术溢出水平分别为α2=0.2和α2=0.6时，企业1的平均利润随着它自身的技术溢出水平α1的增加呈下降趋势；企业2和企业3的平均利润呈上升趋势；图5（b）中三企业的大体趋势和图5（a）是一样的，但是企业1和企业3的平均利润整体上高于图5（a）中企业1和企业3的平均利润，企业2的平均利润整体上则相对降低，同时企业2与企业3之间的平均利润差距变大.这说明，企业的技术溢出使自身利润下降，则对竞争对手是有利的.反过来，如果企业降低自己的技术溢出水平，对手的利润就会降低，由于竞争者同样的心理，对手也会降低自身的技术溢出水平来降低对方的利润，最终各企业将在技术溢出水平相等时达到博弈均衡.比较图5（a）和图5（c），图5（b）和图5（d）亦能得到同样的结论.

由此可见，企业之间是相互影响又相互依存的，只有企业间相互合作，达到知识共享，资源共享，技术共享，优势互补，才能共赢，才能为社会创造更多的财富和价值.

4 结束语

本文建立了不同溢出水平下同质三寡头在有限理性预期下R&D竞争模型，对此模型作了复杂的动力学分析，发现当企业的R&D投入调整速度过大时，系统由稳定状态进入倍周期分岔进而进入混沌状态；随着企业的技术溢出水平增大，它自身的利润下降，对手的利润上升，对手的技术溢出水平变大时，它的利润也会相对变大.同时用数值模拟分析了企业的R&D投入调整速度及技术溢出水平对企业利润和平均利润等的影响.结果表明：企业的利润在稳定状态下是稳定变化的，在混沌状态下则是连续波动的；企业的平均利润与自身的调整速度密切相关，当某个企业调整速度过大时，自身的平均利润呈下降趋势，竞争对手呈上升趋势.企业在竞争的过程中，企业的技术溢出水平对自身和对对手的影响都是利大于弊的.企业间只有合作，形成资源共享，知识共享，技术共享才能共赢.本文仅就同质三寡头R&D之间的竞争做了一些分析，对于产品有差异性企业间的竞争，不同预期条件下企业间的竞争及更高维寡头之间的竞争没有作分析，这些问题还需要进一步的研究.

[1]D′ASPREMONT C，JACQUEMIN A.Cooperative and non-cooperative R&D in a duopoly with spillover[J].The American Economic Review，1988；78（5）：1133-1137.

[2]ZISS S.Strategic R&D with spillover，collusion and welfare[J]. The Journal of Industrial Economics，1994（4）：375-397.

[3]MILSTEIN T.R&D wars and the effects of innovation on the success and survivability of firms in oligopoly markets[J].Int J Ind Organ，2009，27（4）：519-531.

[4]LUCKRAZ S.R&D games in a Cournot duopoly with isoelastic demand functions：A comment[J].Econ Model，2011，28（6）：2873-2876.

[5]霍沛军，陈剑，陈继祥.双寡头R&D合作与非合作时的最优溢出[J].中国管理科学，2002，10（6）：92-96.

[6]盛昭瀚，李煜，陈国华，等．企业RD投入动态竞争系统的全局复杂性分析[J].管理工程学报，2006，9（3）：1-10.

[7]胡荣，陈圻，王强.双寡头动态R&D竞争的复杂性研究[J].管理工程学报，2011（2）：2740-2746.

[8]NASH J F.Equilibrium points in N-person games[J].Proceedings of the National Academy of science of the United States of Am-erica，1950，36：48-49.

[9]NASH J F.Non-cooperative games[J].Annals of Mathematics，1951，54：286-295.

[10]LI C，PENG J，HUANG Q.Controlling synchronization of chaos and hyperchaos systems[J].J Northeast Norm Univ Nat Sci，2001，33（3）：43-47.

[11]王翼.自动控制中的基础数学—微分方程与差分方程[M].北京：科学出版社，1987：238-242.

[12]浦小松.一类寡头垄断市场产量博弈及混合模型的动力学研究[D].天津：天津大学，2012.

[13]PECORA L M，CARROLL T L.Synchronization in chaotic systems[J].Phrsics Review Letter，1990，64（8）：821-824.

Dynamics analysis of state of homogenous corporate R&D competition

HUANG Dong-wei，FU Yu-xia，YU Shen-xin
（School of Science，Tianjin Polytechnic University，Tianjin 300387，China）

We apply the theory of bifurcation and chaos of nonlinear dynamical systems and related theory of economics，and then establish a R&D competition dynamic model under the limited rational expectations of three homogeneous oligarchs and analyze this system′s equilibriums and their stability.We also take adjusting speed of R&D input and technical spillovers level as the control parameter and analyze the condition of the system bifurcation and chaos，then we get the changing behavior of profit as competition among oligarchs；Under the condition of different parameters we simulate the system by Mathematics and illustrate the result.We find that when the adjusting speed of R&D input of the enterprise is too large，then the system becomes from stable state into period-doubling bifurcation and chaotic state.As the technical spillovers level of the enterprise increases，its profit falls and the opponent′s profit rises.In addition，the results of simulation show that enterprise′s profits changes steadyly under the stable state and changes valatily，under the chaotic state.When the adjusting speed of input of the enterprise is too large，its average profit falls and the opponents′rises.

homogenous corporate；competition；dynamics analysis；research and development（R&D）；bounded rationality；bifurcation；equilibriums；Lyapunov index；technical spillovers

F274；F224

A

1671-024X（2015）03-0073-05

10.3969/j.issn.1671-024x.2015.03.016

2014-12-11

国家自然科学基金资助项目（11102132）

黄东卫（1966—），男，教授，博士，研究方向为随机动力系统理论及应用.E-mail：tjhuangdw@163.com