树脂浇注干式变压器三维温度场仿真计算

张 牧，高立业，魏 娟，修春波

（天津工业大学电气工程与自动化学院，天津 300387）

树脂浇注干式变压器三维温度场仿真计算

张 牧，高立业，魏 娟，修春波

（天津工业大学电气工程与自动化学院，天津 300387）

为便于诊断干式变压器的故障，对干式变压器进行热点分析.根据干式变压器实际结构建立了三维对称热传导模型，并基于多物理场有限元软件平台Comsol Multiphysics对干式变压器开展温度场仿真计算，计算得出温度场分布云图以及铁芯、绕组温升曲线.通过比对实际数据和仿真分析结果，从而确定温度分布及最热点温度位置在低压绕组距底部2/3处，可为该类干式变压器的在线诊断及结构优化设计提供理论依据.

干式变压器；流体温度场；热点温度；有限元仿真

树脂浇注干式变压器因具备防火、防爆、运行可靠、维护方便、体积小等显著优点，已在城市高层建筑、石油、化工煤矿等场所得到了广泛的应用[1-2].然而，在干式变压器容量不断增加的同时，发热和冷却问题也逐渐的凸显出来，并成为影响其安全运行的主要因素.研究表明，干式变压器的运行不稳定或毁坏主要是由于变压器的绕组温度超过绝缘材料的耐热极限[3-4]，其中对于A级绝缘的变压器温度，每增加8℃，变压器绝缘老化速度将增加一倍[5].绕组过热不仅会造成绝缘的加速老化进而影响其寿命，而且会引发严重的安全问题，国内外每年都会发生因为绕组过热造成一系列恶性事故，导致了巨大的经济损失[6-8].因此对干式变压器进行热点分析显得尤为重要，不仅可以维护干式变压器的正常安全运行，同时也为该类干式变压器的结构优化设计提供了理论依据.

国内外研究者经过多年研究，获得了许多对干式变压器生产设计具有重要指导意义的研究成果，大部分是关于干式变压器稳态运行状态下的温度场分布特性的研究[8-11].在数值仿真计算方法中，国内的许多专家学者也做了大量的尝试，在二维温度场模拟方面取得了一定成果[12-13]，但由于变压器的热问题涉及传热学、流体力学、电磁学等多学科知识，其复杂性和试验难度限制了对其全面的研究，尤其是三维温度场立体建模目前研究还十分有限，尚未有能够全面反映出干式变压器的整体温度场模型.本文针对以上问题，根据干式变压器实际结构建立了三维面对称热传导模型，基于Comsol平台对干式变压器开展温度场仿真计算，并结合传热学理论对干式变压器温度场分布情况进行理论分析，找出干式变压器运行中的最热点温度的位置，为热点温度传感器及监测单元的安装点提供数据支撑.

1 温升计算

干式变压器运行时铁芯由于磁滞损耗、涡流损耗及绕组由于电阻和引线损耗等产生热量.其中一部分热量储存在干变的发热体中，使发热体本身温度升高，另一部分热量发散到周围介质中，使周围介质温度升高[14-15].热量向周围传递的方式可分为热传导、热对流和热辐射3种基本形式[16].而干式变压器内部的热量传递主要是通过热传导来实现的，同时在设备表面及外界环境间还存在着热对流和热辐射.干式变压器的温升主要包括铁芯温升和绕组温升.

1.1 铁芯温升计算

由于铁芯材料和结构的不同，其经验系数取值也不同.由硅钢片叠装的铁芯，计算其平均温升时，经验系数k、n分别取0.36和0.8[17]，铁芯温升按如下经验公式（1）计算：

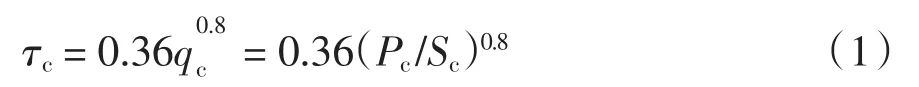
式中：τc为铁芯温升（℃）；qc为铁芯散热面单位热负荷（W/m2）；Pc为铁芯损耗（W）；Sc为铁芯的有效散热面积（m2）.

铁芯损耗Pc主要包括磁滞损耗Ph和涡流损耗Pe，由方程组（2）表示为：

式中：η为铁芯材料的磁滞系数；f为频率（Hz）；Bmax为最大磁通密度（T）；d为硅钢片厚度（cm）；V为铁芯体积（cm3）.η、Bmax、d、V都是材料的固有属性，可以通过变压器出厂手册进行查询，属于已知量，因此，只需测出频率就可以计算出铁芯的损耗.

1.2 绕组温升计算

低压和高压绕组的发热主要是由各自的负载损耗引起.负载损耗由基本损耗和附加损耗构成，其中基本损耗是指绕组导线的直流电阻损耗，是导致绕组温度升高的主要原因.因此，本仿真中负载损耗只考虑直流电阻损耗[18]，以简化计算过程，提高运算速度.

绕组温升计算公式由公式（3）给出：

式中：τw为绕组温升（℃）；qw为绕组散热面单位热负荷（W/m2）；Pw为绕组损耗（W）；Sw为绕组有效散热面积（m2）.n，k分别为经验系数，经验系数的取值由其散热条件确定.

本文所用干式变压器为树脂浇注型，低压绕组表面与气道直接接触，k取0.66，高压绕组采用分段层式，绕组中设有竖直气道，有2个轴向散热面，k、n分别取0.46与0.8.

绕组损耗计算公式由公式（4）给出：

式中：Pk为变压器短路有功功率（kW）；β为负载系数；Sjs为变压器计算负荷（kVA）；Se为变压器额定容量（kVA）.Pk、Se都是变压器固有参数，可以通过变压器出厂手册查询，属于已知量，因此，只要获得变压器的计算负荷便可以计算出绕组损耗.

2 温度场的边界条件

在仿真计算中，模型合理的物理过程与边界条件是保证计算稳定收敛、结果正确的基础.为了使导热微分方程产生唯一解，则需要对微分方程设置符合实际情况的边界条件和初始条件.边界条件指导热体的表面与周围介质间的热量交换状况.在进行温度场分析时，第三类边界条件最为常见.本文所研究的干式变压器三维流体温度场具有热对流和热辐射过程，是典型的第三类边界条件，对于干变绕组间气道的辐射与对流相比，可认为辐射小到可以忽略[18]，表示如式（5）所示：

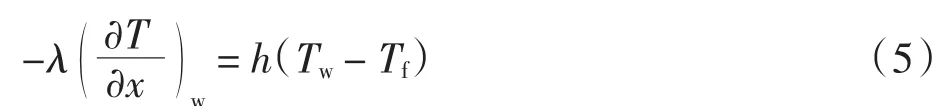
式中：h为对流换热系数（W/（m2·K））；Tw为物体表面温度（K）；Tf为流体温度（K）.

3 温度场仿真分析

本仿真对象为一台实际干式变压器，型号为SCB35-1000/35，电压等级为35±3×2.5%/10.5 kV，绝缘等级为F级.此干式变压器的结构为低压绕组置内，采用铜箔绕制而成，低压绕组和铁芯、高压绕组之间分别设有气道进行散热.高压绕组采用扁铜线绕制成分段多层圆筒式，共分为4段，中间浇注绝缘树脂，高、低压绕组两端各有一定厚度的绝缘端封.干式变压器三维结构示意图及三维有限元模型分别如图1和图2所示.

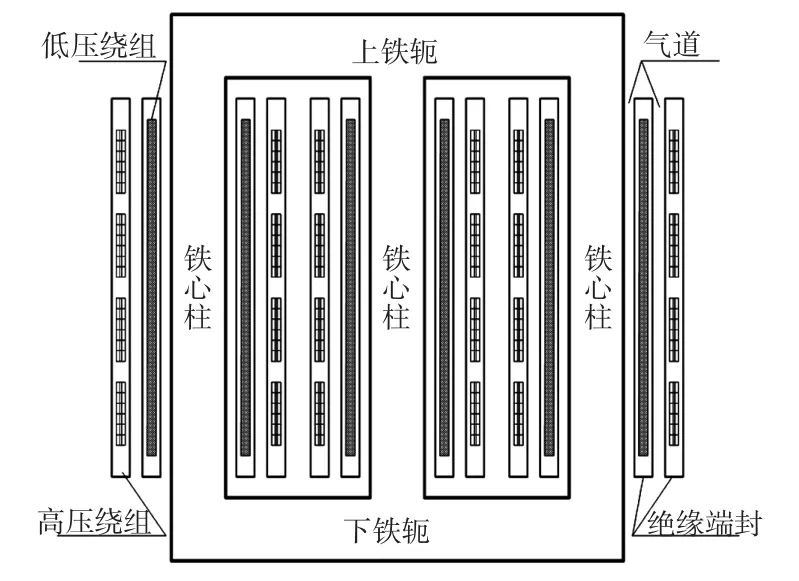
图1 干式变压器三维结构图Fig.1 Three-dimensional structure of dry-type transformer

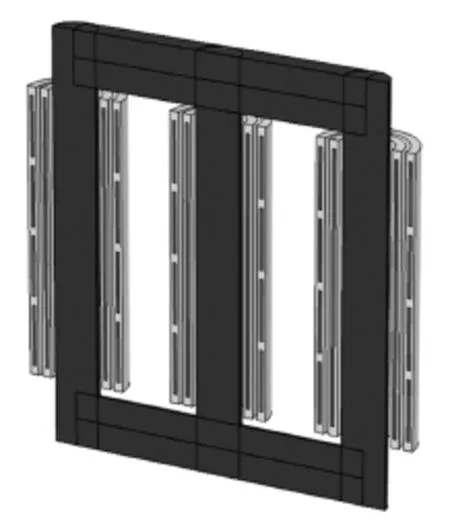
图2 干式变压器三维有限元模型Fig.2 Three dimensional finite element model of dry type transformer

为了尽量还原干式变压器的实际结构并兼顾仿真计算的快捷性，在建立仿真模型时，以干式变压器中轴平面为对称平面建立1/2面对称模型，这样既保证了实际结构的正确又节省了仿真计算时间，其他结构中的部分简化为：

（1）变压器内部热源为铁芯、低压绕组、高压绕组，其截面近似为圆柱体，本仿真将铁心当做圆柱体.

（2）假定变压器置于一个气流方向竖直向上，且流速一定的空间中.

3.1 干式变压器材料属性设定

根据实际干式变压器各部分使用的材料设置材料的导热系数，如表1所示.

表1 干式变压器材料导热系数Tab.1 Material coefficient of thermal conductivity of dry type transformer

3.2 施加载荷

仿真计算所施加的载荷条件主要包括变压器运行时各部分产生的损耗以及环境温度.仿真数据是实际变压器厂所提供的1 000 kVA的树脂浇注式干式变压器在额定运行状态下计算出的变压器铁芯、高低压绕组的损耗.具体载荷数据如表2所示.

表2 干式变压器施加载荷数据Tab.2 Dry-type transformer load data

3.3 网格划分

干式变压器的流体温度场模型较为复杂，在进行网格划分时需要采用多重网格划分方法.网格尺寸的大小决定着仿真结果的精确度.网格划分越细计算结果越准确，但对计算机的要求也就越高.实际处理中，往往采用分区域不同密度剖分方法以实现计算精度与速度的兼顾.为了准确的反映干式变压器内部温度场分布情况，根据变压器的结构，依据重点部位网格细划的原则，分别对铁芯、高、低压绕组及树脂绝缘设定不同的网格划分尺寸.本仿真共有网格单元109 314个.网格剖分如图3所示.

图3 干式变压器网格划分图Fig.3 Mesh of dry type transformer

3.4 仿真结果

本次仿真在室温28℃以下模拟了干式变压器在100%负荷运行情况下，干式变压器三维流体温度场的分布特性，最后将干式变压器温度场仿真结果与实测温度值进行比对，其整体温度场分布如图4所示.

由图4可见，干式变压器内部温度场分布规律为从底部到顶部温度变化基本是由低到高再到低，内侧温度高于外侧，最热点位于干式变压器低压绕组距底端2/3处附近，其值为81.2℃，低于F级绝缘极限温升100℃.取变压器的B相作为研究对象，分别绘制B相铁芯、低压和高压绕组的温度分布曲线，如图5所示.

由图5可知，低压绕组相对于铁芯和高压绕组温升较高，是因为低压绕组处于铁芯和高压绕组之间，其散热方式主要通过气道内空气对流将热量带走，而高压绕组处于外侧不仅可以通过对流散热，还可以以辐射散热，散热效果明显优于低压绕组.由图5（a）可知，铁芯底部温度上升比较缓慢，而后迅速上升，主要原因是外侧的低压绕组对其产生的影响.

图4 温度场分布图Fig.4 Temperature field distribution

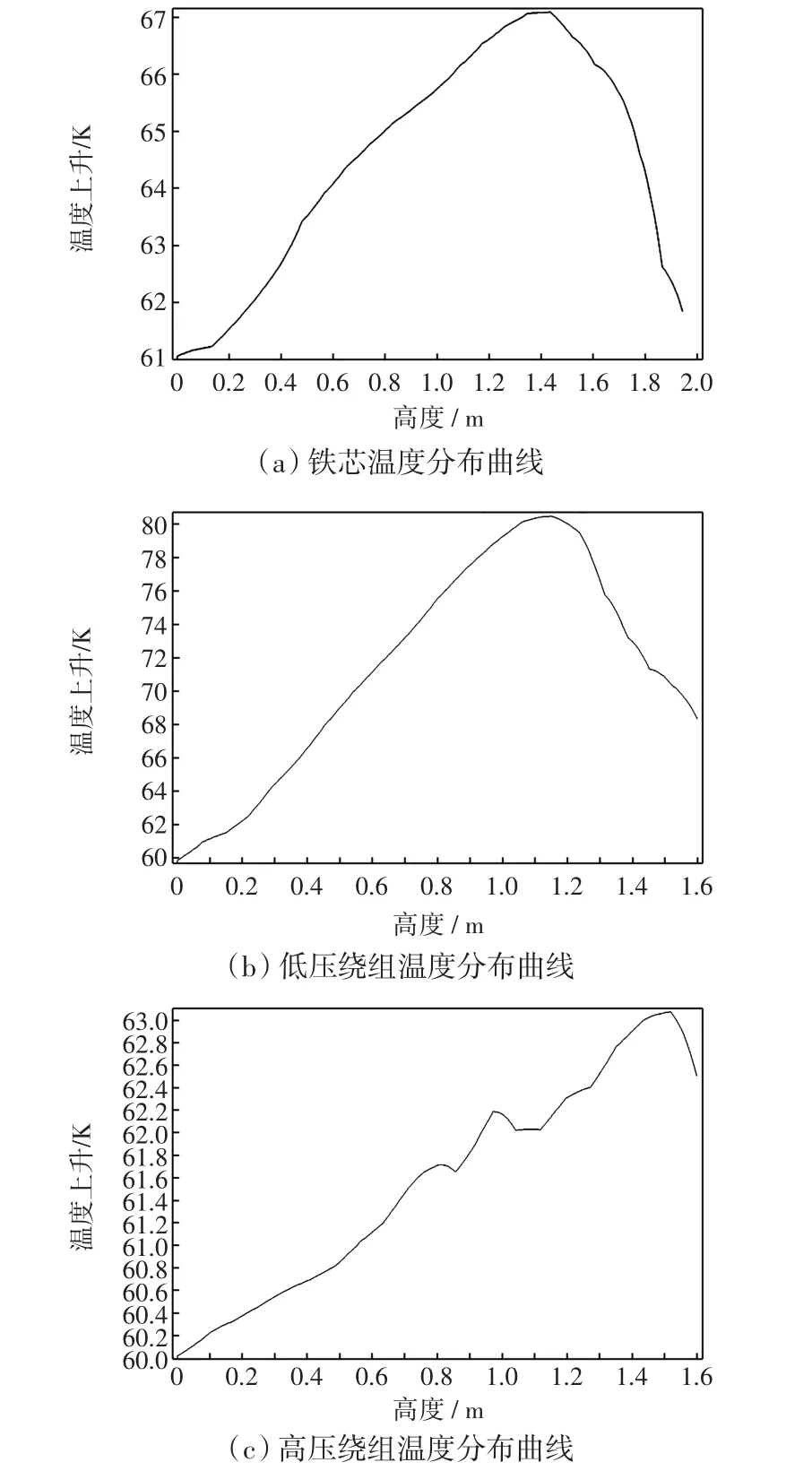
图5 干式变压器B相铁芯、低压和高压绕组温度分布曲线Fig.5 B iron core dry-type transformers，low voltage and high voltage winding temperature distribution curve

由图5（c）可知，高低压绕组上半部的散热效果比下半部散热效果差，在分段绝缘的地方温度稍微下降，但绕组温度总体沿轴向升高，这是由于绝缘的地方没有内部生热，绕组内部温度不能持续上升，所以温度略有下降.同时由于空气在高低压绕组之间形成的气道中流动，空气受热后温度升高，体积膨胀，会沿着气道向上自由流动.

最热点部位绝缘性能的好坏直接影响干式变压器的安全运行情况.仿真结果表明，干式变压器的最热点部位为内部绝缘弱的部位，因此，在设计干式变压器时应加强此处的绝缘性能，或加强此处的通风效果.同时，在监测干式变压器时，可以对此处温度进行监测.

4 仿真结果验证

通过利用干式变压器中预埋好的温度传感器采集干式变压器在运行过程中的关键点温度信息，并在实际结构建立的仿真模型中同样的部位设定温度检测点.通过将仿真计算所得的温升值与实际运行过程所采集的温度信息进行比较，以此来验证仿真结果是否能满足实际工程的需要.试验热电偶布置在B相的情况如图6所示.

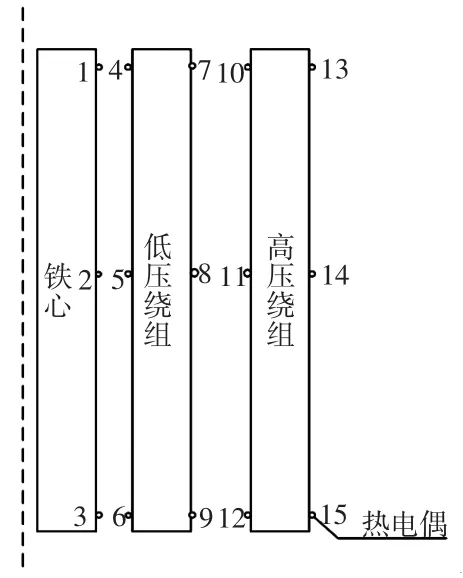
图6 热电偶布置情况Fig.6 Thermocouple arrangement

热电偶布置采用对称结构设定，这样采集可以最大程度的反映出干式变压器的温度信息.铁芯、低压和高压绕组之间都留有空气气道，分别将热电偶按干式变压器纵向高度三等分放置.仿真计算数值与实测数值比较结果如表3所示.通过比较结果可知，仿真计算所得数值与温度传感器所测数值基本一致，相对误差表示为：

式中：δ为相对误差；x*为计算值；x为实测值.经计算相对误差在3%以内，满足工程应用的要求.

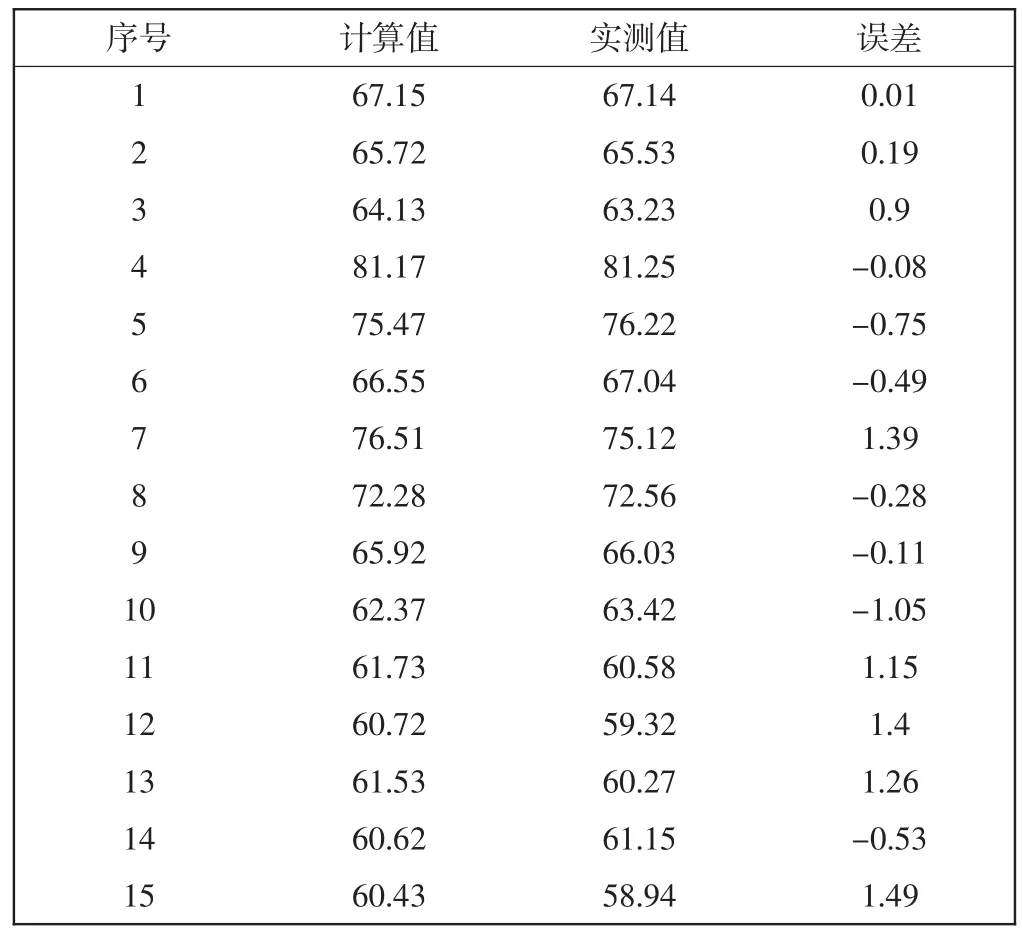
表3 计算值与实测值的比较Tab.3 Comparison of calculated and measured values

5 结论

本文针对二维仿真不能全面反映干式变压器热点温度场的问题，建立了三维轴对称热传导模型，基于Comsol平台对干式变压器开展温度场仿真计算.仿真结果表明，变压器从底部到顶部温度变化基本是由低到高再到低，内侧温度高于外侧，最热点位于干式变压器低压绕组距底端2/3处附近，最热点温度约为81.2℃.结合传热学与变压器实际结构分析，给出了干式变压器运行中的最热点温度的位置，为热点温度传感器及监测单元的安装点提供数据支撑，最后本文将仿真计算的结果与实测值比较，仿真计算所得数值与温度传感器所测数值基本一致，并且误差均在3%以内，满足工程应用的要求.本研究成果可为生产设计以及运行提供理论基础与数值参考.

[1] 姚志松，姚磊.新型配电变压器结构、原理和应用[M].北京：机械工业出版社，2006.

[2]袁臣虎，张牧，高圣伟，等.基于DSP+ARM的干式变压器状态监测系统硬件设计[J].天津工业大学学报，2011，30（4）：77-80.

[3]李春华，梁作德，苏宝国，等.干式变压器温度场的有限元仿真计算[J].变压器，2012，49（10）：7-10.

[4]姚育成，蔡定国，徐业彬，等.干式变压器温度场数值模拟[J].变压器，2012，49（8）：2012，49（8）：31-33.

[5] 陈洪波，李旻.基于传感器的输变电设备状态监测技术[M].西安：西安交通大学出版社，2014.

[6]熊兰，赵艳龙，杨子康，等.树脂浇注干式变压器温升分析与计算[J].高电压技术，2013，39（2）：265-271.

[7]ESLAMIAN M，VAHIDI B，ESLAMIAN A.Thermal analysis of cast-resindry-typetransformers[J].Energy Conversion and Management，2011，52（3）：2479-2488.

[8]EBRAHIM R，DAVOOD A.Analysis of temperature distribution in cast-resin dry-type transformers[J].Electrical Engineering，2007，89（5）：311-319.

[9] 陈世省，陈秀菊.树脂浇注干式变压器绕组最热点位置的分析[J].变压器，2002，39（9）：8-11.

[10]范春桥，张重远.10 kV干式变压器温度场仿真计算与寿命评估[D].保定：华北电力大学，2012.

[11]刘小波，姚芳.干式变压器漏磁场及温度场的分析与研究[D].天津：河北工业大学.2012.

[12]赵艳龙，熊兰.树脂浇注干式变压器温度场数值计算及在线监测系统研究[D].重庆：重庆大学.2013.

[13]范春桥，张重远，李文博，等.干式变压器温度场的仿真计算与分析[J].技术应用，2012，25（3）：76-79.

[14]李岩，刘永志，井永腾.隔爆干式变压器温度场有限元分析[J].电力系统及其自动化学报，2012，24（4）：59-63.

[15]刘永志，李岩，井永腾.基于Fluent软件的电力变压器温度场计算与分析[J].高压电器，2012，48（10）：6-11.

[16]曹玉璋.传热学[M].北京：北京航空航天大学出版社，2001：2-56.

[17]NING Wang，DING Xueqian.Three-dimensional finite element analysis on fluid thermal field of dry-type transformer[C]// 2012 Second International Conference on Instrumentation& Measurement，Computer，Communication and Control，2012.

[18]路长柏，郭振岩，刘文里，等.干式电力变压器理论与计算[M].沈阳：辽宁科学技术出版社，2003.

Simulation of three-dimensional temperature field of cast-resin dry-type transformers

ZHANG Mu，GAO Li-ye，WEI Juan，XIU Chun-bo
（School of Electrical Engineering and Automation，Tianjin Polytechnic University，TianJin 300387，China）

To conveniently diagnose the faults of dry-type transformer mostly due to abnormal temperature rise directly or indirectly，and the simulation of the hot-spot temperature has important theoretical and engineering application value.According to the actual structure of dry-type transformer，a three-dimensional axisymmetric heat conduction model is established，and the simulation of temperature field calculation of dry-type transformer is carried out based on Comsol Multiphysics to calculate the temperature field distribution and iron core，windings temperature rise curve.Through the comparison between the actual data and the results of the simulation analysis，the temperature distribution and the hottest spot temperature at position 2/3 from the bottom in the low voltage winding is determined.It provides a theoretical reference for dry-type transformer diagnosis and structural optimization of online design.

dry-type transformers；fluid temperature field；hot-spot temperature；finite element simulation

TM412

A

1671－024X（2015）03－0062－05

10.3969/j.issn.1671-024x.2015.03.014

2014-11-27

国家自然科学基金资助项目（61203302）；天津市基础与前沿技术研究计划（14JCYBJC18900）

张 牧（1962—），男，教授.研究方向为检测技术与自动化装置.E-mail：zhangmu@tjpu.edu.cn