轴承间距对水下结构振动与声辐射影响研究*
2015-04-18宁荣辉翁雪涛朱石坚李海峰
宁荣辉 翁雪涛 朱石坚 李海峰
(海军工程大学动力工程学院 武汉 430033)
0 引 言
水下结构的振动及声学问题是工程实际运用中的难题之一.螺旋桨作为水下结构的主要动力来源,它通过推进轴系给水下结构提供推力,而由轴系传递的推力也是影响水下结构的振动及声辐射的主要因素之一,因此研究艉轴轴承间距对水下结构振动与声辐射特性的影响,对于保证轴系的正常工作和提高水下结构声隐身性能具有重要的意义.周春良等[1]对船舶轴系的合理轴承间距进行了研究,张宏辉等[2]也对轴承的间距对船舶轴系的振动进行了研究,然而轴承间距对水下结构的声辐射的影响,还没有进行过相关的研究.而水下结构基本上都具有复杂的结构,采用解析法求解其辐射声功率及其辐射效率几乎是不可能的.因此,对于水下结构的振动及声辐射的研究一般将其简化为有限长圆柱壳体[3-4]然后对其进行理论分析,或者直接运用有限元/边界元[5-6]的方法对其进行数值分析计算.本文采用有限元/边界元的方法建立了水下结构推进轴系的有限元模型以及水下结构与流体相互作用的流固耦合模型,通过声学软件Virtual Lab对该耦合模型的声辐射特性进行分析计算,研究艉轴轴承间距对水下结构振动及声辐射的影响.
1 结构振动声辐射理论
1.1 有限元/边界元理论
针对水下结构的复杂特性,有限元/边界元方法是对其声辐射分析计算的有效方法之一.在简谐激励作用下结构的运动方程如下.
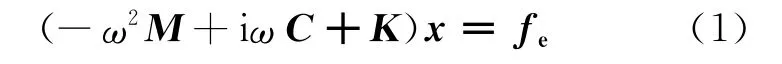
式中:M,C和K分别为结构的质量、阻尼和刚度矩阵;x为结构的节点位移向量,fe为外激励载荷向量.
结构振动在流通介质中产生的稳态辐射声压p满足Helmholtz微分方程、流固界面条件及Sommerfeld辐射条件.

式中:k=ω/c为波数;ω为圆频率;c为流体介质中的声速;ρ为流体介质的密度;n为耦合面S的外法向单位矢量;vn为外法向振速;r=|Q-P|,Q为结构表面S上任意点,P为空间中任意点.
式(1)的基本解自由场格林函数为
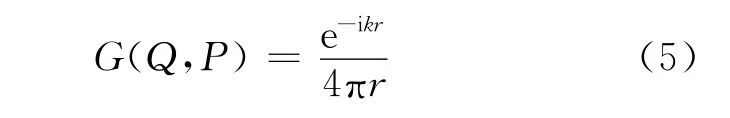
考虑边界条件,对式(1)使用加权残值法并利用格林函数,可以得到Helmholtz直接和间接边界积分方程,对边界积分方程利用边界元法进行离散,即得到边界元求解方程.
1.2 结构声辐射声功率及辐射效率计算方法
由辐射声功率和均方法向速度计算公式[7]
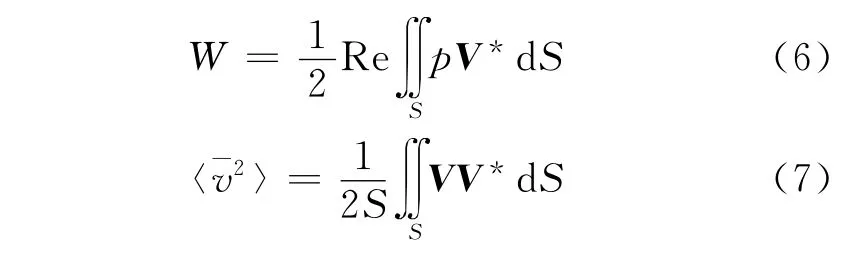
利用有限元/边界元方法计算得到的结构的速度向量,可以计算得到结构的辐射声功率以及均方法向速度,再利用声功率级和均方法向速度级的定义.
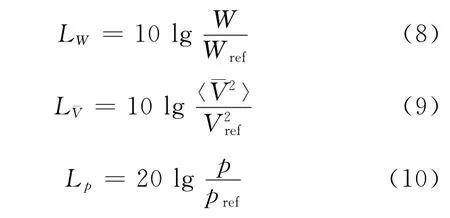
可得到结合面S上的辐射声功率级和均方法向速度级;并得到外流体域声场点的辐射声压级.式中:Wref=1×10-12W,Vref=5×10-8m/s,pref=1×10-6Pa.
最后,由模态声辐射效率计算公式

可以计算得到水下结构的声辐射效率.
2 结构有限元模型
由于尾轴轴承主要受螺旋桨横向振动的激励,因此本文的计算模型仅考虑垂直于尾轴方向上的激励.推进轴系简化模型如图1所示,将尾轴轴承简化为单点支撑,推力轴承采用一个刚度系数为3.0×106N/m的垂向弹簧和一个刚度系数为8.0×106N/m的纵向弹簧模拟支撑,尾轴前轴承采用一个刚度系数为4.0×106N/m的垂向弹簧模拟支撑,尾轴后轴承采用一个刚度系数为6.0×106N/m的垂向弹簧模拟支撑.
水下结构采用Patran软件进行有限元建模,借鉴美国研究署的SUBOFF艇理论外形[8],对壳体内部结构进行相应简化.结构包括甲板、舱壁、环肋和推进轴系等主要部分,推进轴系选取推力轴承到螺旋桨之间的一段,包括推力轴、中间轴、尾轴和螺旋桨.图2为水下结构有限元模型,图3为结构尾部有限元模型,壳体、甲板、舱壁和推力轴承座均采用壳单元,并对外壳体单元加上附连水质量;壳体结构上的肋骨、甲板和舱壁上的加强筋以及推进轴系采用梁单元;螺旋桨加上附连水的质量,采用质量点单元,作用于尾轴的末端;轴承采用弹簧单元,全轴长14m,推力轴承与尾轴后轴承的距离保持为13m,对尾轴前轴承与推力轴 承 距 离 分 别 为3.4,4,4.6,5.2,5.8,6.4,7.15m时进行分析.

图1 轴系模型图
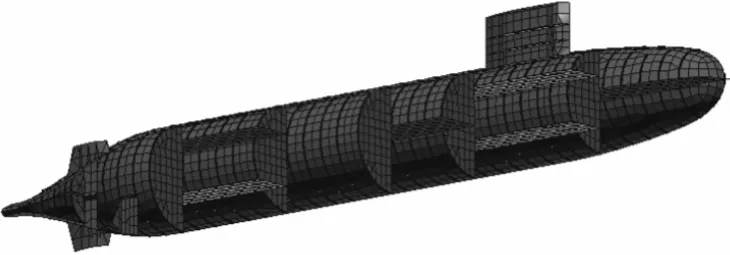
图2 水下结构有限元模型
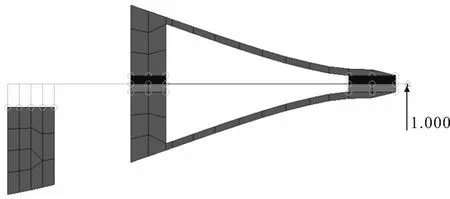
图3 结构尾部有限元模型
3 数值计算及结果分析
保持尾轴后轴承与推力轴承之间的距离不变,只改变尾轴前轴承与推力轴承之间的距离,结合第2节的原理,利用有限元方法,首先分析轴承间距对轴系固有特性的影响,然后得到水下结构外壳表面的速度响应,并将计算得到的速度响应作为结构水下声辐射的边界条件.计算时,激励力幅值为1N,垂向作用于螺旋桨处,如图3所示,计算范围为5~505Hz,步长取2Hz.
3.1 轴承间距对轴系固有特性的影响
表1是利用有限元软件计算了尾轴前轴承与推力轴承间距分别为3.4,4,4.6,5.2,5.8,6.4,7.15m时,轴系前6阶横向振动模态.
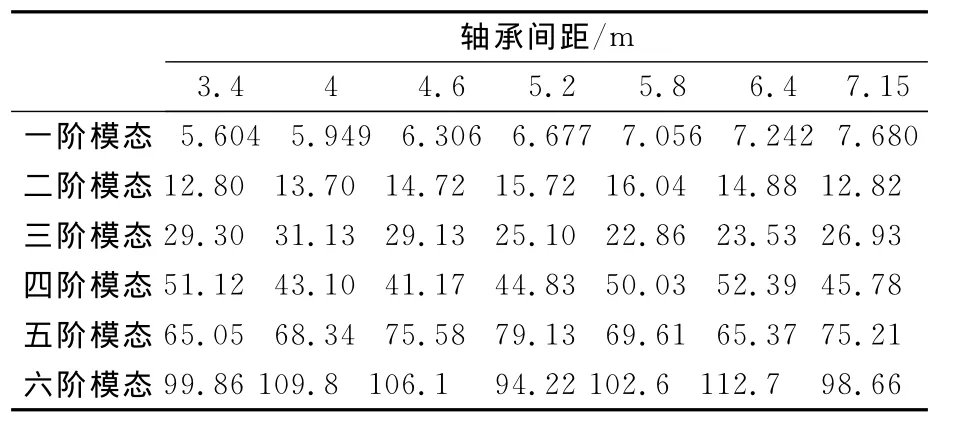
表1 不同间距下轴系前6阶横向振动模态 Hz
由表1可见,不同的轴承间距对轴系固有特性的影响不一样.随着尾轴前轴承与推力轴承之间距离的增加,轴系的第一阶横向振动模态频率也随之增大,在3.4~4.6m的轴承间距区间内,轴系的第1,2,5,6阶振动频率随着尾轴前轴承与推力轴承间距的增加而增大,第4阶振动频率随轴承间距的增加而增大;在4.6~5.8m的轴承间距区间内,轴系的第1,2,4阶振动频率随轴承间距的增加而增大,第3阶振动频率随轴承间距的增加而减小.因此,在轴系结构设计时,应综合考虑轴承间距变化对各阶模态频率的影响.
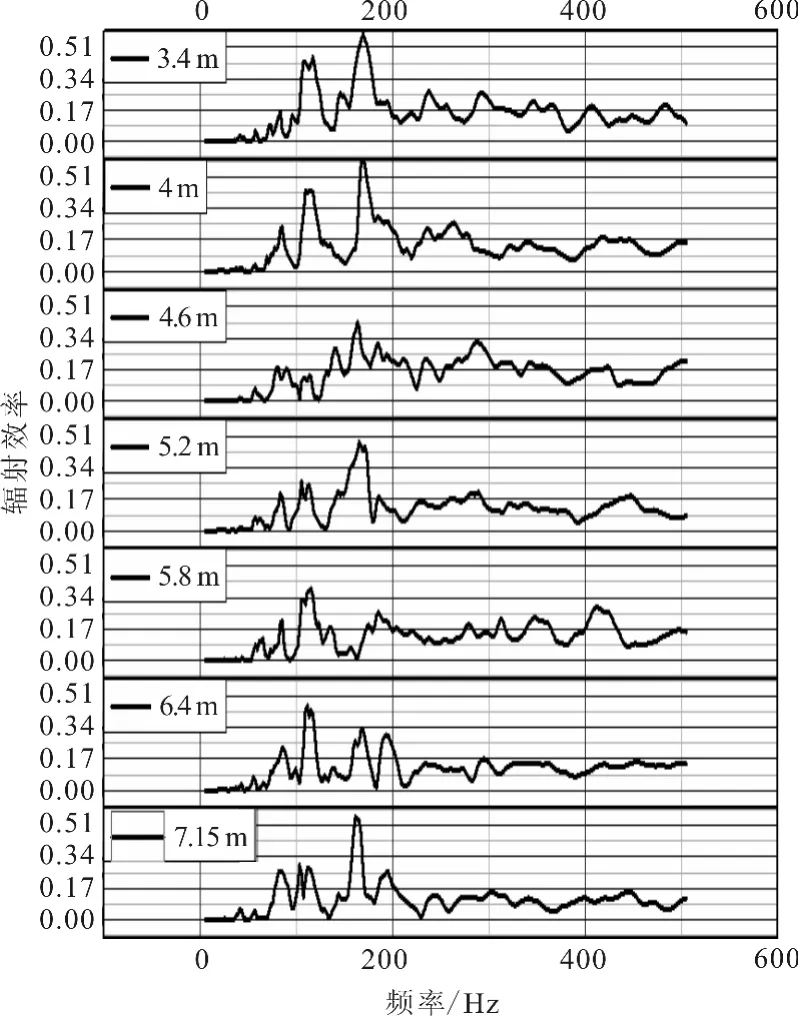
图4 声辐射效率频响曲线
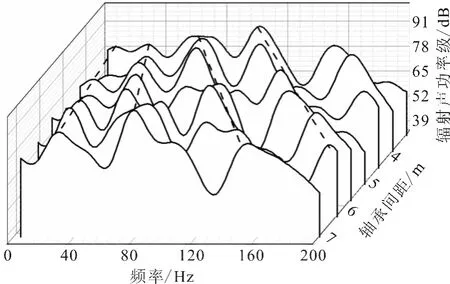
图5 辐射声功率级频响曲线
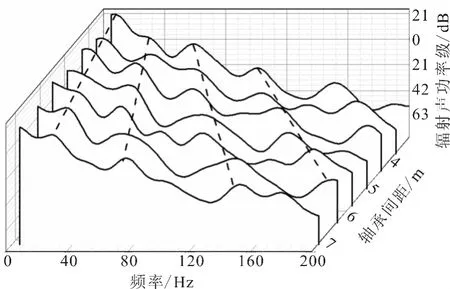
图6 均方法向速度级频响曲线
3.2 轴承间距对水下结构声振特性的影响
图4 是水下结构声辐射效率曲线图,从图中可以看到,当尾轴前轴承与推力轴承的间距变化时,在85,115,165Hz频率附近始终保持着相对较高的辐射效率,因此,在水下结构的设计过程中,要优先考虑降低这些频段处的振动.从图中还可以看到当频率高于200Hz时,各情况下的声辐射效率都相对较低,而且一般水下结构都安装有隔振器,可以较好的隔离高频振动,因此,在接下来的研究分析中本文将主要考虑200Hz以下的频率范围.
图5~7分别是在不同轴承间距情况下,水下结构辐射声功率级、均方法向速度级,以及100m处的辐射声压级随频率变化的瀑布图.从图中可以看到,随着轴承间距的增加,辐射声功率级、均方法向速度级以及100m处的辐射声压级的峰值的频率也会随之增加(如图中虚线标出的各个峰值).
由于船舶轴系低频振动突出,因此主要分析轴承间距变化对水下航行器低频段声振特性的影响.表2分别列出了在各个轴承间距下,辐射声功率级、均方法向速度级、100m处辐射声压级前3个峰值的频率值,理论上讲,由共振引起的辐射声功率级、均方法向速度级、100m处辐射声压级的共振峰应该都是在相同的频率值处出现,而表中列出的3组数据的共振频率虽然并不完全相同,不同值的频率差别都不超过2Hz.又由于分析步长是2Hz,因此这些频率值的差别应该是由计算误差造成的.为了更准确反应各个共振峰的频率值与轴承间距的关系,将3组频率值平均值作为共振峰的频率值,结果见表3,最后对轴承间距和平均峰值频率进行了线性拟合,拟合曲线及其结果如图8所示.由图8可见,当轴承间距增加时,前水下结构声辐射的前3阶峰值频率也随之增加,且峰值频率的变化与轴承间距的变化近似呈线性变化,因此在水下结构设计过程中,可以通过改变艉轴轴承的间距来避开推进轴系的工作频率,以降低水下结构的辐射噪声.
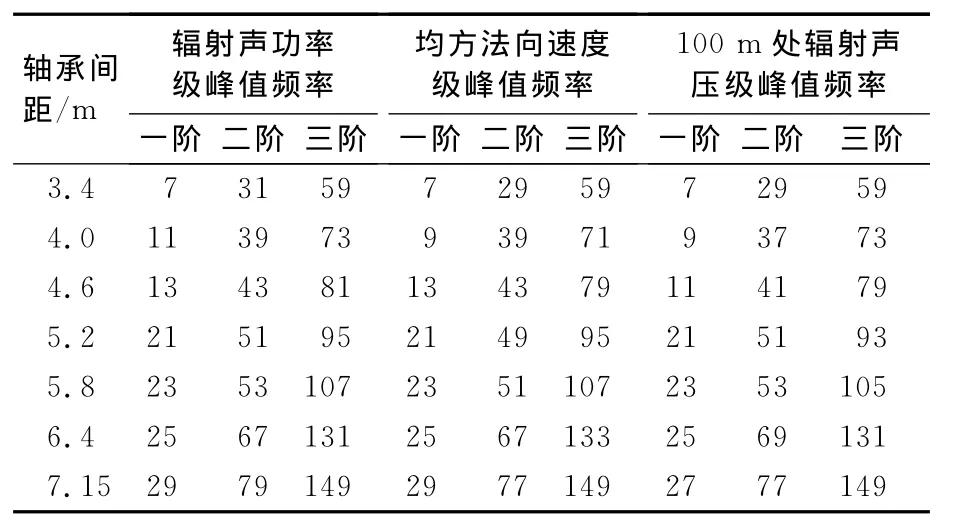
表2 不同轴承间距下峰值频率 Hz
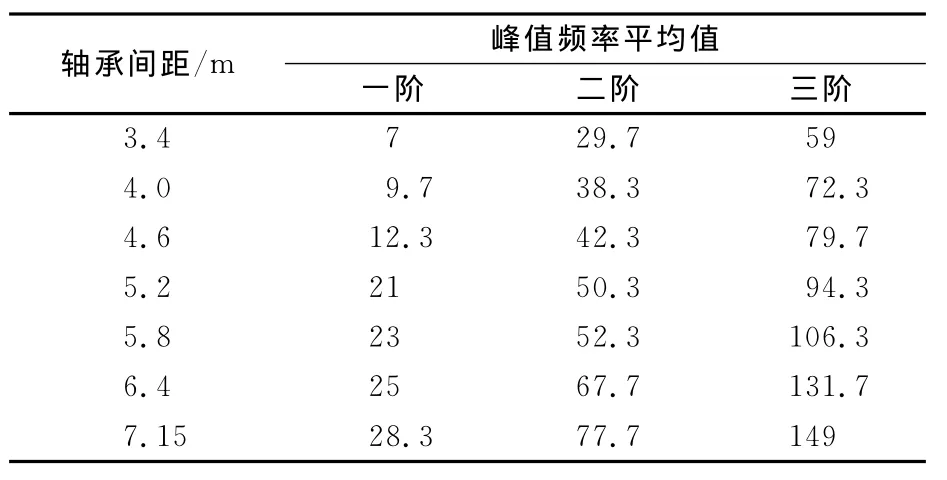
表3 平均峰值频率 Hz
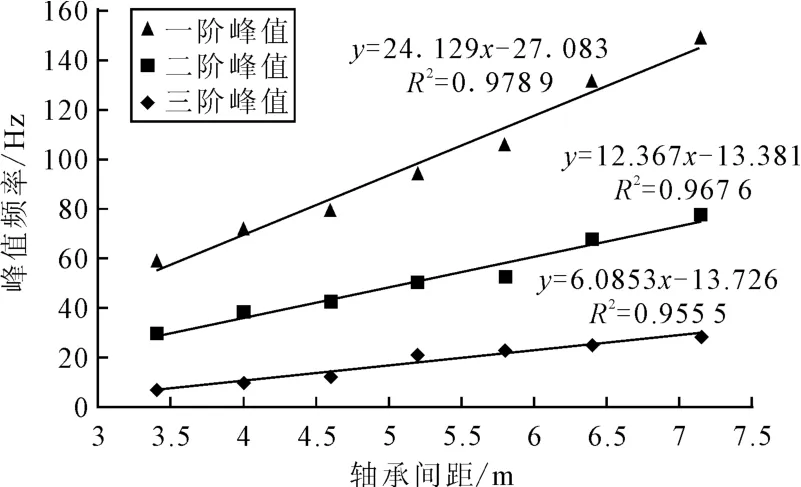
图8 轴承间距与前三阶峰值频率拟合曲线图
4 结 论
1)在一定范围内,尾轴轴承间距增加,轴系固有频率发生变化,其中一阶固有频率随着轴承间距的增加而增加.
2)随着轴承间距发生改变,水下结构的声辐射效率也会发生改变,但是并不会改变水下结构声辐射效率较高的频段范围,而且当频率高于一定频率时(对于本文的研究模型,为200Hz),轴承间距对水下结构的声辐射效率影响不大.
3)随着轴承间距的增加,水下结构的辐射声功率级、均方法向速度级和100m场点处辐射声压级都会发生改变,其前三个峰值的频率随着轴承间距的增加而增加,峰值处的频率与轴承间距的变化呈近似线性变化.
轴承间距对水下航行器的结构振动及声辐射会产生较大的影响,因此在轴系设计过程时利用有限元/边界元软件计算出轴系对结构模态的影响及其对结构振动与声辐射的影响规律,可以在轴系设计过程中避开推进轴系的工作频率,有利于降低水下结构的振动及辐射噪声.
[1]周春良,刘占生,郑洪涛.轴承支撑长度及间距对船舶轴系振动特性影响[J].船舶工程,2007,29(5):16-18.
[2]张宏辉,周继良,唐锡宽.船舶轴系的合理轴承间距的研究[J].舰船科学技术,2007,29(4):54-56.
[3]CHEN Junming,HUANG Yuying,ZENG Gewei.Vibration and acoustic radiation from orthogonally stiffened infinite circular cylindrical shells in water[J].China Ocean Engineering,2002,116(4):437-452.
[4]LIU Qingyu,FANG Shiliang,CHENG Qiang,et al.Intrinsic mode characteristic analysis and extraction in underwater cylindrical shell acoustic radiation[J].Sci China-Phys Mech Astron,2013,56(7):1339-1345.
[5]黎 胜,赵德有.用有限元/边界元方法进行结构声辐射的模态分析[J].声学学报,2001,26(2):174-179.
[6]ZHOU Q,JOSEPH P F.A numerical method for the calculation of dynamic response and acoustic radiation from an underwater structure[J].Journal of Sound and Vibration,2005,283(3/5):853-873.
[7]杜功焕,朱哲民,龚秀芬.声学基础[M].南京:南京大学出版社,2012.
[8]NANCY C G,HTHOMAS T H,MING S C.Geometrics characteristics of DARPA SUBOFF models[R].Bethesda:David Taylor Research Center,1989.
