仿生智能算法群桥水域航路规划应用研究＊

杨 柯 徐言民 高如江 金 城 陈 敏

（武汉理工大学航运学院1） 内河航运技术湖北省重点实验室2） 武汉 430063）

0 引 言

仿生智能计算是人工智能领域的一个新兴的重要分支，近年来，仿生智能计算无论是在理论还是在应用方面均取得了很多突破性的进展，极大的促进了相关领域研究发展.仿生智能计算是一种模拟自然界生物“优胜劣汰”思想的算法，算法本身具有自适应、自组织和自学习特点，能够解决传统计算中难以解决的非线性复杂问题.人工智能算法由于其优越性，逐渐被引入航路规划研究领域.粒子群、蚁群等智能算法在无人机、机器人、导弹航路规划问题中表现出了极大的优越性，引起了研究人员的广泛关注.本文在介绍粒子群、人工蜂群、人工鱼群算法的基础上，分别运用以上3种仿生智能算法对群桥水域航路规划问题进行了求解，并对结果进行了对比.

1 仿生智能算法简介

1.1 PSO算法

PSO算法是由Eberhart博士和Kennedy博士于1995年提出的一种可以实现全局优化的随机优化算法.PSO算法首先随机初始化一群粒子，在每次迭代中，粒子通过跟踪个体极值点和全局最优解，从而求得全局最优值［1－2］.

1.2 ABC算法

ABC算法是由土耳其学者Karaboga提出的一种模拟蜜蜂群体寻找优良蜜源的仿生智能计算方法.ABC算法解的进化由觅食蜂、观察蜂和侦查蜂3种蜜蜂共同完成［3－4］.

1.3 人工鱼群算法

AFSA算法是受鱼群行为的启发，由国内李晓磊博士于2002年提出的一种基于动物行为的群体智能优化算法，其中觅食行为、聚群行为、追尾行为和随机行为与寻优命题的解决有着较密切的关系［5－6］.

2 群桥水域航路规划模型

2.1 群桥水域特征简要分析

群桥水域通常具有桥梁间距小的特点，以长江武汉段为例，到2015年，60km的江面上将拥有11座跨江大桥，其中白沙洲到天兴洲不足23 km的武汉江面上就拥有桥梁7座，平均桥梁间隔约3km，桥梁间距较小.由于桥梁跨度、结构不同，不同桥梁通航孔也可能会不在同一轴线.桥梁通常建设在航道断面相对狭窄处，可航水域受限制.群桥河段轮渡、汽渡、游船等交通流也会对船舶正常通航造成影响.同时，由于桥墩挑流作用，群桥水域水流变化较为复杂［7］.综上所述，群桥水域具有桥梁间距小、通航孔交错、水流变化显著，以及交通流复杂等特点，船舶操纵难度急剧加大，极易诱发船－桥碰撞、船－船碰撞事故.

2.2 群桥水域航路规划简化模型

根据群桥水域特征分析可知，桥梁间距小和通航孔交错是群桥水域主要特征.本文旨在探索不同改进方法的PSO算法在群桥水域航路规划问题的适应性，因此可以将群桥水域建模为一系列距离较近并且纵向间距相等的圆形多障碍物航行水域.考虑到船舶自身大小，将障碍物半径按照船舶大小向外拓展，船舶可以看成一个质点.船舶航行时需考虑燃油、障碍物等信息，航路规划的主要任务就是寻找一条从起始点（xs，ys）到目标点（xf，yf）路径最短且与障碍物无碰撞的路径.本文首先将航路规划问题转化为D维函数优化问题，见图1.

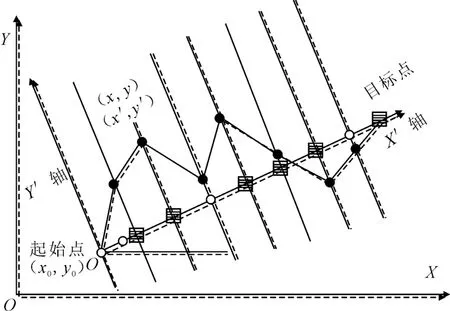
图1 坐标转换关系图

在图1中，将原坐标转换为以起始点和目标点连线为横轴的新坐标系X′OY′，θ为坐标系XOY与X′OY′的夹角.转换关系为

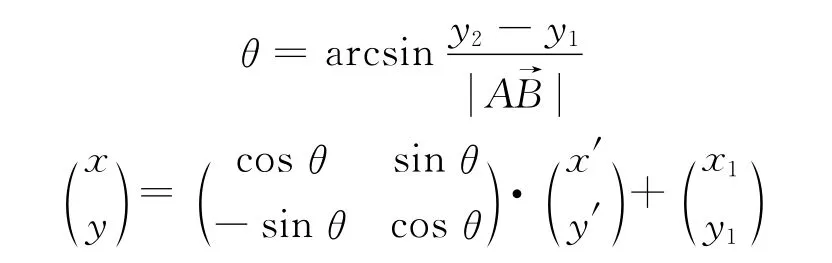
将起始点与目标点连线分为d＋1份，在每个等分点做横轴的垂线，从起始点到目标点按顺序去各垂线上任一点组成一个机器人路径序列点，用路径点纵坐标组成的向量y＝ （ys，y1，y2，…，yd，yf）即可确定一条惟一路径.同时，为了计算方便，将坐标进行量纲一的量化.

本文以路径最短和障碍物威胁最小为日指标，障碍物威胁最小可参考文献［8］所采用的威胁计算模型，故目标函数可设为

式中：J为航路跟踪代价；J1为障碍物威胁代价；J2为航路长度代价，wt为航路上各点威胁代价；wl为每条边的长度，k为不同航路代价所占得比重，本文取0.5，起始点坐标（5，15），目标点坐标（95，60）.

当船舶沿着航路Lij航行时，N个威胁源对其产生的总威胁代价为

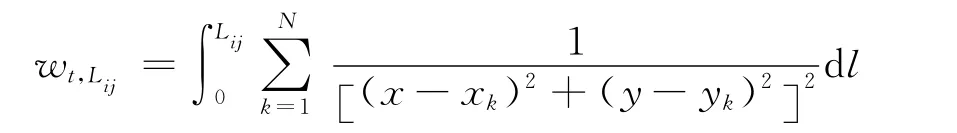
为了简化计算，把每条边分成5段，取其中的5个点来计算这条边所受到的威胁代价，见图2.若障碍物中心与该边的距离小于安全半径，则威胁代价可以按照下式计算.

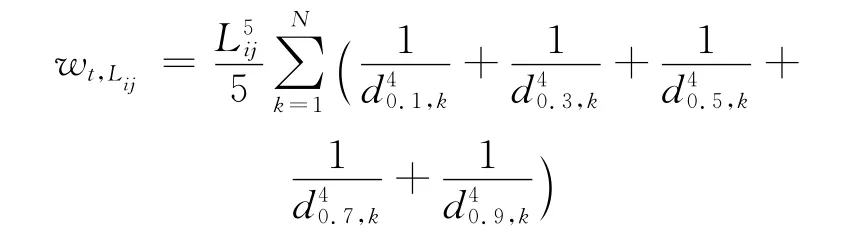
式中：Lij为连接点i，j边的长度；d0.1，k为Lij边上的1／10分点距第k个障碍物中心的距离.

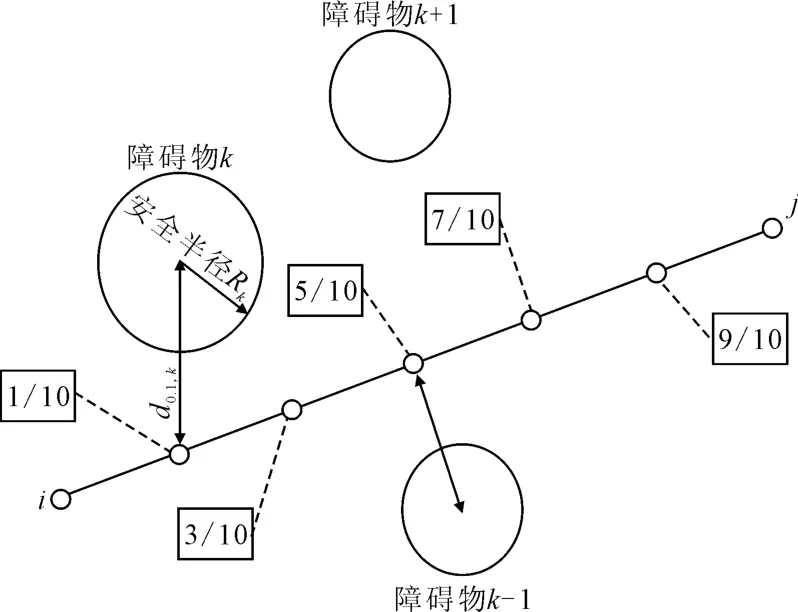
图2 障碍物威胁代价示意图

3 模型求解

3.1 PSO算法

设置PSO算法种群数量为30，粒子维数为20，迭代次数为500，对所建立的模型求解3次，选取其中最优的解，结果见图3、图4.

由图3、图4可知，标准PSO算法航路规划结果较为理想，规划航路平滑，不存在突跳点.在100代左右稳定收敛.

图3 PSO算法航路规划示意图

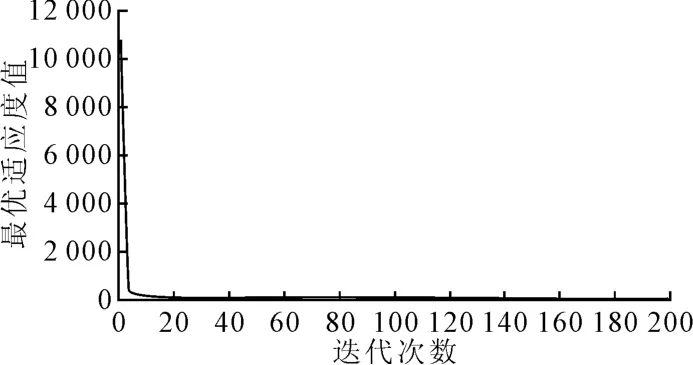
图4 标准PSO算法收敛曲线图

3.2 ABC算法

设置种群数量大小为30，维数为20，设置蜜源数量为15，侦查蜂最大探测次数设置为100，最大迭代次数为500，运行3次，取最优解，结果见图5.

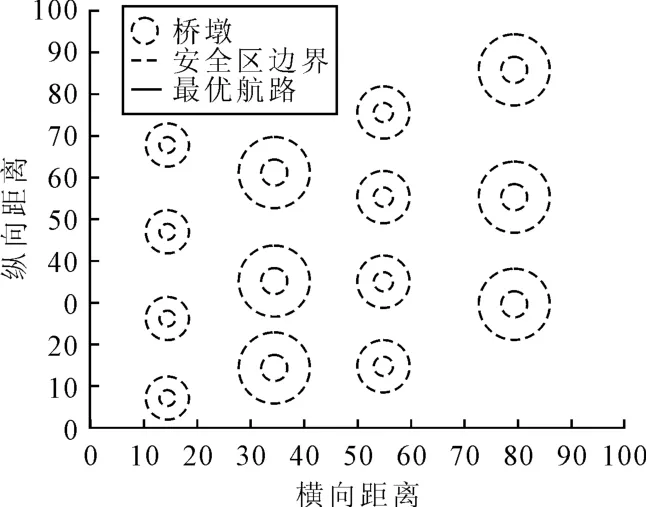
图5 ABC算法航路规划示意图

图6 ABC算法航路规划迭代曲线图

由图5和图6可知，ABC算法在求解上述模型时，也能找到最优解，但在实际迭代过程中，容易出现因陷入局部最优解而出现规划失败的现象，ABC算法310代开始收敛，400代左右稳定收敛，并且人工蜂群算法收敛速度相对较慢.

3.3 AFSA算法

目前，AFSA算法在求解多维函数极值问题方面应用还较少，但这并不影响AFSA算法具有的对初始值要求低、不需要问题的严格机理模型，甚至不需要问题的精确描述就可以求解的特点.为了探索AFSA算法的适应性，本文先对问题维数进行了简化处理，然后依次增加问题维数，对不同参数组合进行试验，最终确定了鱼群数量30、问题维数20、人工鱼个体感知半径2.5、游动步长设置0.7、拥挤度因子0.5、最大尝试次数30的参数组合，算法结果见图7、图8.

图7 AFSA算法航路规划示意图

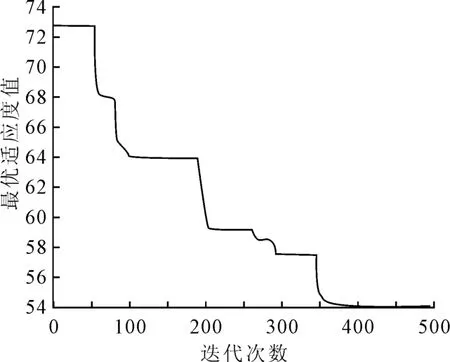
图8 AFSA算法收敛曲线图

由图7、图8可以看出，AFSA算法虽然也能找到全局最优解，但是精度不高；AFSA算法在计算本问题时，其计算速度较慢，完成500次迭代时间大约为30min，并且规划失败概率较大；算法在370代左右稳定收敛.

3.4 对比研究

仍然采取上节中各算法的参数取值，同时对3种算法分别运行3次，选取各自最优解进行对比分析，结果见图9～11.

由图9、图11可知，PSO算法在109代左右已经稳定收敛，最优适应值为三者最小，PSO算法无论是在最优适应度值还是在收敛速度方面，其表现都是三者中最优的；ABC算法最优适应度值较AFSA算法略好，但算法在470代才稳定收敛，收敛速度明显不如PSO算法；AFSA算法在求解成功率方面明显低于其他2种算法，计算耗时较长，参数较多，参数对算法精度和收敛性影响较大.因此，为了提高算法在航路规划领域的适应性，ABC算法应该主要考虑对其收敛速度进行优化，AFSA算法应考虑对其计算速度、参数数目和寻优精度方面进行改善.

图9 智能算法航路规划对比示意图

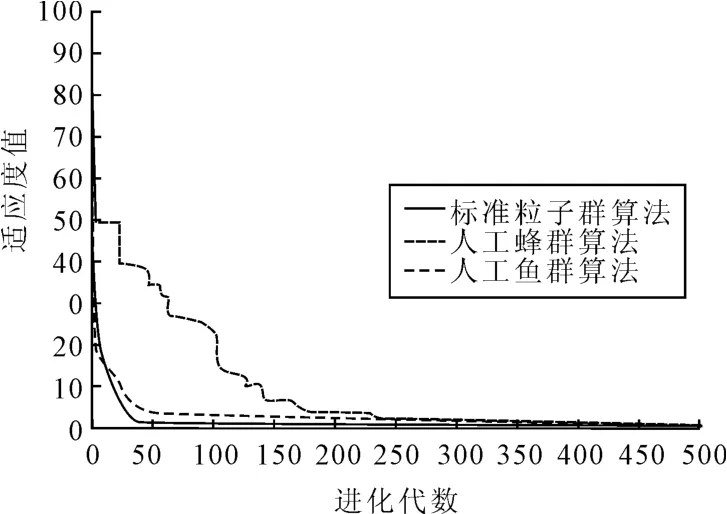
图10 智能算法最优个体适应度值对比图

图11 仿生智能算法收敛速度对比图

4 结束语

本文介绍了PSO，ABC和AFSA三种仿生智能算法，并针对群桥水域航路规划问题进行了建模研究，证明三种算法均能运用于航路规划研究；分析了三种仿生智能算法在解决该类问题时的优缺点，并明确了ABC和AFSA算法后期的优化方向，为群桥水域航路规划研究提供了新的研究方法.

［1］SCOTT H J.Improving particle swarm optimization path planning through inclusion of flight mechanics［D］.Iowa：Iowa State University，2010.

［2］刘慧卓，杨金孝，王泰然，等.改进粒子群算法在三维航路规划中的应用［J］.火力与指挥控制，2013（11）：141－143.

［3］杨小东，刘 波.人工蜂群算法加速收敛技术研究［J］.计算机技术与发展，2014（4）：25－28.

［4］GORKEMLI K D，CELAL B O.A comprehensive survey：artificial bee colony （ABC）algorithm and applications［J］.Artificial Intelligence Review，2014（8）：21－57.

［5］王培崇，雷凤君，钱 旭.改进人工鱼群算法及其收敛性分析［J］.科学技术与工程，2013（3）：616－620.

［6］王培崇.人工鱼群算法研究综述［J］.中国民航飞行学院学报，2013（4）：22－26.

［7］罗伟林，甘浪雄，邹早建.桥墩附近流场分布及对通航船舶的影响［J］.中国航海，2014（1）：66－70.

［8］韩 超，王 赢.一种基于改进PSO的无人机航路规划方法［J］.舰船电子工程，2014（4）：49－53.