应用于铣削参数优化的粒子群和遗传交互算法

马 超，蔡 军，杨 飞，崔 彬

MA Chao,CAI Jun,YANG Fei,CUI Bin

国电南瑞科技股份有限公司，南京210061

Nari Technology Development Limited Company,Nanjing 210061,China

1 引言

粒子群算法（PSO）的基本思想是模拟鸟类的群体行为，鸟类在搜索食物过程中，首先记录每个个体在搜索食物过程找到的最好位置，称之为“局部最优”，其次记录所有成员找到的最好位置，称为“全局最优”。每一只鸟都会依据这两个变量为轨迹来搜索最佳位置。粒子群算法具有原理简单，收敛效率高，收敛精度高等优点，但前期易陷入局部最优解等缺点。遗传算法（GA）的基本思想是模拟生物遗传进化过程，是一种进化算法，采用选择、交叉和变异等遗传算子，有很强的全局搜索能力，具有简单、通用、鲁棒性强等优点，但算法效率及精度有待提高，特别是后期易陷入局部最优解。目前，智能优化算法已广泛应用在系统控制、计算机工程、人工智能和管理工程等工程领域。针对具有非线性、多极值、大规模、强约束等特点的工程问题，寻求一种适应性强，具有通用作用的智能交互算法已成为有关学科的主要研究目标和方向。

散热器基板简称散热基板，常用材料有钢、铝、铜等，常用于电力系统IGBT、GTO 等功率元件的热交换场合。功率元件的散热能力受贴装工艺、散热器和冷却方式等因素影响，而研究表明，材料的表面质量会对材料的导热性产生一定影响，比如随着表面粗糙度增大，材料的导热率下降[1]；随着表面残余应力增大，材料的导热率下降[2]。因此，散热基板的表面质量对功率元件的散热有很大影响。散热基板工艺参数主要包括：切削速度、进给量和切削深度，该三要素直接影响产品质量和企业效益。

当前对于材料加工的工艺参数优化的方法有多种，根据文献[3]所述，综合机械动力学理论和智能优化算法在工艺参数优化领域有很明显的优势，本文首先是提出一种用于求解非线性、多极值、多维度的智能优化算法，然后给出上述工艺参数优化理论应用于散热基板铣削优化的工程实例。

2 粒子群和遗传交互学习算法

在粒子群算法中，群体由个粒子构成，也即种群规模。设zi=(zi1，zi2，…，ziD)，zi为第i个粒子的D维位置矢量，根据适应度函数计算每个粒子的适应值，比较每个粒子所处位置的优劣；vi=(vi1，vi2，…，viD)为第i个粒子的飞行速度；pi=(pi1，pi2，…，piD)为单个粒子搜索的最优位置；pg=(pg1，pg2，…，pgD)为整个群体搜索的最优位置。在更换搜索位置时，粒子根据式（1）和（2）更新速度和位置：

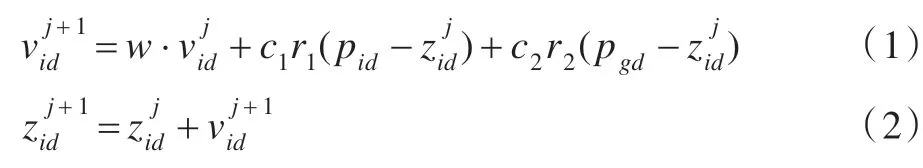
其中，w为惯性权重，j是迭代次数，r1，r2为概率随机数。式（1）第二项是粒子对自身经验学习的认识，第三项是粒子间的协作经验学习。粒子通过公式（1）、（2）来更新自身的速度和位置寻找最优解。

粒子群算法是一种基于自身学习和社会学习的智能进化算法，其优点：群体搜索并基于经验学习，具有记忆能力；通用性强，不依赖于问题信息；搜索效率高，原理简单，便于实现。当然还有一些缺点，如：粒子全局学习能力弱，容易陷入局部最优解；算法性能对参数具有一定依赖性；缺乏具体的理论指导等。针对上述缺点，不同学者都对基本PSO 算法提出改进，主要类别有：基于位置和速度更新策略[4-6]的改进；基于多种群的策略[7-8]的改进；基于拓扑策略[9-10]的改进；基于混合粒子群和其他算法[11-14]的改进；基于生物行为策略[15-17]的改进。

针对PSO 算法的不足，本文提出一种基于粒子群和遗传算法的交互学习的搜索算法，算法属于所述混合策略中的一种。综合遗传算法和粒子群算，并采用交互学习的搜索策略，在搜索最优解过程中避免算法过早陷入局部极值点，从而获得全局最优解，命名为Integrated PSO and GA，简称“IPGA”。

2.1 基本思想

PSO 和GA 都属于搜索算法，PSO 侧重于比较过程搜索，GA 侧重于自然寻优搜索，因此，PSO 在搜索时间上有优势，而GA 在搜索解上有优势，因此，本文提出一种采用PSO 和GA 的混合搜索架构，利用各自优势进行寻优的混合算法思想。在粒子搜索最优位置过程中，同时探索是否有更好的位置，这一随机探索过程将大大增加优良粒子的机会，并获取较优的解。从原理可以看出，PSO 和GA 进行共同进化、寻优和相互学习，基本示意图可看图1。

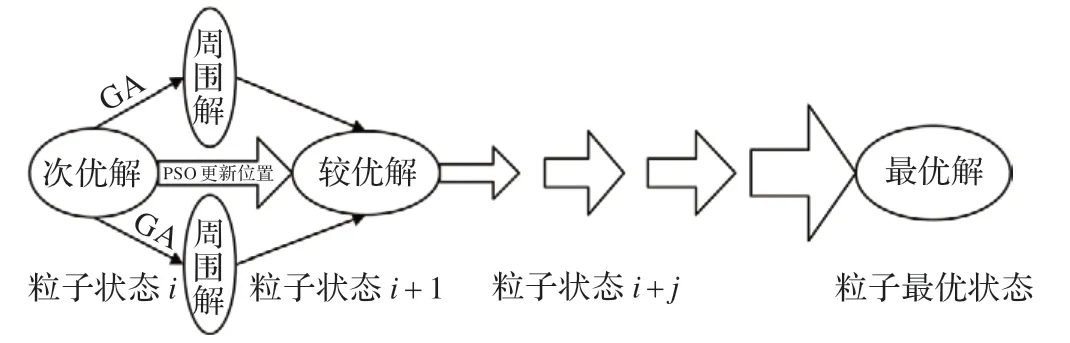
图1 PSO 算法基本思想

2.2 IPGA 参数分析

为了满足算法的动态搜索性，PSO 中的参数如w，c1，c2等要具有一定的动态特性以满足种群特性，本文采用动态递减非线性惯性权重[18]，即：

式（3）中，k，wmax，wmin，j，jmax分别是控制因子，最大权重值，最小权重值，当前迭代次数，最大迭代次数。本文采用非对称线性变化学习因子策略：

式中，c1s，c2s表示c1和c2的迭代初值，c1e，c2e表示c1和c2的迭代终值。

算法中采用的遗传算子有选择、交叉和变异。为了使粒子在搜索过程中找到更多的优良粒子，并且不过分破坏已获取较优粒子的优良性，故在采用遗传算子过程中，采用以下两种措施：

（1）使用顺序选择的方法[19]，设置给粒子的选择概率，并且把最好的粒子赋予最大的选择概率，这样一定概率选择的父代和随机选择的母代经过交叉变异[20]后将产生一定的随机粒子（式（6）），便于得到较优良的粒子。

式（6）（7）中，p表示（0，1）间的随机数。

（2）粒子群体的聚集程度进行分析[21]，当粒子的聚集达到一定程度时，采用高斯变异措施使粒子强制分散。设个体i的适应度为Fi，当前种群的平均适应度为Favg，适应度方差σ2：

式（8）中N为种群总数，F为归一化因子，限制σ2的大小，F由式（9）获得：

σ值小于一定值时，认为算法进入后期搜索，将容易出现早熟收敛现象，可以采用式（10）进行变异处理：

式（10）中，pb(i)为第i个粒子目前为止的最好位置，μ是服从（0，1）正态分布的随机向量。当种群的适应度方差小于给定的集聚阀值C时，说明粒子过于聚集，为了避免变异对粒子解的优良性产生破坏，对部分粒子采用高斯变异。粒子变异概率为q。实验发现当C，q的取值分别在（5，10）和（0.2，0.4）范围内算法表现较好。

2.3 IPGA 算法流程图及过程分析

通过对上述讲解，下面给出本文算法的流程图和实现步骤。

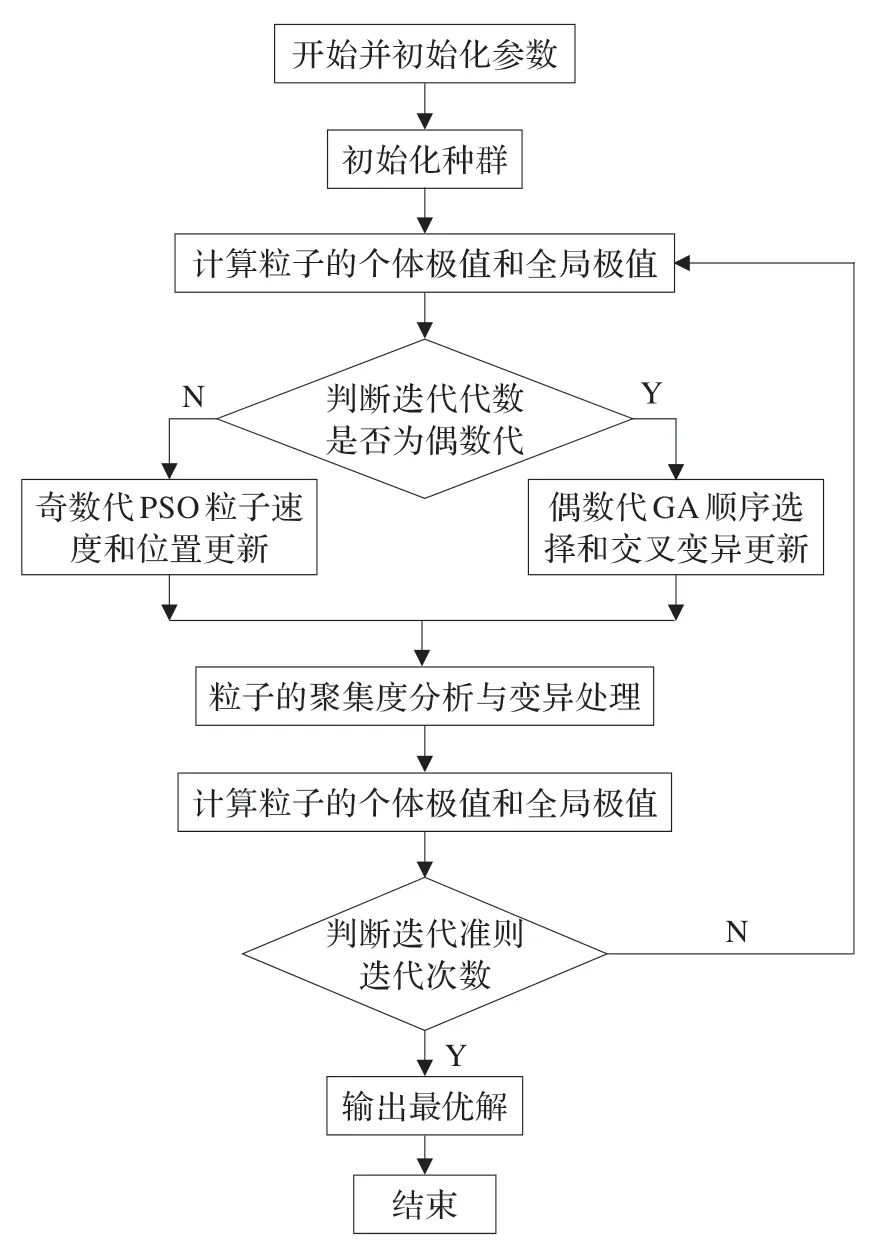
图2 IPGA 算法流程图

IPGA 算法实现步骤：

步骤1确定算法中的参数值，如变异概率、种群规模、惯性权重、学习因子、粒子维度和选择概率等。

步骤2根据初始搜索区间，随机初始化粒子速度和位置。

步骤3计算粒子的适应度值，并确定最优粒子的个体极值Pb和全局极值Pg。

步骤4增加粒子迭代次数，并判别迭代代数是偶数还是奇数。

步骤4.1偶数代时把粒子用遗传算子进行位置和速度更新。

步骤4.2奇数代时用粒子群进行速度和位置的更新。

步骤5计算粒子的聚集层度，对一定数量的粒子采用变异处理。

步骤6再次判别评价函数，确定粒子的个体和全局极值。

步骤7判定迭代次数是否满足要求，是则转向步骤8，否则转向步骤4。

步骤8输出最优粒子的全局最优位置和最优解。

3 数值实验与分析

为了体现本文算法在优化问题方面的求解性能，选取了一些常用的优化函数[20]进行对比测试。针对10维函数，采用的测试函数有：f1～f15（依次表示Sphere、Schwefel2.22、Schwefel1.2、Schwefel2.21、Rosenbrock、Rastrigin、Ackley、Griewank、Branin、GoldPrice、Hartman1、Hartman2、Shekel-Fam1、ShekelFam2、ShekelFam3、Schwefel2.26，下文用函数序号代表函数名称）。对比分析中，f1～f8的数据来源参考文献[21]；f9～f15的数据来源参考文献[22]。本次对比过程中算法采用的参数：

最大迭代次数：jmax=1 000；种群大小：N=40；权重w的最大最小值是：c1和c2的开始和终止值分别是（2，1）和（1.5，2.75）；0.9 和0.4；控制因子k取3.0；变异阀值和变异概率C，pm取值10 和0.25；运行次数30 次。

3.1 收敛精度和算法执行能力分析

基于考虑数据来源于不同参考文献，分析方法有所差别，因此表1 采用求出平均最优值结果的对比分析方法；表2 采用独立运行100 次，求出其成功运行的次数和误差[23]分析方法，本文表中黑正体表示较优解。

表1 不同算法结果性能对比分析（10 维）

表1 中Vave表示多次测试后，算法获取偏离最优解的平均误差，表2 中Psuc表示成功收敛的次数，从表1 的平均函数值以及表2 的成功搜索率和与最优值偏差可分析得知，IPGA 算法对各测试函数表现出较优的精度。采用的测试函数中f1～f5是单峰函数。f1可以测试算法的寻优精度，f5用来测试算法的执行能力；f6～f8是高维多峰函数，可以测试算法对复杂问题的求解能力；f9～f15低维多峰函数，用来检验算法的适应性。经过对比分析，IPGA 在多种复杂度问题有很高的计算精度和普遍适用性。

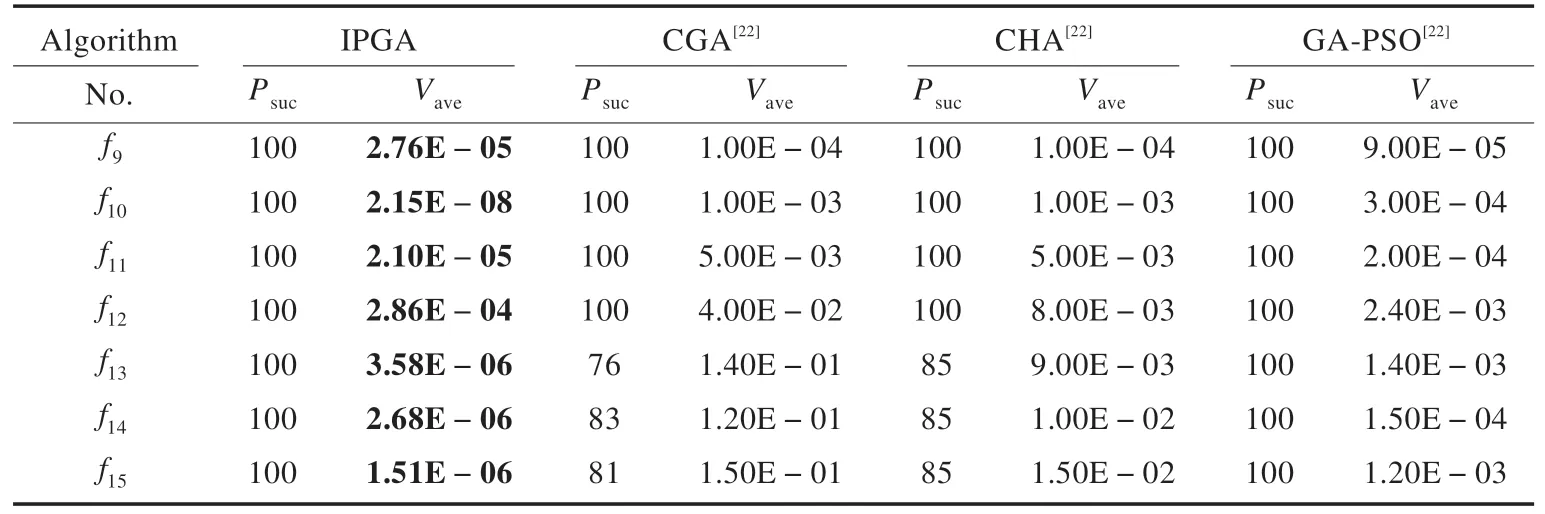
表2 不同算法结果性能对比分析

表3 10 维度问题的数值实验结果

表4 30 维度问题的数值实验结果

根据不同测试函数具有的功能，采用f5～f8来检测IPGA 对于复杂问题的求解能力，并与不同算法进行对比分析。引用文献[24-27]的实验结果进行对比分析，采用误差平均值和标准方差（独立运行30 次）的大小进行评定。上述函数实验结果具体见表3 和表4，可以看出在10 维和30 维的测试函数上，IPGA 都表现出广泛的适应性和求解能力。

3.2 算法收敛速度分析

为进一步说明IPGA 在收敛效率方面的优越性。本文结合仿真图表给出IPGA 与本文所引用比较有优势的AMQPSO 和DE/BBO 算法在求解高维复杂函数f6和f8（30 维）过程中搜索对比图。

由图3 和图4 可知，IPGA 算法在处理高维多局部最优点问题时依然具有很高的搜索效率，前30 次迭代就表现出很强的收敛性，IPGA 普遍迭代100～250 次就可以找到最终的收敛位置。在IPGA 的速度和效率方面，设置j=300，采用平均成功运行时间At的评价方法，并根据文献的数据[31]对f9～f15进行收敛效率上的对比。由于文献[22]中的GA-PSO 较CGA 和CHA 在精度和收敛性方面好，下面仅对GA-PSO 作对比，对比效果见表5。可知，IPGA 在收敛效率上占有很大优势。

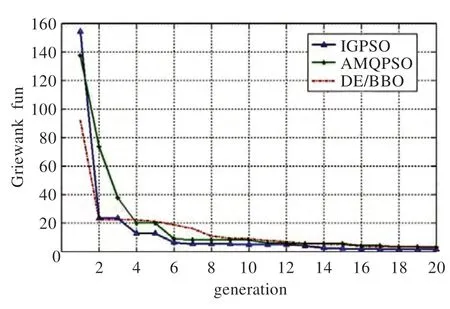
图3 f6 函数（Griewank30 维）收敛图

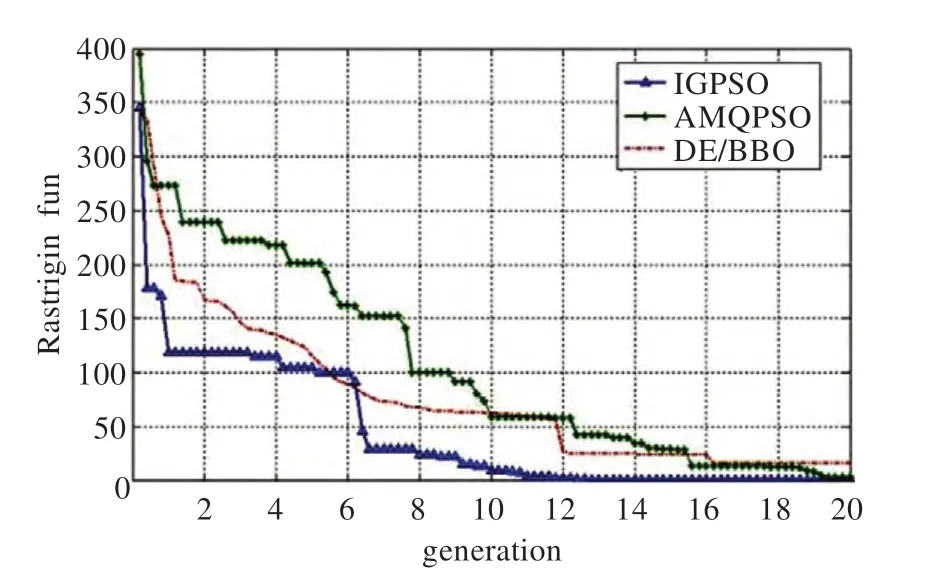
图4 f8 函数（Rastrigin30 维）收敛图

表5 算法收敛时间

4 建立铣削参数优化模型

铣削用量三要素是指铣削速度、进给量、切削深度，散热基板铣削参数即优化模型设计变量是：铣削速度v、每齿进给量fz和铣削深度ap。散热基板的加工是以降低加工工时tw[28]和加工成本Cp[29]，以提高加工质量Ra[30]和加工稳定性St[31]为优化目标，同时要满足机床的功率Pmax、铣削进给力FHmax和铣削扭矩Mmax约束，以及铣削加工过程中刀具所能承受的最大铣削速度v、每齿进给量fz和铣削深度ap等约束条件。其中：

式（12）中参数见文献[29]，加工质量是机床加工精度的重要评价指标之一，工程上采用轮廓算术平均偏差Ra作为加工表面粗糙度的重要衡量指标[32]。根据文献[32]的机械动力学理论，把铣削加工过程简化为单自由振动过程，利用振动力学理论，有如下数学模型：

式（13）中，x(t)为铣削刀刃与工件之间在铣削表面法线方向上的相对运动轨迹，此运动轨迹形成了散热基板的表面轮廓。式（13）中需要实验来获取铣削机床的特性参数：固有频率wn，刚度系数k，阻尼比ξ，铣削特性ks。

切削稳定性分析预测目的是提高材料去除率和获得高的加工质量。切削过程越稳定，表面质量一般越好，在稳定铣削的前提下，材料去除率越高越好，即转速n=1 000v/πd0与对应的稳定切削轴向深度极限值aplim的乘积越大越好。用不同加工过程中的最大主轴转速附近区域是否处在稳定区以及稳定区域最大即St的大小来评价机床切削过程的稳定性[31]。

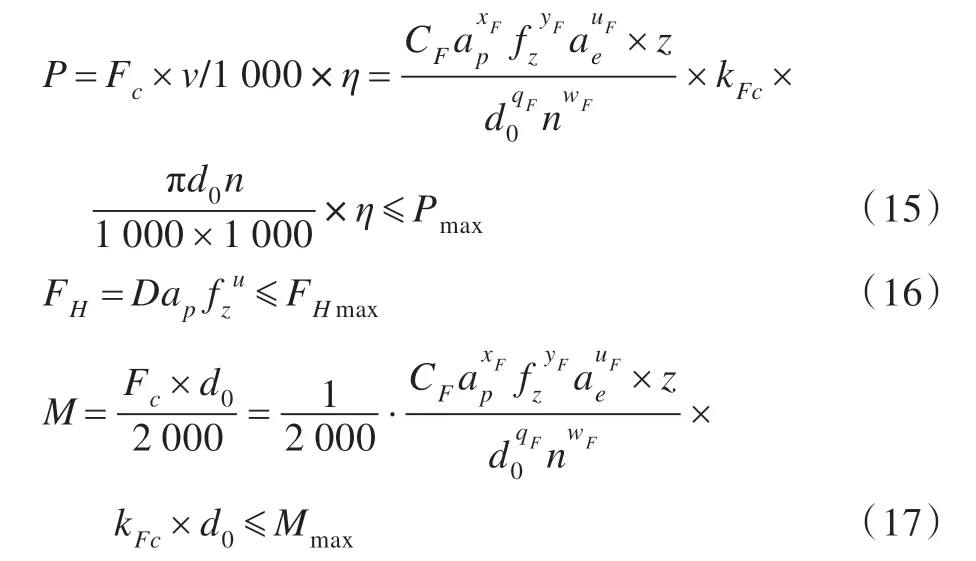
式（11）至式（17）中，参数含义见文献[28，31-32]及手册[33]。相关参数可以通过实验、手册及生产经验获得。

m=0.15，pv=0.1，uv=0.5，yv=0.4，xv=0.1,qv=0.2，Cv=25Kv=1.0

CF=30,xF=1.0,yF=0.65,uF=0.83,wF=0,qF=0.83,

kFc=0.4，d0=315 mm，Z=10，Ct=3 000元，tot=2 min，tct=2 min，Hc=5 元/min，D=349.98，μ=0.423，

wn=447，k=1.1×108，ξ=0.027，ks=2331 N/mm2，L=273 mm

在粒子群和遗传相互学习算法中，每一个进化个体z=(v，fz，ap) 的 搜 索 范 围：160 m/min ≤v≤300 m/min，0.1 mm/z≤fz≤0.28 mm/z，0 ＜ap≤4 mm。IPGA 中 的参数 设 置：N=20，j=100，0.9 ≥w≥0.4，2.5 ≥c1≥1.0，1.5 ≤c2≤2.75，p=0.5，q=0.25，C=5。

根据优化模型中的需要，本实例中采用个体粒子与最优粒子之间的间距作为目标评价函数：

式（21）中，tw0、Cp0、Ra0、St0分别表示加工工时、加工成本、表面质量、加工稳定性各自最优时的目标函数值。w1、w2、w3、w4 表示每一目标函数的权重值。优化结果见表6，表中单目标优化是只考虑单个目标函数时的优化结果，多目标优化是同时考虑每一个优化目标函数的结果，散热基板表面要有很高的加工质量，所以表面粗糙度和加工稳定性在多目标优化中应占有相当重的权重，表6 中只列出一种符合散热基板加工的组合优化结果。

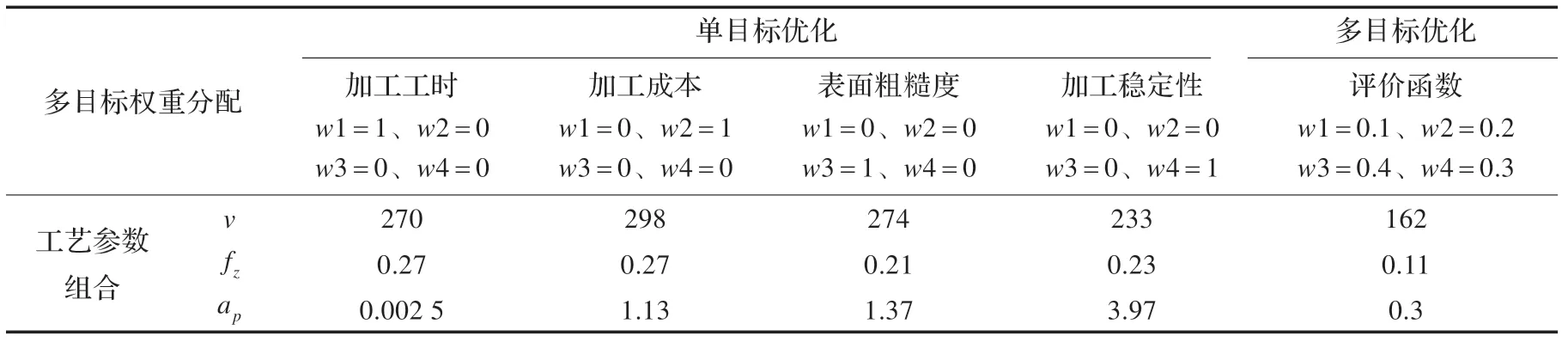
表6 IPGA 算法求解铣削工艺参数优化模型的结果

5 结语

本文从不同方面来阐述IPGA 算法的计算精度、执行能力和效率。实验证明，在IPGA 中通过引入遗传算子，并通过交叉搜索交互学习的方法使粒子尽快搜索到最优解的思路是正确的，该算法在克服粒子群算法易陷入局部最优和遗传算法收敛精度不高的缺点方面有明显优越性。比较适用于简单问题的精度求解和复杂问题的普遍适用能力方面具有优势。在工程应用中，一般并不知道问题的复杂度，而采用IPGA 这样在适用性较强的算法，求解工程问题是有优势的，通过实例也证明了算法在散热基板铣削工艺参数优化中的成功应用。

[1] 梁新刚，岳宝.微尺度下壁面粗糙度对面向导热影响研究[J].工程热力学报，2006，27（3）：475-477.

[2] 陈德欣，王志法，姜国圣，等.残余应力对、矾Cu 复合材料导热性能的影响[J].稀有金属材料与工程，2005，34（12）：1982-1984.

[3] 马超.基于加工动力学模型的工艺参数优化研究[D].华中科技大学，2012：3-7.

[4] Clerc M，Kennedy J.The particle swarm：explosion，stability，and convergence in multidimensional complex space[J].IEEE Trans on Evolut Comput，2002，6：58-73.

[5] Ratnaweera A，Halgamuge S K，Watson H C.Self-organizing hierarchical particle swarm optimizer.with time-varying acceleration coefficients[J].IEEE Trans on Evolut Comput，2004，8：240-255.

[6] Monson C K，Seppi K D.The Salman swarm-A new approach to particle motion in swarm optimization[J].Lecture Notes in Computer Science，2004，3102：140-150.

[7] Pulido G T，Coello C A C.Using clustering techniques to improve the performance of a multi-objective particle swarm optimizer[C]//Proc of the GECCO，2004：225-237.

[8] Van den Bergh F，Engelbrecht A P.A cooperative approach to particle swarm optimization[J].IEEE Trans on Evolut Comput，2004，8：225-239.

[9] Kennedy J，Mendes R.Population structure and particle swarm performance[C]//Proc of the IEEE CEC，2002：1671-1676.

[10] 王雪飞，王芳，邱玉辉.一种具有动态拓扑结构的粒子群算法研究[J].计算机科学，2007，34（3）：205-207.

[11] Li L L，Liu Wang L.An effective hybrid PSOSA strategy for optimization its application to parameter estimation[J].Applied Mathematics and Computation，2006，179（1）：135-146.

[12] Juang C F，Liu Y C.TSK-type recurrent fuzzy network design by the hybrid of genetic algorithm and particle swarm optimization[J].IEEE Transactions on Systems Man，and Cubernetics，2004，34（2）：997-1006.

[13] 高鹰，谢胜利.免疫粒子群优化算法[J].计算机工程与应用，2004，40（6）：4-6.

[14] Zhang J，Zhang J R，Li K.A sequential niching technique for particle swarm optimization[J].Lecture Notes in Computer Science，2005，3644：390-399.

[15] Krink T，Lovbjerg M.The life cycle model：Combining particle swarm optimization，genetic algorithms and hill climbers[J].Lecture Notes in Computer Volume，2002，2439：621-630.

[16] Silva A，Neves A，Costa E.An empirical comparison of particle swarm and predator prey optimization[J].Lecture Notes in Artificial Intelligence，2002，2464：103-110.

[17] 王俊伟.粒子群优化算法的改进与应用[D].沈阳：东北大学，2006.

[18] 李丽，牛奔.粒子群优化算法[M].北京：冶金工业出版社，2009.

[19] 龚纯，王正林.精通Matlab 最优化计算[M].北京：电子工业出版社，2009：315-320.

[20] 纪震，廖惠连，吴青华.粒子群算法及应用[M].北京：科学出版社，2009：59-60，72-107.

[21] 刘俊芳.基于粒子群优化和差分进化的智能算法研究[D].银川：宁夏大学，2010.

[22] Kao Yi-Tung，Zahara E.A hybrid genetic algorithm and particle swarm optimization for multimodal functions[J].Applied Soft Computing 2008：849-857.

[23] Suganthan P N，Hansen N，Liang J J，et al.Problem definitions and evaluation criteria for the CEC2005 special session on real-parameter optimization[EB/OL].（2005）.http：//www.ntu.edu.sg/home/EPNSugan.

[24] Liang J J，Qin A K.Comprehensive learning particle swarm optimizer for global optimization of multimodal functions[J].IEEE Transactions on Evolutionary Computation，2006，3：281-295.

[25] 刘波.粒子群优化算法及其工程应用[M].北京：电子工业出版社，2010：115-128.

[26] Noman N，Iba H.Accelerating differential evolution using an adaptive local search[J].IEEE Transactions on Evolutionary Computation，2008，12（1）：107-125.

[27] Gong Wenyin，Cai Zhihua，Ling Charles X.DE/BBO：a hybrid differential evolution with biogeography-based optimization for global numerical optimization[J].Soft Computing，2010，15（4）.

[28] 杨勇，沈秀良，邵华.基于遗传算法的铣削参数优化[J].机械设计与研究，2001，17（2）：60-62.

[29] 李彬，陈五一.面向切削数据进化的优化技术[J].新技术新工艺，2009（1）：20-23.

[30] 吴军.基于性能参数的数控装备服役可靠性评估方法[D].武汉：华中科技大学，2008.

[31] 吴化勇.高速切削系统动态特性研究[D].济南：山东大学，2005.

[32] 师汉民.金属切削理论及其应用新探[M].武汉：华中科技大学出版社，2003：235-331.

[33] 艾兴，肖诗纲.切削用量手册：修订本[M].北京：机械工业出版社，1985：81-111.