基于混合策略博弈视角下大学生逃课现象研究

蔡聪裕

(福建省闽江学院中文系，福建 福州350108)

一 混合策略博弈与情景假设

(一)混合策略博弈的定义

博弈最简单的理解就是在下棋时，下棋双方如何去决策，不仅要考虑自身决策对对方的影响，还要考虑对方决策对自身的反应和构成的影响。而在博弈G = {S1，．．． Sn;u1，．．． un}中，博弈方i的策略空间Si = {S1，．．． Sik}，博弈方i 以概率分布Pi= (Pi1．．． Pik)随机在其K 个可选对策略中选择的“策略”，称为“混合策略博弈”，其中0≤Pij≤1 对j =1．．． K 都成立，且Pi1+．．． +Pik=1。［1］简而言之，混合策略博弈是博弈方以一定的概率在可供选择的策略中随机选择的策略。其实，纯策略也可以看作混合策略，即选择相应纯策略的概率为1，选择其余纯策略的概率为0 的混合策略，纯策略的博弈方确定性地选择某个策略。

(二)情景假设

要研究大学生逃课现象中的博弈，必须从博弈方着手。从表面上看，博弈方似乎是教师与多名学生。其实不然，这个可以从一个情境假设得到验证。某个大学教师给101 个学生上课，在第一次课堂上要求101 个学生必须保证每一次课的到课率，如果一次的点名发现有学生逃课，逃课的同学每次逃课扣除平时分10 分，其他100 个同学扣掉1 分，期末按照百分比折合算入期末成绩。从这个情景可以看出:教师可以选择“点名”或者“不点名”，学生可选择“逃课”或者“不逃课”，教师对学生的处罚方式是扣除平时分，并且一个学生的逃课将影响到全班其他同学的平时分。假设其中任意一个学生为X，其他100 名学生为Y，那么X，Y 形成了完全信息静态博弈。如果全班学生都选择不逃课，那么他们每个学生将因为上课获取到知识而得到A 单位的效用收获，但同时付出了A 单位的时间和精力。上课本是学生的职责所在，所以收益成本相减为0。如果X 学生选择逃课而其他学生Y 选择上课，其他人要受到X 的牵连，不仅要支付A单位的时间和精力，还要受到处罚－B。其他同学都逃课，X 学生不逃课，则双方的得益正好相反。而如果所有学生都逃课，那么每个人都将得到负效用－B。根据上述的假设，X，Y 都有逃课和不逃课两种策略。双方得益矩阵则如以下图1 所显示:

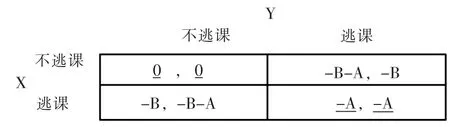
图1 学生之间的博弈

用划线法很容易得到，该博弈双方有两个能接受的、具有稳定性的纯策略纳什均衡，分别是(不逃课，不逃课)、 (逃课，逃课)。而在教师不点名的情况下，可以得知学生的行动也会是一致的。既然学生的行为是一致的，那么可以把逃课现象的博弈方看作是教师和学生整体之间的两人博弈，而不是一名教师和多名学生的博弈关系。

二 混合策略博弈在大学生逃课现象研究中的运用

(一)问题描述

得知大学生逃课现象的博弈双方为教师和学生这两个整体之间的两人博弈。而教师和学生都知道双方各种策略，并同时进行决策的情况下，双方的可能得益情况。因而，教师和学生间的博弈是完全信息静态博弈。如果学生逃课时教师未点名，学生可以利用上课时间去做其他自己喜欢的事情而获得V 个单位的效用，教师因学生的逃课而达不到预期的教学效果，设由此产生负效用为－P。如果学生逃课时教师选择“点名”的策略，则学生要受到上述所说的处罚，其负效用为－B。如果学生不逃课，教师可以利用点名的时间用于教学，其正效用为S。教师上课点名是在其职责范围内，他无得失。而学生上课是学生的本职任务，不逃课时他也没有得失。

(二)博弈分析

根据上述的问题描述，教师在该博弈中有“点名”、 “不点名”两种策略选择，而学生也有“逃课”、“不逃课”两种策略选择，根据双方的可能选择，考虑双方的可能得益。可以用下列的得益矩阵来表示这个博弈中师生双方的得益:

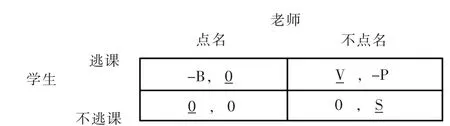
图2 教师与学生的博弈

利用划线法分析博弈双方的得益，发现该博弈双方都没有能接受的、具有稳定的纳什均衡策略组合。假设学生选择“逃课”的策略，那么教师的最佳反应是“点名”，教师点名则学生最好不要逃课，但是学生不逃课则教师选择“不点名”又符合教师的最大利益，教师不点名时学生逃课做喜欢做的事，其效用最大。因而这个博弈中没有哪个策略组合是双方可以同时接受的。因为教师“点名”与否和学生是否“逃课”之间存在的因果循环永远不会停止，因而，在一次性的博弈中无法预测博弈双方的结果，也没有纳什均衡性的策略组合。

对于这种博弈，只能确定博弈方的决策原则，以及他们的平均得益或期望。根据上述阐述，可以发现在该博弈中，博弈方的决策原则应为:不能让对方事先知道或者猜测到自己的策略，避免对方做出针对性的选择;以随机选择的方式在各种可选择的策略中进行选择，选择策略不能受个人偏好等因素的影响，使得这种选择不具有规律性;选择各种策略的概率，要使对方的策略选择无差异，不能让对方利用你的偏向获得利益。下面用图解的方法分析混合策略下，博弈双方如何确定选择各种策略的概率。

用图3 来探讨学生对选择“逃课”与“不逃课”两种策略的概率的选择。图中横轴表示学生逃课的概率，它分布在0 到1 之间，不逃课的概率为1 减去逃课的概率。纵轴表示教师不点名的期望得益。图中从S 到－P 的连线的纵坐标就是在横坐标对应的学生逃课的概率下，教师选择“不点名”的期望得益。该线与横轴交于Ps*，由于当学生逃课的概率小于Ps*时教师不点名的期望得益大于0，风险中性①风险态度分为三种类型:风险中性认为一单位期望得益与一单位确定性得益相同为风险中性;风险规避或厌恶认为一单位期望得益不如一单位确定性得益;风险寻求或偏好认为一单位期望得益好于一单位确定性得益。的教师肯定会选择“不点名”，因此在这个范围内学生可以把逃课的概率尽可能提高;当学生逃课的概率大于Ps*，教师不点名的期望得益小于0，此时风险中性的教师肯定会选择点名，学生逃课肯定被抓，因而学生必须降低逃课的概率。学生的最佳概率选择是以概率Ps*，和1— Ps*分别选择逃课和不逃课，此时教师点名和不点名的期望得益都等于0，会以一定的概率在两种策略之间随机选择，此时，选择纯策略和混合策略的期望得益都是相同的。

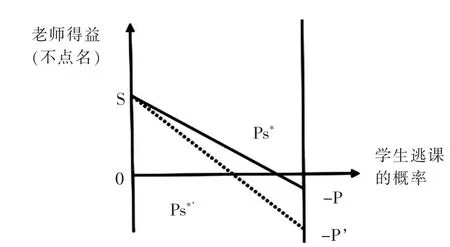
图3 学生的混合策略

为了避免让学生把握住教师策略选择的规律性，教师必须选择特定的概率分布的混合策略。与学生“逃课”与“不逃课”的概率选择相似，教师选择“不点名”和“点名”的混合策略概率分布，可以采用一样的办法来确定，图4 是教师的概率选择。结论如图所示，Pt*和1— Pt*是教师的最佳概率选择，也就是说，教师的混合策略应是以Pt*和1— Pt*的概率选择“不点名”和“点名”。

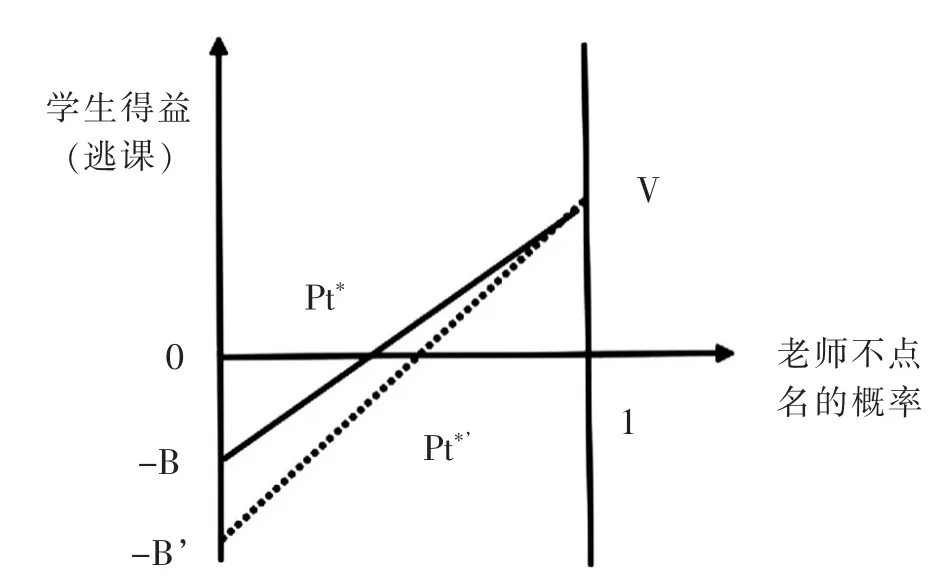
图4 教师的混合策略

在教师和学生的博弈中，当博弈双方都以上述概率分布(即最佳概率)进行随机选择时，双方都不能通过改变策略和概率，来达到改善自己的期望得益的目的，因而具有稳定性，这就是该博弈唯一的纳什均衡，即混合策略纳什均衡。

(三)价值意义

通过上述的分析，可以得知学生和教师博弈双方的混合策略。基于此，进一步分析概率分布的价值意义。如何运用混合策略博弈方法，减少大学生的逃课率。有以下两种思路值得去考虑:

第一，为了抑制逃课现象而加大对学生的惩罚会出现什么结果。对学生的逃课行为处罚加重，即是使B 增大，在图4 所示，即由－B 向下移动到－B’。如果教师的混合策略中的概率分布不变，这时学生逃课的期望得益变为负值，因而学生会停止逃课。但是从长期来看，学生减少逃课会使得教师更多地选择“不点名”，使得不点名的概率增加，从图4 的Pt*增加到Pt*’，达到新的均衡，而此时学生逃课的期望得益又恢复到0，他会重新选择混合策略。由于学生的混合策略概率分布是由图3 决定的，不受B 值的影响。因此，学校加重对学生的惩罚在长期看并不能对减少学生的逃课现象，只能在短期内抑制学生的逃课行为。

第二，如果加重教师“不点名”的负效用，会是什么结果。加重对教师不点名的负效用意味着P 增大到P’(如图3)，此时，如果学生逃课的概率不变，那么教师不点名的期望得益变为负值，在长期中，教师肯定会选择“点名”。教师点名越多，学生只能减少逃课的概率，直到Ps*下降到Ps*’，此时教师又会恢复混合策略，从而学生采取的混合策略是合理的。这说明加重教师不点名的负效用在长期中会降低逃课现象发生的概率。

三 减少大学生逃课现象的对策建议

(一)把握博弈的原则，提高课堂考勤的效果

一是课堂考勤的保密性。从上述可以知道:博弈方的原则之一是不能让对方事先知道自己的策略，一旦自己的策略被对方事先了解到，对方就会做出针对性的选择，从而不利于自身的利益。在学生和教师的博弈中，教师作为课堂考勤的主动方，为了达到课堂考勤的效果，在“点名”之前一定要注意保密性，不能让学生事先知道，否则将不能达到“杀鸡儆猴”的警示性效果。

二是课堂考勤的随机性。随机选择原则是博弈方的另一个原则，即选择策略不能有规律性，要在各种可选择策略中随机选择，若某一方的选择有规律，那么其他博弈方就会掌握他的规律，猜出其选择。因而，在课堂考勤中，教师也要把握这一博弈原则，不能在点名中形成某种规律，在某个固定的时间点经常点名，而应该随机性的进行，这样可以起到更好的效果。

(二)思想上引导逃课的学生，不可一味加大惩罚的力度

从上述博弈分析中，可以得知加大对学生逃课行为的惩罚力度，只能在短期内起到一定的效果，而且这种效果具有局限性。从长期来看，学生的逃课行为不会因为惩罚力度的加大而减少。大学生“逃课”应是大学生有目的一种主观意志和行为方式［2］。所以，要减少学生的逃课率，仅仅依靠惩罚的手段是不够的，教师必须要加强对逃课的学生思想上的引导，重视培养和激发逃课的学生学习的内在动机，激发其学习兴趣。教师可以从以下几个方面进行努力:第一、在思想方面，可以多与学生沟通，做学生的朋友，有针对性地平等地与学生交谈，了解学生的逃课的原因等实际情况，有针对地进行指导，提供帮助。第二、注意创造机会，帮助逃课的学生拥有成功的体验。多对逃课的学生进行鼓励性的评价，引导其进行积极的自我评价，增加逃课的学生的自我效能感，使得逃课的学生树立自信心和自我期望，从而增强成就动机，激发其学习的内在动机。

(三)加大教学效果的重视程度，保证学生上课的实际效果

加大对教学效果的重视程度，会促使教师不进行课堂考勤的负效用增大。因为保证学生的到课率是保证教学效果的前提，如果学生无法出勤，那么教师再精彩的课程也没有意义。所以，可以根据实际情况采取多种措施引起教师对课堂考勤的重视，如可以根据所教课程的性质等实际因素量化教师的最低点名次数，对未遵守规定的教师进行相应的惩罚，加大教师“不点名”的负效用。

当然，要加大对教学效果的重视程度，仅仅依靠课堂考勤是不够的，教师还需要从课堂教学的质量着手进行努力。比如:教师在课堂教学的过程中，要重视教学内容的实用性和价值性，引导学生对知识价值性的认知;又如，教师可加强师生间的互动，熟练掌握并交互使用讲授、演示、提问、答疑、讨论、做练习等与学生互动的教学方法。此外，教师还可以通过富有激情的授课方式、充分搜集教学相关资料、有效的课堂管理等方法来提高课堂教学的效率。

四 结束语

为了更形象地说明教师和学生的博弈，笔者进行了一定的情景假设。如某个大学教师给101 个学生上课这个情景中，提到了这样一个假设:“如果教师在一次的点名发现有学生逃课，逃课的同学每次逃课扣除平时分10 分，其他100 个同学扣掉1分，期末按照百分比折合算入期末成绩。”这个方法在实施过程中确实有一定的难度，会引起学生的强烈不满，但其揭示的本质内容是符合实际的，教师发现逃课的学生越多，肯定会加大点名的力度，这样，对未逃课的其他同学来说，逃课的成本无形中增加，会影响到他们的得益。

另外，在大学生逃课现象的对策建议中，着重从混合策略博弈这个视角对学生和教师的关系进行分析，并相应去提出建议。实际上造成大学生逃课现象的原因是多方面的，除大学生个体原因外，还包括文化影响、社会影响等客观因素。要最大限度地减少大学生的逃课现象，需要学生、教师、学校、家庭、社会等多主体进行努力，这样使学生能够充分地利用时间获取知识，提高自身素质，为步入社会做好充分的准备。

［1］向小兵． 基于博弈论中的混合策略在高校学生管理工作中的应用［J］． 中小企业管理与科技:下旬刊，2011 (8):39．

［2］陈坤华． 正途与歧途之间:普通高校大学生逃课的现实性［J］． 媒体高等教育，2013 (2):1 －5．

［3］谢识予． 经济博弈论［M］． 上海:复旦大学出版，2009:1 －9．

［4］张忠德． 大学生逃课现象的博弈分析［J］． 民办教育研究，2007 (3):67 －69．