航空瞬变电磁法对地下典型目标体的探测能力研究
2015-04-17殷长春任秀艳刘云鹤蔡晶
殷长春, 任秀艳*, 刘云鹤,2, 蔡晶
1 吉林大学地球探测科学与技术学院, 长春 130026 2 中国地质大学(武汉)地球内部多尺度成像湖北省重点实验室, 武汉 430074
航空瞬变电磁法对地下典型目标体的探测能力研究
殷长春1, 任秀艳1*, 刘云鹤1,2, 蔡晶1
1 吉林大学地球探测科学与技术学院, 长春 130026 2 中国地质大学(武汉)地球内部多尺度成像湖北省重点实验室, 武汉 430074
航空电磁法的探测能力受飞行高度、发射波形、发射磁矩和发射基频等因素的影响,致使不同分量间的勘探能力存在差异.航空电磁如对所有磁场和磁感应分量、on-和off-time数据进行观测和解释,不仅数据量大、耗时长,而且出现大量冗余数据.目前国内针对此问题尚无系统解决方法.本文针对吊舱式直升机航空电磁系统,采用积分方程法求解频率域响应,经汉克尔变换转换到时间域,计算了地下三维目标体的B和dB/dt时间域响应.利用异常体响应与背景场响应作比值,并通过设定响应阀值定义最大勘探深度,进而分析不同发射波形、不同分量以及on-和off-time期间的航空电磁系统的探测能力.基于本文分析手段,可根据实际勘探目标,确定一套探测能力较强的航空电磁最佳参数组合,为野外测量和数据处理提供技术指导,高效完成勘探任务.
航空电磁; 时间域; 探测能力; 系统设计; 磁场和磁感应; on-time和off-time
1 引言
航空电磁法(Airborne Electromagnetic简称AEM) 是一种以飞机为运载工具进行地下目标体探测的方法.它通过测量大地的二次磁场来研究地层沿水平和垂直方向的电性差异,描述地电断面的电性特征,进而了解地质构造情况(黄皓平,1991).AEM具有速度快、成本低、通行性好、可用于海域和大面积覆盖区域勘测等优势.时间域航空电磁系统用于地质填图和矿产普查已超过50年,其中大部分系统主要使用的发射波形为半正弦波,发射基频介于25 Hz和300 Hz之间,随着地质条件不同而改变.
AEM系统诞生于1948年,在20世纪70年代得到迅速发展.90年代起,时间域航电系统开始向大磁矩发射、多分量测量方向发展,并通过选择合适的脉冲频率及宽度,以期在导电地层中获得大的穿透深度.黄皓平和王维中(1990)对时间域航空电磁数据进行了反演研究,Smith和Annan (1998)分析了时间域航电系统磁场数据相对于磁感应数据的优点,Liu(1998)研究了脉冲、方波、半正弦波等几种不同发射波形对航空瞬变电磁响应的影响, 而Balch等(2003)等对三角波激励源下AeroTEM系统的on-time数据进行了反演解释.罗延钟等(2003)导出了层状大地条件下时间域航空电磁法的正演计算公式,Yin 等(2008)对半正弦和梯形波激励源下均匀半空间模型的on-和off-time电磁响应特征进行模拟和分析.陈曙东等(2012)利用自由空间回线作为目标体,推导出方波、梯形波、半正弦波和三角波的瞬变电磁响应.时间域航空电磁系统由于发射线圈和接收线圈感应的影响,理想的阶跃波形不可实现,因此,数据的处理和成像主要在off-time进行,这常常导致地面浅部信息丢失(许洋铖等,2012).半正弦波和梯形波在一定程度上可以弥补不足,对其进行全波形的分析和研究具有重要意义.裴易峰等(2014)介绍了由dB/dt数值计算磁场B的积分算法,并分析了磁场B和磁感应dB/dt对地下良导体的探测能力.
本文利用积分方程进行了三维频率域航空电磁响应的正演计算,通过汉克尔变换及高斯积分得到航空电磁三维时间域响应.然后,探讨了异常体电阻率对时间域响应的影响特征.在分析探测能力过程中,我们首先将异常响应最大值的位置设为记录点位置,并通过不断地增大异常体的埋深,使其对应的异常响应不断减小,当异常响应值到达背景(均匀半空间)响应值的10%时,定义此时的异常体埋深为最大探测深度.进而,本文针对不同发射波形、磁场和磁感应分量、on-和off-time期间的航空电磁勘探深度进行系统研究,并对不同情况下的航空电磁探测能力进行了讨论和分析.鉴于航空电磁系统对于高阻体探测能力有限的情况,本文对航空电磁系统用于高阻目标体探测能力分析不作详细讨论.本文的研究思路有益于针对不同勘探目标体设计最佳航空电磁系统参数组合,从而使得设计的仪器系统以最优的观测方式实现地下目标体探测.另外,由于我国航空电磁勘查技术目前相对落后,本文航空电磁系统探测能力研究有益于我国航空电磁技术标准和规范的制定.
2 三维时间域航空电磁系统的正演理论
本文采用的频率域三维正演算法是基于Raiche(2001)建立的.其基本思路是利用并矢格林函数理论建立二次感应场和一次场的关系,求解异常体内感应电流分布,并通过对异常体内感应电流的体积分计算航空电磁系统的频率域响应.
由麦克斯韦旋度方程出发,可得到频率域三维电磁散射问题的矢量场问题:
(1)
(2)
式中,波数k2=iωμ(σ-iωε),其中μ为磁导率,ε为介电常数,Jf代表源电流密度.
引入并矢格林函数求解磁场积分表达式,其满足的方程为
(3)
结合(1)和(3)式,得到计算任意一点电场表达式为
(4)
式中,EP(r)为入射电场,σ*和ε*分别代表目标体与围岩的电导率和介电常数之差.利用迭代方法求解(4)式可得目标体内电场,进而利用欧姆定律计算目标体内电流密度.
根据Raiche(1974)的思想,利用电磁场和并矢格林函数满足的方程,可得到磁场积分:
(5)
利用傅里叶变换将频率域航空电磁响应转换为时间域响应,即
ω.
(6)
通过简单的变量代换,我们可得到与(6)式相对应的阶跃波响应:
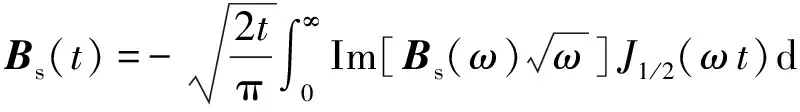
(7)
应用褶积理论和脉冲响应与阶跃响应间的导数关系,我们可得到任意发射波形时间域响应(殷长春等,2013):
(8)
(9)
式中I(t)代表发射电流,*号代表褶积.(8)和(9)式的褶积可用高斯积分进行计算(Yin 等,2008;殷长春等,2013).
3 发射波形及电阻率对异常响应的影响
假设均匀半空间中存在一个100 m×100 m×400 m的地质体,围岩电阻率为100 Ωm,网格剖分为10 m×10 m×40 m.发射和接收线圈中心的高度分别为30 m和50 m,发射与接收线圈水平距离为10 m.异常体中心位置在地面上的投影作为坐标原点,取Z轴向下为正,如图1所示.发射波形考虑两种情况:第一种为半正弦波,基频30 Hz,脉冲宽度为4 ms;第二种为梯形波,基频30 Hz,上升沿和下降沿时间均为0.2 ms,稳定电流时间为3.6 ms.发射偶极距为615000 Am2.
首先对基频为30 Hz的半正弦波和梯形波的垂直磁场及磁感应的时间域响应进行了计算,得到其随地质体埋藏深度变化的曲线,如图2所示.
从图2可以看出,磁场B和磁感应dB/dt保持良好的微分/积分关系,且无论半正弦波或梯形波,B和dB/dt在on-和off-time都存在响应极大值.地下存在异常体时的时间域响应与均匀半空间的响应
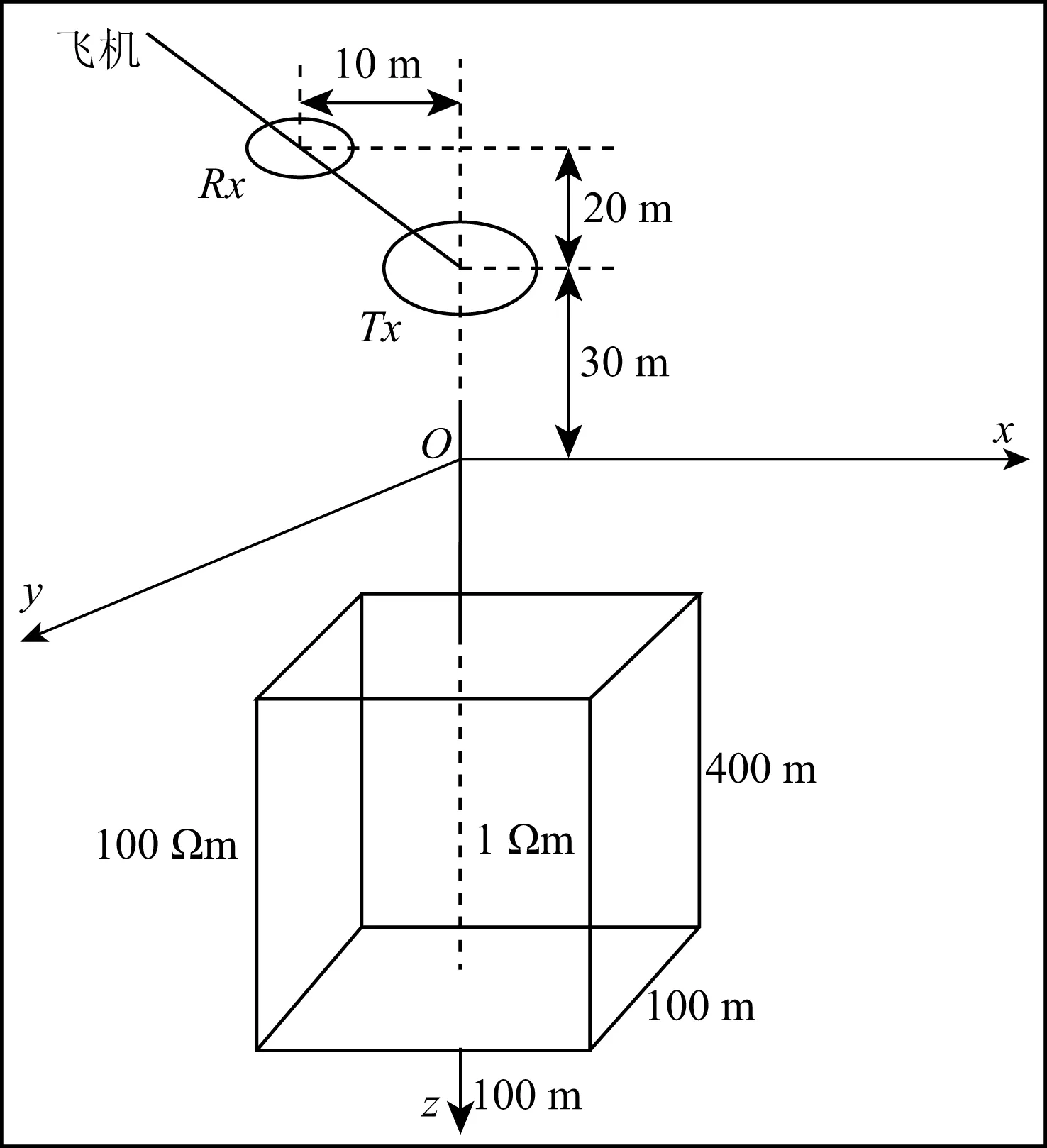
图1 模型示意图Fig.1 Sketch map of AEM system and the 3D earth model
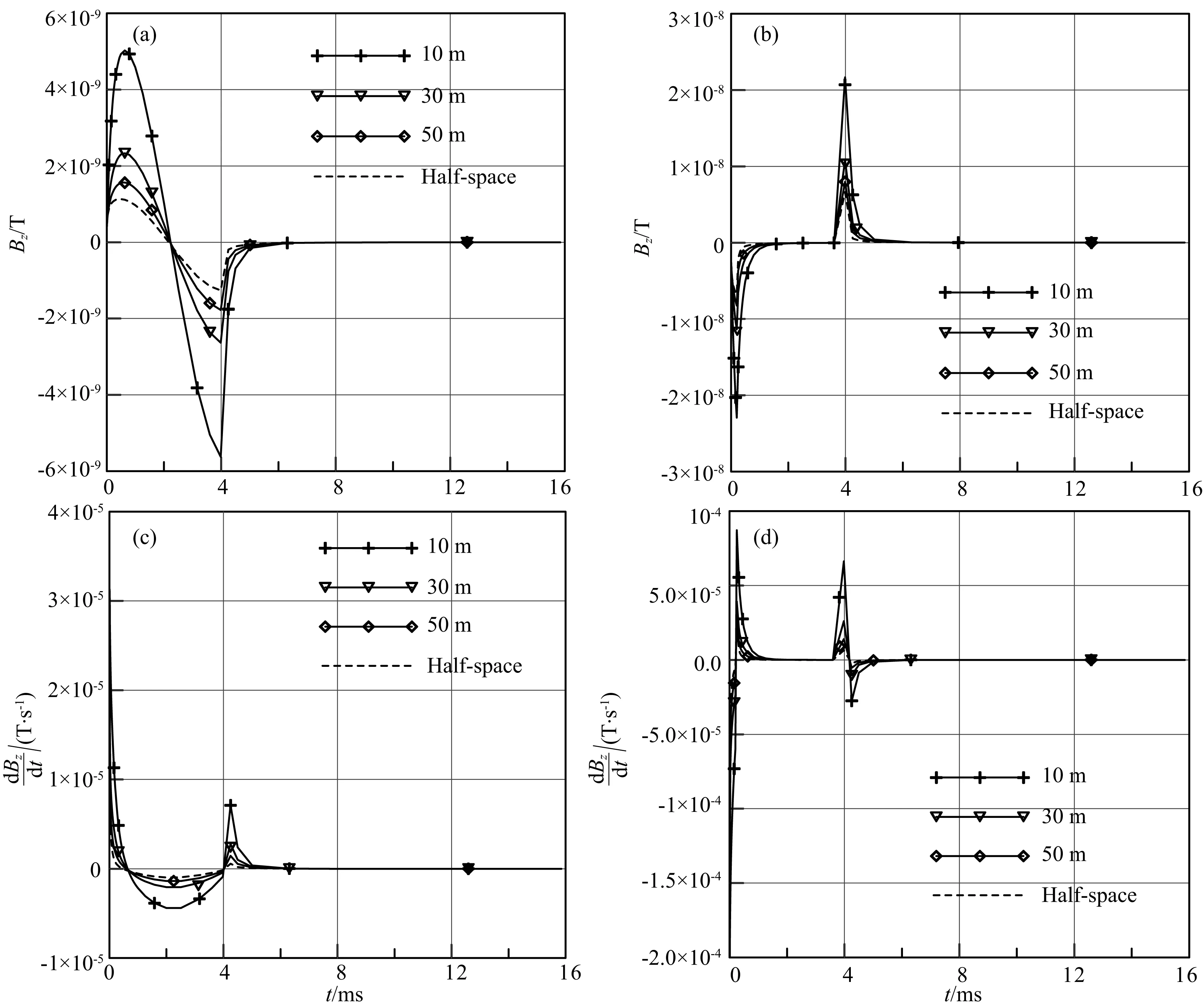
图2 B和dB/dt时间域响应随深度变化(a,c)分别为发射半正弦波时的B和dB/dt响应曲线;(b,d)分别为发射梯形波时的B和dB/dt响应曲线.Fig.2 Time-domain AEM responses B and dB/dt versus depth(a) and (c) are half-sine B and dB/dt responses, respectively; (b) and (d) are trapezoid B and dB/dt responses, respectively.
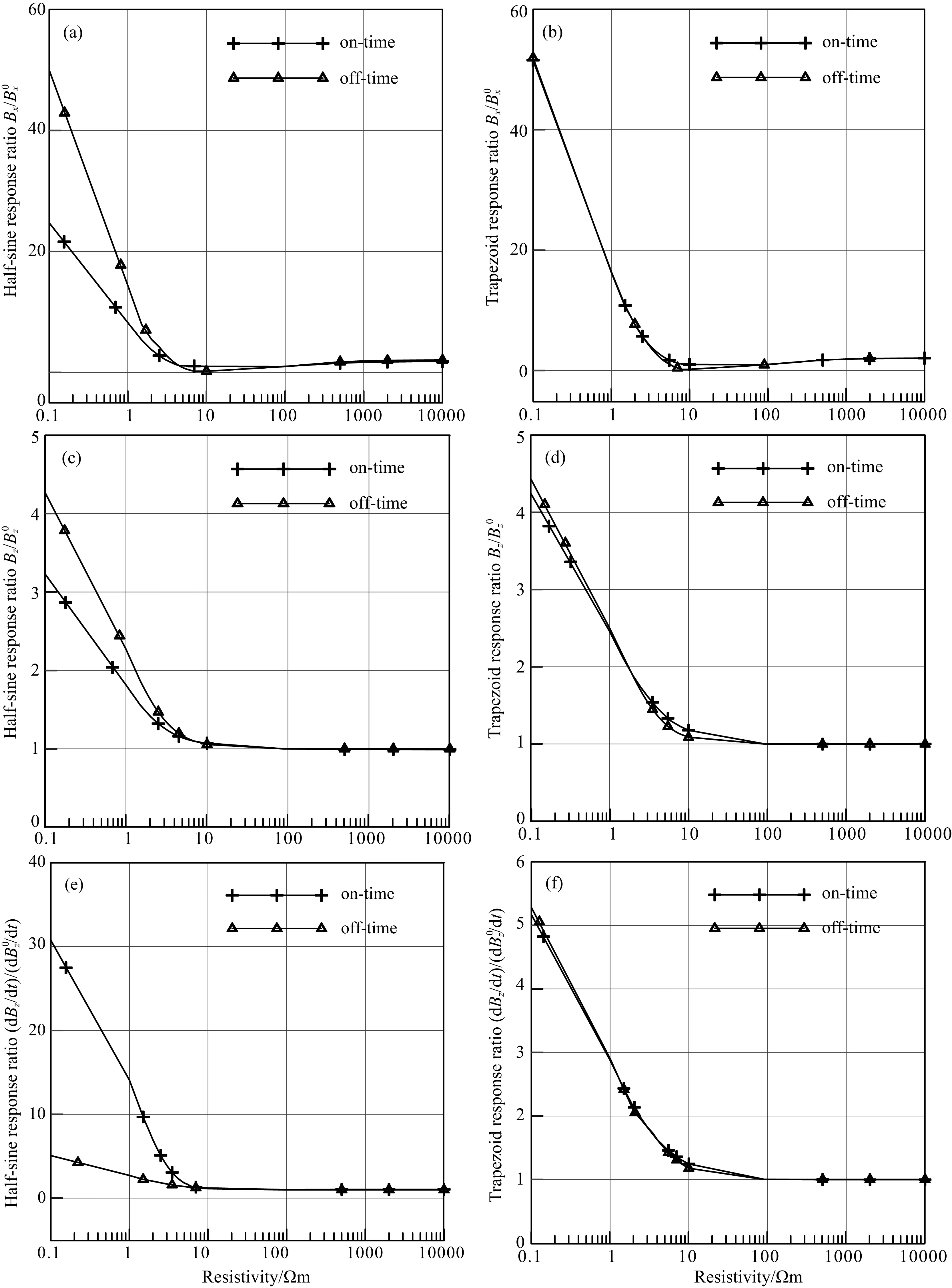
图3 响应比随异常体电阻率变化曲线(a)、(c)和(e)分别代表发射半正弦波时Bx、Bz和dBz/dt与半空间响应的比值随电阻率变化曲线;(b)、(d)和(f)分别代表发射梯形波时Bx、Bz和dBz/dt与半空间响应的比值随电阻率变化曲线.Fig.3 Time-domain EM response ratios versus resistivity(a), (c) and (e) are ratios of Bx, Bz and dBz/dt for a half-sine wave to half-space responses versus resistivity; (b), (d) and (f) are ratios of Bx, Bz and dBz/dt for a trapezoid wave to half-space responses versus resistivity
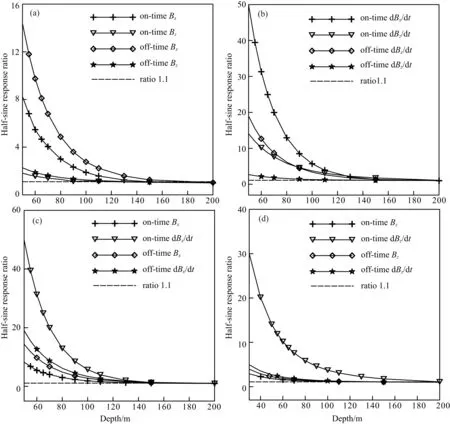
图5 半正弦波B和dB/dt的勘探深度对比(a) on- 和off-time期间的Bx和Bz响应比随深度变化;(b) on- 和off-time期间的dBx/dt和dBz/dt响应比随深度变化;(c) on-和off-time期间的Bx和dBx/dt响应比随深度变化;(d) on-和off-time期间的Bz和dBz/dt响应比随深度变化.Fig.5 Exploration depth of B and dB/dt for a half-sine wave(a) on- and off-time Bx and Bz response ratios varying with depth; (b) on- and off-time dBx/dt and dBz/dt response ratios varying with depth; (c) on- and off-time Bx and dBx/dt response ratios varying with depth; (d) on- and off-time Bz and dBz/dt response ratio varying with depth.
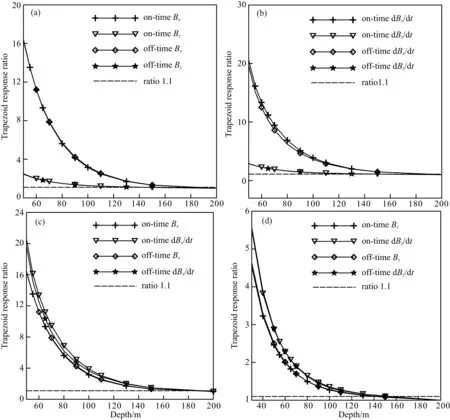
图6 梯形波B和dB/dt的勘探深度对比(a) on- 和off-time期间的Bx和Bz响应比随深度变化;(b) on- 和off-time期间的dBx/dt和dBz/dt响应比随深度变化;(c) on- 和off-time期间的Bx和dBx/dt响应比随深度变化;(d) on- 和off-time期间的Bz和dBz/dt响应比随深度变化.Fig.6 Exploration depth of B and dB/dt for a trapezoid wave(a) on- and off-time Bx and Bz response ratios varying with depth; (b) on- and off-time dBx/dt and dBz/dt response ratios varying with depth; (c) on- and off-time Bx and dBx/dt response ratios varying with depth; (d) on- and off-time Bz and dBz/dt response ratio varying with depth.

图7 不同波形B和dB/dt的勘探深度对比(a)—(d)发射波形为半正弦波; (e)—(h)发射波形为梯形波. (a)和(e)为Bz响应的on- 和off-time勘探深度对比图;(b)和(f)为dBz/dt响应的on-和off-time勘探深度对比图;(c)和(g)为on-time的Bx和dBx/dt勘探深度对比图;(d)和(h)为on-time的Bz和dBz/dt勘探深度对比图.Fig.7 Exploration depth of B and dB/dt for different transmitting waveforms(a)—(d) Half-sine transmitting waves; (e)—(h) Trapezoid transmitting waves. (a) and (e) are on- and off-time Bz exploration depth; (b) and (f) are on- and off-time dBz/dt exploration depth; (c) and (g) are on-time Bx and dBx/dt exploration depth; (d) and (h) are on-time Bz and dBz/dt exploration depth.
曲线趋势十分一致,并随着深度的不断增加,响应值不断接近半空间响应.由于探测分辨率限制,航空电磁系统无法识别所有高于半空间背景响应的异常.本文以异常响应值到达均匀半空间背景响应的10%的信号作为最小可识别信号,其对应的探测深度定义为最大探测深度.
地质体的电阻率变化会引起异常响应变化,使探测能力发生变化.当异常体电阻率从0.1 Ωm变化到10000 Ωm时,总响应与均匀半空间背景响应之比的变化规律如图3所示.
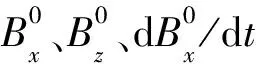
4 低阻区探测能力分析
4.1 记录点位置
非对称航空电磁系统的记录点由模型试验确定.取异常体电阻率为1 Ωm,异常体埋深为100 m,发射基频为30 Hz.图4为沿飞行剖面的各磁场和磁感应分量的时间域响应.图中横坐标为发射线圈中心对应地面测线上的位置,纵坐标为存在目标体的时间域响应与均匀半空间响应的比值.
根据剖面结果,以时间域二次场响应最大值处作为记录点位置,可以确定各场分量Bx、Bz及磁感应分量dBx/dt和dBz/dt在探测异常体最大埋深时的发射线圈的位置.经计算,对于半正弦波,可得Bx、Bz、dBx/dt、dBz/dt记录点位置对应x、y坐标分别为(40.94 m,0),(-4.45 m,0),(33.49 m,0),(-4.45 m,0);对于梯形波,其Bz和dBz/dt响应值最大时记录点位置对应坐标均为(-4.45 m,0).
4.2 探测能力分析
在确定异常记录点位置的基础上,本文对不同发射波形、不同时间道情况下的Bx、Bz和dBx/dt、dBz/dt进行了勘探深度的比较和分析.图5为发射半正弦波时,磁场分量和磁感应各分量响应比随异常体埋深的变化;图6为发射梯形波时,响应比随异常体埋深的变化.其中横轴表示深度,纵轴为航空电磁响应与均匀半空间响应之比.
由图5可见,随着地质体埋藏深度的不断增加,on-和off-time的最大响应不断减小.图5a显示,同线磁场分量Bx在on-和off-time期间的探测深度均大于垂向磁场分量Bz;同时,off-time的磁场分量的探测深度大于on-time;图5b显示off-time的垂向磁感应分量,从异常体埋深较浅至最大深度变化过程中,其二次场响应都相对较小;图5(c,d)显示,无论on-time或off-time,磁感应同线分量dBx/dt的探测深度大于磁场Bx的探测深度;垂向分量dBz/dt的探测深度大于Bz的探测深度.
如图6所示,当发射波形为梯形波时,对于同一磁场或磁感应分量,其on-time和off-time期间的探测深度十分接近,但不同分量间存在一定差别.通过对比图6(a—d)发现,Bx的探测深度大于Bz,且垂向磁感应分量dBz/dt探测能力弱于dBx/dt;同时,dBx/dt的探测能力强于Bx,dBz/dt的探测能力强于Bz,这与发射半正弦波时结论相似.
通过计算,得到半正弦波和梯形波各磁场分量和磁感应分量的on-和off-time所对应的勘探深度情况如表1所示.
表1数据显示,对于柱状良导体,在on-time和off-time过程中,不同发射波形、不同磁场和磁感应分量,对应不同的勘探深度.发射半正弦波时的探测能力分析结论与发射梯形波时结论相似.航空测量可根据实际地质条件选择合适的参量组合进行最优观测和数据解释.

表1 磁场B和磁感应dB/dt的探测深度Table 1 Exploration depth for magnetic field B and magnetic induction dB/dt
5 中阻区探测能力分析
取异常体电阻率为10 Ωm,其他参数选择与前述柱状良导体一致.利用类似于低阻区勘探能力分析方法,可以获得该地质条件下不同磁场及磁感应分量间的探测能力.
如图7所示,当发射半正弦波时,垂向磁场分量Bz及磁感应分量dBz/dt在on-time的勘探深度大于off-time的勘探深度,且磁感应分量的探测深度在on-time还是off-time都大于对应的磁场分量;当发射波形为梯形波时,垂向磁场和磁感应分量各自的探测能力在on-和off-time期间相当,且on-和off-time时的同线磁感应分量的探测深度比磁场分量的探测深度稍大.经过计算,不同波形时的各分量的探测深度对比见表2.

表2 磁场B和磁感应dB/dt的探测深度(模型电阻率10 Ωm)Table 2 Exploration depth for B and dB/dt for a model of 10 Ωm
表2显示的是相同地质体条件下(中阻区),不同发射波形时,相应磁场和磁感应分量的探测深度值.可以看出,大部分同一分量的on-和off-time的相对探测能力结论与低阻区的结论相反,其他各交差分量间的探测能力分析结论与低阻区一致.
6 不同尺寸异常体的探测能力分析
当地质体形状、尺寸和电阻率发生变化时,航空电磁响应及探测能力随之变化.这里仅介绍垂直薄板和水平良导板的探测情况,所使用参数与低阻区探测能力分析时采用的模型一致.模型尺寸与勘探深度对比如表3所示.
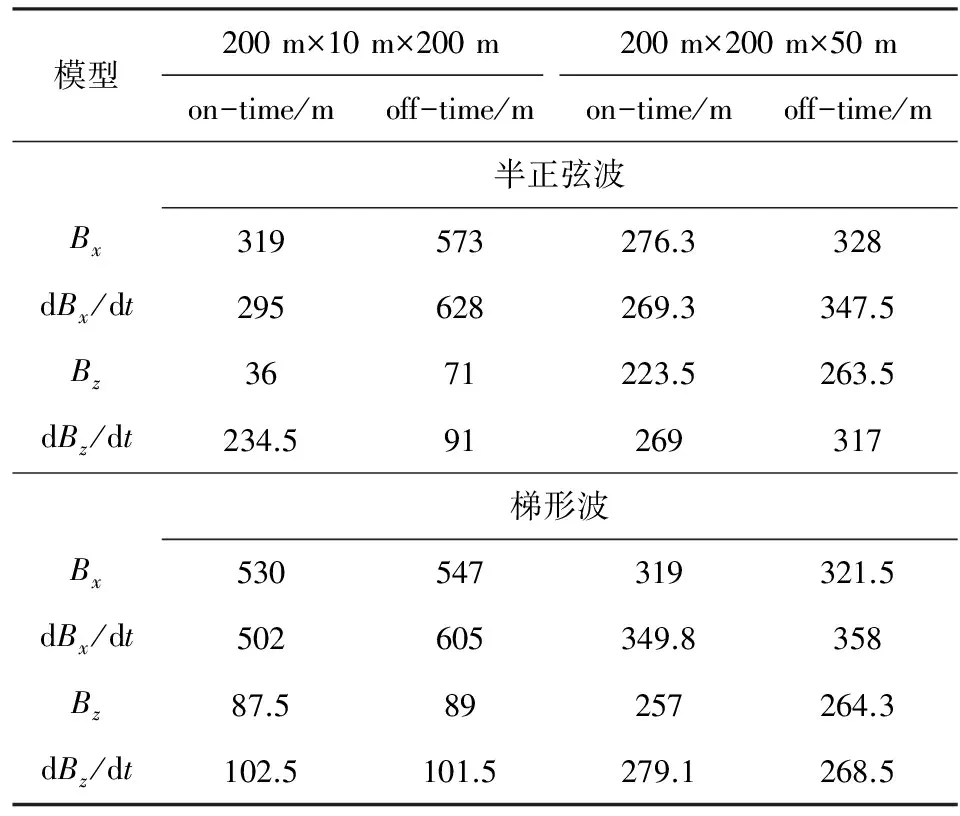
表3 磁场B和磁感应dB/dt的探测深度Table 3 Exploration depth for B and dB/dt
由表3可知,对于直立良导薄板,无论发射半正弦波还是梯形波,垂向磁场分量探测能力明显弱于同线分量的探测能力,这与电磁基本理论相吻合.在off-time期间,磁感应分量的探测深度均大于其对应的磁场分量的探测深度.对于水平良导板状体,发射梯形波时,on- 和off-time的探测深度依然接近.实际航空电磁观测中,需要针对特定地质情况进行模型设计和正演计算分析,以获得特定探测目标的航空电磁参量组合,指导野外探测和数据解释.
7 结论
本文在时间域航空电磁法勘探原理和算法的基础上,以均匀半空间中三维良导体为例,进行了半正弦波和梯形波激励下的各磁场及磁感应分量的on-和off-time时间域响应的计算.通过对比分析,得出对深部异常体勘探能力的结论如下:
1) 对于非对称航空电磁系统而言,记录点的位置可以通过数值试验来确定;
2) 对于柱状良导体,无论on-还是off-time,同线磁场分量Bx的探测深度均大于垂向磁场分量Bz,磁感应分量的探测深度均大于其对应的磁场分量的探测深度;
3) 发射波形不同,航空电磁对地质体的探测能力不同,梯形波的同一个场分量在on-time和off-time期间的探测深度差别较小;
4) 地质体的形状和尺寸对磁场和磁感应分量在on-和off-time的相对探测能力产生影响.实际航空电磁的观测设计中,我们应根据勘探目标的特征,选择具有最佳偶合的观测系统,分析其对目标体的探测能力,针对设定的模型进行计算和分析,以获得最佳参数.
根据以上结论及本文研究思想,可以针对具体的勘探目标,设计一套最佳航空电磁观测系统参数组合,以保证在有效完成勘探目标探测的前提下,减少航空观测的工作量、提高工作效率.
致谢 贲放和黄威博士在文章准备过程中提供的帮助及审稿人对本文提出的修改意见一并衷心感谢.
Balch S J, Boyko W P, Paterson N R. 2003. The AeroTEM airborne electromagnetic system.TheleadingEdge, 22(6): 562-566.
Chen S D, Lin J, Zhang S. 2012. Effect of transmitter current waveform on TEM response.ChineseJ.Geophys. (in Chinese), 55(2): 709-716, doi: 10.6038/ j.issn.0001-5733. 2012.02.035.Huang H P, Wang W Z. 1990. Inversion of time-domain airborne electromagnetic data.ChineseJ.Geophys. (in Chinese), 33(1): 88-97.Huang H P. 1991. The theoretical problems of the application of airborne electromagnetic method in engineering geophysical exploration (in Chinese). ∥ The Academic Essays of the 7th Chinese Geophysical Society.
Liu G. 1998. Effect of transmitter current waveform on airborne TEM response.ExplorationGeophysics, 29(2): 35-41.
Luo Y Z, Zhang S Y, Wang W P. 2003. A research on one-dimension forward for aerial electromagnetic method in time domain.ChineseJ.Geophys. (in Chinese), 46(5): 719-724, doi: 10.3321/j.issn:0001-5733.2003.05.021.
Pei Y F, Yin C C, Liu Y H, et al. 2014. Calculation and application of B-field for time-domain airborne EM.ProgressinGeophysics(in Chinese), 29(5): 2191-2196, doi: 10.6038/pg20140530.
Raiche A P. 1974. An integral equation approach to Three-Dimensional modelling.GeophysicalJournaloftheRoyalAstronomicalSociety, 36(2): 363-376.Raiche A. 2001. 3D EM modeling using integral equation algorithm. AMIRA Project Report P223E.
Smith R, Annan P. 1998. The use of B-field measurements in an airborne time-domain system: Part Ⅰ: Benefits of B-field versus dB/dt data.ExplorationGeophysics, 29(2): 24-29.
Xu Y C, Lin J, Li S Y, et al. 2012. Calculation of full-waveform airborne electromagnetic response with three-dimension finite-difference solution in time-domain.ChineseJ.Geophys. (in Chinese), 55(6): 2105-2114, doi: 10.6038/j.issn.00015733.2012.06.032.Yin C, Huang W, Ben F. 2013. The full-time electromagnetic modeling for time-domain airborne electromagnetic systems.ChineseJ.Geophys. (in Chinese), 56(9): 3153-3162, doi: 10.6038/cjg20130928.
Yin C, Smith R S, Hodges G, et al. 2008. Modeling results of on-and off-time B and dB/dt for time-domain airborne EM systems. ∥ 70th Annual EAGE Conference and Exhibition, Extended Abstract, Rome, 1-4.
附中文参考文献
陈曙东, 林君, 张爽. 2012. 发射电流波形对瞬变电磁响应的影响. 地球物理学报, 55(2): 709-716, doi: 10.6038/j.issn.0001-5733.2012.02.035.
黄皓平, 王维中. 1990. 时间域航空电磁数据的反演. 地球物理学报, 33(1): 88-97.
黄皓平. 1991. 航空电磁法在工程物探中应用的理论问题. ∥ 中国地球物理学会第七届学术年会论文集.
罗延钟, 张胜业, 王卫平. 2003. 时间域航空电磁法一维正演研究. 地球物理学报, 46(5): 719-724, doi: 10.3321/j.issn:0001-5733.2003.05.021. 裴易峰, 殷长春, 刘云鹤等. 2014. 时间域航空电磁磁场计算与应用. 地球物理学进展, 29(5): 2191-2196, doi: 10.6038/pg20140530. 许洋铖, 林君, 李肃义等. 2012. 全波形时间域航空电磁响应三维有限差分数值计算. 地球物理学报, 55(6): 2105-2114, doi: 10.6038/j.issn.00015733.2012.06.032.
殷长春, 黄威, 贲放. 2013. 时间域航空电磁系统瞬变全时响应正演模拟. 地球物理学报, 56(9): 3153-3162, doi: 10.6038/cjg20130928.
(本文编辑 汪海英)
Exploration capability of airborne TEM systems for typical targets in the subsurface
YIN Chang-Chun1, REN Xiu-Yan1*, LIU Yun-He1,2, CAI Jing1
1CollegeofGeo-explorationScienceandTechnology,JilinUniversity,Changchun130026,China2HubeiSubsurfaceMulti-scaleImagingLab(SMIL),ChinaUniversityofGeosciences(Wuhan),Wuhan430074,China
For airborne EM (AEM) systems, flight altitude, transmitting waveforms, transmitting dipole moment and base frequency can strongly affect the depth of exploration. In an AEM survey, if all the magnetic field and magnetic induction components are measured, the EM dataset will be huge,resulting in costly data processing. In this paper, we investigate the exploration capability of an AEM system to different targets in the subsurface. We try to optimize parameter combinations of the airborne system (e.g. the waveform, field components, on- and off-time etc.) to balance the survey cost and resolution of targets.For the towed-bird AEM system, we use an integral equation algorithm to calculate the frequency-domain EM field responses and convert them into the time domain via a Hankel′s transform. The on- and off-time magnetic fieldsBand magnetic induction dB/dtare calculated for 3D targets of a plate or a prism embedded in a conductive earth. We propose a response ratio to define the largest exploration depth, based on which we calculate the exploration depth to different underground targets for different transmitting waves, field components and on- and off-time signals.We study and analyze the influence of transmitting waveforms, field components, the on- and off-time signals on the target exploration capability. We find that the off-timeBx, dBx/dt, and dBz/dtfor a trapezoid transmitting wave is the best parameter combination for resolving an underground conductive prism target. For a vertical thin plate, however, the off-timeBx, dBx/dtand on-time dBz/dtfor a half-sine transmitting wave perform better. The combination of off-timeBx, dBx/dtand on-timeBz, dBz/dtfor a trapezoid waveform can make deeper exploration for a horizontal thick plate.From the research in this paper, we draw the conclusion that depending on the exploration target, there exists an optimal parameter combination of the AEM system that can achieve the maximum exploration capability. This will guide AEM survey design and data processing for an effective and efficient exploration. This research further lays the foundation for establishment of AEM standards and regulations.
Airborne EM; Time-domain; Exploration capability; System design; Magnetic field and magnetic induction; On- and off-time
殷长春,任秀艳, 刘云鹤.2015.航空瞬变电磁法对地下典型目标体的探测能力研究.地球物理学报,58(9):3370-3379,
10.6038/cjg20150929.
Yin C C, Ren X Y, Liu Y H,et al. 2015. Exploration capability of airborne TEM systems for typical targets in the subsurface.ChineseJ.Geophys. (in Chinese),58(9):3370-3379,doi:10.6038/cjg20150929.
10.6038/cjg20150929
P631
2015-02-05,2015-06-27收修定稿
国家自然科学基金项目(41274121),国家重大科研装备研究项目(ZDYZ2012-1-03和20130523MTEM05),中国地质大学(武汉)地球内部多尺度成像湖北省重点实验室开放基金项目(SMIL-2014-03)联合资助.
殷长春,男,1965年生,教授,主要从事电磁勘探理论,特别是航空和海洋电磁方面的研究.E-mail:yinchangchun@jlu.edu.cn
*通讯作者 任秀艳,女,1989年生,硕士,主要从事航空电磁探测能力、时间域有限差分方法研究.E-mail:jdrxy@hotmail.com
