基于射线追踪技术计算地震定位中震源轨迹的改进方法

赵爱华, 丁志峰, 白志明

1 中国地震局地球物理研究所, 北京 100081 2 中国科学院地质与地球物理研究所， 北京 100029



基于射线追踪技术计算地震定位中震源轨迹的改进方法

赵爱华1, 丁志峰1, 白志明2

1 中国地震局地球物理研究所, 北京 100081 2 中国科学院地质与地球物理研究所， 北京 100029

使用震源轨迹确定震源位置不仅稳健而且直观，但当介质复杂时震源轨迹难以给出解析解.基于最小走时树射线追踪技术计算震源轨迹的方法(以轨迹所在的残差场中残差最小的点(初始点)至残差较小的点(震源轨迹代表点)的射线路径表示震源轨迹)适用于复杂速度模型，但尚不能正确计算由多段组成的震源轨迹，同时兼顾计算轨迹的完整性和精细性较为困难，计算参数设置烦琐不适于大批量数据的自动处理.针对该方法存在的问题，本文对其进行了改进：(1)采用一种“削皮”算法选取震源轨迹所经过的模型单元的节点作为轨迹代表点；(2)将残差较小的区域作为震源轨迹计算区域(该区域依轨迹分布自适应地划分为若干个连通区域)，从未计算的轨迹代表点中选取残差最小者作为射线路径初始点，利用最小走时树算法依次计算所有连通区域内的震源轨迹；(3)通过去掉较短的不再分叉的射线路径使震源轨迹更为精细.虚拟和真实事件的算例表明，改进方法有效克服了原方法的不足，可便捷地计算复杂速度模型中事件的震源轨迹，计算的轨迹精细且较完整.

地震定位； 震源轨迹； 射线追踪； 最小走时树方法； “削皮”算法

1 引言

地震定位在地震活动性分析、核爆监测及地球深部结构的研究等中起着十分重要的作用(曾融生, 1991；丁志峰等，1999；Richards et al., 2006；陈运泰，2009).为更好地确定震源位置与发震时间参数，地震学家发展了多种定位方法(田玥和陈晓非，2002；蔡明军等，2004；杨文东等，2005)，例如盖革法(Geiger, 1912)、双差法(Waldhauser and Ellsworth, 2000)、网格搜索法(Shearer, 1997)、交切法(Pujol, 2004; 廉超等, 2006；周建超和赵爱华，2012)以及逆时成像法(许力生等，2013a, 2013b)等.这些方法各有特点，其中交切法不仅原理简单，而且稳健直观，在地震台网中有广泛的应用(孟玉梅等, 2001; 宋锐等, 2001).交切法使用震源轨迹确定震源位置，即使仅有少量的观测数据，也能得到有价值的震源位置信息(赵爱华等, 2008).交切法的缺点是定位精度较低，特别是震源深度(Udías, 1999).交切法定位精度低的主要原因是它基于均匀或横向均匀介质模型(此时震源轨迹可准确求解)，而实际上地球内部存在着较强的横向非均匀性.使用远离实际的速度模型必然导致或大或小的定位误差(Billings et al., 1994; Chen et al., 2006).因此，提高交切法定位精度的关键是使之基于更接近实际的速度模型.此外，得益于地震台网建设和反演技术发展，愈加广泛的区域建立了较精细的三维结构模型，全球尺度图像的分辨率也不断提高，使基于三维速度模型进行高精度定位成为可能.

将传统交切法扩展至三维速度模型需要解决的首要问题是震源轨迹计算.当速度结构复杂时，震源轨迹难以表达成解析形式.对于复杂介质中震源轨迹的计算问题，目前主要有两种解决方案.一是以近似满足震源轨迹方程的点表示震源轨迹，近似的程度以方程容差表征(Zhou，1994；Font et al., 2004；Theunissen et al., 2012).这种方法简单易行，自适应性强，对震源轨迹的几何形态没有限制，其缺点是得到的震源轨迹较为粗略，特别是当方程容差取得较大时：即使到时和速度模型都准确，震源轨迹也不会交于一点，而是交会成一个区域.另外一种方案基于最小走时树射线追踪技术：震源轨迹以其所在残差场中残差最小的点(初始点)至残差较小的点(作为轨迹代表点)的射线路径进行表示(赵爱华等，2008).这种方法可精细计算震源轨迹，根据震源轨迹的方位分布可直观地评估定位效果，分析速度模型、到时拾取精度及台站分布等因素对定位结果的影响.其缺点是：1)不能处理由多段组成的震源轨迹.由于仅选取残差场中最小的点为射线路径初始点，所有轨迹代表点均与该点相连，当震源轨迹由分开的多段组成时会产生虚假轨迹(即穿过两段轨迹之间区域的射线路径)；2)选取轨迹代表点烦琐费时，不适于大批量数据的自动处理.震源轨迹代表点按全部模型节点的百分比选取，轨迹代表点的百分比应依轨迹长度而设，而轨迹长度很难预知；3)难以同时兼顾计算轨迹的完整性与精细性.即使准确知道轨迹长度，由于轨迹所经过模型单元的节点处的残差并不相同，单纯根据残差大小选取的轨迹代表点要么不能完整表征轨迹要么冗余使轨迹较为粗略.现代地震台网记录的地震事件及观测数据数量都是巨大的，大量事件的高精度定位，要求震源轨迹的计算不仅准确而且效率要高.

由以上可知，复杂介质中震源轨迹的计算方法还需完善.本文尝试对基于射线追踪技术的计算方法(赵爱华等，2008)进行改进以克服其不足.为叙述方便，方法说明以二维模型为例.

2 震源轨迹方程

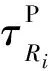
2.1 到时差约束的震源轨迹

(1)

即考虑到计算误差，震源轨迹在到时差残差场

FRDT(x;Rj1,Wj1;Rj2,Wj2)=|T(x;Rj1,Wj1)

(2)

中具有接近于0的低值，其中I(x)=1.

2.2 到时约束的震源轨迹

根据观测到时可构建事件的发震时间场(赵爱华, 2014)

(3)

其中，Gj和Wj分别为第j个观测到时的台站和震相类型(P或S波)，K为观测到时个数.这样，第j个到时约束的震源轨迹满足如下方程：

(4)

即考虑到计算误差，震源轨迹在到时残差场

FRAT(x,Gj,Wj)=

(5)

中具有接近于0的低值，其中I(x)=1.

方程(1)和(4)，仅当介质速度结构较为简单时才存在解析解.与到时差约束的震源轨迹不同，到时约束的震源轨迹即使对于均匀介质也比较复杂，特别是当发震时间场使用较多到时构建时.考虑P波和S波速度分别为6.0km·s-1和3.6km·s-1、尺度为150km×90km的均匀介质模型.将模型剖分成3km×3km的正方形单元.设在点x0(37.5km,-31 .5km)处，时间t0=0 s时发生地震，记录到该事件P和S波初至的台站有5个，分别为Ri(13.5+(i-1)× 30.0 km,-1.5 km)(i=1,2,3,…,5).该事件的发震时间场及台站R3处P波的到时残差场灰度图像如图1所示.可以看到：1)P波到时单独构建的发震时间场(图1a)与P和S波到时联合构建的发震时间场(图1b)具有相似的结构，这是因为P波与S波的速度之比为常数；2)单独P波到时约束的震源轨迹(图1c)、P和S波到时联合约束的震源轨迹(图1d)均较为复杂，既非圆亦非双曲线，特别是后者由分开的两段组成；3)对于同一到时，发震时间场不同，其震源轨迹也不同，甚至相差较大.需要指出的是，为突出显示震源轨迹，到时残差进行了取对数处理.

3 轨迹计算

由图1(c,d)可以看出，残差较小(例如小于0.2 s)的区域依震源轨迹的分布划分为1个(图1c)或多个(图1d)连通区域.由于震源轨迹在残差场中表现为低值，因此若在每个连通区域内残差最小点处激发地震波，地震波将沿该连通区域内的震源轨迹快速传播，而在轨迹两侧特别是连通区域外传播较慢，此时将残差看作地震波慢度.这样，若选取部分单元节点作为震源轨迹的代表点，则代表点至与其同一连通区域内地震波初始点的射线路径可近似地表示震源轨迹，且不存在虚假震源轨迹问题.为处理方便，通常以残差小于阈值的点作为震源轨迹的代表点(Zhou,1994;赵爱华等，2008)，由于震源轨迹所经过节点其残差并不相同(在图1(c，d)中表现为灰度不同)，因而难以同时兼顾计算轨迹的完整性和精确性.与之相比，若以震源轨迹所经过节点为其代表点，则计算震源轨迹即较完整也较精细.基于以上认识，我们提出改进的震源轨迹计算方法.

图1 均匀介质中事件的发震时间场(a和b)和到时残差场灰度图像(c和d)(a) P波到时构建; (b) P与S波到时构建; (c)和(d) 分别对应(a)和(b)，同一P波到时约束. 发震时间的等值线间隔为2.0 s，红色“+”为震源；到时残差场中，绿线为0.2 s的到时残差等值线，蓝色实线和红色虚线分别为震源轨迹的计算结果与理论解，黄色点为选定的震源轨迹代表点.Fig.1 Origin time fields (a, b) and arrival time residual fields (c, d) of an event in a homogeneous medium(a) P-wave arrival times; (b) P- and S-wave data; (c) and (d) one P-wave arrival time jointed with the origin time fields (a) and (b), respectively. The origin time contour interval equals 2.0 s, and the red crosses indicate the hypocenter. In the residual fields, the green lines are contours of 0.2 s. The blue solid and red dashed lines respectively show the calculated and theoretical focal loci. The yellow dots indicate the selected hypocentral locus reference points.

3.1 震源轨迹代表点的选取

在图1(c，d)中，震源轨迹位于残差较小连通区域内的中间，犹如位于果中之核.震源轨迹所经过的单元节点，其残差尽管有大有小，但与轨迹两侧节点相比为最小.据此特点可采用类似层层削去果皮得到果核的方法求取这些节点.为便于叙述，将残差小于RFLRP的单元节点称为震源轨迹代表点的初选点，其集合记为Θ.从初选点集合Θ中选取震源轨迹代表点的步骤如下：

(1)分类

对于节点i∈Θ，若其邻点均在集合Θ内，则i为Θ的内部点，内部点集合记为I；否则i为Θ的外表点，外表点集合记为O.

(2)更新

对于节点i∈O，若其邻点中没有内部点或有内部点但残差都较i点大，则保留该点；否则将i点从集合O中移出.之后，将集合Θ更新为O与I之并集.

(3)迭代条件检测

若内部点集合I为空集，则转到步骤(4)；否则回到步骤(1).

(4)精简

集合O中有时包括两列沿震源轨迹并排分布的外表点.由于单列点足以表征震源轨迹，因此还需对集合O进行精简.对于节点i∈O及与之相邻的外表点，当这些点的个数超过3个时，则仅保留其中残差最小的3个.

(5)纯化

当残差场的结构较为复杂时，集合O中可能会有少数异常点，并非震源轨迹所经过节点.这些异常点残差相对较大.这里，将残差超过集合O中点平均值2倍均方差的点视为异常点，并将其从集合O中移出.

在上述算法中，步骤(1)—(3)是用类似层层削皮的方式去掉初选点集合中的外表点；步骤(4)是去掉多余的代表点；步骤(5)是去掉假的代表点.最后保留的集合O中的点作为震源轨迹代表点.图1(c，d)中黄色点是从残差小于0.2s的初选点中选取的震源轨迹代表点.可以看出，选取的代表点仅为震源轨迹所经过节点其中的一部分，但很好地表征了震源轨迹的形态，这对计算震源轨迹来说已足够.实际上，以射线路径表示震源轨迹，若能仅选取每段震源轨迹上残差最小的点及两端节点作为代表点更为理想，但实现较为困难.

3.2 射线路径计算

表示震源轨迹的射线路径利用改进的最小走时树方法(Zhao et al., 2004)计算.最小走时树射线追踪方法(Nakanishi and Yamaguchi, 1986; Moser, 1991)基于地震学中的惠更斯原理和费玛原理，具有稳健性好、适用复杂模型的优点.该方法通过构建最小走时树的方式计算地震波从震源至所有模型单元节点的走时和射线路径(Cao and Greenhalgh., 1993).对于由分开的多段组成的震源轨迹，为防止产生虚假轨迹，需从包含每段轨迹的连通区域内选出残差最小的点作为地震波初始点.震源轨迹的形态分布难以预知，同时选出其每段轨迹的地震波初始点是困难的.由最小走时树算法的终止条件可知其运行区域为连通区域.这样，若将射线路径的计算区域限制为残差较小的区域，则可通过依次为其每个连通区域指定地震波初始点的方式，利用最小走时树算法逐段计算出全部震源轨迹.注意到震源轨迹代表点包含了每个连通区域残差最小的点，因此地震波初始点可从轨迹代表点中选取.

将射线路径计算的区域限定为残差小于RFL的区域Ω(这可通过将Ω外的节点设置为已得到最小走时的点来实现).从残差小于RFLRP的单元节点中选取的震源轨迹代表点集合，这里记为Z.参数RFL和RFLRP可相同也可不同.表示震源轨迹的射线路径计算步骤如下：

(1)查找地震波初始点

在震源轨迹代表点集合Z中查询残差最小的点s,将s从Z中移出；

(2)射线路径计算

以s为地震波初始点，在残差场中计算地震波走时及射线路径直至最小走时树算法终止；若节点j∈Z被计算过，则将其从Z中移出.

(3)迭代条件检测

如果Z成为空集则结束；否则回到步骤(1).

3.3 震源轨迹修饰

震源轨迹代表点大多仅近似满足轨迹方程.当其数量过多时，计算的震源轨迹将不很精细，需要做进一步的修饰处理.

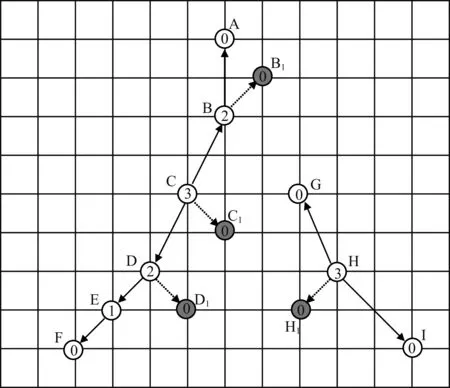
图2 以射线路径表示的震源轨迹示意图Fig.2 A diagram of one hypocentral locus represented with ray paths

震源轨迹代表点至其各自地震波初始点的射线路径形成树状结构，如图2所示.若将射线路径(即图2中有向线段)看作枝条，则射线经过的节点则为枝条生发点，当其生发的枝条数(圆圈内数字)大于或等于2时该点为分杈点.轨迹代表点沿震源轨迹分布，因此射线路径树的主干(即射线路径经过次数nFLP较多的代表点至地震波初始点射线路径，例如线段BCD)应在实际震源轨迹上.如果仅取该部分(赵爱华 等，2008)，将可能会损害轨迹的完整性.例如，取nFLP=2，则将遗失图2中的震源轨迹段GHI.为此，在对震源轨迹修饰时，我们是去掉长度Ltwig较小的不再分杈的枝条，例如图2中虚线所示部分.

图1(c，d)中的震源轨迹，Ltwig=2(以模型单元的边长为单位)时的计算结果如图中蓝线所示.可以看出，计算的震源轨迹和理论结果(图中红色虚线)符合得很好.值得指出的是，若将模型剖分为更小的正方形单元(例如1 km×1 km)，则两者将更为一致.

4 算例

4.1 虚拟事件

4.1.1 速度模型

虚拟事件以云南地区为背景.云南是我国中强地震多发地区，为此在该区开展了大量深部结构探测活动(Kan et al., 1986; 王椿镛等，2002).根据深地震测深资料，获得了多条高分辨率地壳速度结构剖面(白志明和王椿镛, 2003; Zhang et al., 2011; Teng et al., 2013).对其中的遮放—宾川速度剖面(白志明和王椿镛，2004)略做平滑处理，得到如图3所示模型，S波与P波速度之比vS∶vP设为常数1∶1.73.可以看到，该模型在深度上和横向上都存在较强的非均匀性.将模型剖分成1km×1km的正方形单元，模型单元内速度为常数.在地表布设9个地震台站Ri(i=1, 2, 3,…,9)，其位置如表1所示.假设在点x0(130.5 km, -27.5 km)处发生地震，发震时间t0=0 s.震源至地震台站的P和S波到时与射线路径利用改进最小走时树算法(Zhao et al., 2004)计算，射线路径如图3中黑线所示.

对图3中事件，利用改进方法计算其分别以到时差和到时约束的两种震源轨迹.到时差约束的震源轨迹每条仅涉及两个观测到时，具有较强的独立性，研究得较多(白玲等，2003；廉超等，2006；Zhao and Ding, 2007, 2009; 赵爱华等，2008；Theunissen et al., 2012)；到时约束的震源轨迹不仅与每条对应的到时有关，而且还与构建发震时间场的到时有关，目前研究得还较少.因此，对于前种轨迹仅考虑全部台站观测、速度模型与到时均准确的情况；对于后种轨迹则考虑不同台站观测(包括全部台、稀疏台、近台、远台和单侧台)、速度模型与到时均准确以及全部台站观测、速度模型准确、到时有扰动的情况.震源轨迹计算参数RFLRP=0.1 s,RFL=0.2 s,Ltwig=5.

图3 复杂模型(修改自白志明等，2004) 震源(红色十字)至台站(黑色倒三角形)的联线为地震波传播路径.Fig.3 A complex model (from Bai et al., 2004)The black lines are ray paths of seismic waves from the hypocenter (cross) to stations (inverse triangles).

表1 复杂速度模型中地震台站位置Table 1 Positions of the seismic receivers in the complex model

4.1.2 到时差约束的震源轨迹

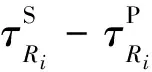
当仅有部分台站观测时，例如只保留台站R5～R9，由于较多分布方位缺失，上述两类震源轨迹各自对震源的约束大大减弱.不过由于这两类轨迹在分布方位上存在互补性，将两者结合可在一定程度上弥补观测上的不足.当速度模型或到时存在扰动时，可以预计轨迹将不会恰好交汇于一点而是交汇成一个区域(参见赵爱华等，2008).

4.1.3 到时约束的震源轨迹

全部台站P波到时约束的9条震源轨迹显示在图5a中.和到时差约束的震源轨迹(图4a)相比，到时约束的震源轨迹在震源处的方位分布不是很全面和均匀，大部分轨迹靠近垂直方向分布，不过有两条轨迹与垂直方向的夹角较大，因此仍能较好地约束震源位置.当以全部台站P波和S波到时构建发震时间场时，P波(蓝线)、S波(绿线)到时约束的震源轨迹如图5b所示.增加S波到时信息后，震源轨迹与之前的方位分布非常相似，仅略有改善，不过有更多轨迹约束震源，可更好地减少抗随机干扰的影响.

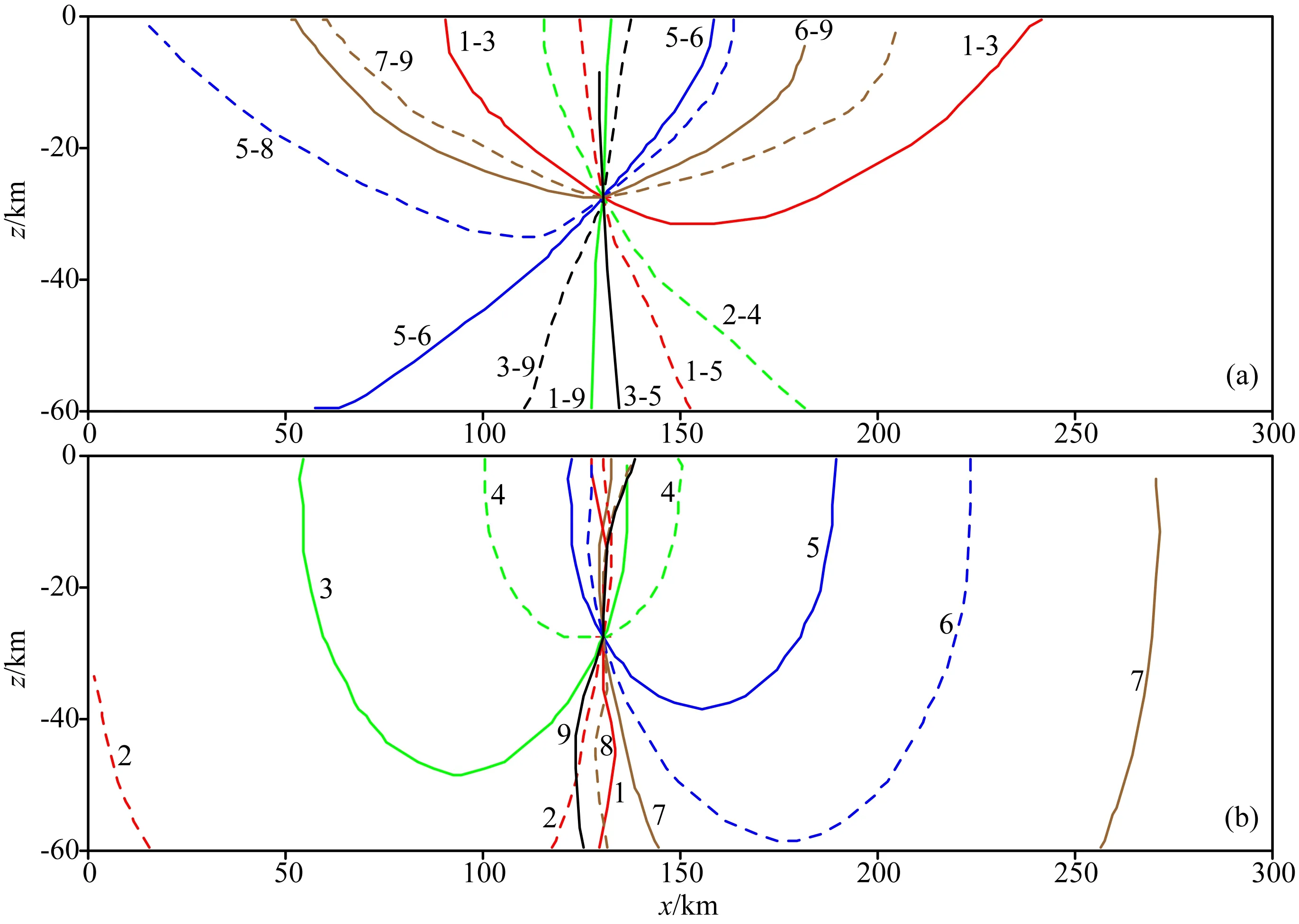
图4 复杂速度模型中事件以到时差约束的震源轨迹(a) 不同台站P波到时差约束的震源轨迹; (b) 相同台站P波与S波到时差约束的震源轨迹.Fig.4 Hypocentral loci constrained with arrival time differences for the event in the complex model(a) Focal loci constrained with arrival time differences between P waves at different stations; (b) Those with ones between P and S waves at the same stations.

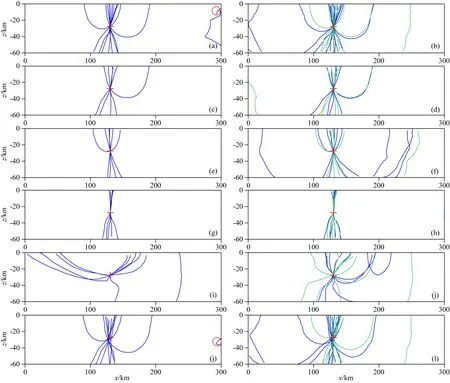
图5 复杂速度模型中事件以到时约束的震源轨迹(a)和(b)所有台; (c)和(d)稀疏台; (e)和(f) 近台; (g)和(h) 远台; (i)和(j) 右侧台; (k)和(l)扰动到时. 左边图仅使用P波到时; 右边图使用P和S波两种到时，其中蓝线和红线分别对应P波、S波. 红色“+”为震源位置.Fig.5 Hypocentral loci constrained with arrival times for the event in the complex model(a) and (b) all stations; (c) and (d) sparse stations; (e) and (f) near stations; (g) and (h) far stations; (i) and (j) right-side stations; (k) and (l) noisy arrival times. Focal loci in the left panels are constrained with only P- wave arrival times; those in the right ones with both P- and S- wave data, where the blue and green lines respond to P and S waves, respectively. The red “+” indicate the true hypocenter.

在全部台站情况中，台站间距为30或20 km, 而实际台站间距通常要比之大1倍或更多.为此，仅保留序号为奇数的台站R2i-1(i=1, 2, 3，…，5).稀疏台P波及其与S波到时约束的震源轨迹分别显示在图5(c，d)中.可以看出，当台站间距增大后，震源轨迹在震源处的方位分布范围略有减小，但仍能较好地约束震源位置.与之相似的是近台(R2—R6)约束的震源轨迹(5(e，f)).当仅有远台(R1、R2、R7、R8和R9)时，无论单独P波还是其与S波约束的震源轨迹(图5(g，h))在震源处都近垂直分布，难以约束震源深度.

在定位实践中，事件常常位于地震台网之外.为模拟该种情形，仅保留右侧5个台站R5～R9.P波到时约束的震源轨迹如图5i所示.震源轨迹在震源处以水平为主的方位分布，似乎显示可很好地约束震源深度，而对震中位置约束较弱.增加S波到时信息后，震源轨迹在震源处的方位分布变得不仅全面而且均匀，如图5j所示，这与前几种情况显著不同.这表明，在局部观测条件下对地震进行定位时，联合使用P波和S波到时尤其重要.此外，还可以看到震源轨迹除了在震源处交会外，还有几条轨迹在震源的右上地方交会.这意味着总的到时残差函数存在局部极小值，当以盖革法(以总的到时残差为目标函数)定位时，所给初始震源参数须离真值较近.

震相到时受环境、仪器及人为等因素影响总会或多或少存在误差.为考察到时拾取误差对震源轨迹分布的影响，对全部9个台站的理论到时加幅度为±0.5 s的随机扰动(扰动利用FORTRAN90编译器中的随机函数生成)，P、S波的均方到时扰动量分别为0.356 s和0.321 s.P波到时单独约束、P和S波到时联合约束的震源轨迹分别如图5(k，l)所示.可以看出，当观测到时有误差时，震源轨迹不再交会于震源点，而是交会成一个小的区域.和图5k相比，图5l中震源轨迹交会最密集的点更接近实际震源位置.

4.2 真实事件

4.2.1 事件与速度模型

真实事件来自华北地区.华北地区是我国重点地震监测地区，该区地震台站分布密集且较均匀.为在二维剖面上较好地考察震源轨迹分布，事件震中和台站应成线分布.2012年8月26日(北京时间)发生在华北东部的ML4.2级地震较符合这一要求.据北京数字遥测地震台网(北京台网)测定，该事件震中位于117.42°E、39.61°N, 深13 km, 发震时间为7时13分34.3秒.图6显示了事件震中及其周围台站.需要指出的是，在更大的范围内还有更多观测台站.可以看出，该事件不仅有良好的方位观测覆盖，而且有近台控制(CAD台的震中距仅3 km).基于台网分布分析(Bondár et al., 2004), 可认为北京台网的定位结果是可靠的.在由“重复地震”得到的北京台网定位精度图(蒋长胜等，2008)上，震中处的定位精度可达2km或更高.北京台网基于走时表、采用单纯形方法定位，观测走时及走时残差列于表2中.由表2中较小的走时残差也可推断北京台网的定位结果较为可靠.此外，值得一提的是北京台网和中国地震台网中心的定位结果相当一致: 震中相差不到1.5 km、震源深度相差3 km，发震时间相差0.1 s.这样，可以认为事件震中和台站EWZ、CAD和XAZ基本位于直线AB上.

华北地区地壳三维速度结构有较多的研究成果，例如嘉世旭等(2005)、齐诚等(2006)、于湘伟等(2010).根据已有结果可知，沿直线AB方向，介质横向非均匀性较弱.另外，地震台网采用1D模型进行定位仍较普遍.为此，本文仍采用1D模型.模型由三层介质组成，从上至下各层厚度(H)、P波速度(vP)和S波速度(vS)为：H1=5 km、vP1=5.0 km·s-1、vS1=2.6 km·s-1;H2=15 km、vP2=6.1 km·s-1、vS2=3.5 km·s-1;H3=15 km、vP3=6.8 km·s-1、vS3=3.9 km·s-1.模型参照华北东部模型(滕吉文等，1979)、根据观测走时构建.模型使用0.1 km×0.1 km网格剖分.以北京台网测定的震源位置为标准，本文模型的走时残差如表2所示.由走时残差来看，所构建的模型是可以接受的.

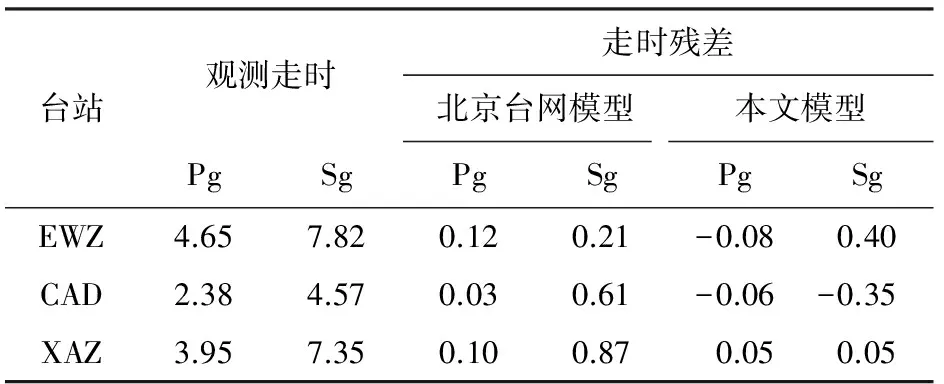
表2 真实事件的观测走时及走时残差(单位：s)Table 2 Observed traveltimes and traveltime residuals for the real (unit: s)

图6 真实事件的震中(红色“+”)及观测台站(实三角形)Fig.6 Epicenter (red “+”) of a real event and the seismic stations (solid triangles)

4.2.2 震源轨迹

三个台站EWZ、CAD和XAZ两两组合、P波到时差约束的震源轨迹如图7a所示.不同轨迹以不同颜色表示.可以看出，P波到时差约束的震源轨迹近似为双曲线；三条轨迹较好地交汇于一点.和北京台网确定的震源位置(图中红色“+”)相比，交汇点略向右下偏.同一台站P、S波到时差约束的震源轨迹显示在图7b中.从左至右三个台站对应的轨迹分别以红、绿和蓝色标示.不难看出，尽管存在纵向非均匀性，轨迹仍大体为圆形，但交汇得不是很集中，特别是EWZ台轨迹(红色)偏离台网所定震源较远，这可能主要与该台Sg震相走时残差较大有关.

图7 真实事件的震源轨迹(a) P波到时差约束； (b) P-S波到时差约束； (c) P波到时约束； (d) P和S波到时约束. 红色“+”为北京地震台网确定的震源位置.Fig.7 Hypocentral loci of the real event(a) Constraint of arrival time differences between P waves; (b) Constraint of those between P and S waves; (c) Constraint of P-wave arrival times; (d) Constraint of P- and S- wave ones. The red signs of “+” indicate the hypocenter located by Beijing seismic network.

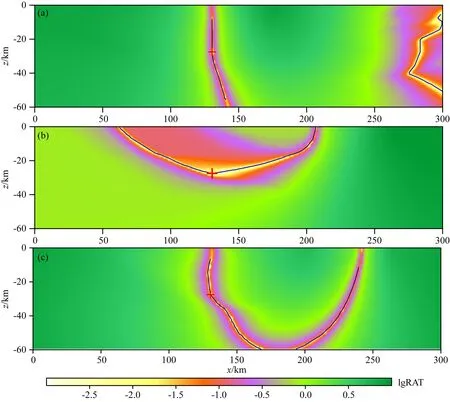
图8 复杂模型中事件到时残差(RAT)场中的震源轨迹(a)台站R6的P波到时约束的震源轨迹, 发震时刻场使用所有台站的P波到时构建; (b)和(c) 台站R9的P波到时约束的震源轨迹, 其发震时间场分别使用台站R7—R9的P波到时单独、P波和S波到时共同构建. 红色“+”为震源位置.Fig.8 Hypocentral loci in the fields of RAT (residual of arrival time) for the event in the complex model(a) The hypocentral locus is constrained with the P wave arrival time at station R6, and its origin time field is constructed with P-wave data from all the nine stations. (b) and (c) The hypocentral loci are constrained with the same P-wave arrival time at station R9, but their origin time fields are constructed with only P-wave, and both P-and S-wave data from stations R7—R9, respectively. The red “+” indicate the true hypocenter.

EWZ台和XAZ台轨迹存在中断现象(中断位于第一界面处)，这源于在两个台站处激发的地震波沿界面折射滑行，走时在界面处发生跃变.

P波到时约束的震源轨迹显示在图7c中.红、绿和蓝色轨迹分别对应台站EWZ、CAD和XAZ.轨迹2条似双曲线、1条接近圆形.3条轨迹不仅较好地交汇于一点，而且方位分布较为全面，特别是对震源深度有很好地约束.据此推断，实际震源可能要比台网所定位置略深并偏向东北.P、S波到时联合约束的震源轨迹如图7d所示.红、绿和蓝色轨迹分别对应台站EWZ、CAD和XAZ，实线和虚线分别对应P、S波.和图7b类似，轨迹交汇得也不集中，但交汇区包含了台网所定震源位置.和单纯的P波相比，P、S波约束的震源轨迹交汇得较分散，这可能与S波的速度模型及/或拾取的震相到时误差较大有关.

5 讨论

5.1 震源轨迹稳定性

复杂模型的算例显示，从震源轨迹的方位分布来看，远台似乎有时更能约束震源深度(见图4a和图5i)，与常识明显不符.实际上，震源轨迹对震源位置的约束，不仅要看轨迹在震源处的分布方位，而且还要考虑其稳定性.若将震源轨迹所在的残差场看作地形图，则震源轨迹位于山谷中.山谷越窄陡，轨迹越稳定；山谷越宽缓，轨迹稳定性越差.

图8a显示了图5a中标有红圈的震源轨迹的到时残差场，该轨迹对应台站R6.可以看出，该轨迹由左、右两段组成.和左段相比，右段残差较小(例如小于0.1 s)的条带要宽得多，稳定性较弱.残差场中蓝线为RFLRP=0.01 s时计算的震源轨迹.和图5a相比，红圈标示部位的轨迹略有不同，在形态上更接近实际.当观测到时有误差时，稳定性较弱的右段形状发生很大变化，见图5k红圈标示部分.与之相比，稳定性强的左段形状改变较小.这表明，稳定性弱的震源轨迹易受干扰影响.

为更清楚地揭示远台对震源深度的实际约束能力，考虑台站R7、R8和R9到时约束的震源轨迹.图8b显示了发震时间场以P波到时构建，台站R9处P波到时约束的震源轨迹及其所在的残差场.震源轨迹尽管在震源处近水平分布，但由于稳定性差，特别是在震源附近，即使很小的干扰，其位置和形状都可能发生很大变化，因此对震源深度的实际约束并不是很强.当构建发震时间场时增加S波到时信息，同一到时对应的震源轨迹则稳定得多，如图8c所示.台站R7和R8对应的轨迹情况与之类似.因此，增加使用S波到时对震源位置约束的强化，不仅在于震源轨迹方位分布的改善，还在于轨迹稳定性的提高.

5.2 震源轨迹计算参数的选取

震源轨迹代表点的选取参数RFLRP控制轨迹代表点选取范围.为保证轨迹完整性，初选点应包含轨迹各段端点所在模型单元的节点，即这些节点的最大残差值为RFLRP的下限，通常地震波速度越小、模型单元尺寸越大，该值越大.另一方面，由于是通过不断“削去”初选点集合外皮、保留其核心作为震源轨迹代表点，因此RFLRP不能大到初选点组成的连通区域有多个“核”，即每个连通区域应仅包含1段震源轨迹.实际上，满足上述要求的RFLRP取值范围是较宽的.图9显示了均匀模型算例中P波到时约束的震源轨迹其初选(虚线)、实际(实线)代表点占所有模型节点百分比随参数RFLRP的变化，RFLRP的步长取0.005s.可以看出，RFLRP在约0.03～0.5s的较宽范围内，震源轨迹代表点的选取结果都很稳定，这种稳定性意味着参数RFLRP不需要随震源轨迹形态变化而调整，因而有利于大批量数据的自动处理.在保证轨迹完整性的前提下，RFLRP应尽量取小，这样不仅可减少计算量，而且对于稳定性较弱的震源轨迹，可保证选取的轨迹代表点有较好的代表性.

图9 图1c中震源轨迹代表点(实线)及其初选点(虚线)百分比Fig.9 Percentages of primary (dashed line) and final (solid line) reference points for the focal locus in Fig.1c

射线路径的计算参数RFL控制射线路径的追踪区域.为保证震源轨迹的完整性、且不出现虚假轨迹，残差小于RFL的连通区域应完整包含且仅包含1段轨迹，即轨迹所经过模型单元节点的残差最大值为RFL的下限，但RFL不能大到有连通区域包含多于1段震源轨迹.对于只有1段的震源轨迹，RFL的上限可取至包括整个模型空间；对于多段的震源轨迹，RFL的取值范围通常也是比较宽的，以图8a为例，RFL在0.1～0.5s范围内取值均可.对于较小的RFL，射线追踪区域为1个或多个狭窄条带，这些条带占模型区域的比例很小，因之震源轨迹计算较快.

震源轨迹的修饰参数Ltwig控制所要去掉的射线路径的长度，其取值大小与选取的轨迹代表点有关.当代表点均沿轨迹分布时，不再分叉的射线路径较短，Ltwig可取得较小.对于稳定性较弱的震源轨迹，当参数RFLRP取得较大时，选取的轨迹代表点会包含代表性较差的点，此时Ltwig应取得大些以去掉距轨迹较远点的射线路径.

5.3 算法到三维介质的扩展性

地震定位是个三维问题.在三维残差场中，震源轨迹所经过模型单元的节点残差局部最小，这些节点位于残差较小区域的中心，更类似于实际的果中之核.因此，选取轨迹代表点的“削皮”算法同样适用于三维模型，只是在消除多余代表点的细节上会略有不同.射线路径的计算基于最小走时树算法，该算法对于二维和三维模型，具有相同的框架.在三维模型中，计算的射线路径同样具有树状结构，因此仍然可以采用类似修剪树枝的方法来修饰震源轨迹使之精细.这样，利用三维最小走时树算法(Klimes and Kvasnicka, 1994; 王辉等，2000；赵爱华和张中杰, 2004)可较容易地将本文提出的改进算法推广到三维模型.和二维模型相比，三维模型震源轨迹的计算量要大得多，这主要是计算三维走时场较为费时，不过这部分仅需计算一次.因此，对于速度结构稳定的地区，当处理同一地震台网记录的多个事件时，震源轨迹的计算效率还是较高的.

6 结论

本文提出的计算震源轨迹的改进方法不仅保持了原方法适于复杂速度模型的优点，而且可计算任意多段的震源轨迹，能较好地兼顾计算轨迹的完整性与精细性.射线追踪仅限于残差较小的区域，显著减少了计算量.震源轨迹计算参数设置简单，不需要随轨迹形态分布反复调整，有利于大批量数据的自动处理.改进方法易于扩展到三维介质模型.由于相对费时的走时场计算仅需一次，因此对于速度结构稳定地区、同一台网记录的多个地震，震源轨迹计算效率较高.

数值模型计算表明：到时差和到时约束的震源轨迹具有不同的形态分布，即使介质均匀后者也较复杂；震源轨迹对震源位置的约束，不仅要看轨迹在震源处的方位分布，而且要考虑轨迹的稳定性；近台到时对震源深度有较强的约束；在速度模型及震相到时较准的情况下增加S波到时可改善对震源位置的约束，对于台网外地震尤为显著；使用多条轨迹，有助于减少随机因素对定位的影响.

致谢 中国科学院地质与地球物理研究所张中杰研究员对本项工作给予了支持和指导；真实事件数据来自北京数字遥测地震台网，田宝峰博士和房立华博士给予了热情帮助.作者在此表示衷心感谢.

Bai L, Zhang T Z, Zhang H Z. 2003. Multiplet relative location and wave correlation correction and their application.ActaSeismologicaSinica(in Chinese), 25(6): 591-600.Bai Z M, Wang C Y. 2003. Tomographic investigation of the upper crustal structure and seismotectonic environments in Yunnan Province.ActaSeismologicaSinica(in Chinese), 25(2): 117-127.

Bai Z M, Wang C Y. 2004. Tomography research of the Zhefang-Binchuan and Menglian-Malong wide-angle seismic profiles in Yunnan province.ChineseJ.Geophys. (in Chinese), 47(2): 257-267.

Billings S D, Sambridge M S, Kennett B L N. 1994. Errors in hypocenter location: picking, model, and magnitude dependence.Bull.Seism.Soc.Am., 84(6): 1978-1990.Bondár I, Myers S C, Engdahl E R, et al. 2004. Epicentre accuracy based on seismic network criteria.Geophys.J.Int., 156(3): 483-496.

Cai M J, Shan X M, Xu Y, et al. 2004. Review of earthquake-locating methods from error.JournalofSeismologicalResearch(in Chinese), 27(4): 314-317.

Cao S H, Greenhalgh S. 1993. Calculation of the seismic first-break time field and its ray path distribution using a minimum traveltime tree algorithm.Geophys.J.Int., 114(3): 593-600.

Chen H, Chiu J M, Pujol J, et al. 2006. A simple algorithm for local earthquake location using 3DVPandVSModels: test examples in the central United States and in central eastern Taiwan.Bull.Seismol.Soc.Am., 96(1): 288-305.

Chen Y T. 2009. Earthquake prediction: Retrospect and prospect. Sci.ChinaSer.D-EarthSci. (in Chinese), 39(12): 1633-1658.Ding Z F, He Z Q, Sun W G, et al. 1999. 3-D crust and upper mantle velocity structure in eastern Tibetan plateau and its surrounding areas.ChineseJ.Geophys. (in Chinese), 42(2): 197-205.

Font Y, Kao H, Lallemand S et al. 2004. Hypocentre determination offshore of eastern Taiwan using the Maximum Intersection method.Geophys.J.Int., 158: 655-675.

Geiger L. 1912. Probability method for the determination of earthquake epicenters from the arrival time only.Bull.St.LouisUniv., 8: 60-71.

Jia S X, Qi C, Wang F Y, et al. 2005. Three-dimensional crustal gridded structure of the Capital area.ChineseJ.Geophys. (in Chinese), 48(6): 1316-1324.

Jiang C S, Wu Z L, Li Y T. 2008. Estimating the location accuracy of the Beijing Capital Digital Seismograph Network using repeating events.ChineseJ.Geophys. (in Chinese), 51(3): 817-827.

Kan R J, Hu H X, Zeng R S, et al. 1986. Crustal structure of Yunnan province, People′s Republic of China, from seismic refraction profiles.Science, 234(4775): 433-437.

Lian C, Li S L, Dong M, et al. 2006. Method of spherical surface shearing in earthquake location.JournalofGeodesyandGeodynamics(in Chinese), 26(2): 99-103.

Meng Y M, Zhao Y, Wang B. 2001. The analysis on deviation of rapid location by China Seismic observational Network.Earthquake(in Chinese), 21(3): 65-69.

Moser T J. 1991. Shortest path calculation of seismic rays.Geophysics, 56(1): 59-67.

Nakanishi I, Yamaguchi K. 1986. A numerical experiment on nonlinear image reconstruction from first-arrival times for two-dimensional island arc structure.J.Phys.Earth, 34(2): 195-201.

Pujol J. 2004. Earthquake location tutorial: graphical approach and approximate epicentral location techniques.Seismol.Res.Lett., 75(1): 63-74.Qi C, Zhao D P, Chen Y, et al. 2006. 3-D P and S wave velocity structures and their relationship to strong earthquakes in the Chinese capital region.ChineseJ.Geophys. (in Chinese), 49(3): 805-815.Richards P G, Waldhauser F, Schaff D, et al. 2006. The applicability of modern methods of earthquake location.PureandAppliedGeophysics, 163(2-3): 351-372.

Shearer P M. 1997. Improving local earthquake locations using the L1 norm and waveform cross correlation: Application to the Whittier Narrows, California, aftershock sequence.J.Geophys.Res., 102(B4): 8269-8283.Song R, Gu X H, Wang Y L, et al. 2001. The software system for real-time processing and large earthquake rapid determination of NCDSN.Earthquake(in Chinese), 21(4): 47-59.

Teng J W, Yao H, Zhou H N. 1979. Crustal structure in the Beijing-Tianjin-Tangshan-Zhangjiakou region.ActaGeophysicaSinica(in Chinese), 22(3): 218-236.

Teng J W, Zhang Z J, Zhang X K, et al. 2013. Investigation of the Moho discontinuity beneath the Chinese mainland using deep seismic sounding profiles.Tectonophysics, 609: 202-216.

Theunissen T, Font Y, Lallemand S, et al. 2012. Improvements of the Maximum Intersection Method for 3D Absolute Earthquake Locations.Bull.Seismol.Soc.Am., 102(4): 1764-1785.

Tian Y, Chen X F. 2002. Review of seismic location study.ProgressinGeophysics(in Chinese), 17(1): 147-155.

Udías A. 1999. Principles of Seismology. Cambridge: Cambridge University Press.Waldhauser F, Ellsworth W L. 2000. A double-difference earthquake location algorithm: method and application to the northern Hayward fault, California.Bull.Seismol.Soc.Am., 90(6): 1353-1368.

Wang C Y, Mooney W D, Wang X L, et al. 2002. Study on 3-D velocity structure of crust and upper mantle in Sichuan-Yunnan Region, China.ActaSeismologicaSinica(in Chinese), 24(1): 1-16.

Wang H, Chang X. 2000. 3-D ray tracing method based on graphic structure.ChineseJ.Geophys. (in Chinese), 43(4): 534-541.

Xu L S, Du H L, Yan C, et al. 2013a. A method for determination of earthquake hypocentroid: time-reversal imaging technique I- Principle and numerical tests.ChineseJ.Geophys. (in Chinese), 56(4): 1190-1206, doi: 10.6038/cjg20130414.Xu L S, Yan C, Zhang X, et al. 2013b. A method for determination of earthquake hypocentroid: time-reversal imaging technique II—An examination based on people-made earthquakes.ChineseJ.Geophys. (in Chinese), 56(12): 4009-4027, doi: 10.6038/cjg20131207.

Yang W D, Jin X, Li S Y, et al. 2005. Study of seismic location methods.EarthquakeEngineeringandEngineeringVibration(in Chinese), 25(1): 14-20.

Yu X W, Chen Y T, Zhang H. 2010. Three-dimensional crustal P-wave velocity structure and seismicity analysis in Beijing-Tianjin-Tangshan Region.ChineseJ.Geophys. (in Chinese), 53(8): 1817-1828, doi: 10.3969/j.issn.0001-5733.2010.08.007.

Zeng R S. 1991. The problems of lithospheric structure and geodynamics.AdvanceinEarthSciences(in Chinese), 6(2):1-10.

Zhang Z J, Yang L Q, Teng J W, et al. 2011. An overview of the earth crust under China.Earth-ScienceReviews, 104(1-3): 143-166.

Zhao A H, Zhang Z J, Peng S P. 2003. Fast ray tracing method for converted waves in complex media.JournalofChinaUniversityofMining&Technology(in Chinese), 32(5): 513-516.

Zhao A H, Zhang Z J. 2004. Fast calculation of converted wave traveltime in 3-D complex media.ChineseJ.Geophys. (in Chinese), 47(4): 702-707.Zhao A H, Zhang Z J, Teng J W. 2004. Minimum travel time tree algorithm for seismic ray tracing: improvement in efficiency.J.Geophy.Eng., 1(4): 245-251.

Zhao A H, Ding Z F. 2007. An intersection method for locating earthquakes in complex velocity models.AppliedGeophysics, 4(4): 294-300.

Zhao A H, Ding Z F, Sun W G, et al. 2008. Calculation of focal loci for earthquake location in complex media.ChineseJ.Geophys. (in Chinese), 51(4): 1188-1195.

Zhao A H, Ding Z F. 2009. Earthquake location in transversely isotropic media with a tilted symmetry axis.J.Seismol., 13(2): 301-311.

Zhao A H. 2104. Hypocentral loci in earthquake location under the constraint of arrival time residual norm. ∥ Chen Y T, Jin Z M, Shi Y L, et al. A Study of Interior Physics and Dynamics of Continental China — in Honor of Academician Teng Jiwen′s 60th Anniversary of being Engaged in Geophysical Research (in Chinese). Beijing: Science Press, 265-280.Zhou H W. 1994. Rapid three-dimensional hypocentral determination using a master station method.J.Geophys.Res., 99(B8): 15439-15455.Zhou J C, Zhao A H. 2012. An intersection method for locating earthquakes in 3-D complex velocity models.ChineseJ.Geophys. (in Chinese), 55(10): 3347-3354, doi: 10.6038/j.issn.0001-5733.2012.10.017.

附中文参考文献

白玲, 张天中, 张宏智. 2003. 多重相对定位法和波形相关校正及其应用. 地震学报, 25(6): 591-600.

白志明, 王椿镛. 2003. 云南地区上部地壳结构和地震构造环境的层析成像研究. 地震学报, 25(2): 117-127.

白志明, 王椿镛. 2004. 云南遮放—宾川和孟连—马龙宽角地震剖面的层析成像研究. 地球物理学报, 47(2): 257-267.

蔡明军, 山秀明, 徐彦等. 2004. 从误差观点综述分析地震定位方法. 地震研究, 27(4): 314-317.

陈运泰. 2009. 地震预测: 回顾与展望. 中国科学D辑: 地球科学, 39 (12): 1633-1658.

丁志峰, 何正勤, 孙为国等. 1999. 青藏高原东部及其边缘地区的地壳上地幔三维速度结构. 地球物理学报, 42(2): 197-205.

嘉世旭, 齐诚, 王夫运等. 2005. 首都圈地壳网格化三维结构. 地球物理学报, 48(6): 1316-1324.

蒋长胜, 吴忠良, 李宇彤. 2008. 首都圈地区“重复地震”及其在区域地震台网定位精度评价中的应用. 地球物理学报, 51(3): 817-827.

廉超, 李胜乐, 董曼等. 2006. 球面交切法地震定位. 大地测量与地球动力学, 26(2): 99-103.

孟玉梅, 赵永, 王斌. 2001. 中国地震观测台网地震速报定位偏差的分析. 地震, 21(3): 65-69.

齐诚, 赵大鹏, 陈颙等. 2006. 首都圈地区地壳P波和S波三维速度结构及其与大地震的关系. 地球物理学报, 49(3): 805-815.

宋锐, 顾小红, 王永力等. 2001. 国家数字地震台网中心实时处理及大地震速报软件系统. 地震, 21(4): 47-59.

滕吉文, 姚虹, 周海南. 1979. 北京、天津、唐山和张家口地区的地壳结构. 地球物理学报, 22(3): 218-236.

田玥, 陈晓非. 2002. 地震定位研究综述. 地球物理学进展, 17(1): 147-155.

王椿镛, Mooney W D, 王溪莉等. 2002. 川滇地区地壳上地幔三维速度结构研究. 地震学报, 24(1): 1-16.

王辉, 常旭. 2000. 基于图形结构的三维射线追踪方法. 地球物理学报, 43(4): 534-541.

许力生, 杜海林, 严川等. 2013a. 一种确定震源中心的方法: 逆时成像技术(一)—原理与数值实验. 地球物理学报, 56(4): 1190-1206, doi: 10.6038/cjg20130414.

许力生, 严川, 张旭等. 2013b. 一种确定震源中心的方法: 逆时成像技术(二)—基于人工地震的检验. 地球物理学报, 56(12):4009-4027, doi: 10.6038/cjg20131207.

杨文东, 金星, 李山有等. 2005. 地震定位研究及应用综述. 地震工程与工程振动, 25(1): 14-20.

于湘伟, 陈运泰, 张怀. 2010. 京津唐地区地壳三维P波速度结构与地震活动性分析. 地球物理学报, 53(8): 1817-1828, doi: 10.3969/j.issn.0001-5733.2010.08.007.

曾融生. 1991. 大陆岩石圈构造与地球动力学. 地球科学进展, 6(2): 1-10.

赵爱华, 张中杰, 彭苏萍. 2003. 复杂地质模型转换波快速射线追踪方法. 中国矿业大学学报, 32(5): 513-516.

赵爱华, 张中杰. 2004. 三维复杂介质中转换波走时快速计算. 地球物理学报, 47(4): 702-707.

赵爱华, 丁志峰, 孙为国等. 2008. 复杂介质地震定位中震源轨迹的计算. 地球物理学报, 51(4): 1188-1195.

赵爱华. 2014. 地震定位中到时残差范数下的震源轨迹. ∥ 陈运泰, 金振民, 石耀霖等. 中国大陆地球内部物理学与动力学研究—庆贺滕吉文院士从事地球物理学研究60周年. 北京: 科学出版社, 265-280.

周建超, 赵爱华. 2012. 三维复杂速度模型的交切法地震定位. 地球物理学报, 55(10): 3347-3354, doi: 10.6038/j.issn.0001-5733.2012.10.017.

(本文编辑 汪海英)

Improvement of the ray-tracing based method calculating hypocentral loci for earthquake location

ZHAO Ai-Hua1, DING Zhi-Feng1, BAI Zhi-Ming2

1InstituteofGeophysics,ChinaEarthquakeAdministration,Beijing100081,China2InstituteofGeologyandGeophysics,ChineseAcademyofSciences,Beijing100029,China

Hypocentral loci are very useful for reliable and visual earthquake location, but they can hardly be analytically expressed when the velocity model is complex. There is a ray-tracing based numerical method to calculate them, in which a focal locus is represented in terms of ray paths from the minimum point (namely initial point) to low residual points (referred as hypocentral locus reference points, HLRPs) in its residual field. It has no restrictions on the complexity of the velocity model and can produce quite fine results. However, this method is incapable of addressing multi-segment loci and inadequate for processing large quantity of data. Additionally, it is rather laborious and difficult to set its controlling parameters for obtaining both fine and complete hypocentral loci. This paper presents an improvement of the ray-tracing based method.The method for calculating hypocentral loci is based on the minimum traveltime tree algorithm for tracing rays. It consists of three steps: (1) HLRPs are selected from nodes of the model cells that the hypocentral locus runs through by means of a so-called peeling method. (2) The calculation domain of a hypocentral locus is defined as such a low residual area that its connected regions each include one segment of the locus and then all the focal locus segments are respectively calculated with the minimum traveltime tree algorithm for tracing rays by repeatedly assigning the minimal point among those HLRPs that have not been traced as an initial point. (3) Short ray paths without branching are removed to make the calculated locus finer.The improved method is applied to a virtual seismic event and a real earthquake. The virtual event takes place in a 300 km×60 km complex velocity model with a background of Yunnan area. It is covered well by 9 seismic stations. The real earthquake occurred in North China and its epicenter and three seismic stations are located in an approximately straight line. Considering the lateral heterogeneity along the line is weak, a horizontally homogeneous crustal model is employed for calculating theoretical travel times. The differences between the observed and the calculated traveltimes are no more than 0.1 s for P waves and 0.4 s for S waves. For the two events, we calculate their hypocentral loci constrained with arrival times and those with arrival time differences when only P waves are used and both P and S waves are used. As for the arrival time constrained hypocentral loci of the virtual event, we investigate them in six different cases: (a) all stations, (b) sparse stations; (c) near stations; (d) far stations; (e) right-side stations; and (f) noisy arrival times. The numerical tests show that one-segment and multi-segment hypocentral loci are calculated correctly and their intactness is maintained well. For the same event, resultant fine hypocentral loci intersect exactly at the hypocenter when the velocity model and the observed arrival times are accurate. The parameters controlling the quality of outputting results can be chosen within a quite wide range and require little adjusting once they are set properly. Hypocentral loci associated with near stations have strong constraints on hypocenters. Additional use of S-wave data can improve the azimuth distribution and the stability of hypocentral loci.The improved method is capable of efficiently calculating hypocentral loci with good completeness and fineness for earthquakes in a complex model. Arrival times from near stations are critically important for determining hypocenters. S-wave data are helpful in strengthening the constraint on hypocenters, especially when the observation is incomplete.

Earthquake location; Hypocentral locus; Ray tracing; Minimum traveltime tree algorithm; Peeling method

赵爱华, 丁志峰, 白志明. 2015. 基于射线追踪技术计算地震定位中震源轨迹的改进方法.地球物理学报，58(9):3272-3285,

10.6038/cjg20150922.

Zhao A H, Ding Z F, Bai Z M. 2015. Improvement of the ray-tracing based method calculating hypocentral loci for earthquake location.ChineseJ.Geophys. (in Chinese),58(9):3272-3285,doi:10.6038/cjg20150922.

10.6038/cjg20150922

P315

2014-09-17，2015-08-26收修定稿

国家自然科学基金项目(41374098,40974050),中央国家级公益事业单位基本科研业务费专项(DQJB11C03)资助.

赵爱华，男，1970年出生，研究员，2001年在中国科学院地质与地球物理研究所获理学博士学位，主要从事复杂介质射线追踪方法及其应用研究.E-mail:ahzhao123@yahoo.com