基于自适应优化有限差分方法的全波VSP逆时偏移

蔡晓慧， 刘洋*， 王建民， 王维红， 任志明

1 中国石油大学(北京)油气资源与探测国家重点实验室， 北京 102249 2 中国石油大学(北京)CNPC物探重点实验室， 北京 102249 3 大庆油田有限责任公司勘探开发研究院， 大庆 163318



基于自适应优化有限差分方法的全波VSP逆时偏移

蔡晓慧1,2， 刘洋1,2*， 王建民3， 王维红3， 任志明1,2

1 中国石油大学(北京)油气资源与探测国家重点实验室， 北京 102249 2 中国石油大学(北京)CNPC物探重点实验室， 北京 102249 3 大庆油田有限责任公司勘探开发研究院， 大庆 163318

与地面地震资料相比，VSP资料具有分辨率高、环境噪声小及能更好地反映井旁信息等优点.常规VSP偏移主要对上行反射波进行成像，存在照明度低、成像范围受限等问题.为了增加照明度、拓宽成像范围、提高成像精度，本文采用直达波除外的所有声波波场数据(全波)，包括一次反射波、多次反射波等进行叠前逆时偏移成像.针对逆时偏移中的四个关键问题，即波场延拓、吸收边界条件、成像条件及低频噪声的压制，本文分别采用自适应变空间差分算子长度的优化有限差分方法(自适应优化有限差分方法)求解二维声波波动方程以实现高精度、高效率的波场延拓，采用混合吸收边界条件压制因计算区域有限所引起的人工边界反射，采用震源归一化零延迟互相关成像条件进行成像，采用拉普拉斯滤波方法压制逆时偏移中产生的低频噪声.本文对VSP模型数据的逆时偏移成像进行了分析，结果表明：自适应优化有限差分方法比传统有限差分方法具有更高的模拟精度与计算效率，适用于VSP逆时偏移成像；全波场VSP逆时偏移成像比上行波VSP逆时偏移的成像范围大、成像效果好；相对于反褶积成像条件，震源归一化零延迟互相关成像条件具有稳定性好、计算效率高等优点.将本文方法应用于某实际VSP资料的逆时偏移成像，进一步验证了本文方法的正确性和有效性.

VSP； 自适应优化有限差分方法； 全波； 逆时偏移

1 引言

近年来，随着VSP技术的发展以及地震勘探对象的日趋复杂，可适应起伏地表、高陡构造、复杂速度区域的VSP成像在实际工业中越来越受重视.因为地面地震资料处理通常不能提供全面、可靠的目标层岩丘下方的构造信息，而VSP技术在查清井旁构造，探明岩丘下方构造，提取纵、横波信息等方面有着重要的作用(Campbell等，2002; Chon等，2003; Hornby等，2006)，因此VSP偏移成像的研究显得十分必要.VSP成像方法主要包括：Harwijanto等(1987)提出的单炮记录反演成像、Nicoletis等(1995)的基于射线理论的偏移成像方法、Xiao和Schuster(2009)的基于格林函数的偏移成像、Chang和McMechan(1986)的基于波动方程的逆时偏移成像方法等.VSP逆时偏移是一种基于全波波动方程的深度域偏移方法，其基本原理是以炮点处震源进行正向延拓，再利用记录的地震波场作为该记录点的边界条件进行逆时延拓，并利用成像条件实现对地下各点的成像.逆时偏移能适应任意复杂速度模型，无倾角限制，理论上可以实现对所有类型波(反射波、绕射波、回转波以及多次反射波等)的成像，而不需要进行上、下行波的分离(Hou and He，1990).20世纪80年代初期，Whitemore(1983)首次提出逆时偏移思想后，叠后逆时偏移得到较快发展.Baysal等(1983)采用伪谱法，Chang等(1986)采用有限差分方法，Loewenthal和Mufti(1983)在空间-频率域分别实现了叠后逆时偏移.随后，叠前逆时偏移开始迅猛发展.Chang和McMechan(1987，1990，1993，1994)应用有限差分方法分别实现了2D和3D的声波、弹性波及各向异性逆时偏移；Causse和Ursin(2000)证明了基于黏弹性介质逆时偏移的有效性；Wu等(1996)实现了3D高阶有限差分逆时偏移.21世纪以来，随着地震勘探对象的复杂化与并行计算机的发展，再一次掀起了逆时偏移研究与应用的热潮.Xu等(2011)实现了角道集逆时偏移；Yan和Liu(2013a)发展了时空域有限差分的声波逆时偏移；Yan和Liu(2013b)、Zhao等(2014)实现了黏滞声波逆时偏移成像；Li等(2014)将最小二乘逆时偏移应用于黏弹介质.除此之外，不少学者对逆时偏移中的难点进行了专门的研究，包括逆时偏移的噪声压制(Yoon et al., 2004; Zhang et al., 2009; Du et al., 2013)、成像方法(Chattopadhyay and Mcmechan，2008)、保幅性(Zhang et al., 2007)、计算量和存储问题(Li et al., 2010; Liu et al., 2010a; Liu et al., 2010b; Wang et al., 2012; Hu et al., 2013)等.针对VSP资料的逆时偏移，Chang等(1986)率先将逆时偏移方法应用到VSP资料；Zhu等(1989)提出了消除内部界面反射波和层间多次波干扰的双程无反射波动方程逆时偏移；Ketil等(1998)和Hokstad等(1988)实现了基于Walkaway VSP资料的弹性波逆时偏移；Xiao和Leaney(2010)实现了基于VSP资料的透射波逆时偏移；Sun和McMechan(2010)提出了一种基于VSP资料的非线性弹性逆时反演；Sun和Sun(2010)应用了伪谱法实现VSP逆时偏移；Sun等(2011)实现了相对保幅的角度域VSP逆时偏移.

VSP逆时偏移中四个关键问题为波场延拓、吸收边界条件、成像条件以及低频噪声的压制.波场延拓的实质是求解波动方程，由于有限差分方法具有计算效率高、精度较高、稳定性较好的优点，因而被广泛应用于求解波动方程.目前主要有两种基于频散关系计算空间导数有限差分系数的方法，一种是基于泰勒级数展开的方法，另一种是基于优化的方法.这两种方法都有一定的优越性和局限性，泰勒级数展开法求解有限差分系数的计算效率高，但是只能在较小的波数或者频率范围内达到较高的精度.对于优化的方法，局部优化方法得到的差分系数难以达到全局优化，而全局优化方法计算效率一般较低，且不一定能得到全局最优解.Liu(2013)提出了一种基于最小二乘的全局优化有限差分方法，这是一种线性求解有限差分系数的方法，计算效率高且能在给定的频带范围内达到较高的精度.本文分析对比了该优化有限差分方法与泰勒级数展开有限差分方法的频散、模拟精度以及VSP逆时偏移结果.模型试算结果表明：在差分算子长度相同的情况下，优化有限差分法比泰勒级数展开有限差分法的模拟精度高，优化有限差分逆时偏移成像结果更准确；在相同模拟精度的前提下，优化有限差分法比泰勒级数展开有限差分法的空间差分算子长度短，即波场延拓的效率高.因此，我们采用优化有限差分法来提高波场延拓的计算效率.为进一步节省计算时间，引入自适应变空间算子长度方案(Liu and Sen，2011)，通过在高速区域采用较短的空间差分算子来提高计算效率.模型试算结果验证了自适应变空间算子长度方案与优化有限差分方法结合(自适应优化有限差分方法)的优越性.本文采用混合吸收边界条件(Liu and Sen，2010)压制因计算区域有限所引起的人工边界反射，对比分析震源归一化零延迟互相关成像条件与反褶积成像条件(Alejandro and Biondo，2002)，采用拉普拉斯滤波(Zhang and Sun，2009)压制逆时偏移成像产生的低频噪声.

目前，VSP逆时偏移主要以上行反射波作为有效波进行逆时延拓，但仅用上行反射波做逆时延拓会导致偏移成像结果照明度低、成像范围窄(Fleury，2013; Soni and Verschuur，2014)；并且当上行反射波作为有效波时，需要先进行波场分离，在波场分离中一般会对原始波场造成一定程度的损害，损失部分有效信息.本文以直达波除外的所有声波波场(全波)作为有效波，即一次多次波、多次反射波等都被视为逆时偏移的有效波进行逆时延拓.为验证全波VSP逆时偏移的有效性，本文采用上行波、下行波、全波分别作为逆时延拓的有效波，对层状模型、断层模型和Marmousi模型的VSP数据进行逆时偏移.模型试算的结果表明：以全波作为有效波的成像范围大、成像效果好.为验证自适应优化有限差分方法的效率与精度，本文将该方法与自适应泰勒级数展开有限差分方法和固定算子长度的泰勒级数展开有限差分法进行了对比分析.分析结果表明：与固定算子长度的泰勒级数展开有限差分法相比，自适应优化有限差分方法可以在不降低精度的前提下，较大地提高计算效率.最后，采用自适应优化有限差分方法、混合吸收边界条件、震源归一化零延迟互相关成像条件以及拉普拉斯滤波去噪方法实现了某地区实际VSP资料的逆时偏移，进一步验证了本文方法的有效性.

2 方法原理

2.1 优化有限差分方法

二维声波波动方程为

(1)

其中，p为标量波场，v为速度，t为时间，x、z为空间坐标.

VSP逆时偏移的震源正向延拓和地震记录逆时延拓的表达式分别为

(2)

(3)

其中，pF为震源延拓波场，pB为逆时延拓波场，f(t)为震源，δ为脉冲函数，Q(xr,zr;t)为地震记录，(xr,zr)为检波点坐标，(xs,zs)为炮点坐标.

分别采用二阶中心差分计算二阶时间导数和2M阶精度差分计算二阶空间导数，公式(2)和(3)变形为

(4)

(5)

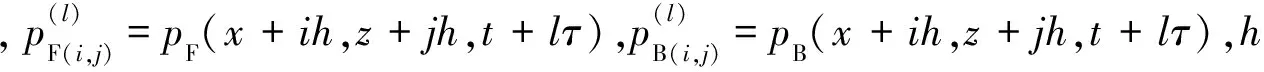
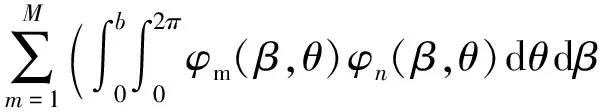
(6)

(7)

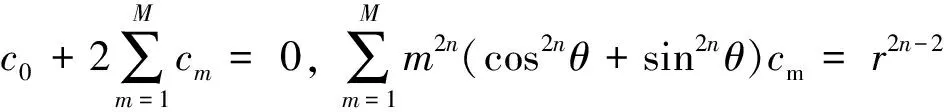
(n=1,2,…,M).

(8)

二维声波波动方程数值模拟的相速度频散δ表示为

(9)

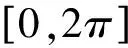
(10)

当δmax越趋向于1，频散越小.

图1是优化有限差分方法(optimal-basedFDmethod)、空间域泰勒级数展开有限差分方法(spaceTE-basedFDmethod)和时空域泰勒级数展开有限差分方法(time-spaceTE-basedFDmethod)的频散曲线对比图.由图可见：优化有限差分方法在区间[0，π]内，总体比空间域泰勒级数展开有限差分方法和时空域泰勒级数展开有限差分方法的数值频散都小，并且空间域泰勒级数展开有限差分方法和时空域泰勒级数展开有限差分方法的频散相近.

2.2 自适应变空间差分算子长度方案

在求解波动方程时，通常采用固定的算子长度计算空间导数，而自适应变空间差分算子长度方案采用变化的算子长度计算空间导数.自适应变差分算子长度方案是基于算法的精度控制不同速度网格点的M值，其表达式为(Liu and Sen，2011)

(11)

(12)

其中，ε为单位网格内传播时间的相对误差，fmax为子波最大频率，η为最大误差范围.利用公式(12)可以自动确定不同速度网格点的M值.一般在速度小的网格点用长空间差分算子，在速度大的网格点用短空间差分算子.这种方法可以在不降低模拟精度的情况下，提高计算效率.

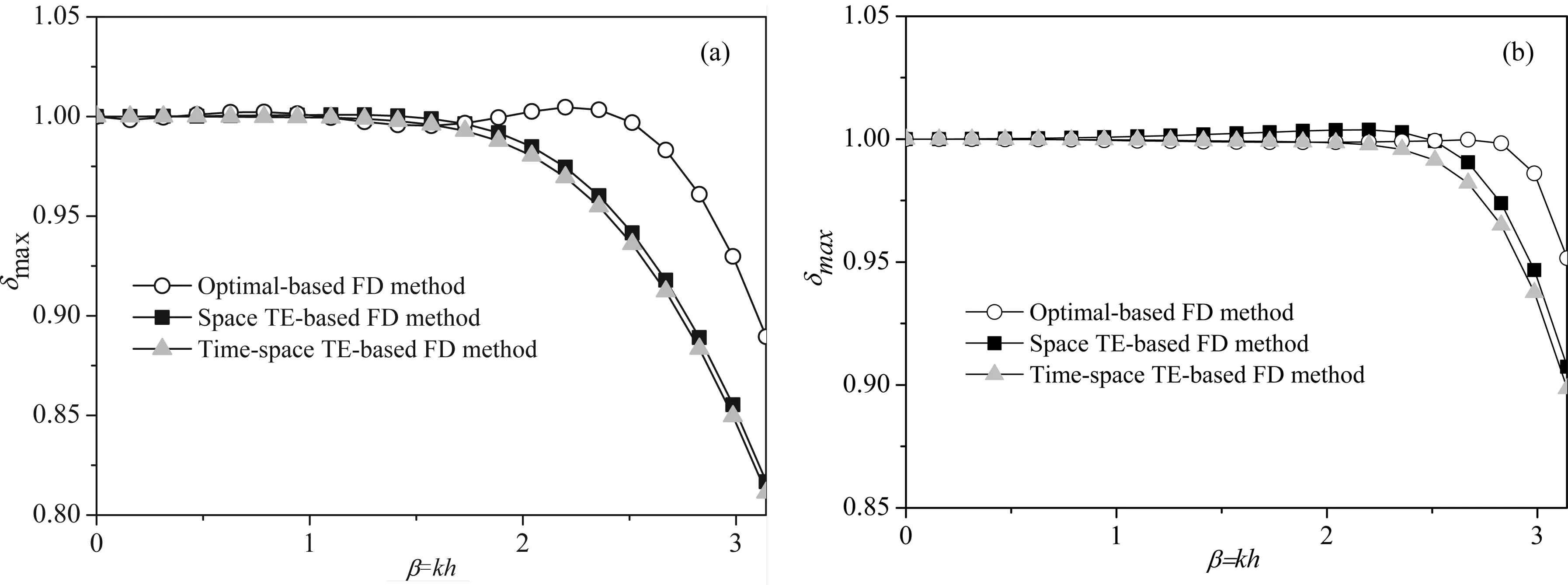
图1 优化有限差分、空间域泰勒级数展开有限差分和时空域泰勒级数展开有限差分方法的最大频散值δmax频散曲线(b=2.74，r=0.15)(a) M=4; (b) M=14.Fig.1 Maximum dispersion value δmax curves for the optimal-based FD method, the space TE-based FD method and time-space TE-based FD method (b=2.74， r=0.15)

为验证自适应变空间差分算子长度方案的有效性，设计一个速度模型，其速度的变化范围为1500～5000 m·s-1，h=10 m，τ=1 ms，fmax=40 Hz，同时对比自适应优化有限差分方法(adaptive optimal-based FD method)、自适应时空域泰勒级数展开有限差分方法(adaptive time-space TE-based FD method) (后文中的时空域泰勒级数展开有限差分方法(time-space TE-based FD method)简写为泰勒级数展开有限差分法(TE-based FD method))在相应的速度网格点的M值，最大误差η分别为10-4、10-5.图2为M随速度的变化图，由图可知：

(1) 对于相同的η，速度越小，M值越大；

(2) 对于优化有限差分方法，η越小，则精度越高，M越大；

(3) 当η=10-5时，优化有限差分方法的M比泰勒级数展开有限差分法的更小，即计算效率更高.

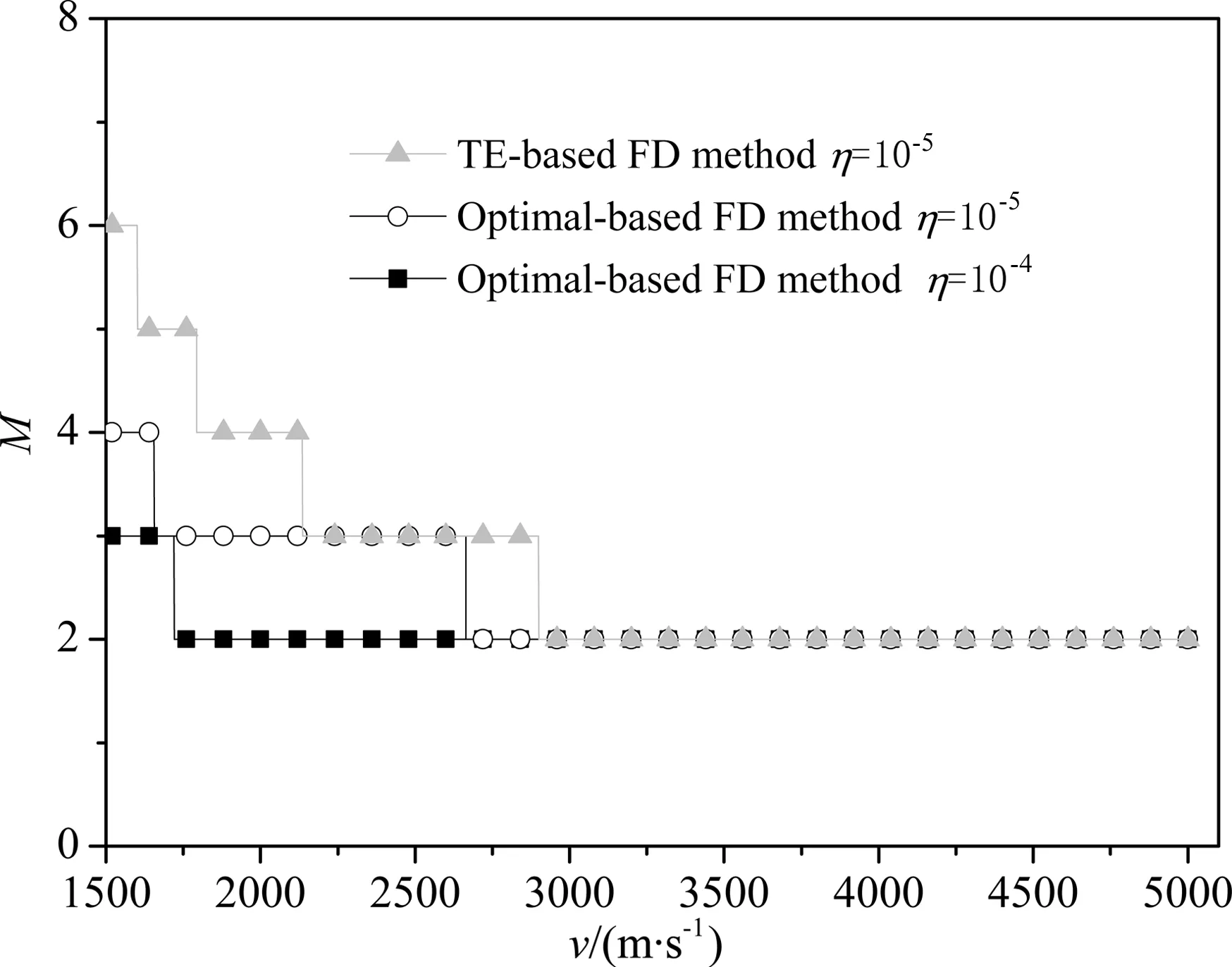
图2 有限差分算子长度参数M随速度变化图Fig.2 Variation of FD operator length parameter M with velocity

2.3 混合吸收边界条件

在VSP逆时偏移中，一个不可避免的问题是如何有效压制由计算区域边界引起的边界反射能量，本文采用混合吸收边界条件进行压制.混合吸收边界条件的基本原理是把计算区域分为内部区、过渡区、边界区.第一步，采用双程波波动方程计算内部区和过渡区波场值；第二步，采用单程波波动方程计算边界区与过渡区波场值；第三步，采用双程波波场值与单程波波场值的线性加权得到过渡区最终波场值.过渡区起到了对波场平滑过渡的作用，避免由内部区的双程波波动方程到边界区的单程波波动方程的急剧变化而导致的边界干扰反射无法得到有效压制的问题.以模型的上边界和左上角为例，其单程波波动方程表达式分别为(Clayton and Engquist，1997；Liu and Sen，2010)

(13a)

(13b)

当过渡区的网格厚度为1时，混合吸收边界条件等效于Clayton-Engquist吸收边界条件；过渡区网格厚度为10时能达到较好的吸收效果.以重新采样后的Marmousi速度模型(图3)为例，速度模型大小为5000m×3500m，震源是位于(2500m，0m)的主频为30Hz的Ricker子波，h=10 m，τ=1 ms，记录时间为4 s.图4为Marmousi速度模型的无边界条件与边界网格点数为10的混合吸收边界条件模拟地震记录，由图可见混合吸收边界条件能有效地压制边界反射.

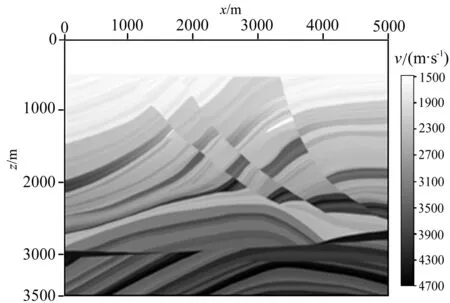
图3 Marmousi速度模型Fig.3 Marmousi velocity model

2.4 震源归一化零延迟互相关成像条件与反褶积成像条件的对比分析

震源归一化零延迟互相关成像条件的表达式为(Chattopadhyay and Mcmechan，2008)

(14)

其中，S(x,z,t)表示震源波场，R(x,z,t)表示检波点波场，Tmax为地震记录长度，I(x,z)表示反射系数，μ是稳定因子.

反褶积成像条件的表达式为(Alejandroetal., 2002)

(15)

(16)

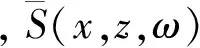
为对比震源归一化零延迟互相关成像条件与反褶积成像条件的成像效果，设计一个双层层状模型，模型大小为1000m×1000m，h=10 m，τ=1 ms，震源为主频为30 Hz的Ricker子波，混合吸收边界过渡区网格点数为10，自适应变空间算子长度方案参数为fmax=75 Hz、η=10-4，记录长度为1 s.观测系统参数为：地面放炮，炮点x坐标范围为0～990 m，炮间距为100 m，共10炮；5个检波点位于x=500 m，z=610～650 m处，检波点间距为10 m.图5为该层状模型的VSP逆时偏移成像结果.图5 a、d的对比表明：反褶积成像条件比互相关成像条件分辨率高.但是从图5b—d可以看出：稳定因子对反褶积成像的影响较大，如果μ取值不当会造成严重成像噪声.因此，本文采用震源归一化零延迟互相关成像条件实现VSP逆时偏移.

图4 Marmousi速度模型地震记录(a) 无边界条件; (b) 边界网格数为10的混合吸收边界条件.Fig.4 Seismic records for Marmousi velocity model(a) Non-ABC; (b) Hybrid ABC with the width of 10.

图5 VSP逆时偏移结果(a) 震源归一化零延迟互相关成像条件; (b) 反褶积成像条件，μ=0.01; (c) 反褶积成像条件，μ=0.6; (d) 反褶积成像条件，μ=1.Fig.5 Reverse VSP RTM results(a) Source-normalized cross-correlation imaging conditions; (b) Deconvolution imaging condition with μ=0.01; (c) Deconvolution imaging condition with μ=0.6; (d) Deconvolution imaging condition with μ=1.

图6 (a)倾斜界面模型; (b) 泰勒级数展开有限差分法，M=8; (c)泰勒级数展开有限差分法，M=32; (d)优化有限方法，M=8Fig.6 (a) Dipping reflector model; (b) TE-based FD method, M=8; (c) TE-based FD method, M=32; (d) Optimal-based FD method, M=8

3 模型算例

3.1 数值模拟

为了验证自适应优化有限差分方法的可行性，设计一个倾斜界面模型如图6 a所示，模型大小为4000 m×4000 m，h=20 m，τ=1 ms，数值模拟的震源采用主频为20 Hz的Ricker子波，且位于(2000 m，0 m)，混合吸收边界过渡区网格点数为10.分别采用泰勒级数展开有限差分法与优化有限差分方法实现波场模拟.图6b—d为1.2 s时刻数值模拟的波场快照，可见图6b的频散比较大，图6c与d频散相近，其结果表明：

(1) 对于相同算子长度(M=8)，优化有限差分方法(图6d)模拟精度高于泰勒级数展开有限差分方法 (图6b)；

(2)M=8时的优化有限差分方法(图6d)与M=32时的泰勒级数展开有限差分方法(图6c)模拟精度相近.

倾斜界面模型试算结果表明：在相同算子长度情况下，优化有限差分方法模拟精度高于泰勒级数展开有限差分方法模拟精度，表明了优化有限差分方法适用于求解波动方程空间差分系数，同时试算结果也表明混合吸收边界条件能有效地压制边界反射.

3.2 VSP逆时偏移

3.2.1 VSP全波逆时偏移分析

设计一个层状模型，其速度模型如图7所示，模型大小为1000 m×1200 m，h=10 m，τ=1 ms，记录时间为2 s，地表为自由边界，震源是主频为30 Hz 的Ricker子波.观测系统为：炮点位于(500 m，0 m)处，检波点位于(0 m，400 m)处.图8为检波点处地震记录，地震记录中可见直达波、一次反射波、一阶多次波、二阶多次波以及高阶多次波.分别对这5种波进行逆时偏移成像，偏移结果如图9所示，其中图9中深度z=650 m处的黑线为界面位置.图9表明：直达波只会造成炮点到检波点路径上的噪声(图9 a)；一次反射波在R1点处成像(图9 b)；一阶多次波在R2点处成像，与R1点相比，R2点距离井的位置更远(图9 c)，所以多次波可以拓宽成像区域；二阶多次波可以贡献两个成像点(图9 d)，一个比R1点距井源更近，一个比R2点距井源更加远，说明了多次波可以增加照明度及拓宽成像范围；高阶多次波的成像范围比R1点到R2点相距范围更广(图9e中箭头所示).以上5种波中，直达波和一阶多次波为下行波；一次反射波和二阶多次波为上行波；高阶多次波中既有上行也有下行波，如图8所示，其能量比一次反射波能量弱.若只用上行反射波作为逆时偏移的有效波场则会损失部分有效信息.理论分析表明：除直达波以外的所有波场对界面的成像均有贡献，所以多次波可以作为有效波进行逆时延拓，以增加照明度、拓宽偏移成像范围.

3.2.2 模型试算

首先，我们针对层状介质模型分别实现自适应优化有限差分方法和自适应泰勒级数展开有限差分方法的VSP逆时偏移，以验证自适应优化有限差分方法的有效性和效率.其次，我们采用自适应优化有限差分方法完成三个模型试算，分别用分离后的上行波、分离后的下行波以及分离前的全波实现VSP逆时偏移，下文中逆时偏移采用的波场均不包括直达波.虽然上行波包括一次反射波以及多次波，但是直达波除外的下行波都是多次波.我们采用下行波偏移即多次波偏移，偏移效果可以证明多次波偏移的有效性，而上行波偏移结果与全波偏移结果的对比也可以验证全波偏移的优越性.

(I) 层状模型

模型如图10 a所示，模型大小为4000 m×4000 m，h=20 m，τ=1 ms，震源为主频为20 Hz的Ricker子波，记录长度为2.5 s.混合吸收边界过渡区网格点数为10.自适应变空间算子长度方案参数为fmax=30 Hz，η=5×10-6.观测系统参数为：地面放炮，炮点x坐标范围为0～3980 m，炮间距为20 m，共200个炮点；检波点位于x=2000 m，z=0～1980 m，检波点间距为20 m，共100个检波点.图10b、c分别为

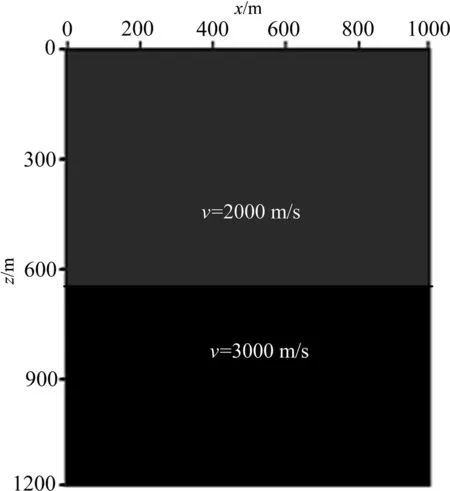
图7 层状介质速度模型Fig.7 Layered velocity model

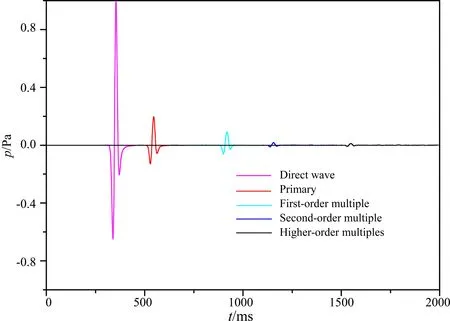
图8 层状介质模型的地震记录Fig.8 Seismic record for the layered model

图9 VSP逆时偏移分别采用 (a) 直达波; (b) 一次反射波; (c) 一阶多次波; (d) 二阶多次波; (e) 高阶多次波Fig.9 VSP RTM results with (a) Direct wave; (b) Primary wave; (c) First-order multiple; (d) Second-order multiple;(e) Higher-order multiples

自适应泰勒级数展开有限差分方法和自适应优化有限差分方法的VSP逆时偏移成像结果，从图10中可以看到自适应泰勒级数展开有限差分方法的VSP逆时偏移成像结果中有连续的虚假界面出现，其假轴由数值模拟中的频散产生；自适应优化有限差分VSP逆时偏移成像中构造清晰，无假轴出现.所以，在算子长度相同的前提下，自适应优化有限差分VSP逆时偏移成像精度更高，以下VSP逆时偏移均采用自适应优化有限差分方法.

我们设计另一个层状模型(图11)分析多次波在VSP逆时偏移中的影响.模型大小为2000 m×3000 m，h=10 m，τ=1 ms，记录总时长为2.5 s，震源是主频为30 Hz的Ricker子波，混合吸收边界过渡区网格数为10.自适应变空间算子方案参数为

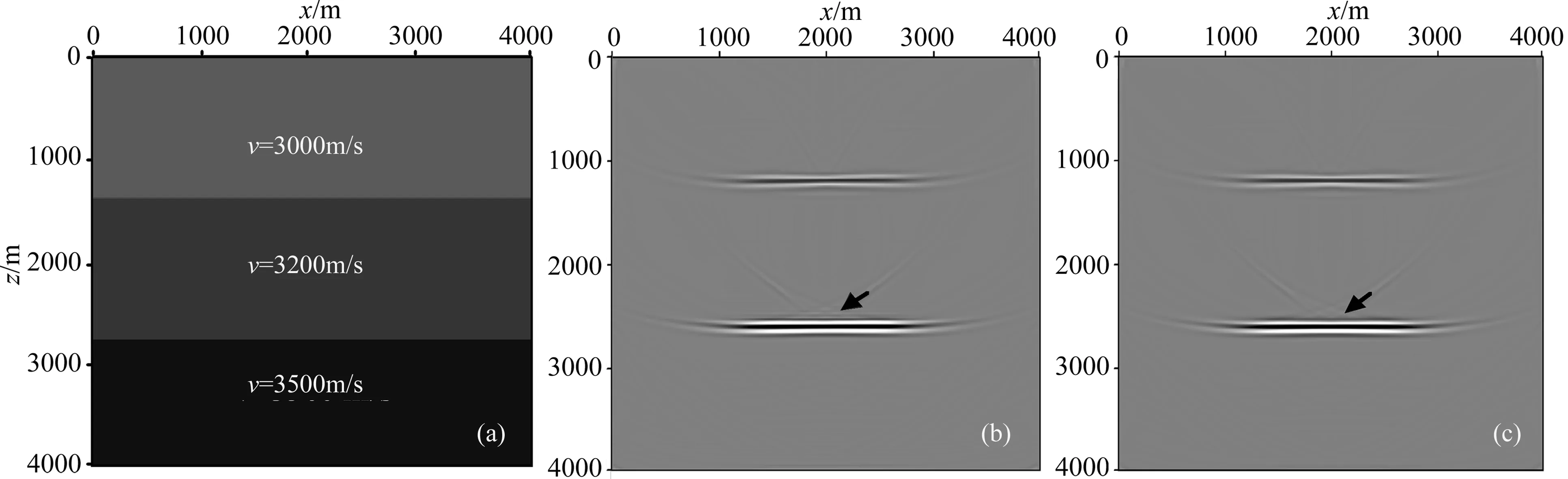
图10 (a) 层状速度模型; (b) 自适应泰勒级数展开有限差分法，M=2～3; (c) 自适应优化有限差分方法，M=2～3.Fig.10 (a) Layered velocity model; (b) Adaptive TE-based FD method FD method, M=2～3; (c) Adaptive optimal-based FD method, M=2～3.

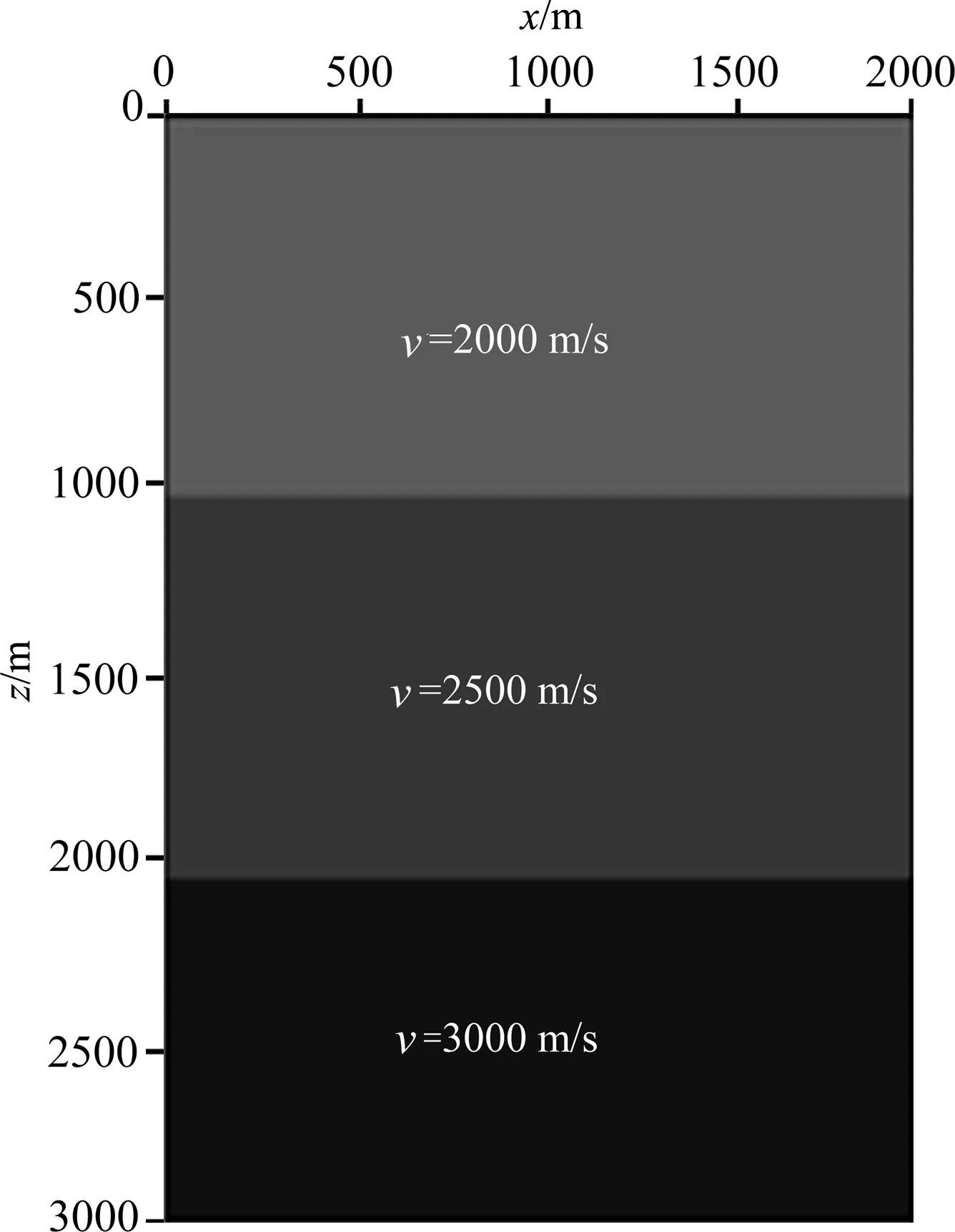
图11 层状模型Fig.11 Layered velocity model

fmax=40 Hz，η=10-5.观测系统为地面放炮，炮点x坐标范围为0～2000 m，炮间距为50 m，共41个炮点.检波点为x=1950 m,z=0～3000 m，检波点间距为10 m，共301个检波点.图12a—c分别为x=1950 m、z=0 m的炮点波场分离后上行波记录、下行波记录和切除直达波的全波记录.图13为逆时偏移成像结果，可得：

(1) 上行波作为有效波时(图13 a)，成像位置准确，井旁界面成像清晰；

(2) 下行波作为有效波时(图13 b)，远井源距的界面成像比上行波偏移成像结果更清晰，而井旁界面成像不如上行波偏移好，成像结果有一定噪声，但其噪声能量较弱；

(3) 全波作为有效波(图13c)时，井旁界面和远井源距界面均准确成像.由于下行波成像的噪声能量与上行波的成像能量差异大，在全波成像结果中几乎看不到成像噪声.

此层状模型试算结果表明，全波作为有效波时成像效果比仅用上行波或者仅用下行波作为有效波的成像效果更好.

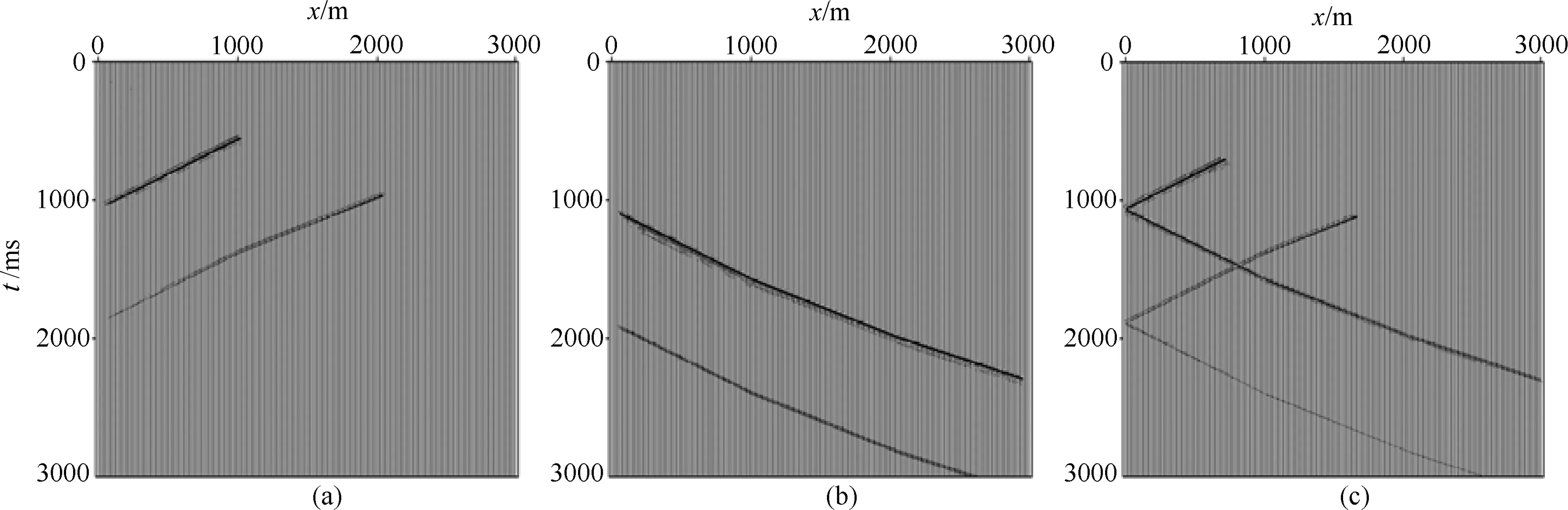
图12 层状模型的VSP地震记录(a) 上行波场; (b) 下行波场; (c) 全波波场.Fig.12 Seismic records for layered model(a) Up-going wavefield; (b) Down-going wavefield; (c) Full-wavefield.

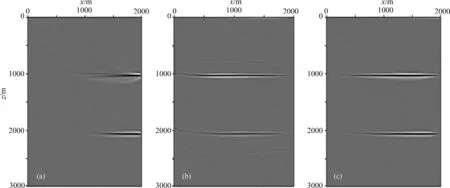
图13 VSP逆时偏移结果(a)上行波作为有效波; (b) 下行波作为有效波; (c) 全波波场作为有效波.Fig.13 VSP RTM results(a) Up-going wavefield as input; (b) Down-going wavefield as input; (c) Full-wavefield as input.

(II) 断层模型

断层速度模型(图14)大小为2000 m×2000 m，h=10 m，τ=1 ms，记录总时间为2 s，震源是主频为30 Hz的Ricker子波，混合吸收边界过渡区网格数为10，自适应变空间算子长度方案参数为fmax=50 Hz，η=10-5.观测系统参数为：地面放炮，炮点x坐标范围为0～2000 m，炮间距为100 m，共21个炮；检波点位于x=2000 m，检波点深度范围为0～2000 m，检波点间距为10 m，共201个检波点.图15为VSP逆时偏移成像结果，可见：

(1) 上行波、下行波、全波波场分别作为有效波时，VSP逆时偏移成像位置都准确；

(2) 上行波作为有效波时(图15a)，井旁界面成像较清晰；

(3) 下行波作为有效波时(图15b)，噪声比上行波偏移成像噪声严重；

图14 断层速度模型Fig.14 Fault velocity model

图15 断层模型VSP逆时偏移结果(a) 上行波作为有效波; (b) 下行波作为有效波; (c)全波波场作为有效波.Fig.15 VSP RTM result for fault model(a) Up-going wavefield as input; (b) Down-going wavefield as input; (c) Full-wavefield as input.

(4) 全波VSP逆时偏移成像结果(图15c)比仅用上行波或者下行波逆时偏移成像界面形态更清晰.

对于此断层模型，全波VSP逆时偏移成像的结果比仅用上行波或下行波成像结果更理想.

(III) Marmousi模型

层状模型与断层模型试算表明了全波在简单构造中VSP逆时偏移中的有效性，下面针对复杂构造模型进行试算.以Marmousi速度模型(图3)为例，τ=1 ms，记录长度为4 s，震源为主频为30 Hz的Ricker子波，混合吸收边界条件的过渡带点数为10，自适应变空间算子长度方案参数为fmax= 75 Hz，η=10-4，差分算子长度参数M为2～6.观测系统参数为：地面放炮，炮点x坐标范围为0～5000 m，炮间距为250 m，共21个炮点；检波点位于x=0 m，检波点深度范围为0～3500 m，检波点间距为10 m，共351个检波点.图16a—c分别为炮点位于(0 m，0 m)的上行波、下行波、全波的VSP地震记录.图17为Marmousi速度模型VSP逆时偏移成像结果，由图可知：

(1) 上行波、下行波及全波VSP逆时偏移成像位置准确，构造清晰；

(2) 上行波作为有效波时(图17a)，井旁构造成像较清晰，但远井源距处成像结果不清晰，部分构造无法显现；

(3) 下行波作为有效波时(图17b)，远井源距构造成像效果较好，但近井源距成像结果不如上行波成像结果连续；

(4) 全波作为有效波时(图17c)，井旁构造更为清晰、连续，并且远井源距构造也能较好成像.

波场分离后的上行波和下行波，都有部分波场信息的丢失，同时在波场分离中难免会损害部分有效信号，而全波波场信息较全，所以采用全波进行VSP逆时偏移效果更好.

为验证自适应优化有限差分算法的效率性，我们做了一个计算效率测试，CPU的型号是Intel(R) Xeon(R) CPU E5-26400 @ 2.5GHz，分别采用固定算子长度的泰勒级数展开有限差分方法(fixed-length TE-based FD method)、自适应泰勒级数展开有限差分方法(adaptive TE-based FD method)、自适应优化有限差分方法(adaptive optimal-based FD method)三种有限差分方法实现Marmousi模型全波VSP逆时偏移.以上三种有限差分方法的M值如图18所示.图19a—c分别为以上三种有限差分方法在时刻t=1200 ms时的波场快照.由图19可见，这三种有限差分方法的波场快照模拟精度相近，图19d为固定算子长度的泰勒级数展开有限差分方法M=7(图19a)与自适应优化有限差分方法M=2～4(图19c)波场快照的差值，由图19d可知，两者的误差很小，即两者的精度相近.本文对比了以上三种方法的效率(表1)，可得如下结论：

(1) 自适应泰勒级数展开有限差分方法与固定算子长度的泰勒级数展开有限差分方法对比，效率提高了15%左右；

(2) 自适应优化有限差分方法与固定算子长度的泰勒级数展开有限差分方法对比，计算量约节省了28%.

图16 Marmousi模型的VSP地震记录，炮点位于(0 m, 0 m)(a)上行波场; (b)下行波场; (c)全波波场.Fig.16 VSP seismic records for Marmousi model with source located at (0 m, 0 m)(a) Up-going wavefield; (b) Down-going wavefield; (c) Full-wavefield.

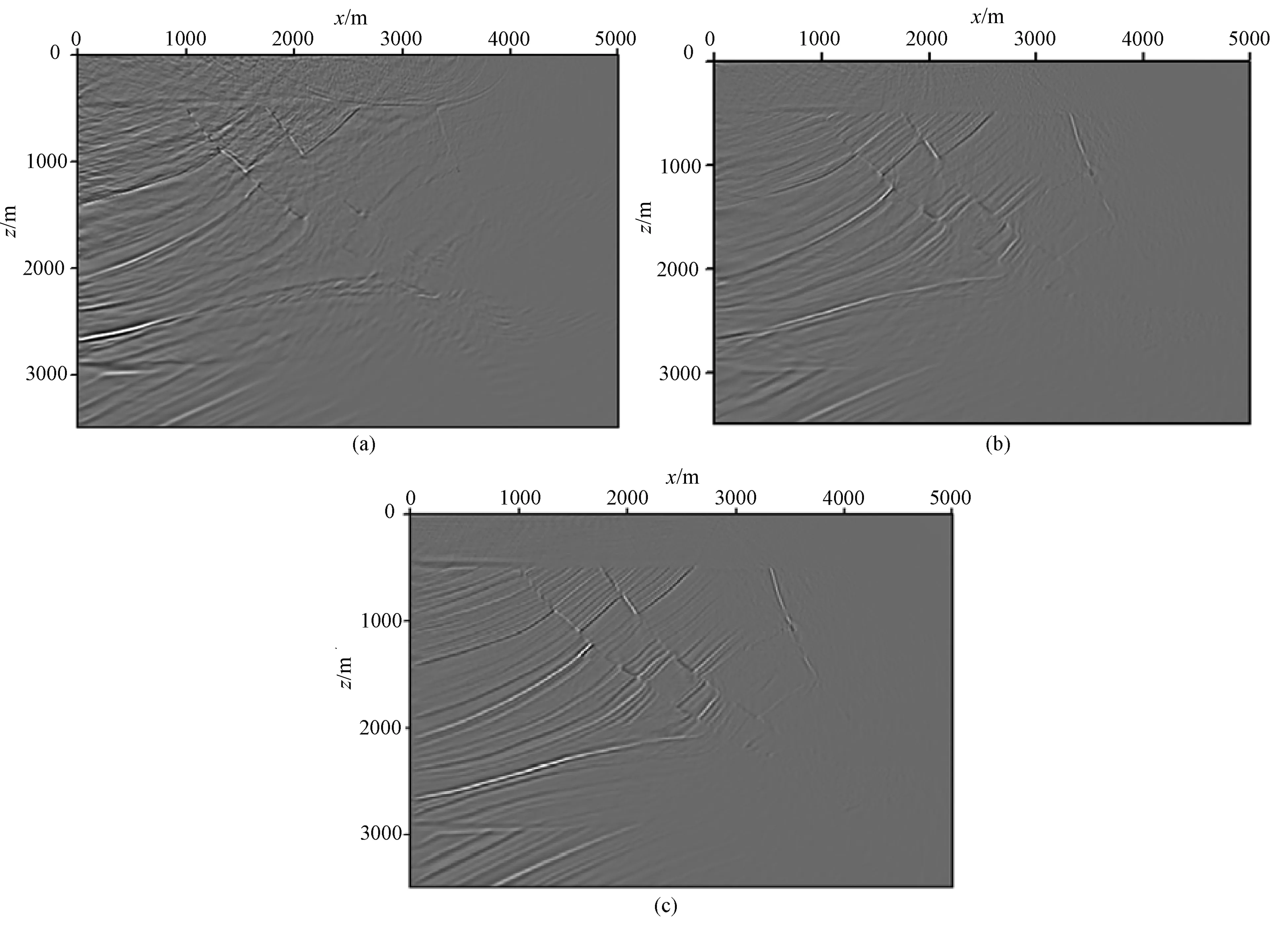
图17 VSP逆时偏移成像结果(a) 以上行波场为有效波; (b) 以下行波场为有效波; (c) 以全波波场为有效波.Fig.17 VSP RTM imaging result(a) Up-going wavefield as input; (b) Down-going wavefield as input; (c) Full-wavefield as input.

图19 Marmousi模型波场快照(a) 固定算子长度的泰勒级数展开有限差分法; (b) 自适应泰勒级数展开有限差分法; (c) 自适应优化有限差分方法; (d) 为(a)与(c)的误差图.Fig.19 Snapshots for Marmousi model(a) Fixed-length TE-based FD method FD method； (b) Adaptive TE-based FD method FD method； (c) Adaptive optimal-based FD method； (d) Error of (a) and (c).

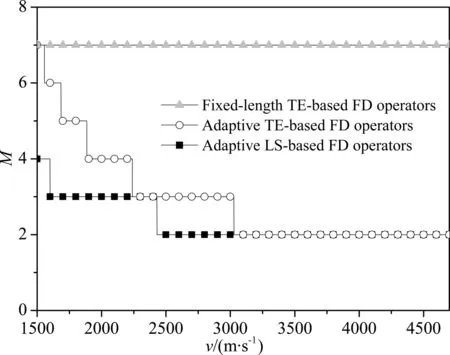
图18 优化有限差分方法与泰勒级数展开有限差分方法的算子长度参数M随速度变化图Fig.18 Variation of FD operator length parameter M with velocity by optimal-based FD method and TE-based FD method

图19表明了自适应优化有限差分方法的精度，图18和表1表明了该方法的效率性.综上所述，相同精度前提下，在固定算子长度的泰勒级数展开有限差分方法中引入自适应变空间差分算子长度方案可以提高计算效率；再用优化有限差分方法替代泰勒级数展开有限差分方法可以进一步提高计算效率.

表1 自适应优化有限差分方法逆时偏移效率Table 1 The efficiency of the adaptive optimal-based FD RTM

3.2.3 实际资料处理

为进一步验证自适应优化有限差分方法的VSP逆时偏移的有效性与正确性，本文将该有限差分方法应用于某地区的实际VSP资料逆时偏移中.原始地震记录为395炮，炮间距不固定，单个共检波点道集如图20a所示，其炮点没有位于整网格点上.本文采用抗泄露Fourier变换规则化重建方法(Gao et al., 2011)对图20a处理，规则化后共411炮，炮间距为10 m，如图20b所示.检波器深度为610～1000 m，共40道，道间距为10 m，每道记录长度为3.5 s，h=10 m，τ=1 ms.速度模型如图21所示.我们采用自适应优化有限差分方法、混合吸收边界条件、震源归一化零延迟互相关成像条件及拉普拉斯滤波去噪方法实现该VSP实际资料的逆时偏移，其中自适应变空间算子方案参数为fmax=75 Hz，η=10-4，其差分算子长度参数M=2～6，混合吸收边界过渡区网格点数为10.我们采用共检波点道集实现VSP逆时偏移.有效成像区域的偏移结果如图22 a所示，图22 b为实际资料的地面常规偏移的结果，图22 c为VSP逆时偏移剖面嵌入地面地震偏移剖面图.由图22可见，VSP逆时偏移成像同相轴清晰可辨，与地面地震成像结果构造的走向相同，VSP剖面与地面地震剖面部分层位的略有错位，这种错位主要是速度模型不准导致的，准确的速度模型的建立还有待进一步的研究.

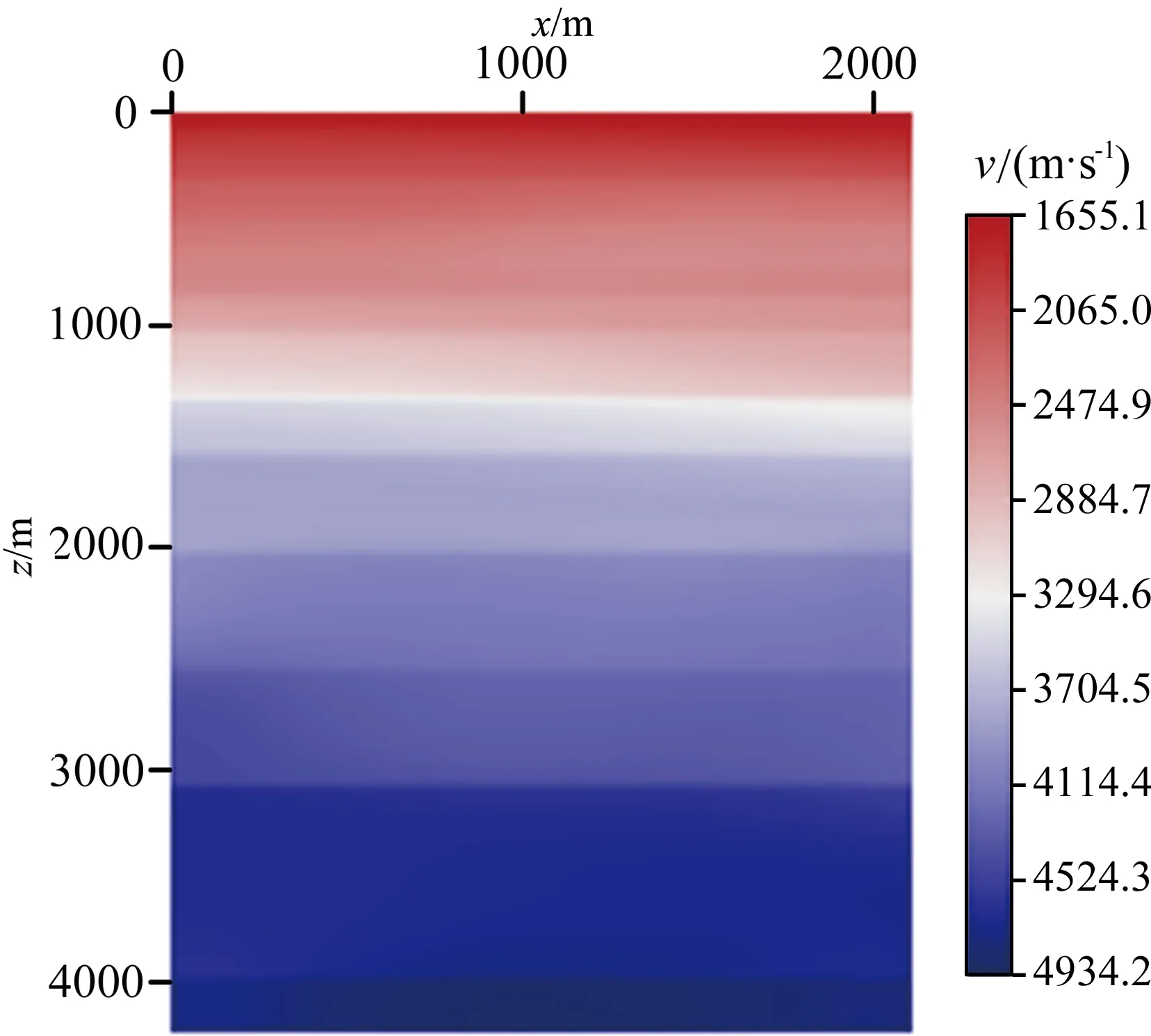
图21 实际资料速度模型Fig.21 Field data velocity model

4 讨论

相对于地面地震资料而言，VSP资料能更好地反映井旁信息，所以理论上对井旁的成像处理有着天然的优势.如果能结合VSP资料与地面资料进行井地联合逆时偏移，理论上可以更加清晰地描述地下构造.以图3所示的Marmousi速度模型为例，分别实现地面逆时偏移和VSP逆时偏移，地面勘探的观测系统为地面放炮，炮点x坐标范围为0～4900 m，炮间距为100 m，共50炮，地面接收，接收点x坐标范围为0～4990 m，检波点间距为10 m，共500个检波点.VSP资料的炮点观测系统与地面勘探相同，其检波点坐标位于x=0 m，井中接收点深度为0～3490 m，检波点间距为10 m，共有350个检波点.地面资料与VSP资料逆时偏移的参数均为：τ=1 ms，总记录时间为4 s，混合吸收边界过渡区网格点数为10，震源为主频为30 Hz的Ricker子波，自适应变空间算子长度方案参数为fmax=75 Hz，η=10-4，M=2～6.地面逆时偏移(图23 a)在深度为0～1000 m的水平构造和小倾角构造清晰，深度为2000～3000 m的角度不整合、地层隆起都得到了较好成像.VSP逆时偏移(图23 b)是以全波作为逆时延拓的有效波，VSP逆时偏移成像的井旁构造和中浅部大倾角构造(如箭头处)的成像效果比地面逆时偏移的效果好.图23c为两口井分别位于x=0 m和x=5000 m的VSP记录以及地面地震记录进行联合逆时偏移成像(井地联合逆时偏移)结果.图23a—c结果表明：井地联合成像结果(图23c)结合了VSP逆时偏移与地面逆时偏移的优点，其成像在井旁构造、大和小倾角构造、水平层状构造、角度不整合和地层隆起构造区域成像结果都较好.针对于同时进行地面地震勘探与VSP地震勘探的区域，可以采用井地联合偏移方法实现地下构造的成像以进一步提高成像精度.

图22 (a) VSP逆时偏移结果; (b) 地面常规偏移结果; (c) VSP成像结果与地面成像结果的嵌入图Fig.22 (a) VSP RTM result; (b) Surface conventional migration result; (c) VSP RTM result merged into surface migration result

图23 (a) 地面逆时偏移; (b) VSP逆时偏移; (c) 井地联合逆时偏移Fig.23 (a) Surface RTM result; (b) VSP RTM;(c) Surface combining with VSP RTM

5 结论

本文采用自适应优化有限差分方法求解声波波动方程，该方法与泰勒级数展开有限差分方法的对比表明：在算子长度相同前提下，优化有限差分方法模拟精度和VSP逆时偏移成像结果精度更高；在精度相同的条件下，优化有限差分方法数值模拟及VSP逆时偏移效率更高；引入自适应变差分算子长度方案可以进一步提高VSP逆时偏移计算效率.VSP逆时偏移中，全波逆时偏移比上行波逆时偏移成像结果波场信息更全、构造形态更连续、成像范围更广，因为多次波在增加照明度以及拓展成像范围起到了较大的作用.本文通过模型试算与实际资料VSP逆时偏移处理有效验证了自适应优化有限差分方法声波VSP逆时偏移的有效性.

致谢 感谢国家自然科学基金项目(41074100，41474110)、教育部新世纪优秀人才支持计划(NCET-10-0812)和壳牌地球物理优秀博士生奖学金的资助.

Alejandro A V, Biondo B. 2002. Deconvolution imaging condition for reverse-time migration, Stanford Exploration Project, 112: 83-96.

Baysal E, Kosloff D D, Sherwood J W C. 1983. Reverse time migration.Geophysics, 48(11): 1514-1524.

Campbell A, Gross J, Walker B, et al. 2002. Evaluation of a near-salt reservoir with an offset VSP (a case study in the Gulf of Mexico). 72nd SEG meeting, Salt Lake City, Utah, USA, Expanded Abstracts, 2353-2356.

Causse E, Ursin B. 2000. Viscoacoustic reverse time migration.JournalofSeismicExploration, 9(1): 165-184.

Chang W, McMechan G A. 1986. Reverse-time migration of offset vertical seismic profiling data using the excitation-time imaging condition.Geophysics, 51(1): 67-84.

Chang W, McMechan G A. 1987. Elastic reverse-time migration.Geophysics, 52(10): 1365-1375.

Chang W, McMechan G A. 1990. 3D acoustic prestack reverse-time migration.GeophysicalProspecting, 38(7): 737-756.Chang W, McMechan G A. 1993. 3D prestack migration in anisotropic media.Geophysics, 58(1): 79-90.Chang W, McMechan G A. 1994. 3D elastic prestack reverse-time depth migration.Geophysics, 59(4): 597-609.

Chattopadhyay S, Mcmechan G A. 2008. Imaging conditions for prestack reverse time migration.Geophysics, 73(3): S81-S89.

Chon Y, Souza J, Planchart. 2003. Offset VSP imaging with elastic reverse-time migration. 73rd SEG meeting, Dallas, Texas, USA, Expanded Abstracts, 1079-1053.

Clayton R W, Engquist B. 1977. Absorbing boundary conditions for acoustic and elastic wave equations.BulletinoftheSeismologicalSocietyofAmerica, 6: 1529-1540.Dablain M A. 1986. The application of high-order differencing to the scalar wave equation.Geophysics, 51(1): 54-66

Du Q, Zhu Y, Zhang M Q, et al. 2013. A study on the strategy of low wavenumber noise suppression for prestack reverse-time depth migration.ChineseJournalofGeophysics, 56(7): 2391-2401, doi:10.6038/cjg20130725.

Fleury C. 2013. Increasing illumination and sensitivity of reverse-time migration with internal multiples.GeophysicalProspecting, 2013, 61: 891-906.Gao J, Chen X, Wang F F, et al. 2011. Study on regularized reconstruction of uneven seismic traces.ProgressinGeophysics, 26(3): 983-991, doi:10.3969/j.issn.1004-2903.2011.03.025.Harwijanto J A, Wapenaar C P A, Berkhout A J. 1987. VSP migration by shot record inversion.FirstBreak, 5(7): 247-255.

Hokstad K, Mittet R, Landral M. 1988. Elastic reverse time migration of marine walkaway vertical seismic profiling data.Geophysics, 63(5): 1685-1695.

Hornby B, Yu J, Sharp J A, et al. 2006. VSP: Beyond time-to-depth.TheLeadingEdge, 25: 446-452.

Hou A, He Q. 1990. VSP reverse time migration.JournalofChangchunUniversityofEarthScience(in Chinese), 20(2): 227-233.

Hu H, Liu Y, Chang X, et al. 2013. Analysis and application of boundary treatment for the computation of reverse-time migration.ChineseJ.Geophys. (in Chinese), 56(6): 2033-2042, doi:10.6038/cjg20130624.Ketil H, Rune M, Martin L. 1998. Elastic reverse time migration of marine walkaway vertical seismic profiling data.Geophysics, 63(5): 1685-1695.

Li B, Liu H, Liu G F. 2010. Computational strategy of seismic pre-stack reverse time migration on CPU/GPU.ChineseJ.Geophys. (in Chinese), 53(12): 2938-2943, doi:10.3969/j.issn.0001-5733.2010.12.017..

Li Z, Guo Z, Tian K. 2014. Least-square reverse time migration in visco-acoustic medium.ChineseJ.Geophys. (in Chinese), 57(1): 214-228, doi:10.6038/cjg20140118.

Liu H W, Li B, Liu H, et al. 2010a. The algorithm of high order finite difference pre-stack reverse time migration and GPU implementation.ChineseJ.Geophys. (in Chinese), 53(7):1725-1733.

Liu H W, Liu H, Zou Z. 2010b. The problems of denoise and storage in seismic reverse time migration.ChineseJ.Geophys. (in Chinese), 53(9): 2171-2180, doi:10.3969/j.issn.0001-5733.2010.07.024.

Liu Y, Sen M K. 2009. A new time-space domain high-order finite-different method for the acoustic wave equation.JournalofComputationalPhysics, 228: 8779-8806.

Liu Y, Sen M K. 2010. A hybrid scheme for absorbing edge reflections in numerical modeling of wave propagation.Geophysics, 75(2):A1-A6.Liu Y, Sen M K. 2011. Finite-difference modeling with adaptive variable-length spatial operators.Geophysics, 76(4): T79-T89.

Liu Y. 2013. Globally optimal finite-difference schemes based on least squares.Geophysics, 78(4): T113-T132.

Loewenthal D, Mufti I R. 1983. Reverse time migration in the spatial frequency domain.Geophysics, 48(5): 627-635.

Nicoletis L, Mendes M, Compte P, et al. 1995. Quantitative ray-born elastic migration of VSP’s data. 57th Annual International Meeting, European Association of Geoscientists and Engineers, Expanded Abstracts.

Soni A K, Verschuur D J. 2014. Full-wavefield migration of vertical seismic profiling data: using all multiples to extend the illumination area.GeophysicalProspecting, 62(4): 740-759.

Sun R, McMechan G A. 2010. Nonlinear reverse-time inversion of elastic offset vertical seismic profile data.Geophysics, 53(10): 1295-1302.

Sun W B, Sun Z D. 2010. VSP reverse time migration based on the pseudo-spectral method and its applications.ChineseJ.Geophys. (in Chinese), 53(9): 2196-2203, doi:10.3969/j.issn.0001-5733.2010.09.020.

Sun W, Sun Z, Zhu X. 2011. Amplitude preserved VSP reverse time migration for angle-domain CIGs extraction.AppliedGeophysics, 8(2): 141-149.

Wang B L, Gao J H, Chen W S, et al. 2012. Efficient boundary storage for seismic reverse time migration.ChineseJ.Geophys. (in Chinese), 55(7): 2412-2421, doi:10.6038/j.issn.0001-5733.2012.07.025.Whitmore N D. 1983. Iterative depth migration by backward time propagation. 53rd Annual International Meeting, SEG, 827-830.

Wu W, Lines L R, Lu H. 1996. Analysis of higher-order, finite-difference schemes in 3-D reverse time migration.Geophysics, 61(3): 845-856.

Xiao X, Leaney W S. 2010. Local vertical seismic profiling (VSP) elastic reverse-time migration and migration resolution: Salt-flank imaging with transmitted P-to-S waves.Geophysics, 75(2): S35-S47.

Xiao X, Schuster G T. 2009. Local migration with extrapolated VSP Green′s functions.Geophysics, 74(1): SI15-SI26.

Xu S, Zhang Y, Tang B. 2011. 3D angle gathers from reverse time migration.Geophysics, 76(2): S77-S92.

Yan H, Liu Y. 2013a. Acoustic prestack reverse time migration using the adaptive high-order finite-difference method in time-space domain.ChineseJ.Geophys. (in Chinese), 56(3): 971-984.Yan H, Liu Y. 2013b. Visco-acoustic prestack reverse-time migration based on the time-space domain adaptive high-order finite-difference method.GeophysicalProspecting, 2013, 61: 941-954.

Yoon K, Marfurt K J, Houston U, et al. 2004. Challenges in reverse time migration. 74th Annual International Meeting, SEG, Expanded Abstracts, 1057-1060.Zhang Y, Sun J, Gray S H. 2007. Reverse-time migration: Amplitude and implementation issues. 77th Annual International Meeting, SEG, Expanded Abstracts, 2145-2149.

Zhang Y, Sun J. 2009. Practical issues in reverse time migration:

true amplitude gathers, noise removal and harmonic-source encoding.FirstBreak, 26(1): 29-35.

Zhao Y, Liu Y, Ren Z. 2014. Viscoacoustic prestack reverse time migration based on the optimal time-space domain high-order finite-difference method.AppliedGeophysics, 11(1): 50-62.

Zhu J M, Dong M Y, Li C C. 1989. VSP reverse-time migration using two-way nonreflection wave equation.OilGeophysicalProspecting, 24(3): 256-270.

附中文参考文献

杜启振，朱钇同，张明强等. 2013. 叠前逆时深度偏移低频噪声压制策略研究. 地球物理学报，56(7)：2391-2401, doi:10.6038/cjg20130725.

高建军，陈小宏，王芳芳等. 2011. 不规则地震道数据规则化重建方法研究．地球物理学进展，26(3)：983-991, doi:10.3969/j.issn.1004-2903.2011.03.025.

侯安宁，何樵登. 1990. VSP数据的逆时偏移. 长春地质学院学报，20(2)：227-233.

胡昊，刘伊克，常旭等. 2013. 逆时偏移计算中的边界处理分析及应用. 地球物理学报，56(6)：2033-2042, doi:10.6038/cjg20130624.

李博，刘红伟，刘国峰等. 2010. 地震叠前逆时偏移算法的CPU/GPU实施对策. 地球物理学报，53(12)：2938-2943, doi:10.3969/j.issn.0001-5733.2010.12.017.

李振春，郭振波，田坤. 2014. 黏声介质最小平方逆时偏移. 地球物理学报，57(1)：214-2288, doi:10.6038/cjg20140118.

刘红伟，李博，刘洪等. 2010. 地震叠前逆时偏移高阶有限差分算法及GPU实现. 地球物理学报，53(7)：1725-1733, doi:10.3969/j.issn.0001-5733.2010.07.024.

刘红伟，刘洪，邹振等. 2010. 地震叠前逆时偏移中的去噪与存储. 地球物理学报，53(9)：2171-2180, doi:10.3969/j.issn.0001-5733.2010.09.017.

孙文博，孙赞东. 2010. 基于伪谱法的VSP逆时偏移及其应用研究. 地球物理学报，53(9)：2196-2203, doi:10.3969/j.issn.0001-5733.2010.09.020.

王保利，高静怀，陈文超等. 2012. 地震叠前逆时偏移的有效边界存储策略. 地球物理学报，55(7)：2412-2421, doi:10.6038/j.issn.0001-5733.2012.07.025.

朱金明，董敏煜，李承楚．1989. VSP的双程无反射波动方程逆时偏移. 石油地球物理勘探，24(3)：256-270.

(本文编辑 刘少华)

Full-wavefield VSP reverse-time migration based on the adaptive optimal finite-difference scheme

CAI Xiao-Hui1,2, LIU Yang1,2*, WANG Jian-Min3, WANG Wei-Hong3, REN Zhi-Ming1,2

1StateKeyLaboratoryofPetroleumResourcesandProspecting,ChinaUniversityofPetroleum,Beijing102249,China2CNPCKeyLaboratoryofGeophysicalProspecting,ChinaUniversityofPetroleum,Beijing102249,China3ExplorationandDevelopmentResearchInstituteofDaqingOilfieldCompanyLimited,Daqing163318,China

Vertical seismic profiling (VSP) data provides higher resolution information, lower environmental noise and better information beside wells than surface seismic data. Meanwhile, reverse-time migration (RTM) based on two-way wave equation has no dip limitations on the image. It is significant to implement the RTM on VSP data.The four key factors of RTM are wavefield extrapolation, absorbing boundary conditions (ABC), imaging condition and noise suppressing. For the first factor, the paper compares the finite-difference (FD) method based on optimal scheme (optimal-based FD method) with the FD method based on space Taylor series expansion (space TE-based FD method) and the FD method based on time-space Taylor series expansion (time-space TE-based FD method) to indicate the accuracy of the optimal-based FD method. Moreover, to improve the efficiency, the adaptive variable-length spatial operators method is introduced into the optimal-based FD method (adaptive optimal-based FD method). The adaptive optimal-based FD method is adopted to solve the acoustic wave equation and thus implements the wavefield extrapolation of RTM efficiently and accurately. Second, the hybrid ABC is used to suppress artificial reflections from the model boundaries caused by the limited computational boundaries. Then the paper compares normalized cross-correlation imaging condition with deconvolution imaging condition for imaging, which indicates the prior is more stable and efficient. Finally, the Laplace operator filtering is applied to remove the low frequency noises.The conventional migration from VSP data using only up-going primary wavefield often suffers from poor illumination and limited migration scope. To enhance the illumination, enlarge the migration scope and improve the accuracy, the analysis of VSP RTM imaging with direct wave, primary wave, first-order multiple, second-order multiple and higher-order multiples implies that the full-wavefield (complete acoustic wavefield data without direct wave) can be treated as effective wave to implement prestack RTM.RTM test on VSP model data shows that the adaptive optimal-based FD method is more efficient and accurate than the fixed-length TE-based FD method, and suitable to VSP RTM. VSP RTM result using full-wavefield is clearer and images a larger area than VSP RTM only using up-going field. Imaging test on VSP field data demonstrates the efficiency and accuracy of our method.

VSP; Adaptive optimal-based FD method; Full acoustic wavefield; RTM

蔡晓慧， 刘洋， 王建民等. 2015. 基于自适应优化有限差分方法的全波VSP逆时偏移.地球物理学报，58(9):3317-3334,

10.6038/cjg20150925.

Cai X H, Liu Y, Wang J M, et al. 2015. Full-wavefield VSP reverse-time migration based on the adaptive optimal finite-difference scheme.ChineseJ.Geophys. (in Chinese),58(9):3317-3334,doi:10.6038/cjg20150925.

10.6038/cjg20150925

P631

2014-08-14，2015-04-16收修定稿

国家自然科学基金项目(41074100，41474110)和教育部新世纪优秀人才支持计划(NCET-10-0812)联合资助.

蔡晓慧，女，1990年生，中国石油大学(北京)博士研究生，主要从事VSP地震资料处理和逆时偏移成像方面的研究工作. E-mail:caixh_1990@sina.com

*通讯作者 刘洋，男，1972年生，博士，教授，主要从事地震波正演、成像、反演及多分量地震等方面的研究工作.E-mail：wliuyang@vip.sina.com