基于磁耦合谐振的无线电能传输系统设计

侯正文，肖岚

(南京航空航天大学 自动化学院，江苏 南京 210016)

基于磁耦合谐振的无线电能传输系统设计

侯正文，肖岚

(南京航空航天大学 自动化学院，江苏 南京 210016)

基于磁耦合谐振的无线电能传输技术在众多传输技术中具有传输距离适中和效率较好的优点。阐述了磁耦合谐振式无线电能传输原理并建立等效互感理论模型进行参数分析，进一步基于不对称半桥和LC串联谐振电路拓扑分析了开关管占空比变化对输出功率的影响。设计了一种小功率无线电能传输系统，并通过仿真和实验，验证了理论分析和系统设计的正确性。

磁耦合谐振;无线电能;互感模型;占空比;不对称半桥

0 引言

19世纪末，物理学家尼古拉·特斯拉提出了无线电能传输的概念，并在美国纽约长岛上的沃登克里弗塔进行了无线电能传输实验，点亮了40.225 km外的氖气照明灯，开启了无线电能传输研究的热潮［1］。无线电能传输脱离了传统的实物导电介质，实现了“隔空”传递电能，因而具有众多异于有线电能传输方法的优点，包括电池充电的便捷性，水底等严苛场合下用电的安全性，也解决了像体内医疗仪器的用电等一些传统场合下无法使用有线传递电能的问题等［2－3］。目前无线电能传输技术共分为三类:电磁感应式、电磁辐射式和磁耦合谐振式。其中，磁耦合谐振式利用发射端和接收端具有相同的谐振网络和谐振频率产生磁场的强耦合作用实现电能的无线传输。该方法传输距离适中，效率相较于电磁辐射式较高，应用前景较为广泛。2007年6月美国麻省理工学院的研究团队利用该原理成功点亮了2 m外功率为60W 的灯泡［4］。

已有文献主要分析了电感、电容和电阻等电气器件参数对于传输功率的影响，少有针对电路本身参数对传输功率的影响的研究。本文从不对称半桥加串联谐振电路拓扑出发，分析了开关管占空比变化对传输功率的影响，并详细设计了基于磁耦合谐振的不对称半桥无线电能传输系统的结构和参数。最后，通过仿真和实验，验证了理论分析和系统设计的正确性。

1 磁耦合谐振式无线电能传输原理及分析

1.1 磁耦合谐振工作原理及互感模型

磁耦合谐振技术通过合理设计发生源，将电磁场的近区场作为无线电能高效传输的 介 质［5］。基于磁耦合谐振的无线电能传输技术的装置原理图如图1所示，其中LS和CS为输入侧发射回路的谐振电感和谐振电容，LD和CD为输出侧接收回路的谐振电感和谐振电容。当直流电源经高频逆变产生的交流电频率与发射线圈和谐振电容谐振频率一致时，产生最大的交变磁场。同时，当输入侧串联电感和电容的谐振频率和输出侧串联电感和电容的谐振频率相同时，耦合到输出侧的磁场强度最强，传输到接收线圈LD上的电能也最大，经后级整流滤波电路后，输出直流电能。整个传输过程中，发射线圈和接收线圈无直接接触，仅通过强磁场耦合进行电能传输。

图1 磁耦合谐振无线电能传输装置原理图

图2 磁耦合谐振式无线电能传输模型

考虑发射回路和接收回路的线路阻抗，建立如图2所示的等效电路模型，发射回路和接收回路采用串联谐振方式。US为输入直流电经高频逆变电路产生的高频交流电，ZS为电源内阻和发射回路导线的等效阻抗，ZD为接收回路导线的等效阻抗，LS和LD为发射回路和接收回路的谐振电感，CS和CD为发射回路和接收回路的谐振电容，ZL为负载阻抗，M为发射线圈和接收线圈间的互感系数，d为线圈之间的传输距离，M的大小主要取决于d的大小。

设高频交流电的角频率为ω，根据回路KVL定理及磁耦合谐振理论，解得发射回路和接收回路电流表达式如下:

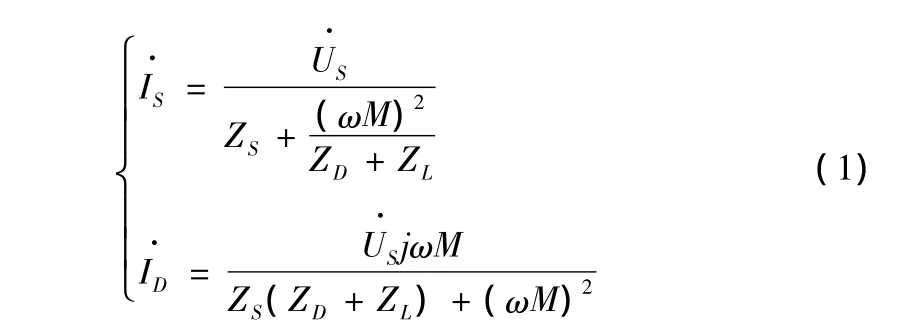
假设ZS、ZD和ZL均为纯阻性，则接收回路电感电流ID超前发射回路电感电流IS1/4个周期，输出功率Po表达式为［6］:

分析(2)式可知，当ω确定，M值随着d值确定后，输出功率Po随输入交流源电压有效值US的增大而增大，随发射回路阻抗ZS和接收回路阻抗ZD的增大而减小。因此，当系统处于磁耦合谐振状态时，提高系统输出功率，一方面增加输入交流电压的有效值来提高输入功率，另一方面降低回路阻抗来降低线路损耗。

1.2 占空比为D的矩形波输入电压

在等效互感理论模型中，输入交流电为标准的正弦，分析电路时采用的是传统的正弦电路分析法则。实际电路中LC谐振电路的输入波形往往是前级逆变电路产生的矩形波。本文基于不对称半桥和LC串联谐振电路拓扑设计小功率无线电能传输系统。该系统中，串联谐振电路的输入电压是占空比为D(D为半桥拓扑上桥臂开关管占空比)的矩形波，通过傅里叶分解可求得各次电压分量，根据电路叠加原理分别作用在谐振电路上。设矩形波电压幅值为Uin，周期时间为T，占空比为D。

根据周期性波形的傅里叶级数公式，可得:

式中Ui为输入电压，Udc为输入电压的直流分量，an、bn为n次正弦波形和余弦波形的幅值。

根据系数公式，结合矩形波特征量，可求得输入波形直流分量如下:

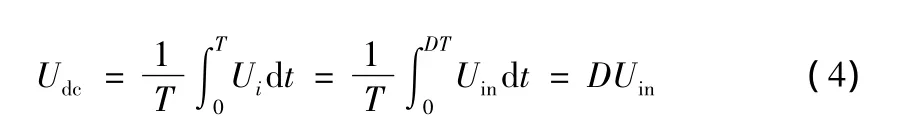
该直流分量与占空比D成正比。因为直流稳态下，电容相当于开路，电感相当于短路，谐振电容两端完全承受输入电压的直流分量。

同时可求得n次正弦谐波幅值系数和n次余弦谐波幅值系数，并得到n次谐波的总幅值系数An为:

根据(5)式可知，随着n值的增大，谐波的总幅值系数逐渐减小，因而，本文只考虑n=1时的基次谐波分量对LC谐振电路的影响。则有:

分析(6)式可知，当D=0.5时，A1取得最大值2Uin/π。因为余弦函数cos t关于t=π对称，因此，基次谐波分量幅值A1数值关于 D=0.5左右对称，在 D∈(0，0.5)区间，A1单调递增，在 D∈(0.5，1)区间，A1单调递减。

由此可知，可通过占空比D的调节改变输入正弦电压有效值，从而依据(2)式实现输出功率的调节。同时，应使占空比D位于(0，0.5)区间内，一方面符合控制系统的负反馈原理使系统的稳定性增加，另一方面结合(4)式可知，较小的D值可以降低谐振电容的电压定额，降低电路成本。

2 小功率无线电能传输系统设计

本文设计的小功率无线电能传输系统包括无线电能传输和传输系统控制两个部分。电路结构图如图3所示。为了稳定输出电压，在接收电路和 PWM电路之间加入负反馈，通过控制占空比D实现稳压作用。

图3 无线电能传输

图4 无线电能传输电路

2.1 无线电能传输电路设计

无线电能传输电路原理图如图4所示。发射电路部分，功率管Q1、Q2组成不对称半桥高频逆变电路，后接C1和L1串联谐振回路。Cin为输入电压源的滤波电容。接收电路部分，L2和C2构成串联谐振回路，D5～D8构成整流桥，电解电容C3滤波。设计C1=C2，L1=L2，使 L2、C2的谐振频率与 L1、C1的谐振频率相同，从而实现能量输出功率最大［7］。为了抑制高频产生的集肤效应，降低回路损耗，提高输出功率，采用内阻较小的利兹线绕制耦合电感。

2.2 传输系统控制电路设计

传输系统控制电路原理图如图5所示。

图5 传输系统控制电路

PWM电路部分，SG3525的11脚和14脚通过两个二极管形成或门电路，增大了输出PWM波的占空比范围;5脚、6脚和7脚构成三角波发生电路，利用6脚的可调电阻Raj1调节三角波频率从而控制PWM频率，使得与谐振频率一致实现最大电能传输;1脚、2脚和9脚构成反馈补偿电路，利用1脚的可调电阻Raj2对16脚的5.1 V基准电压进行分压作为补偿器的基准电压同时采样输出电压进行比较补偿，以实现改变占空比，稳定输出电压的作用，在开环状态下，通过在9脚输入控制电压与三角波电压交截可产生可控的占空比，实现对输出电压的可控调节。

驱动放大电路部分，主芯片采用ON Semiconductor公司生产的NCP5111。该芯片2脚输入为前级PWM电路输出的PWM波形，通过功率放大后4脚和3脚、6脚和7脚输出两路死区时间固定且互补的PWM波形驱动半桥开关管，有效避免了桥臂直通现象。芯片5脚和7脚间通过添加自举电容C10来存储足够电荷有效驱动不对称半桥电路的上桥臂开关管Q1。

3 仿真与实验结果

搭建基于上述设计方案的仿真和实验平台。无线电能传输距离为5 cm，输入电压Uin为20 V，开关频率(谐振频率)fs为250 kHz，串联谐振电容 C1、C2为 47 nF，串联谐振电感 L1、L2为 9 μH，RL为10Ω。

利用Saber软件对电路进行仿真。图6给出了发射线圈电感电流iS和接收线圈电感电流iD的波形。由图6可知，发射线圈和接收线圈的电感电流均为较好的正弦波形，同时接收线圈电感电流超前发射线圈电感电流1/4个周期，满足上述理论分析的结果。

图6 发射线圈和接收线圈电感电流仿真波形

图7给出了上桥臂开关管不同占空比D下上桥臂开关管驱动电压UGS1，发射回路谐振电容两端电压UC1以及输出电压Uout的波形。

对比图7各图可知，在占空比D=0.5时，输出电压大于D=0.4和 D=0.6时的输出电压，达到最大值，且D=0.4和 D=0.6时输出电压基本相同，满足理论分析结果。发射回路谐振电容电压的直流分量基本满足(4)式的理论推导。

图8给出了不对称半桥拓扑上下开关管Q1、Q2的驱动波形。由图8可知，上下开关管实现了互补导通，此处占空比D小于0.5。

图9给出了不对称半桥桥臂中点电压UDS2和发射线圈电感两端电压UL1波形。由波形可看出发射线圈电感两端电压波形为正弦波，桥臂中点电压波形为矩形波，矩形波的占空比D取决于上桥臂开关管占空比，此处D大于0.5。

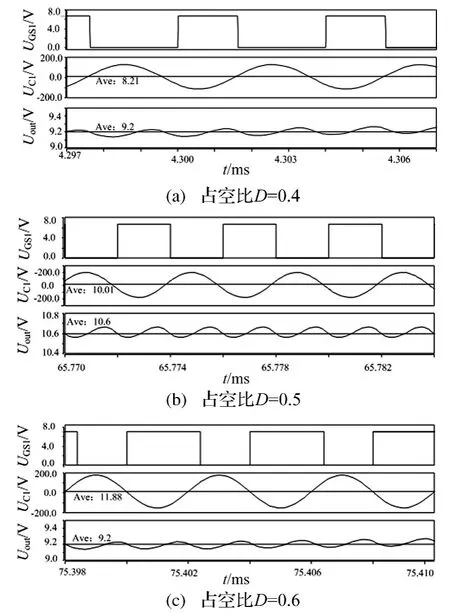
图7 不同占空比D下相关仿真波形

图8 不对称半桥上下开关管驱动波形

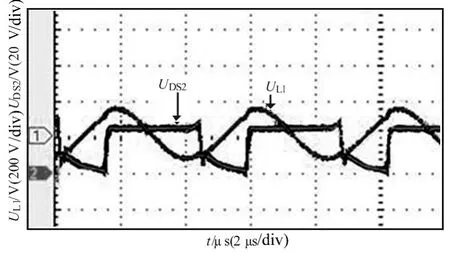
图9 桥臂中点电压和发射线圈两端电压波形

图10给出了下开关管Q2驱动占空比为0.64，即上开关管占空比D=0.36时的驱动波形UGS2和对应输出电压波形Uout。图中，输出电压约为10.05 V，输出功率为10.10 W，比仿真结果稍大，这是由于实验中传输距离5 cm所对应的互感系数M值比设置的仿真参数稍大引起的。

为了进一步验证不同占空比下输出电压的变化规律，对电路进行重复试验，记录不同占空比下对应的输出电压得到图11。

根据图11所示，输出电压近似关于D=0.5对称，这是因为其他次谐波的存在对输出电压产生微小影响。同时输出电压在D=0.5达到最大值，输出电压随着D的增大先增大后减小。实验结果符合理论分析。

图10 下开关管Q2驱动和输出电压波形

图11 输出电压—上开关管占空比D关系曲线

4 结束语

本文基于不对称半桥电路拓扑，利用傅里叶变换对LC串联谐振非正弦输入电压源进行了理论分析，得出了输入矩形波电压的占空比变化对输出功率的影响规律，据此设计并制作了一种小功率无线电能传输系统，通过仿真和实验进一步验证了占空比变化对输出功率带来的影响，符合理论研究的结果。

［1］杨庆新，陈海燕，徐桂芝，等.无接触电能传输技术的研究进展［J］.电工技术学报，2010，25(7):6 －13.

［2］马官营，颜国正.基于电磁感应的消化道内微系统无线能量传输问题研究［J］.生物医学工程学杂志，2008，25(1):61 －64.

［3］董文辉.一种新颖的双管超高频感应加热电路拓扑的研究［D］.浙江:浙江大学，2006.

［4］ ANDRE KURS，ARISTERDIS KARALIS.Wireless power transfer via strongly coupled magnetic resonances［J］.Science，2007，317(5834):83－86.

［5］赵争鸣，张艺明，陈凯楠，等.磁耦合谐振式无线电能传输技术新进展［J］.中国电机工程学报，2013，33(3):1 －13.

［6］陆洪伟.一种谐振式强磁耦合型无线充电系统的研究［D］.上海:上海交通大学，2012.

［7］柏杨，黄学良，邹玉炜，等.基于超声波的无线电能传输的研究［J］.压电与声光，2011，33(2):324－327.

Design of a W ireless Power Transm ission System Based on Magnetic Coupling Resonance

HOU Zheng-wen，XIAO Lan
(College of Automation，Nanjing University of Aeronautics and Astronautics，Nanjing Jiangsu210016，China)

Amongmany transmission technologies，the wireless power transmission technology based on magnetic coupling resonances has the advantages ofmoderate transmission distance and good efficiency.This paper elaborates the principle of wireless power transmission based on magnetic coupling resonances and establishes an equivalentmutual inductance theoretical model which helps to analyze parameters.Furthermore，based on asymmetric half bridge and LC serial resonance circuit，it analyzes the influence of the changes in duty ratios of the switching tube.A low-power wireless power transmission system is designed.The simulation and experimental results of the system are given to verify the correctness of theoretical analysis and system design.

magnetic coupling resonances;wireless power;mutual inductancemodel;duty;asymmetric half bridge

10.3969/j.issn.1000 －3886.2015.06.017

TM464

A

1000－3886(2015)06－0053－03

定稿日期:2015－01－08

侯正文(1991－)男，江苏南京人，硕士生，研究方向为功率电子变换器。 肖岚(1971－)女，江苏南京人，教授，研究方向为航空电源系统，逆变器并联、新能源发电系统。