模块化多电平变流器的混合调制策略

何大清

(上海电气集团股份有限公司 中央研究院，上海 200070)

模块化多电平变流器的混合调制策略

何大清

(上海电气集团股份有限公司 中央研究院，上海 200070)

简述模块化多电平变流器的应用和阶梯波调制的优点;分析采用基于拉格朗日乘子的阶梯波调制算法的原理，指出算法对多电平计算的优势，叙述利用牛顿－拉尔逊法实现该阶梯波计算的过程;计算阶梯波算法的调制范围，利用傅立叶分析对输出电压的谐波含量进行分析，确定调制比的合理范围;针对调制范围较窄的缺陷，提出用不同电平的阶梯波和多重载波混合调制的控制策略;通过对7电平的变流器的无功功率变化和低电压穿越进行仿真，对混合调制策略进行了验证;最后得出结论混合调制在提高模块化多电平变流器控制能力方面有显著效果。

模块化多电平变流器;阶梯波混合调制;拉格朗日乘子;傅立叶分析;低电压穿越

0 引言

模块化多电平变流器(multilevelmodular converter，MMC)是一种基于半桥串联的变流器结构［1］，目前在应用领域受到广泛关注。MMC的调制方可以是阶梯波法调制、多重载波调制、相移PWM 调制等［2］，鉴于 MMC 的主要优势是高电压、大功率［3］，采用阶梯波调制对减低滤波损耗和电磁干扰有显著作用［4］。阶梯波调制的关键是对由各电平触发角和各次波形组成的非线性方程组的计算，求解方程组的方法包括有:牛顿－拉尔逊法［5］，基于沃尔什函数的分段线性求解［6］，以及神经网络和遗传算法［7］等等，MMC的结构和输出阶梯波如图1所示。在阶梯电平较少时，这些算法取得不错的效果，但阶梯电平超过5个时，算法的复杂程度将大大增加，加剧处理器的计算负担和计算误差［8］。另外有用阶梯电平对参考波进行拟合的方法，只有电平数非常多时才能保证谐波含量，限制了MMC的应用范围。因此文献［9］提出了一种基于拉格朗日乘数的调制方法，将方程组的求解简化为对单一系数的求解，无论阶梯电平有多少，只要求解一个变量就可以，应用范围和计算速度大大加强。阶梯波也存在调制范围小的缺点，以级联型STATCOM(Static Synchronous Compensator)为例，只能应对10%的电网不对称［10］，而MMC用于可再生能源并网时，必须要保证低电压穿越功能，此时的调制比接近于零，要实现这个功能，单纯阶梯波调制是不可能的，因此要考虑如何对调制范围进行扩展。

本文针对MMC在可再生能源并网方面的应用，研究阶梯波和多重PWM混合调制策略。

1 拉格朗日乘子算法

由阶梯触发角和各次输出波形组成的方程组可表示为:

式中θi(i=1，2，…，n)是每个电平的触发角;n是电平数;M是基波调制比。Vsub表示电平幅值;Vh(h=1，3，…，2n－1)表示奇次波电压。因为输出为对称波形，不需要考虑偶次谐波。

阶梯波谐波含量用函数 f(θ1，θ2，…，θn)表式:

图1 MMC的结构和输出波形

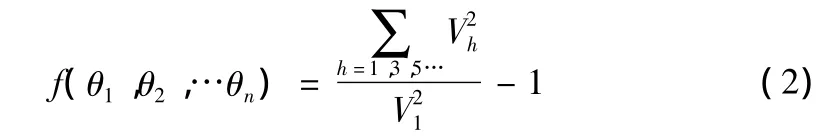
根据式(1)建立 f(θ1，θ2，…，θn)的约束条件:

由式(2)、(3)可得拉格朗日函数［9］:

设输出电压Vo，Vo在θk的瞬态值可表示为:

根据阶梯波形的特点，Vo(θk)又可表示为:

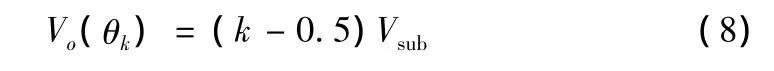
由于式(7)和式(8)等价，可以将式(6)转换为:

另外式(5)的右边可表示为:

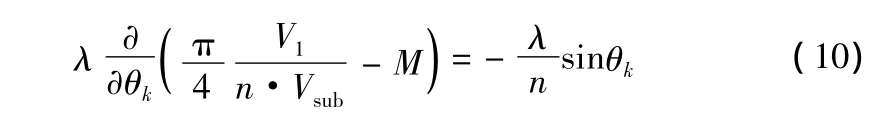
根据式(9)、(10)可以将式(5)转换为:

设定一个系数ρ，表示为:

由式(11)ρ又可表示为:

只要获得ρ就可以得到第k个电平的触发角θk，不用考虑阶梯数。根据高次谐波为0的目标建立含ρ的方程φ(ρ):

这样ρ的第k次迭代值可以用式(16)表示:

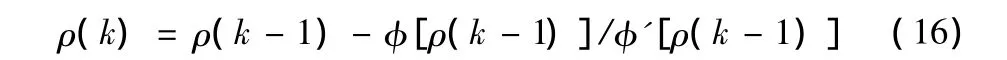
通过仿真验证，ρ在很少的迭代次数内就可以得到最优解［9］，计算速度超过其他常用方法。

2 阶梯波调制范围

确定阶梯波调制策略后，还需要了解调制的有效范围，包括不同阶梯电平数和调制比M以及谐波含量的对应关系［11］。

图2 触发角变化趋势

M 取0.65 ～ 1.05，阶梯电平数n分别选7和 6，触 发角和调制比的对应波形如图2所示。从图2中看出在在M＜0.73时，各触发角保持不变，说明调制策略已经失效，调制结果不可取;在M为1时，各触发角相同，说明波形为方波，调制结果也不可取。

再分析调制结果的谐波含量，在上述范围内选取了4个不同的M，对其输出波形进行傅立叶分析，结果如表1所示。

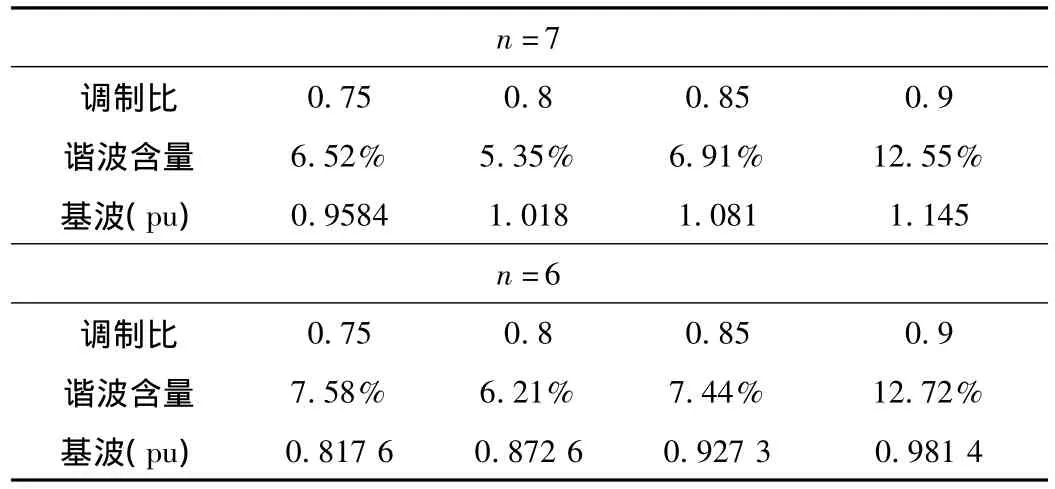
表1 不同调制比下的谐波含量

从表1看出，调制比过大时，谐波含量也较大，合理范围为0.75－0.85之间。

3 混合调制策略

由分析可知上述方法的调制范围较小，为扩大调制范围，首先须实时改变电平数量，但电平数过少时，就只有采用PWM调制［12］。无论改变电平数，还是改变调制方法，都要考虑输出电压的平滑切换。

变流器交流电压和直流电压的关系为:

式中μ是直流电压利用率;Ud是直流端电压。μ是影响交流电压幅值的因素，而不同电平数的阶梯波调制以及PWM调制的直流电压利用率是不同的。对于7电平和6电平阶梯波的直流电压利用率还无法确切知道，这里根据表1的波形分析结果进行估算，由于7电平时基波标幺值和调制比的比值基本在1.272附近，可以认为它的μ为1.272;同理认为6电平时的 μ为1.09。而多重PWM调制可近似认为是1。根据这些分析，可以画出混合调制的示意图如图3所示。

图3 7电平MMC的混合调制模式

图中 μ1为 1/1.272，μ2为 1/1.09，μ3为 1，为避免切换过程产生振荡，在判断环节中加入滞环。

4 仿真

目前MMC在可再生能源的传输和并网领域应用广泛，因此电网对MMC的性能也提出了严格要求。为了最大限度的发挥并网变流器的作用，要求变流器在有功功率很低时，能够输出较大的无功功率。另外，瞬间接地也是大电网常见故障，要求并网变流器不会出现脱网的情况。下面对采用混合调制策略的MMC在这些工况下的表现进行仿真验证。仿真的对象是一个小型风场通过MMC-HVDC(high voltage direct current)传输并网的系统，风场以及发送端用电流源和并联电容代替，并网端为7电平的MMC，仿真系统结构框图用图4表示。

图4 仿真模型

仿真参数为，风场额定功率为18 MW，直流传输电压为±30 kV，并网变压器为Δ/Y接法，阀侧额定电压为37 kV，网侧额定电压为120 kV。

仿真1:设风场的传输功率为0.5 pu，并网端的对电网的无功功率输出为－0.5 pu，在3 s时，MMC控制的无功指令跳变到1.0 pu，图5给出了跳变前后的无功功率、a相上桥臂电压、电网电流的波形，从图中看出随着无功功率变化，a相上桥臂电压从7电平变化为6电平，证明阶梯波调制模式的切换很好的扩大了调制比的范围，PCC点电流波形也说明两种调制模式都能保证良好的电能质量。

图5 无功功率跳变情况

仿真2:设风场的传输功率为1.0 pu，并网端的无功功率输出为 －0.5 pu，在3 s时，PCC 点发生0.12 s接地，图6 给出了接地前后的电网电压、调制比、a相上桥臂电压、电网电流的波形，从图看出电网电压跌落后，调制比的指令也迅速跌落，桥臂电压变化成脉冲波形式，MMC输出电流幅值也保持了基本稳定，证明MMC在进行低电压穿越时有效的实现了低电压输出，保护了功率器件安全。

图6 低电压穿越情况

5 结束语

本文以应用于可再生能源并网的MMC为例，分析并验证了阶梯波和PWM混合调制的控制方法，并得到以下结论:

(1)基于拉格朗日乘子法的阶梯波调制法很好的解决了电平数较多时计算负担过重的问题，但其具有调制范围较窄的缺陷;

(2)通过对不同电平数的阶梯波调制进行切换，可以解决调制范围小的问题，但在切换时要考虑到直流电压利用率的差别;

(3)MMC并网端在电网接地故障时必须要采用PWM调制，才能实现低电压输出以保障设备安全。

［1］A LESNICAR，R MARQUARDT.An innovative modular multilevel converter topology suitable for a wide power range［C］.Power Tech Conference Proceedings，2003 IEEE Bologna，2003(3):6.

［2］ DANIEL SIEMASZKO， ANTONIOS ANTONOPOULOS， KALLE ILVES，et al.Evaluation of control andmodulationmethods formodular multilevel converters［C］.2010 International Power Electronics-ECCE Asia-， IPEC 2010， Sapporo， Japan:Association for Computing Machinery，2010:746 －753.

［3］ B GEMMELL，JDORN，D RETZMANN，et al.Prospects ofmultilevel VSC technologies for power transmission［C］.Transmission and Distribution Conference and Exposition，2008.T＆D.IEEE/PES.2008:1－16.

［4］ L.-E JUHLIN，T LARSSON，J SKANSEN，et al.Considerations regarding RI limits for high voltage HVDC or FACTS stations［C］.CIGRE 2006，PARIS.

［5］ LIQIANG，HE ZHI-YUAN，TANG GUANG-FU.Investigation of the harmonic optimization approaches in the new modular multilevel converters［C］.2010 Asia-Pacific Power and Energy Engineering Conference，APPEEC － 2010，Chengdu，China:IEEE Computer Society.Q.

［6］ ZHENG CHUN-FANG，ZHANG BO，QIU DONG-YUAN.Selective harmonic elimination technique based on walsh transform for multilevel inverters［J］. Diangong Jishu Xuebao/Transactions of China Electrotechnical Society，2006，21(7):121 －126.

［7］ FAETE FILHO，LEON M TOLBERT，YUE CAO，et al.Real-time selective harmonic minimization for multilevel inverters connected to solar panels using artificial neural network angle generation［J］.IEEE Transactions on Industry Applications，2011，47(5):2117 －2124.

［8］屠卿瑞，徐政，姚为正.模块化多电平换流器型直流输电电平数选择研究［J］.电力系统保护与控制，2010，38(20):33－38.

［9］ YU LIU，HOON HONG，ALEX Q HUANG.Real-time calculation of switching angles minimizing THD for multilevel inverters with step modulation［J］.IEEE Transactions on Industrial Electronics，2009，56(2):285－293.

［10］魏文辉，宋强，滕乐天，等.基于反故障控制的链式STATCOM动态控制策略的研究［J］.中国电机工程学报，2005，25(4):19－24.

［11］何大清.基于直流串联的海上风电场及其控制［D］.上海:上海交通大学，2013.

［12］ LIE XU，BJARNE R ANDERSEN，PHILLIP CARTWRIGHT.VSC transmission operating under unbalanced AC conditions-analysis and control design［J］.IEEE Transactions on Power Delivery，2005，20(1):427－434.

Hybrid Modulation Strategy for Modular Multi-level Converters

HE Da-qing
(Central Academy，Shanghai Electric Group Co.，Ltd.，Shanghai200070，China)

This paper briefly describes the application ofmodularmulti-level converters and the advantagesof step wavemodulation，analyzes the principle of step wavemodulation algorithm based on the Lagrangemultiplier，and points out the advantages of the algorithm over the multi-level calculation.It demonstrates the process of implementing the step wave calculation in the Newton-Larsson method，calculates its modulation range，and analyzes the harmonic component of the output voltage in the Fourier analysis method to determine the modulation range reasonably.Furthermore，in view of the disadvantage of narrow modulation range，it presents a control strategy using hybrid modulation of step waves of various levels and multiple carriers.The hybrid modulation strategy is verified through simulation of changes of the reactive power and low-voltage ride through of the 7-level converter.Finally it is concluded that hybrid modulation can remarkably improve the control ability of themodularmultilevel converter.

modularmulti-level converter;step wave;hybrid modulation;Lagrangemultiplier;Fourier analysis;low-voltage ride through

10.3969/j.issn.1000 －3886.2015.06.005

TM46

A

1000－3886(2015)06－0014－04

定稿日期:2014－12－08

上海市科委科技攻关计划(13dz1200401)

何大清(1973－)，男，湖南人，博士，主要研究方向为可再生能源并网。