乘积季节ARIMA模型的建立及其在河南省甲型病毒性肝炎发病数预测中的应用

李军，史鲁斌，肖占沛

河南省疾病预防控制中心，河南郑州 450016

甲型病毒性肝炎（甲肝）是由甲肝病毒引起的以肝脏损害为主的消化系统传染性疾病，主要经粪—口途径传播；随着甲肝疫苗预防接种的推广和卫生状况的改善，河南省甲肝的发病率逐年下降，但仍存在不同程度的甲肝流行以及局部地区的暴发[1]。传染病的流行状况往往受到经济水平、社会环境和生活方式、针对性的疫苗接种率等多种因素的影响。近几年来国内外有研究者[2-5]利用疫情监测数据构建ARIMA模型，预测传染病的发病趋势，取得较好的预测效果。该研究将利用河南省2008—2013年分月甲肝疫情监测数据建立ARIMA模型，并利用2014年的监测数据评价ARIMA模型的预测效果。

1 资料与方法

1.1 资料来源

疫情数据来源于中国疾病预防控制信息系统中河南省2008～2013年分月的甲肝监测数据。

1.2 研究方法

采样时间序列法，利用河南省2008—2013年分月的甲肝疫情监测资料，通过SAS 9.1统计软件，建立甲肝发病的ARIMA模型的多个模型，筛出最优模型，利用2014年1—12月的甲肝疫情资料评价该模型的预测效果。ARIMA模型分为自回归模型（AR)、移动平均模型（MA)、ARIMA模型[6]。

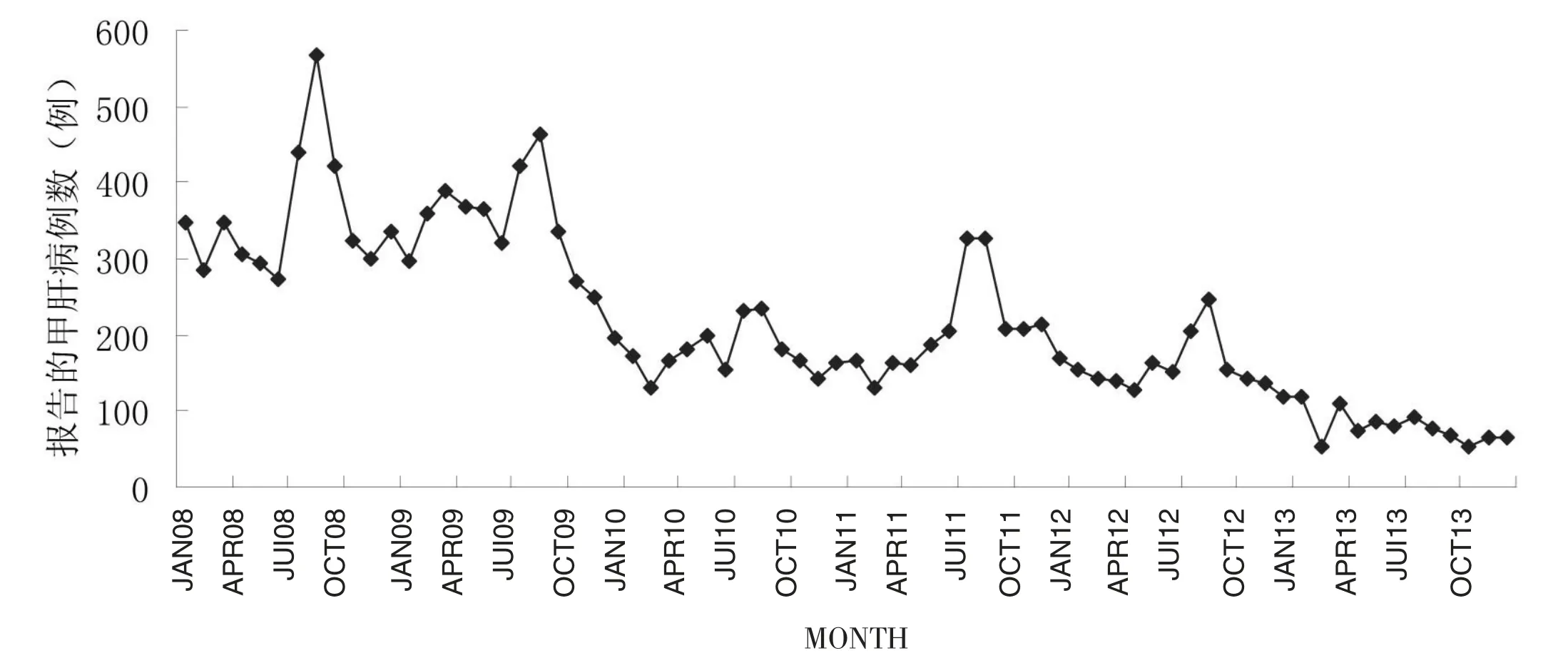
图1 2008—2013年河南省报告的甲肝病例数按月分布图

一般ARIMA建模包括模型的识别、参数估计、模型检验3个步骤，依据河南省2008—2013年甲肝分月的监测数据，通过这3个步骤反复建模，筛选出最优的预测模型。

①模型识别：观察2008—2013年甲肝分月监测数据的时间序列的平稳性，如若是非平稳序列，要通过数据转化和一阶周期为12的季节性差分将序列平稳化。先对序列的季节性成分进行分析，再识别非季节性成分，通过观察序列的自相关系数和偏相关系数初步确定阶值。

②参数估计：模型参数估计运用最大似然法或最小二乘法，根据序列的自相关系数和偏相关系数，经过不同方法的参数选择、比较、筛选，计算出自回归移动平均过程的系数，并对其标准误进行假设检验。

③模型检验：一个合适的模型的残差序列是白噪音过程，其自相关系数（autocorrelation function，ACF）和偏向相关系数（partial autocorrelation function，PACF）应与0无统计学差异，利用此标准对所建立的ARIMA模型是否合适作出诊断。若几个模型都能满足要求，选取Akaike信息准则 （Akaike information criterion，AIC）和Schwarz贝叶斯准则（Schwarz Bayesian information criterion，SBC）、残差序列的方差（Variance estimate，VE）以及方差估计的平方根（standard error estimate，std.EE）较小者，则模型效果较好[7]。

2 结果

2.1 河南省2008—2013年甲肝报告病例数的变化趋势

河南省2008—2013年甲肝报告病例数呈现明显的季节性，每年的6～9月呈现发病高峰，11月至次年3月呈现发病低谷，且呈现逐年递减趋势，提示该时间序列为非平稳序列。2008—2013年河南省报告的甲肝病例数按月分布情况见图1。

2.2 模型识别结果

在对原始数据进行对数转换的基础上进行了一阶差分和一阶周期为12的季节性差分，将序列平稳化，生成数据系列（图2），图2的图形显示差分后序列近似平稳。延迟1阶和12阶的自相关系数显著大于可信区间范围，说明差分后仍具有短期相关性和明显的季节性，考虑拟合ARIMA乘积季节模型。

2.3 参数估计结果

经过参数比较和选择，根据AIC和SBC的最小的准则和模型简洁原则，初步判断为模型ARIMA(1,1,0)(2,1,2)，见表1。

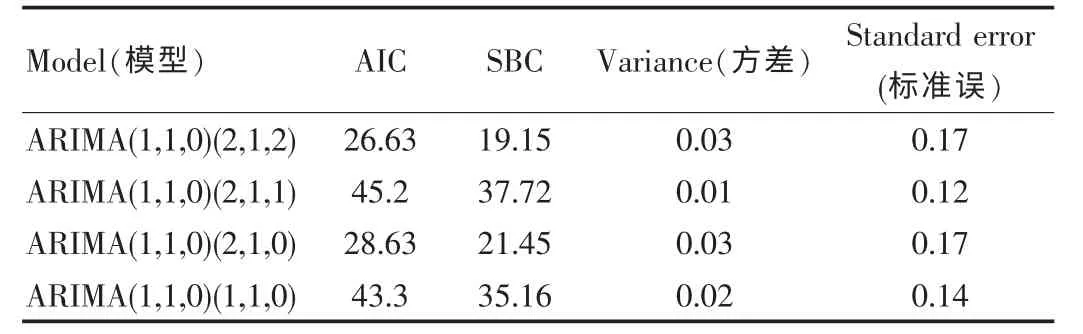
表1 各模型的拟合优度统计量

2.4 模型的检验结果

模型ARIMA(1,1,0)(2,1,2)延迟6阶、12阶、18阶、24阶、30阶、36阶X2检验统计量的P均＞0.05，表明模型对数据信息提取充分，拟合效果较好，见图3。

3 讨论

某地甲肝的暴发流行与当地的经济、卫生、甲肝疫苗接种等有关。由于受诸多因素的影响，甲肝暴发或者流行的早期预警尤为重要。

传统的甲肝预测预警模型可以分为两类：回归分析模型和时间序列模型。前者由于受到各种未知因素的影响、难以获得足够的数据进行分析，因此有一定的局限性。后者将已知的、未知的因素综合成一个统一的因素，将这些因素蕴含在时间序列这个变量中，所需的原始资料较少，对疾病短期内的预测效果较好，具有一定的应用前景[8-10]。

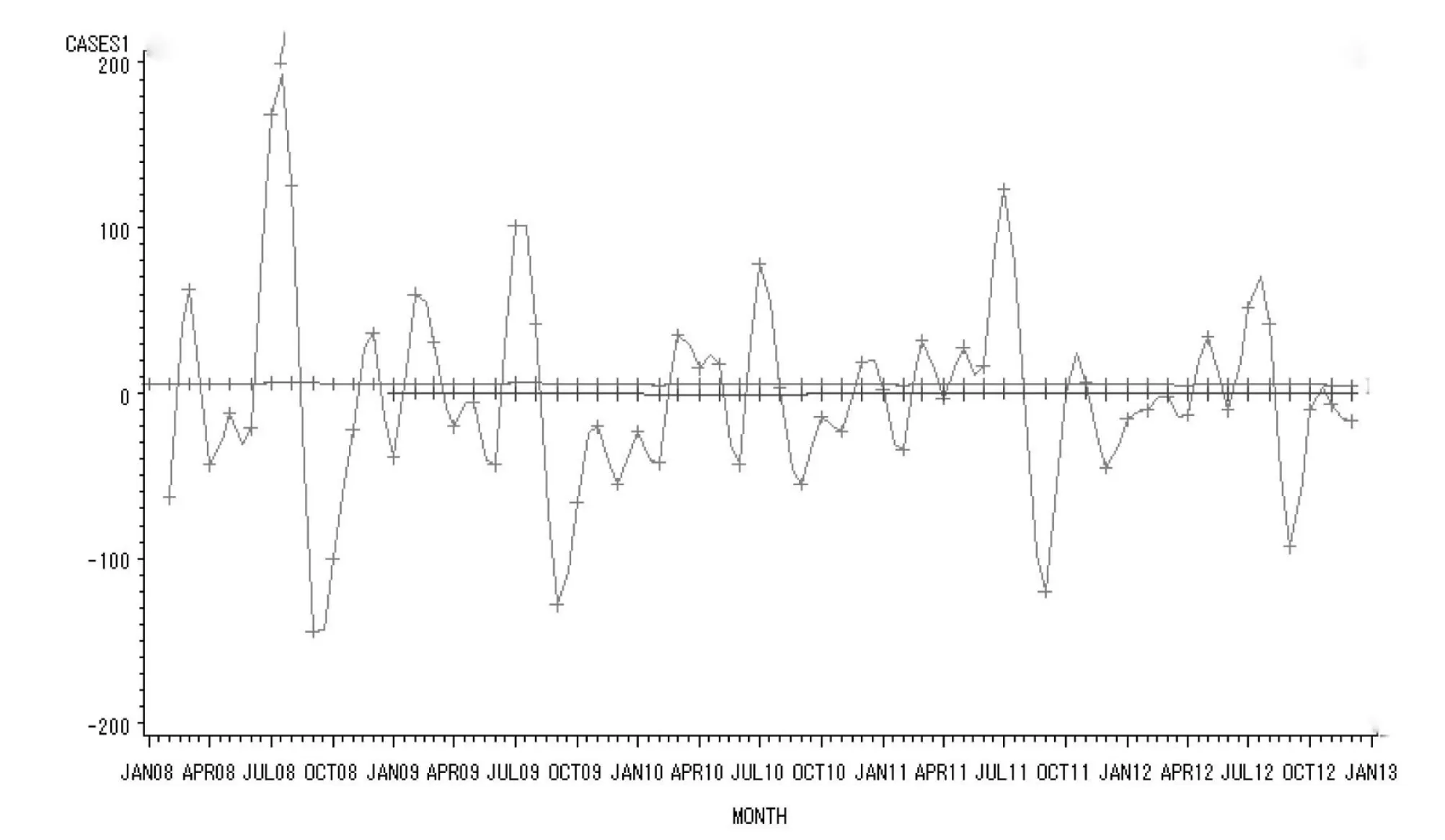
图2 1阶与12步差分和对数转换后序列图

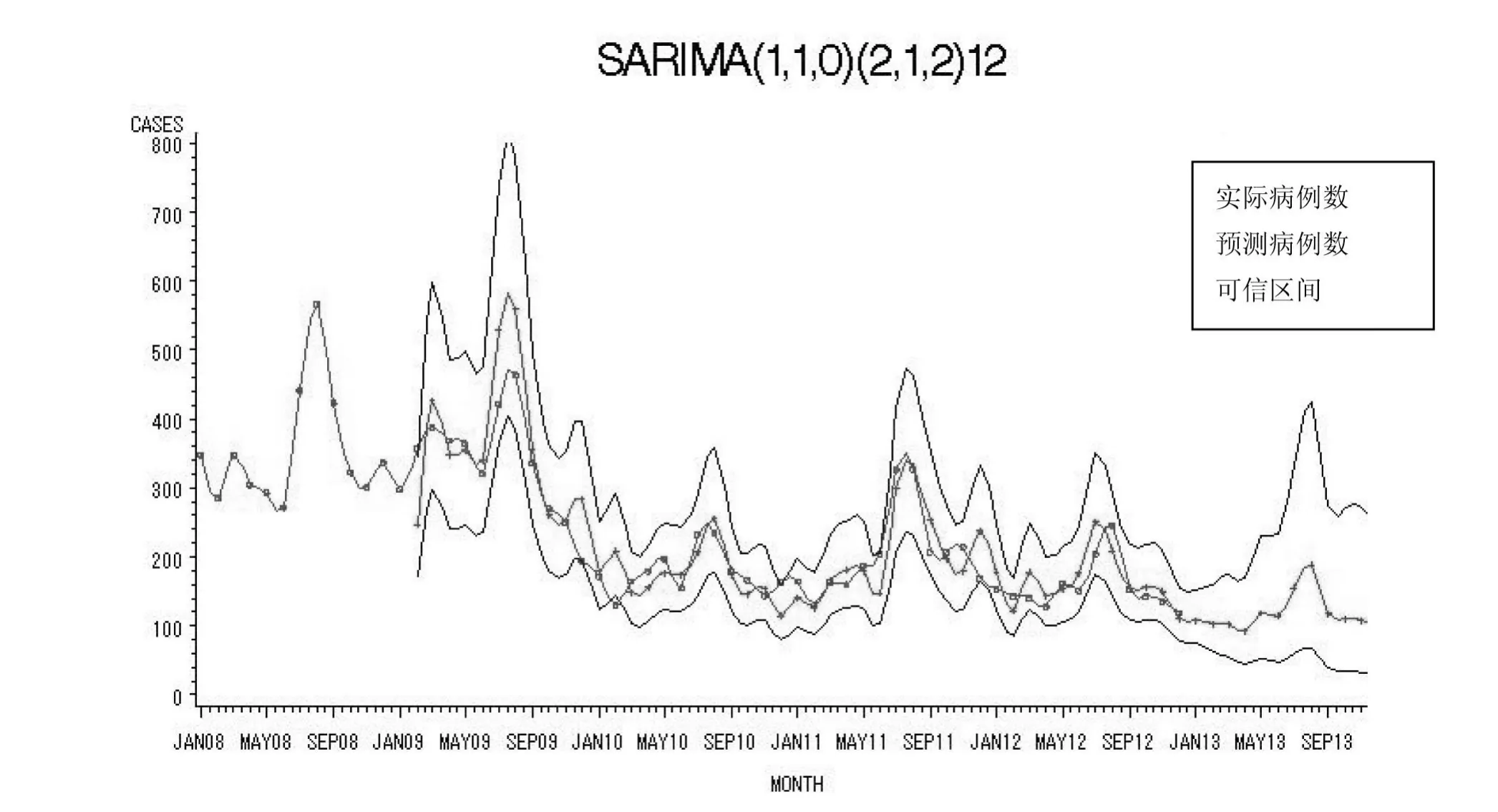
图3 河南省甲肝按月报告病例数的拟合效果图

该研究对河南省2008—2013年的甲肝监测数据资料进行拟合建模，结果显示，河南省2008—2013年的甲肝监测数据呈现逐年降低的趋势，且具有明显的季节性周期。筛选ARIMA（1，1，0）（2，1，2）12模型为最优模型，利用此模型对2014年1—12月的甲肝监测数据进行预测，结果显示预测值与真实值接近，提示该模型有较好的预测效果，在河南省甲肝发病预测中具有较高的推广应用价值，可为河南省甲肝的防控措施及预警机制提供参考。

[1]朱奕奕，冯玮，赵琦，等.ARIMA乘积季节模型在上海市甲肝发病预测中的应用[J].复旦学报：医学版，2012,39（5）：460-464.

[2]杨召，叶中辉，尤爱国，等.乘积季节ARIMA模型在结核病发病预测中的应用[J].中国公共卫生，2013,29（4）：469-472.

[3]彭志行，鲍昌俊，赵杨,等.ARIMA乘积季节模型及其在传染病发病预测中的应用[J].数理统计与管理，2008,27（2）：362-368.

[4]金如锋，邱红，周霞,等.ARIMA模型和GM(1，1)模型预测全国3种肠道传染病发病率[J].复旦学报：医学版，2008,35（5）：675-680.

[5]时照华，苏虹，秦凤云,等.ARIMA模型在常见呼吸道传染病疫情预测中的应用[J].安徽医科大学报，2013,48（7）：783-785.

[6]黄春萍，邓晶，张磊,等.ARIMA模型在麻疹预警中的应用[J].疾病监测，2008,23（1）：53-55.

[7]李永红，林枚，董柏青,等.ARIMA模型在细菌性痢疾预测中的应用[J].现代预防医学，2010,37（7）：1203-1204.

[8]叶孟良，李智涛，欧荣.ARIMA模型在预测重庆市医院日住院量中的应用[J].重庆医学，2012,41（13）：1260-1261.

[9]牟瑾，谢旭，李媛,等.将ARIMA模型应用于深圳市1980-2007年重点法定传染病预测分析[J].预防医学论坛，2009,15（11）：1051-1052.

[10]张彦琦，唐贵立，王文昌,等.ARIMA模型及其在肺结核预测中的应用[J].现代预防医学，2008,35（9）：1608-1612.