连续梁倒拆施工倾覆稳定性的体系可靠度方法

马如进，李忠鹏

（同济大学 土木工程学院，上海200092）

当前我国现有桥梁病害发展严重，设计荷载不满足当前交通运输需要，更有河道桥梁不满足通航要求，亟需改建扩建，因此桥梁拆除问题是桥梁工程师即将面临的重要课题.

桥梁拆除方法有控制爆破拆除、静力爆破拆除和机械拆除等等.在机械切割拆除施工过程中存在很多不确定性，施工安全性较难控制.2012年7月，杭州幸福路跨线桥拆除过程中坍塌，事故原因为拆除过程中吊机的一根吊索断裂，导致桥梁坍塌.可见现有桥梁拆除施工作业存在一定的盲目性，缺少完备的安全评价体系支撑，容易导致安全事故发生.

针对混凝土连续梁的机械倒拆拆除研究较少.刘成章［1］针对预应力混凝土连续梁的拆除进行了拆除方法的讨论和拆除结构的受力及变形分析和设计验算.张维昕［2］等人就连续梁顶推拆除进行了仿真分析，文章分析了顶推拆除过程的受力和挠度变化.上述研究主要从桥梁拆除方法出发，研究拆除过程中结构受力和变形的发展特性，没有考虑桥梁拆除过程潜在的稳定性和风险性.桥梁拆除相对于正装施工，不确定性更大，但是正装施工中存在的双悬臂梁倾覆稳定性，也是桥梁拆除过程中的重要问题.而且拆除施工中存在箱梁切割误差导致的不平衡重力差，使倾覆稳定性问题更加突出.针对双悬臂施工倾覆问题，张建仁［3］对预应力混凝土箱梁悬臂施工状态进行了倾覆稳定性可靠性分析；Juan R C［4］用基于可靠度的方法提出了混凝土桥梁悬臂施工的分项安全系数；李生勇［5］分析了曲线梁桥最大悬臂施工状态下的可靠性.但以上研究均没有考虑桥梁施工偶然荷载工况造成的倾覆稳定性.本文重点研究施工过程中，吊索断裂破坏造成吊卸箱梁节段下坠引起双悬臂梁丧失倾覆稳定性，以及挂篮失效造成挂篮和吊卸箱梁节段下坠引起双悬臂梁倾覆的体系可靠度问题.

对于可靠度研究，构件可靠度的发展已日渐成熟，然而对于体系可靠度的计算却很难找到普遍认可的快速准确的方法.目前对体系可靠度的求解主要采用串并联模式分析，然而当一个失效元发生引起另一个失效元发生的概率大大增加时，两个失效元之间的关系已不再是简单的串联或并联关系.在串并联模式分析大型复杂系统时，通过相关系数求两交事件的概率，主要采用估计的方法忽略多事件间交事件的概率，因此该方法精度低、效率低.现今对于体系可靠度的计算，比较被人们接受的有宽界限法、窄界限法和概率网络法（PNET）.其中Ditlevsen提出的窄界限法仅对于结构相对简单，失效模式相对较少的体系具有较好的适用性；概率网络法较普遍地运用在大型复杂系统中，但是其临界相关系数的确定缺少理论依据［6］.

本文提出因果链模式的体系可靠度分析方法，并推导出其拓展的全概率公式计算方法.使用该方法和公式求得了双悬臂梁纵向倾覆稳定性的体系可靠度，和串并联模式多元函数积分法得到的结果比较显示，该方法可以更快速准确地计算体系可靠度.文中进一步给出贝叶斯公式法用于分析体系中最主要的失效模式，并对最主要的失效模式进行了参数敏感性分析.

1 体系可靠度因果链模式法

因果链模式法区别于体系串并联模式的重要条件是一个事件的发生会导致另一个事件发生的概率显著增大.

图1 因果链失效路径Fig.1 Causality-chains failure paths

失效路径如图1所示的失效模式中，A1，A2事件的发生会导致事件E发生的概率大大增加.如Robert在文献［7］中指出，失效模式A1—E中的两个失效元不是简单的并联模式，而是因果链模式，但书中并未给出因果链模式的体系可靠度计算方法.本文提出拓展的全概率公式解决方法.

当假设A1，A2可能同时发生时，则不能满足全概率公式中两两不相容的条件，为此本文对全概率公式的应用范围进行了推导拓展.

事件A1，A2分成两两不相容的4个事件，如图2所示，事件B1为，B2为，B3为A1∩A2，B4为，由此B1，B2，…，B4两两不相容，满足全概率公式的适用条件.因此得到因果链模式的体系失效概率公式为

由公式（1）可以看出，在因事件A1，A2相互独立时，因果链模式求体系失效概率不必求不同失效模式间的相关系数，也无需通过忽略多事件的相交概率估算体系失效概率.

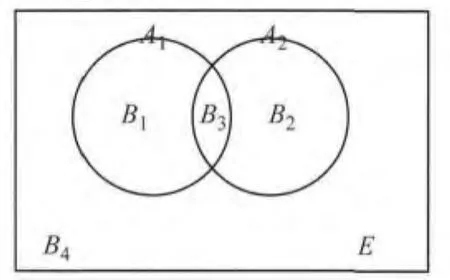
图2 全概率关系图Fig.2 Relationship of total probability formula

2 工程背景

上海某国道待拆混凝土桥，主桥为56m+80m+56m三跨变截面预应力混凝土连续梁桥.由于该桥净空不满足通航要求需拆除，原址重建.拟定采用逆施工顺序，挂篮悬臂切割，倒拆施工拆除.拆除施工过程中最不利工况为最大双悬臂挂篮吊卸过程，如图3所示.对此工况中的双悬臂倾覆稳定性进行可靠度研究.待拆桥梁实景图如图4所示.待拆桥梁横断面图如图5所示.

3 体系中失效元的可靠度

3.1 失效因素

预应力混凝土连续梁桥双悬臂挂篮施工纵向倾覆破坏是指双悬臂梁在不平衡荷载产生倾覆力矩大于抗力矩时纵向整体倾覆垮塌.如图3所示，引起纵向倾覆的荷载工况有施工切割不对称重力差、施工活荷载差、施工过程风压差，以及最不利的荷载工况（吊索下放节段突然坠落、挂篮突然失效坠落引起的自重差）.本算例中，挂篮结构承载失效的失效概率远低于挂篮前支点主梁混凝土承压失效概率，为简化计算，本文以挂篮前支点承压失效作为挂篮失效的计算依据.影响纵向倾覆稳定性的变量参数主要有：箱梁自重、施工活荷载差、施工过程不均匀风荷载、临时支撑的抗力、箱梁切割误差、吊索抗力、挂篮前支点混凝土局部承压抗力等.

图3 最大双悬臂拆除示意图Fig.3 Cantilever demolition in the longest cantilever state

图4 待拆桥梁实景图Fig.4 Picture of the bridge to be demolited

图5 桥梁横断面图（单位：mm）Fig.5 Cross section of the bridge（unit：mm）

3.2 概率模型

对于混凝土承压抗力的概率模型，牛荻涛等人［8］在总结国内外实验和实测的基础上，用非平稳正态随机过程描述现役混凝土结构的强度历时变化规律，利用统计回归方法提出混凝土强度变化的概率模型.本文使用该方法计算得到服役桥梁混凝土强度的概率模型，强度平均值和标准差分别为

式中：mco和σco分别为混凝土28d强度的平均值和标准差.其中

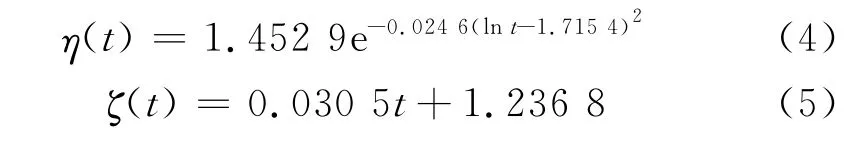
本工程中时间t为17年，结合规范［9］得到C50混凝土28d抗压强度设计值的平均值为23.15 MPa，变异系数为0.050 9.

对于吊索抗力的概率模型，假定施工选择直径为26mm的纤维芯钢丝绳，考虑选用钢丝绳的新旧程度，乘以一个安全系数.则吊索抗力的均值为μfk=0.6R0，变异数V=0.081 9，服从正态分布，R0为钢丝绳公称抗拉强度.结合实际情况，计算和选定的桥梁纵向倾覆稳定性的参数概率模型如表1.

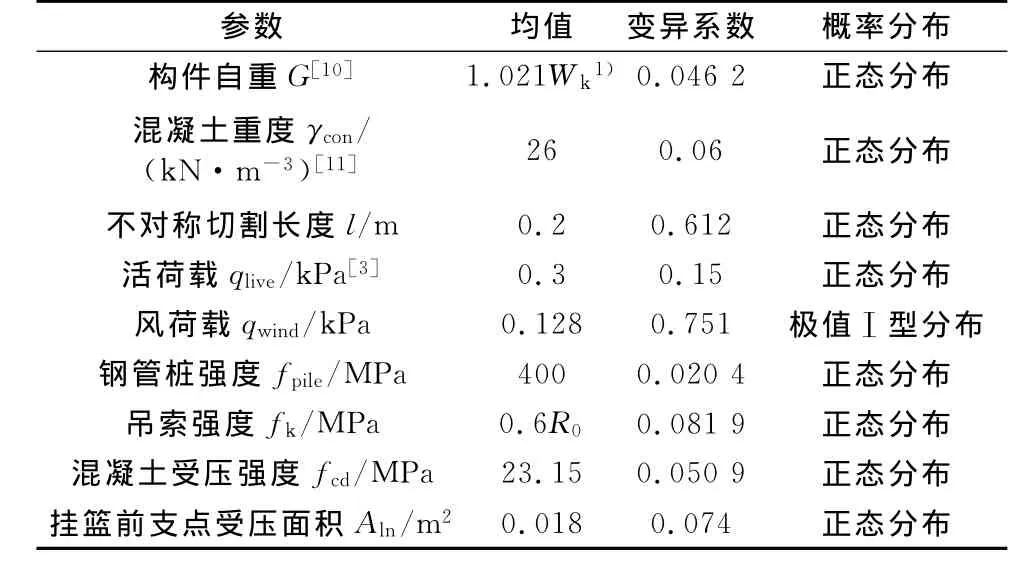
表1 纵向倾覆稳定性参数概率模型Tab.1 Probability model for longitudinal overturning stability parameters

3.3 失效元可靠度分析

设事件E为纵向倾覆稳定性丧失；事件E1为吊索破坏造成节段下坠引起纵向倾覆，事件E2为挂篮失效造成挂篮和节段下坠引起纵向倾覆，事件E3为不平衡恒荷载和活荷载引起纵向倾覆；事件E11为吊索破坏失效，事件E12为节段下坠引起纵向倾覆；事件E21为挂篮前支点混凝土局部承压失效，E22为挂篮、节段同时下坠引起纵向倾覆.失效路径如图6所示.

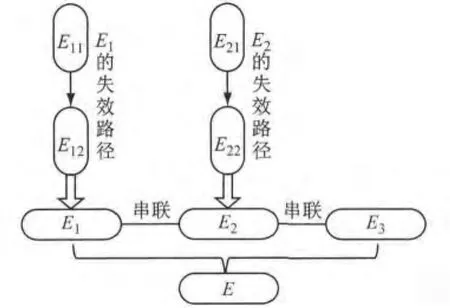
图6 失效路径图Fig.6 Failure paths of the system

对于每一个失效事件，采用一次二阶矩方法计算其可靠指标和失效概率，并求得交事件间的相关系数.对于交事件的失效概率，采用对多元正态分布函数积分得到，结果如表2和表3.

表2 失效元的可靠指标和失效概率Tab.2 Reliability index and failure probability of failure elements

表3 交事件的相关系数及失效概率Tab.3 Correlation coefficient and failure probability of intersection events

从表2可以看出，E12和E22的失效概率都明显大于E3的失效概率，结合力学分析可知，吊索失效E11和挂篮失效E21的发生会导致悬臂梁纵向稳定性显著降低.表3结果在串并联模式方法验证时选用.

4 纵向倾覆稳定性体系可靠度

4.1 因果链模式法

将前文提出的因果链模式法的全概率公式，应用到本工程中，E11和E21分别对应图1和图2中的A1和A2.公式（1）中的B1为，B2为E21∩，B3为E11∩E21，B4为.公式（1）变量在本工程实际中的意义为：B1为吊索断裂破坏而挂篮完好；B2为挂篮失效，而吊索完好；B3为挂篮和吊索都失效；B4为挂篮和吊索都完好.

由表2计算全概率公式中各事件的失效概率，如表4所示.

表4 拓展的全概率公式中各事件的概率Tab.4 Probability in developed total probability formula

将表4的结果带入计算公式（1），得到双悬臂梁纵向倾覆的失效概率为Pf（E）=1.05×10-24，对失效概率进行标准正态分布逆累积分布函数计算，即得到可靠指标β=10.19.

4.2 串并联模式法比较

如果用传统的串并联模式方法，则在串并联模式中纵向失稳事件E由3种失效模式E1，E2，E3串联而成.失效模式E1由失效路径E11—E12组成，E11和E12并联；失效模式E2由失效路径E21—E22组成，E21和E22并联.串并联形式可以在图6的失效路径图中直观地看出.E11，E21分别与其余事件两两相互独立.

根据串并联模式的概率理论给出该体系的计算公式

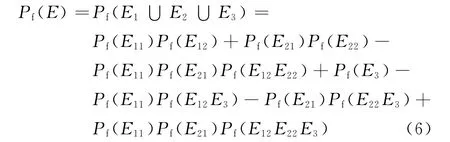
将表2、表3中的计算结果代入式（6）得Pf（E）=1.05×10-24，可靠指标β=10.19.与因果链模式法采用拓展的全概率公式计算得到的结果相吻合，验证了因果链模式法的正确性.但是从公式（6）中可以看出，串并联模式法需要计算交事件的E12∩E22，E12∩E3和E12∩E22∩E3的概率，若要得到准确的结果，只能逐一求出两两事件的相关系数并通过积分方法求得失效概率，而当系统增加3个失效元如E31，E41，E51或更多时，就要积分求56个交事件的概率，计算效率低下；另外，快速的方法只有通过界限法求得近似失效概率，但准确率低.从公式（1）和全概率公式关系图2可以看出，不管增加多少个因事件失效元，只要因事件失效元间相互独立，即不需要复杂的积分方法求交事件的失效概率，仅通过全概率公式图即可快速写出体系可靠度的失效概率公式并快速求解.

5 参数敏感性分析

5.1 引起体系失效最主要的原因失效模式

为了分析体系失稳中占主导作用的失效模式，基于因果关系联接模式方法，本文引入贝叶斯公式方法分析主要失效模式中最重要的失效模式.

由于本文中E11和E21相容，仍然不能直接使用贝叶斯公式，同样如图2所示，将E11和E21分别分成互不相容的B1，B3事件和B2，B3事件.其中

如此可应用拓展的贝叶斯公式求得各主要失效模式中最重要的失效模式.计算分析得到如果纵向倾覆发生，各种失效模式的贝叶斯概率如图7.可见，如果双悬臂梁纵向倾覆，则最有可能的原因是吊索断裂破坏造成箱梁节段下坠引起，其次是挂篮失效造成挂篮和箱梁节段下坠引起.而这两种失效模式共同发生的概率很低，倾覆由不平衡恒载和活载引起的概率也很低.因此应当重点防范吊索断裂和挂篮失效.

图7 主要失效模式的贝叶斯概率Fig.7 Bayes probability of main failure modes

5.2 吊索失效参数敏感性分析

针对吊索破坏造成吊卸箱梁节段下坠引起倾覆的较大贝叶斯概率问题，本文对吊索破坏失效元进行了参数敏感性分析.吊索断裂破坏的功能函数为

式中：f为钢丝绳吊索的抗拉强度；G为吊卸混凝土箱梁节段的重力；A为钢丝绳吊索断面面积.

变量中节段箱梁自重由挂篮的吊装能力和悬浇节段决定，吊索的抗拉强度和面积可以人为选择控制，本文对此进行了敏感分析，结果如图8和图9所示.其中吊索的抗拉强度为钢丝绳的公称抗拉强度乘以一个老旧系数.老旧系数平均值取0.6，钢丝绳公称抗拉强度参照《重要用途钢丝绳（GB 8918—2006）》选取［12］.

图8 吊索强度选择敏感性分析图Fig.8 Senstivity analysis of lifting rope strength parameter

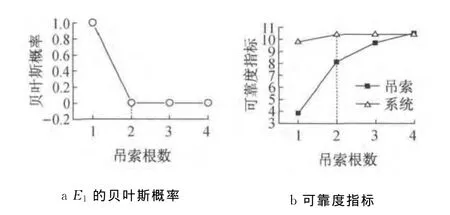
图9 吊索根数强健性分析图Fig.9 Robustness analysis of the number of lifting ropes

首先依据规范［12］选定钢丝绳直径为26mm，对吊索抗拉强度作敏感性分析，发现随着选用拉索抗拉强度的提高，吊索的可靠指标和体系倾覆稳定性的可靠指标有所提高.当选用抗拉强度为1 062MPa的钢丝绳时，吊索和系统可靠指标随抗拉强度提高而增大不再明显，而且体系失效的主要原因也不再是由吊索失效引起的.

假定施工方选用了抗拉强度最低的钢丝绳，钢丝绳吊索的抗拉强度均值为942MPa.为确保吊索安全性，需增加吊索的根数，本文即对吊索根数作了强健性分析，假定每根钢丝绳的直径为26mm.从图9中可以看出，随着吊索根数的增加，吊索和系统的可靠度指标显著增加，当采用吊卸箱梁节段每侧2根，总共4根吊索时，体系失效的主要原因即已不再由吊索失效引起，体系倾覆稳定性的可靠指标为10.42，失效最主要的原因是由挂篮失效引起，其贝叶斯概率为1.

5.3 挂篮失效参数敏感性分析

针对挂篮破坏造成吊卸箱梁节段和挂篮下坠引起倾覆较大的贝叶斯概率问题，本文对挂篮失效元进行了参数敏感性分析.挂篮前支点处混凝土局部承压功能函数为

式中：ηs为混凝土承压修正系数；β为混凝土局部承压强度提高系数；fcd为混凝土抗压强度设计值；Aln为混凝土局部承压面积；Fld为局部压力设计值.fcd由服役期混凝土材料性能决定，Fld由挂篮和下放节段重力决定，这其中只有Aln可以人为控制.结合上文分析结论，在吊卸节段箱梁吊索采用2根的最小抗拉强度的基础上，本文对挂篮前支点混凝土局部受压失效问题进行了敏感性分析，结果见图10.

图10 挂篮前支点混凝土承压面积敏感性分析Fig.10 Concrete pressure-bearing area sensitivity at the hanging basket fore-support point

从图中可以看出增加挂篮前支点混凝土承压面积可以使挂篮和系统的可靠指标增大.但是从E2事件的贝叶斯概率可以看出，即使挂篮的可靠指标达到10，双悬臂梁系统失稳的主要原因仍然是由挂篮失效引起的.由贝叶斯公式可以推测，这是因为在挂篮失效发生的条件下，双悬臂梁倾覆稳定性失效概率很大，可靠指标很低.

5.4 挂篮失效条件下主梁倾覆参数敏感性

针对在挂篮失效发生的条件下双悬臂梁的失稳事件E22可靠指标很低的问题，本文对其进行了参数敏感性分析.挂篮失效条件下主梁倾覆事件的功能函数为

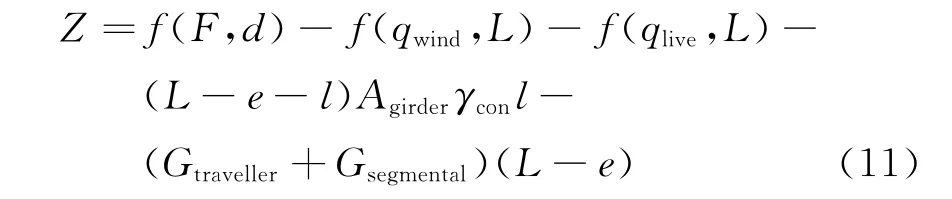
式中：F为钢管桩临时支撑抗力；d为临时支撑至倾覆点的距离；qwind为风荷载；L为双悬臂梁一侧梁段距离；qlive为施工活荷载；l为箱梁切割长度误差；Agirder为箱梁面积；γcon为混凝土重度；Gtraveller和Gsegmental分别为下坠挂篮和箱梁节段的重力；e为墩顶中心至悬臂梁倾覆点的距离，取0.75m.

功能函数中，风荷载和施工活荷载由统计分析获得，箱梁长度、截面积（切割翼缘的面积）和混凝土重度也基本不可控制.只有通过控制临时支撑抗力矩和箱梁切割误差来增大主梁稳定性.本文针对此两种变量作了参数敏感性分析，如图11和图12所示.其中钢管桩的屈服强度按《结构用无缝钢管选取（GB／T 8162-2008）》［13］.功能函数中的d按施工方案选定.

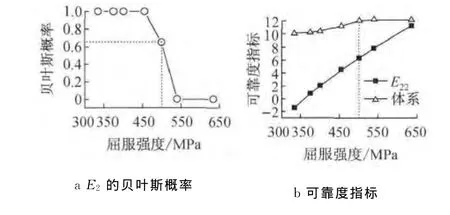
图11 临时支撑钢管桩强度敏感性分析Fig.11 Sensitivity analysis of temporary supports strength

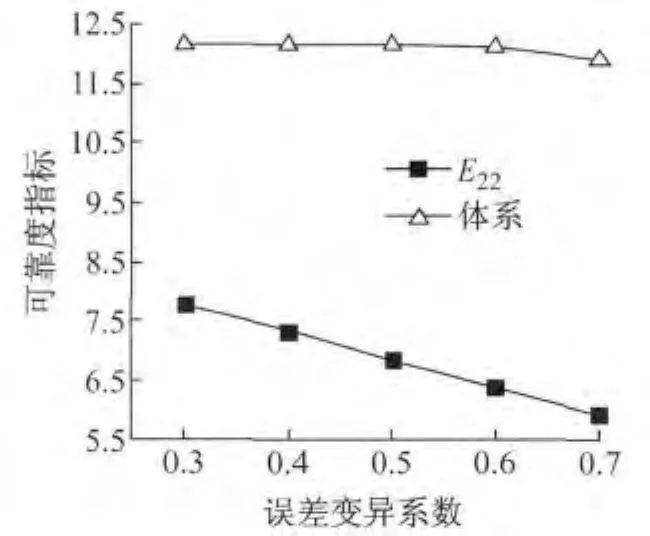
图12 箱梁切割误差敏感性分析Fig.12 Sensitivity analysis of box girder cutting error

从图11中可以看出，随着临时支撑钢管桩屈服强度的提高，挂篮失效条件下，E22的可靠指标明显提高，而系统可靠指标则在钢管桩屈服强度达到500 MPa后不再继续提高，原因可以在E2的贝叶斯概率变化趋势图中清楚得到.在钢管桩屈服强度达到500MPa以后，系统失效的原因已经不再全部由挂篮失效引起，而当钢管桩屈服强度达到540MPa时，体系失效的原因已几乎和E2无关.当采用500MPa的钢管桩时，体系失效的条件下，E1失效的概率为0.34，E2失效的概率为0.65.此时吊索抗力、钢管桩抗力、混凝土承压面积刚好匹配，没有过剩的材料强度；如果选用屈服强度小于440MPa的钢管桩，施工方案中的临时支撑桩与主墩的距离需要增大，否则不满足可靠度要求.

当采用500MPa屈服强度的钢管桩时，分析箱梁切割误差对倾覆稳定性的影响.

从图12可以看出，在挂篮失效条件下，随着切割误差变异系数的增大，主梁倾覆稳定性可靠指标显著降低；而系统可靠指标当切割变异系数在0.5以内时，基本没有变化；当变异系数超过0.5并逐渐增大时，系统可靠度也会明显减小.为此建议施工方控制箱梁切割误差变异系数在0.5以内.

6 结论

（1）提出了分析体系可靠度的因果链模式法，推导拓展了全概率公式的应用范围，并用拓展公式给出了因果链模式体系可靠度的计算公式.使用该公式计算得到双悬臂梁倒拆施工纵向倾覆稳定性的可靠度和失效概率.计算结果显示和串并联模式中多元函数积分得到的结果能够很好地吻合.

（2）拓展了贝叶斯公式的应用范围，并采用拓展的贝叶斯公式分析了体系失效条件下最易发生的失效模式.结果显示，双悬臂梁纵向倾覆稳定性失效最主要的原因是吊索断裂造成吊卸箱梁节段下坠引起以及挂篮失效造成挂篮和吊卸箱梁下坠引起.

（3）对最易发生的失效模式进行了参数敏感性分析，结果显示，吊索采用每侧2根，总共4根能较好地保证体系的可靠性；对于钢管桩临时支撑当采用抗拉强度小于440MPa时，宜增大临时支撑钢管桩到主墩的距离；箱梁不对称切割误差对体系可靠度影响较大，施工中应予以严格控制.

［1］ 刘成章.预应力混凝土连续箱梁桥拆除方法及其结构分析研究［D］.重庆：重庆交通大学，2012.LIU Chengzhang.Pre-stressed concrete continuous box girder bridge demolition method and structure analysis ［D］.Chongqing：Chongqing Jiaotong University，2012.

［2］ 张维昕，张凯，周鑫.连续梁桥顶推拆除过程的仿真分析［J］.中外公路，2013，33（1）：123.ZHANG Weixin，ZHANG Kai，ZHOU Xin.Simulation analysis of continuous bridge in incremental launching demolition process［J］.Journal of China &Foreign Highway，2013，33（1）：123.

［3］ 张建仁，许福友.连续梁桥悬臂施工整体稳定性可靠度分析［J］.长沙交通学院学报，2002，18（1）：26.ZHANG Jianren，XU Fuyou.Reliability analysis of continuous bridge integral stability in cantilever construction［J］.Journal of Changsha Communications University，2002 ，18（1）：26.

［4］ Juan R C.Reliability-based partial safety factors in cantilever construction of concrete bridges ［J］.Journal Structural Engineering，1997，123（3）：305.

［5］ 李生勇，张哲，黄才良，等.曲线梁桥最大悬臂施工状态下的可靠性分析［J］.武汉理工大学学报：交通科学与工程版，2008，32（3）：518.LI Shengyong，ZHANG Zhe，HUANG Cailiang，etal.Stability reliability analysis of a curved bridge in cantilever construction［J］.Journal of Wuhan University of Technology：Technology Science &Engineering，2008，32（3）：518.

［6］ 赵国藩，金伟良，贡金鑫.结构可靠度理论［M］.北京：中国建筑工业出版社，2000.ZHAO Guofan，JIN Weiliang，GONG Jinxin.Structure reliability theory［M］.Beijing：China Architecture &Building Press，2000.

［7］ Robert E M.Structural reliability analysis and prediction［M］.2nd ed.Chichester：John Wiley &Sons Ltd，1999.

［8］ 牛荻涛，王庆霖.一般大气环境下混凝土强度经时变化模型［J］.工业建筑，1995，25（6）：36.NIU Ditao， WANG Qinglin.Models of concretes strength changing with time in general air environment［J］.Industrial Construction，1995，25（6）：36.

［9］ 中国华人民共和国交通运输部.JTG D62-2004公路钢筋混凝土及预应力混凝土桥涵设计规范［S］.北京：人民交通出版社，2004.Ministry of Transport of the People's Republic of China.JTG D62—2004 Code for design of highway reinforced concrete and prestressed concrete bridge and culverts ［S］.Beijing：China Communication Press，2004.

［10］ 李杨海，鲍卫刚.公路桥梁可靠度与概率极限状态设计［M］.北京：人民交通出版社，1997.LI Yanghai，BAO Weigang.Reliability and probabilistic limit state design of highway bridge ［M ］.Beijing：China Communications Press，1997.

［11］ 田浩，陈艾荣，楼慧元.一种混凝土桥梁时变体系可靠度分析方法［J］.中南大学学报：自然科学版，2012，43（1）：346.TIAN Hao，CHEN Airong，LOU Huiyuan.An approach for evaluating time-variant system reliability of concrete bridges［J］.Journal of Central South University：Science And Technology，2012，43（1）：346.

［12］ 中华人民共和国国家质量监督检验检疫总局.GB 8918—2006重要用途钢丝绳［S］.北京：中国标准出版社，2006.General Administration of Quality Supervision，Inspection and Quarantine of the People's Republic of China.GB 8918—2006 Steel wire ropes for important purposes ［S］.Beijing：China Standard Press，2006.

［13］ 中华人民共和国国家质量监督检验检疫总局.GB／T8162—2008结构用无缝钢管［S］.北京：中国标准出版社.2008 General Administration of Quality Supervision，Inspection and Quarantine of the People's Republic of China.GB／T 8162—2008 Seamless steel tubes for structural purposes［S］.Beijing：China Standard Press，2008.