局部区域三维坐标变换的两步解法

胡 川，陈 义，2，朱卫东

（1.同济大学 测绘与地理信息学院，上海200092；2.同济大学 现代工程测量国家测绘地理信息局重点实验室，上海200092；3.上海海洋大学 海洋科学学院，上海200120）

将三维空间中的一系列点从一套坐标系（原系统）变换到另一套坐标系（目标系统）的行为称为三维坐标变换.要完成该行为首先需要建立变换模型.在测绘领域，布尔萨（Bursa-Wolf）模型，莫洛登斯基（Molodensky）模型和武测模型是比较常用的3种七参数小角度三维坐标变换模型［1-2］.具有大旋转角的三维坐标转换参数估计可以参考文献［3］.七参数是指3个平移参数，3个旋转参数和1个尺度参数.三维坐标变换的实质是通过一系列公共点和某种数学准则求取这7个变换参数的最佳值［4］.但变换的最终目的是求取非公共点在目标系统中的三维坐标.当公共点≥3个时，通常采用最小二乘法（least squares，LS）求解转换参数的最佳估计值.这种解法通常假设观测量的随机误差仅存在于目标系统的公共点中，而原系统中的坐标是准确已知的.事实上，原系统坐标也是通过观测计算得到的，其坐标也应该含有随机误差.用整体最小二乘法（total least squares，TLS）估计转换参数时同时顾及了两套坐标系统的误差［4-8］.尽管两套坐标公共点的误差得以消除，但是公共点与非公共点的相关性没有得到考虑.李微晓等［1］将最小二乘配置法引入到TLS平差中，使得当公共点与非公共点具有较强相关性时，坐标变换精度得到显著提高.但是该方法只考虑了系数矩阵的部分误差［9］，这种方法属于近似无缝坐标转换方法.针对该问题，李博峰提出了无缝三维基准转换模型［9-11］.无缝模型不仅考虑了上述相关性，而且顾及到了原系统中非公共点的误差.

在 应 用 GNSS （global navigation satellite system）技术建立各种小区域控制网时通常采用Bursa-Wolf模型进行三维变换.由于此时控制点分布范围较小，平移参数和旋转参数间存在较强的相关性使得解算模型病态［2］.文献［2］采用了只对平移参数正则化的病态最小二乘法（ill-posed least squares，ILS），提高了外围点的转换精度.此时，为顾及原系统的误差需要引入病态整体最小二乘法（ill-posed total least squares，ITLS）进行参数估计，但ITLS解算比较复杂.由于TLS的计算过程属于一个降正则化的过程，模型更容易出现病态问题，其解算比LS估计更不稳定［12-14］.因此，研究一种既能避免解算复杂ITLS问题又能提高变换精度的方法非常具有实际意义.

本文提出局部区域三维坐标变换的解算方法，该方法将旋转参数与平移参数和尺度参数分开计算，去除旋转参数与平移参数之间的相关性，避免解算复杂的病态TLS问题.旋转参数采用LS法进行解算，尺度和平移参数采用加权整体最小二乘法（weighted total least squares，WTLS）进行估计.采用模拟变换数据验证了本文方法的有效性，与LS和TLS法比较，该方法明显提高了尺度参数估计精度，外围坐标变换精度明显得到提高.

1 三维坐标变换的两步解法

当旋转角是微小量时，Bursa-Wolf模型可以通过下式来描述：

式中：bt=［Xti，Yti，Zti］T表示目标系统中第i个公共点；bo=［Xoi，Yoi，Zoi］T表示原系统中第i个公共点；ΔC=［ΔX，ΔY，ΔZ］T表示平移参数；R表示旋转矩阵；δμ表示尺度参数；εX，εY，εZ表示旋转参数.由于建立小区域控制网时，公共点不可能均匀地分布在全球的不同区域，直接采用上述Bursa-Wolf模型进行参数估计时旋转参数和平移参数之间存在非常强的相关性［2］，容易造成解算过程出现病态问题，参数估计结果不稳定，极小的观测误差都会引起极大的估计误差.这说明观测数据和模型之间出现了矛盾，模型不完全适合此时的数据处理需求.如果将原始Bursa-Wolf模型进行改造，将平移参数和旋转参数分开估计即可解决该矛盾，从而消除估计过程中参数之间的相关性.

平移参数可以在旋转参数和尺度参数得到估计后计算而得［15］.为了能够先估计旋转参数，需要先将平移参数从模型中消除.消除平移参数后的Bursa-Wolf模型可以表达为［7］

式中：Y=PmΛY；A=PmΛA；Pm是m个公共点之间的权矩阵；Λ=Im-（1TmP2m1m）-1（1m1TmP2m）是幂等矩阵（idempotent matrix）；1m表示元素值全等于1，大小为m×1的列向量.

在一次确定的变换过程中，如果尺度参数不变，并且不考虑控制点各坐标分量之间的相关性，TLS法和LS法将获得相同的旋转参数估计结果［7］.尽管小旋转角的Bursa-Wolf模型是一近似模型，但在理论上其仍应该满足正交变换条件，因此该结论在此也成立.这些结论说明Bursa-Wolf模型的各参数是可以分开进行估计的，证明了两步法进行参数估计的合理性.旋转参数可以通过对如下模型采用LS估计得到：

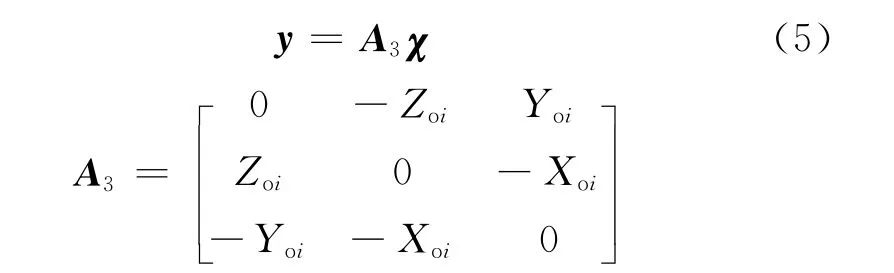
式中：y=［XtiYtiZti］T=vec（Y）；A3是由A中元素重组而成；χ=［εXεYεZ］T表示旋转参数矢量.其实该处也可以用TLS进行参数估计，但考虑到TLS和LS估计旋转参数具有等价性，为了简化计算采用了LS估计.

很显然，如果直接采用LS法估计模型（1）的参数，通过法方程系数矩阵可以计算参数之间的验后方差-协方差矩阵.通过前面的分析知道，平移参数和旋转参数的协方差值此时不全等于零，存在相关性.这种相关性可以理解为是由平差模型病态引起的.采用LS对模型（5）进行估计时可以得到旋转参数之间的方差-协方差矩阵.采用TLS对模型（6）进行参数估计时可以得到尺度参数和平移参数之间的方差-协方差矩阵.由于此时旋转参数被看作是常数，因此不存在旋转参数和尺度参数与平移参数之间的协方差值.这说明计算过程消除了旋转参数与平移参数的相关性，避免了解算ITLS问题.

在求得旋转参数以后，将旋转参数回代到原始Bursa-Wolf模型（1）中，可以得到只包含尺度参数和平移参数的新模型，即

式中：坐标矢量y中同时包含有目标系统和原系统的坐标，根据误差传播定律可以得到其方差-协方差矩阵，即

式中⊗表示矩阵的克罗内克积.

系数矩阵A4不仅含有误差而且具有较强的结构特性，这种结构性表现为矩阵中不同位置出现了相同元素值，而且包含有大量的常数元素.WTLS法可以同时处理系数矩阵的误差和结构问题.在已知尺度参数和平移参数的近似值情况下，参数ξ的估计公式可以表达为［16］

参数估计过程是一个无限逼近的过程，需要不断迭代计算直到收敛为止.

2 两步法计算变换参数的流程

根据前面的讨论，两步法计算局部区域三维坐标变换参数的流程可以概括如下：① 根据给定公共点坐标，根据公式（3）和（4）分别计算Y和A；② 计算幂等矩阵Λ=Im-（1TmP2m1m）-1（1m1TmP2m）；③ 计算Y=PmΛY和A=PmΛA；④采用LS法计算旋转参数χ＾=（AT3A3）-1AT3y；⑤ 根据参数的估计值重组矩阵Ξ；⑥ 根据公式（7）计算新的协方差矩阵Qy；⑦ 在模型（6）基础上采用LS法估计参数ξ（0）；⑧ 令υ=0，用公式（8）计算参数的第一次迭代值ξ（1）；⑨ 采用公式（10）计算新的权矩阵Q-1Y；⑩ 将⑨的结果代入到公式（9）中计算去正则因子υ；○11 将⑩得到的去正则因子带入到公式（8）中计算新的参数估计值；○12 与前一次估计的尺度参数和平移参数进行比较，如果两次之差的2阶范数≤10-10，则停止迭代.否则重复⑨到○11，直到满足上述条件为止；○13 输出参数估计值.

3 模拟实验与分析

3.1 实验数据模拟

原系统坐标模拟：在 WGS-84椭球上，从北纬20°，东经110°度开始，分别向北和向东每间隔2km取1个点，总共121个点，如图1所示.将2km对应的距离转换成角度值，采用WGS-84椭球参数计算每个点的三维直角坐标值.选择靠内部的8个点作为控制点（公共点），其余的点作为待转换点，有1个待转换点在控制点内部，其余点在控制点外围，如图1所示.

目标系统坐标模拟：将前面得到的三维直角坐标采用如公式（1）描述的Bursa-Wolf模型转换到目标系统中.根据实际经验将转换参数设计为：εX=0.000 4rad，εY=0.000 5rad，εZ=0.000 6rad，δμ=2×10-10，ΔX=-100m，ΔY=200m，ΔZ=-300 m.

观测值模拟：对公共点在两套系统中的3个坐标分量和原系统中待转换点的3个坐标分量都附加上期望为0，中误差为0.06m的随机误差.

3.2 实验对比与分析

根据上节模拟的观测值，采用LS法、TLS法和本文给出的两步法估计七参数.得到估计参数后将原系统中的非公共点坐标利用估计的参数和Bursa-Wolf模型转换到目标系统中.为了给出具有统计意义的参数估计结果，将3种方法每次获得的参数估计结果与真值相减求得绝对误差，然后将差值与真值相比求得相对误差，计算公式分别为

其中，θ代表7个参数中的任意一个.

3种方法都计算1 000次，按公式（11）和（12）计算绝对误差和相对误差，并将1 000次的平均值列于表1中.TLS法和LS法计算1 000次得到的验后方差分量估计结果制成图2.从表1可以看出，与LS和TLS相比较两步法主要提高了尺度参数和平移参数的估计精度，特别是尺度参数的精度.由于TLS法是一个去正则化的过程，在参数估计过程中模型病态较LS法更为严重，同时解TLS法需要迭代解算，因此当设置较高的收敛条件时TLS法可能出现不收敛.因此，本文在实验过程中设置了较大的收敛阈值，两次之差小于10-6即可.这可以解释为什么TLS法和LS法的参数估值差异非常小.

图1 实验点位分布Fig.1 Distribution of simulate points

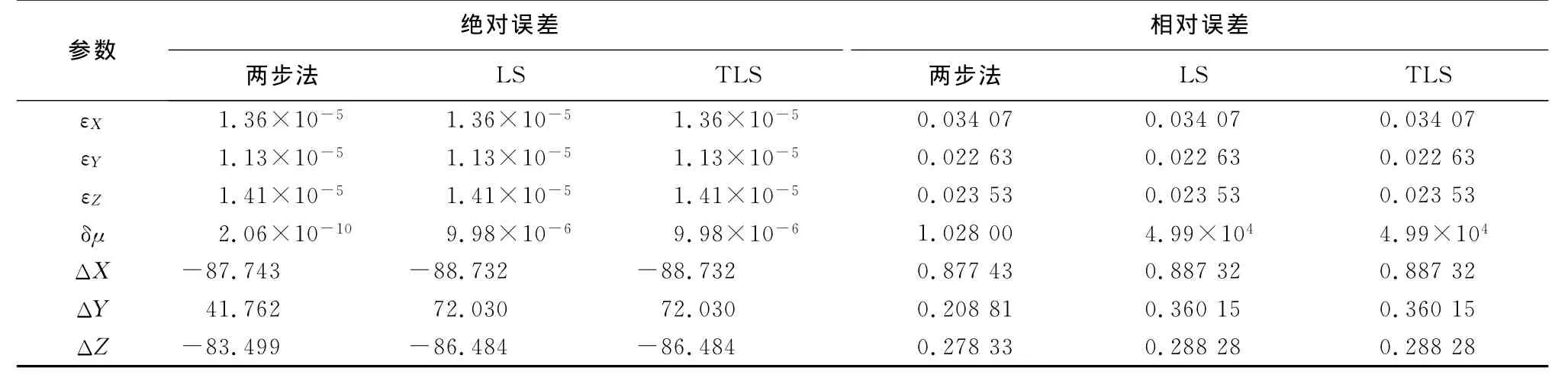
表1 不同方法参数估计结果比较Tab.1 Comparison of estimated parameters among two step，least squares and total least squares

图2 最小二乘法和整体最小二乘法方差分量估计结果比较Fig.2 Comparison of estimated variance component between LS and TLS

从图2可以明显发现TLS法获得的方差分量估计值更接近模拟先验值.由于本文没有给出验后方差分量计算公式，如果需要可以采用TLS的计算结果.TLS法采用文献［16］提供的公式计算，无偏计算公式可以参考文献［17-18］.LS法采用传统的计算方法.

为统计3种方法获得的变换参数对变换结果的影响，需要对变换点的点位误差进行统计分析.变换点三坐标分量的平均标准差可以按下式计算：

则可以得到变换点的点位中误差计算公式为

式中k表示转换点的总数.当取k=113时，即将图1中所有五角星标记的点放在一起统计.根据两步法，LS法和TLS法估计的参数将这些点从原系统变换到目标系统中，采用式（16）计算中误差，模拟1 000次.图3表达了这3种方法的模拟结果.图4描述了两步解得到的中误差与LS法和TLS法的差值.这两幅图说明，两步法的变换结果在统计上优于LS法和TLS法.将图1中的模拟点从内到外分成一个内部点和外面5圈，第1圈即用于求取变换参数的公共点（共8个），接着分别是第2圈到第5圈，圈与圈之间间隔2km.此时k分别等于16，24，32和40.除公共点外，其余每圈都按公式（16）进行中误差计算，模拟1 000次，将平均值绘制成如图5所示的柱状图.从图中可以看出，对于内部点，3种方法的变换精度是一致的；当随着变换点离控制点越来越远，尽管整体变换精度在下降，但是两步解法的精度始终比其他2种方法高，距离越远，精度提高得越明显.

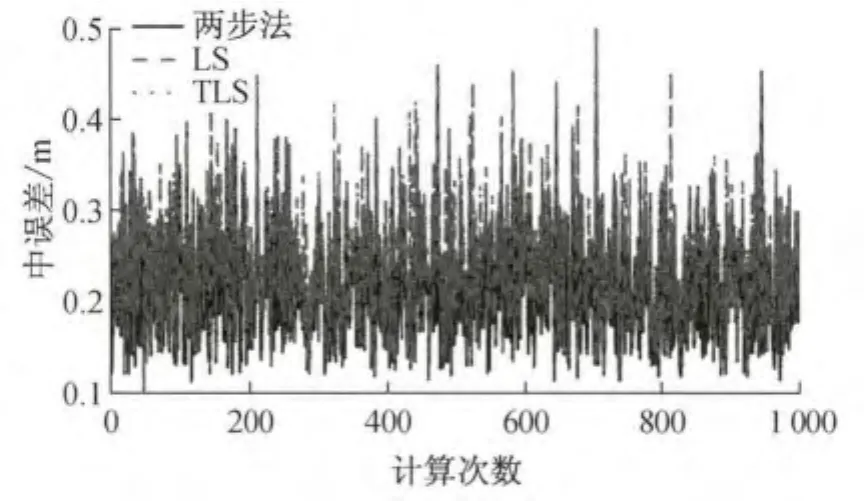
图3 两步解、最小二乘解和整体最小二乘解转换的内、外围坐标的中误差Fig.3 Mean square errors of inside and outside transformed coordinates with two step，LS and TLS accordingly

图4 两步解、最小二乘解和整体最小二乘解转换的内、外围坐标的中误差之差Fig.4 Difference of mean square errors of inside and outside transformed coordinates between two step，LS and TLS

4 结论

（1）虽然用整体最小二乘法求取的小区域三维坐标变换参数同最小二乘法差异较小，但其能够获得更为准确的验后方差估计结果.

（2）两步解法相对于LS法和TLS法，主要提高了尺度参数和平移参数的估计精度，特别是尺度参数.

图5 两步解、最小二乘解和整体最小二乘解转换的内部点和外围不同圈层坐标的平均中误差Fig.5 Average of mean square errors of transformed coordinates between two step， LS and TLS located at different circles from inside to outside accordingly

（3）两步解法同文献［2］所描述的方法一样，都能够提高外围点的变换精度，但是两步解法考虑了原系统坐标的误差.

［1］ 李微晓，沈云中，李博峰.顾及2套坐标误差的三维坐标变换方法［J］.同济大学学报：自然科学版，2011，39（8）：1243.LI Weixiao，SHEN Yunzhong，LI Bofeng.Three-dimensional coordinate transformation with consideration of coordinate errors in two coordinate systems［J］.Journal of Tongji University：Natural Science，2011，39（8）：1243.

［2］ 沈云中，胡雷鸣，李博峰.Bursa模型用于局部区域坐标变换的病态问题及其解法［J］.测绘学报，2006，35（2）：95.SHEN Yunzhong，HU Leiming，LI Bofeng.Ill-posed problem in determination of coordinate transformation parameters with small area's data based on bursa model ［J］.Acta Geodaetica et Cartographica Sinica，2006，35（2）：95.

［3］ 陈义，沈云中，刘大杰.适用于大旋转角的三维基准转换的一种简便模型［J］.武汉大学学报：信息科学版，2004，29（12）：1101.CHEN Yi，SHEN Yunzhong，LIU Dajie.A simplified model of three dimensional-datum transformation adapted to big rotation angle［J］.Journal of Wuhan University ：Geomatics and Information Science，2004，29（12）：1101.

［4］ 陆珏，陈义，郑波.总体最小二乘方法在三维坐标转换中的应用［J］.大地测量与地球动力学，2008，28（5）：77.LU Jue，CHEN Yi，ZHENG Bo.Applying total least squares to three-dimensionaldatum transformation［J］.Journal of Geodesy and Geodynamics，2008，28（5）：77.

［5］ 陆珏，陈义，郑波.加权总体最小二乘方法在ITRF转换中的应用［J］.大地测量与地球动力学，2011，31（4）：84.LU Jue，CHEN Yi，ZHENG Bo.Application of weighted total least squares in ITRF transformation［J］.Journal of Geodesy and Geodynamics，2011，31（4）：84.

［6］ 袁庆，楼立志，陈玮娴.加权总体最小二乘在三维基准转换中的应用［J］.测绘学报，2011，40（增1）：115.YUAN Qing，LOU Lizhi，CHEN Weixian.The application of the weighted total least-squares on three dimensional-datum transformation［J］.Acta Geodaetica et Cartographica Sinica，2011，40（Suppl.1）：115.

［7］ Felus A，Burtch R C.On symmetrical three-dimensional datum conversions［J］.GPS Solution，2009，13（1）：65.

［8］ Mahaoub V.On weighted total least-squares for geodetic transformations［J］.Journal of Geodesy，2011，86（5）：1.

［9］ 李博峰，沈云中，李微晓.无缝三维基准转换模型［J］.中国科学：地球科学，2012，42（7）：1047.LI Bofeng，SHEN Yunzhong，LI Weixiao.The seamless model for three-dimensional datum transformation ［J］.Scientia Sinica Terrae，2012，42（7）：1047.

［10］ LI Bofeng，SHEN Yunzhong， LOU Lizhi.Noniterative datum transformation revisited with two-dimensional affine model as a case study［J］.Journal of Surveying Engineering，2013，139（4）：166.

［11］ LI Bofeng，SHEN Yunzhong，ZHANG Xinfu ，etal.Seamless multivariate affine error-in-variables transformation and its application to map rectification［J］.International Journal of Geographical Information Science，2013，27（8）：1572.

［12］ 葛旭明，伍吉仓.病态总体最小二乘问题的广义正则化［J］.测绘学报，2012，41（3）：372.GE Xuming，WU Jicang.Generalized regularization to illposed total least squares problem［J］.Acta Geodaetica et Cartographica Sinica，2012，41（3）：372.

［13］ 葛旭明，伍吉仓.误差限的病态总体最小二乘解算［J］.测绘学报，2013，42（2）：196.GE Xuming，WU Jicang.A regularization method to ill-posed total leastsquares with error limits ［J］.Acta Geodaetica et Cartographica Sinica，2013，42（2）：196.

［14］ 袁振超，沈云中，周泽波.病态总体最小二乘模型的正则化算法［J］.大地测量与地球动力学，2009，29（2）：131.YUAN Zhenchao， SHEN Yunzhong， ZHOU Zebo.Regularized total least-squares solution to ill-posed error-invariable model［J］.Journal of Geodesy and Geodynamics，2009，29（2）：131.

［15］ SHEN Yunzhong，CHEN Yi，ZHENG Dehua.A quaternionbased geodetic datum transformation algorithm［J］.Journal of Geodesy，2006，80（5）：233.

［16］ Schaffrin B， Wieser A.On Weighted total least-squares adjustment for linear regression［J］.Journal of Geodesy，2008，82（7）：415.

［17］ SHEN Yunzhong，LI Bofeng，CHEN Yi.An iterative solution of weighted total least-squares adjustment［J］.Journal of Geodesy，2011，85（4）：229.

［18］XU Peiliang，LIU Jinnan，SHI Chuang.Total least squares adjustment in partial errors-in-variables models：Algorithm and statistical analysis［J］.Journal of Geodesy，2012，86（8）：661.