一种改进的最大一致性点云几何基元拟合算法
2015-04-16刘修国王红平
刘修国,杨 准,王红平,梁 栋
(中国地质大学(武汉)信息工程学院,湖北 武汉430074)
平面、二次曲面(球、圆柱、圆锥)等基本几何基元的高精度拟合是点云数据处理的基础工作.高精度几何基元拟合获取几何基元可靠参数,可实现标靶高精度定位,完成基于标靶[1]或基于几何基元[2]的多测站配准;也有助于点云分割[3-5]中过分割、欠分割问题的解决,并有效支撑基于点云数据的表面建模[6-7].
近年来,几何基元的高精度拟合仍是点云数据处理的研究热点之一.文献[8-9]采用了基于特征值最小二乘的拟合方法,用于解决含有粗差的点云数据平面基元高精度拟合.文献[10-11]采用整体最小二乘方法拟合几何基元,该方法顾及点云数据在X,Y,Z3个方向存在的误差,拟合精度有所提高.文献[12]提出迭代平方距离函数最小化的曲面拟合方法,用平方距离度量点集与曲面基元的几何距离,用于拟合曲面基元.对于预先剔除粗差点后的点云数据,文献[10-12]的拟合方法能较高精度地拟合出平面或简单曲面几何基元.目前应用广泛且较成熟的是 随 机 抽 样 一 致 (random sample consensus,RANSAC)几何基元拟合算法[3-5,13];该算法支持对平面、二次曲面等多种几何基元的拟合,能在含有一定粗差的点云中可靠地拟合出几何基元.但RANSAC算法不能自适应地设定距离阈值以区分粗差点与非粗差点:阈值过大则不能完全剔除粗差,造成拟合精度不高甚至拟合失败;阈值过小会剔除较多非粗差点,难以保证特定几何基元点集的完整性[14],降低拟合精度.为此,文献[14]提出了 MCMD(maximum consistency with minimum distance and robust Z-score)算法.该算法基于主成分分析(principal component analysis,PCA)[15]选取可靠平面初值,再采用稳健Z分数法一次性剔除粗差,有效避免了距离阈值设置以区分粗差、非粗差点的问题.但MCMD算法基于PCA的初值选取准则仅适于平面基元,不适于二次曲面基元;同时,在点云数据粗差统计分布未知的复杂场景中,稳健Z分数法难以一次性剔除全部粗差,限制了该算法的适用性.
1 MCMD平面基元拟合算法思想
在获取可靠的平面初值后,采用稳健Z分数方法来剔除粗差,设点集Q中任意点qi∈Q到初始平面的垂直距离为di,则该点的稳健Z分数Zr,j定义为
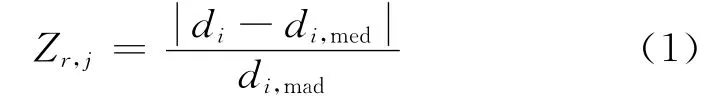
式中:di,med表示距离中位数;di,mad为距离的中位数中误差,其定义为
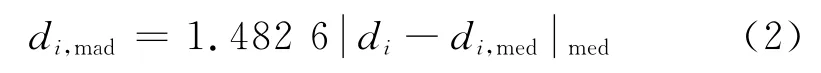
当Zr,j≥k0(2.0≤k0≤2.5)时,可认为qi点是粗差点[16].剔除掉点集Q中所有Zr≥k0的粗差点后,剩余点认为是属于同一平面基元的点,对其进行拟合获取最终的平面基元参数.
2 改进MCMD几何基元拟合算法
本文算法首先构建点子集的候选集合.设采用随机抽样思想从点集Q中产生的候选集合中有T个点子集,设点集Q中某一个点为非粗差点的概率为ε,确定待拟合基元形状参数的最少点个数为N0,循环T次获取的T个点子集样本中至少有一个样本不含粗差的概率为Pr,则有1-Pr=(1-εN0)T,即
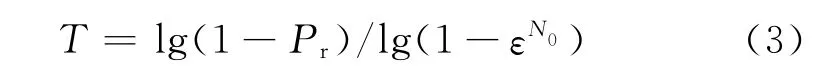
采用距离和最小初值选取准则从点子集的候选集合中选取最佳点子集,可靠的模型初值为最佳点子集对应的拟合几何基元参数.
改进的算法流程见图1.
2.1 距离和最小的初值选取准则
距离和最小的初值选取准则,即点子集到拟合模型的距离和越小则点共表面程度越大.以距离和最小作为最优模型初值的选取准则,扩展MCMD算法使之适用二次曲面基元的拟合.
距离和是指选取的点子集中每个点到拟合模型距离的总和.对平面而言,距离和是点到平面模型d=ax+by+cz的垂直距离和,其计算公式为
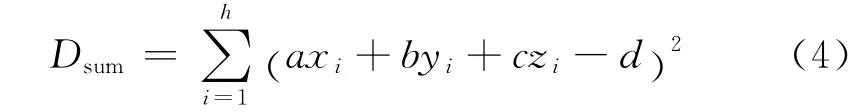
式中:Dsum表示距离和;a,b,c,d均为平面参数;h为点子集的数目.
对于二次曲面(球体、圆柱、圆锥)而言,距离和是指点子集中每个点到曲面的平方距离和.与垂直距离相比,平方距离能更加精确地表示点与拟合模型的几何距离[12,17].平方距离和的计算公式为
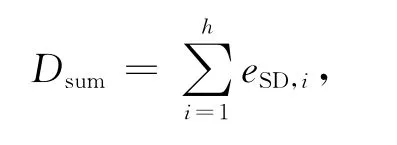
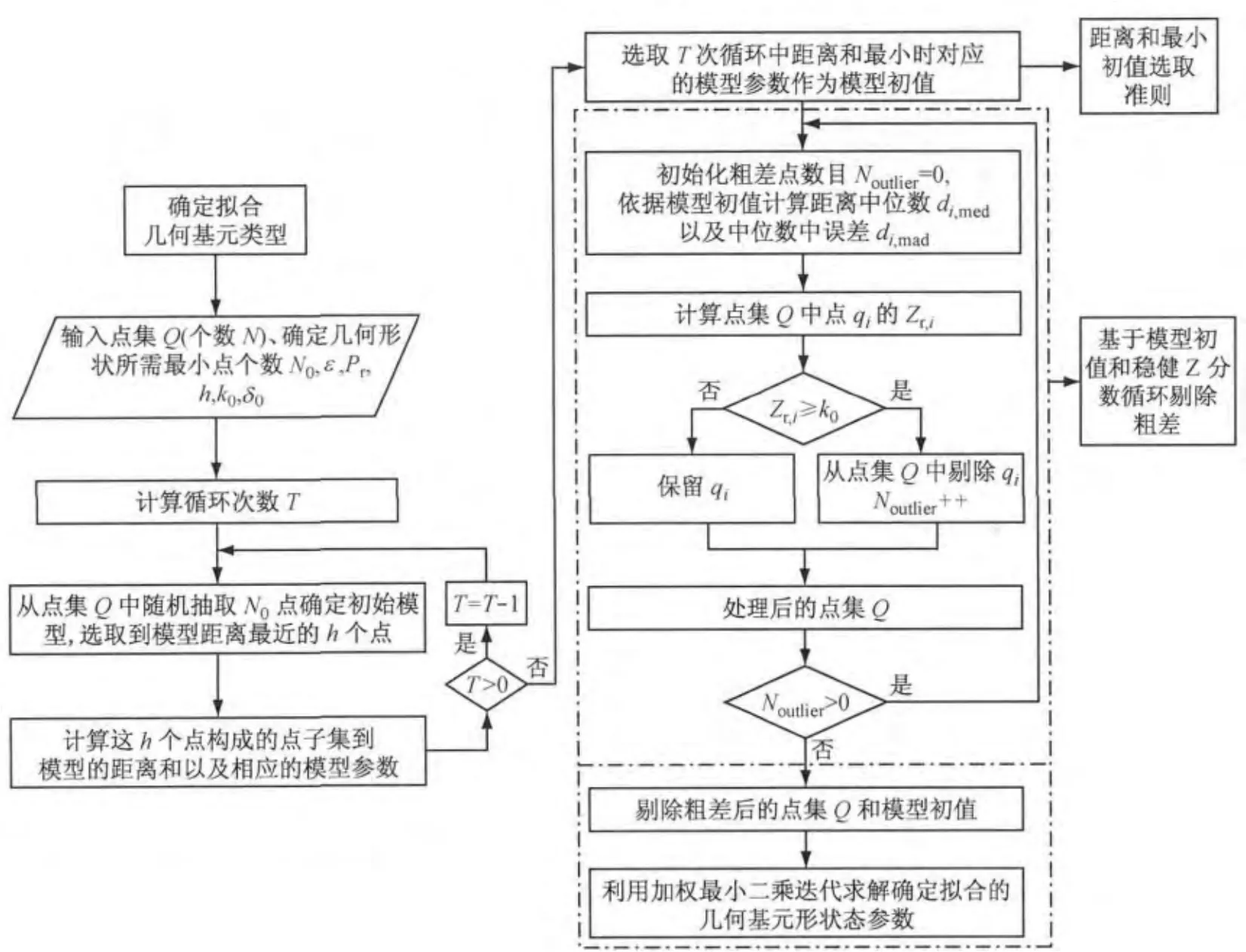
图1 改进的MCMD算法流程Fig.1 Flowchart of improved MCMD algorithm
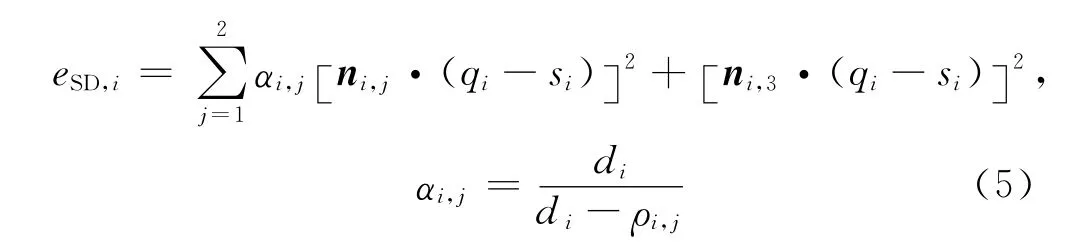
式中:对于三维表面S,eSD,i为第i个点到模型表面的平方距离;si代表S上与qi最近的点,si处的曲率半径为ρi,1和ρi,2;ni,1,ni,2为主曲率方向向量,ni,3为法向量;最短距离为.若曲率中心与点qi在表面S的两侧,则di<0;反之di>0,当0<di<ρi,j或者ρi,j为无穷大时,αi,j=0.
2.2 粗差剔除与模型参数求解
在复杂目标场景中,粗差点统计分布规律是未知的,此时粗差难以一次性剔除.本文算法采用稳健Z分数方法循环剔除粗差策略逐步剔除粗差,即每次循环依据距离和最小准则获取可靠初始模型,重新计算垂直距离中位数di,med、中位数中误差di.mad,并计算点集Q中每个点的Zr值;将Zr≥k0的点从点集中剔除,当点集中所有点的Zr<k0时停止循环.
对剔除粗差后的点集采用加权最小二乘法迭代优化获取最终的几何基元形状参数.
对平面基元:d=ax+by+cz,待求参数为单位法向量n=(a,b,c),原点到平面的距离d.点集中任意点qi=(xi,yi,zi)到平面的有向距离为
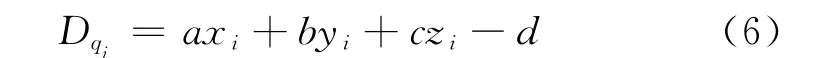
对球面基元:(xi-x0)2+(yi-y0)2+(zi-z0)2=r,待求参数为球中心o=(x0,y0,z0)、球半径r.则点集中任意点qi=(xi,yi,zi)到球面的有向距离为
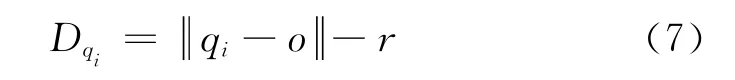
对圆柱基元:(xi-x0)2+(yi-y0)2+(zi-z0)2-[nx(xi-x0)+ny(yi-y0)+nz(zi-z0)]2=r2,待求参数为圆柱单位轴向n=(nx,ny,nz)、轴向上一点o=(x0,y0,z0)及圆柱半径r.则点集中任意点qi=(xi,yi,zi)到圆柱的有向距离为
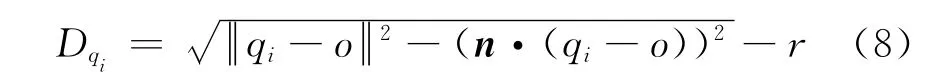
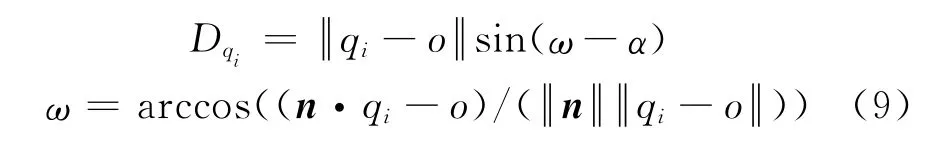
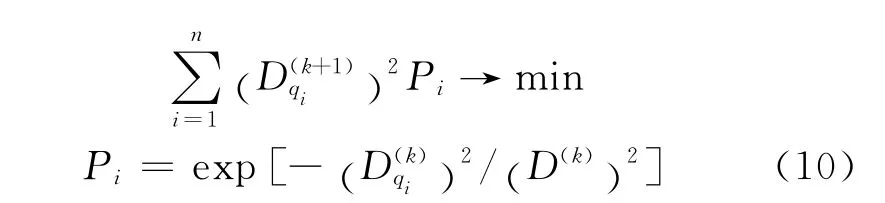
式中:Pi为权函数;D(k)i为第k次迭代点到几何基元的有向距离;D(k)为距离的范围.
设置迭代阈值δ0,当两次迭代获取的对应参数差值小于δ0,停止迭代获取几何基元形状参数.
3 实验结果与分析
3.1 平面拟合实验
首先采用模拟数据评估算法的粗差识别能力及拟合精度.模拟的平面方程为2=x+y+z,坐标(x,y)在区间[0,1]上服从均匀分布,坐标z的值由模拟的平面方程计算得到.在模拟点坐标(x,y,z)均加上误差ν~N(0,0.002)形成非粗差点.模拟两种粗差点分布(图2):①粗差点分布在模型一侧(分布A),即对模拟点坐标(x,y,z)加上均值分别为(0.8,0.9,1.0)、方差均为0.5的高斯分布;②粗差点分布在模型两侧(分布B),即一半粗差点与分布A相同,另一半粗差点则是对模拟点坐标(x,y,z)加上均值分别为(-0.8,-0.9,-1.0)、方差均为0.5的高斯分布.
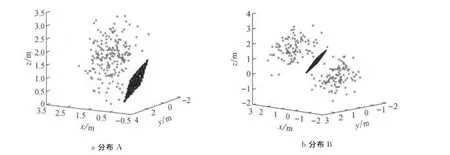
图2 两种粗差分布对应的模拟数据(粗差比率为20%)Fig.2 Simulated point cloud corresponding to distribution of two kinds of outliers(outlier rate is 20%)
对于两种粗差分布,在不同粗差比率(10%,20%,30%,40%,50%)下分别模拟产生1 000组数据集,每组数据集中包含1 000个点.利用本文算法、MCMD和RANSAC算法对模拟数据进行平面基元拟合.针对RANSAC难以设定距离阈值,本文通过设置不同距离阈值进行RANSAC算法实验,从中选取最优结果作为对比;本模拟数据中RANSAC算法距离阈值设为3mm.
采用正确识别比率(correct identificaiton rate,CIR)、错误识别比率(swamping rate,SR)两个指标[14]来评估拟合算法能否正确区分粗差点、非粗差点.拟合精度采用拟合平面与真实平面法向量夹角θ以及坐标原点到拟合平面距离与真实距离值间的差值ΔD评估.CIR指标为识别的粗差点中真实粗差点个数与总的粗差点个数之比,SR指标为识别的粗差点中非粗差点的个数与总的非粗差点个数之比.3种算法的CIR与SR均值统计见表1,拟合精度指标如图3与图4所示.
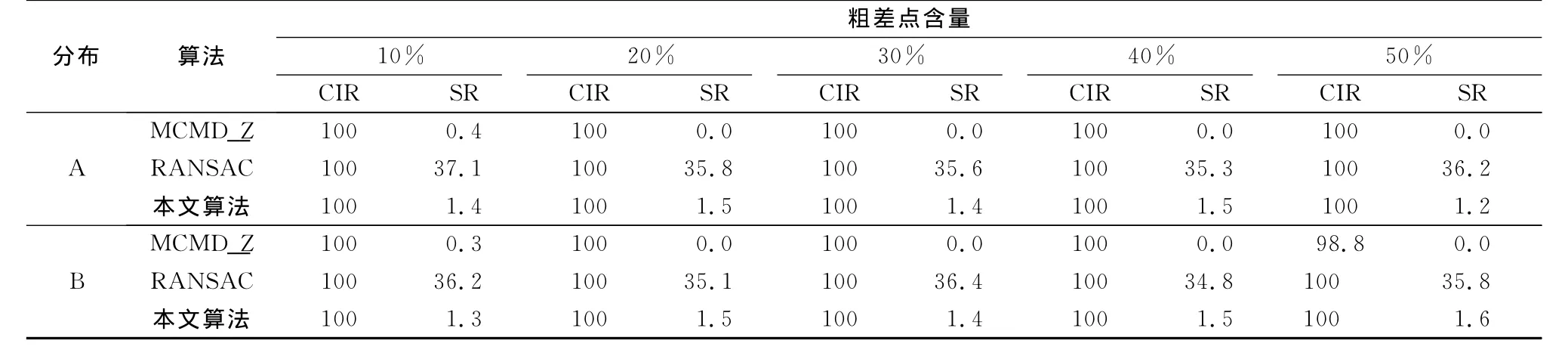
表1 平面拟合的CIR与SR指标Tab.1 CIR and SR of plane fitting
从表1可以看出,RANSAC算法的CIR指标为100%,即能剔除全部粗差.但该算法SR指标均大于30%,破坏了平面基元点的完整性,也造成平面拟合精度较低.MCMD算法SR指标均小于0.4%,该算法的平面点集完整性与平面拟合精度较
RANSAC显著提高,但是其在粗差比率为50%的分布B模拟数据时CIR为98.8%,不能剔除所有粗差,这与第1节分析得出的MCMD算法局限②相吻合.本文算法CIR指标全部为100%,能够完全剔除粗差.而SR指标均低于1.6%,略高于MCMD算法.这是因为本文算法采用了循环稳健Z分数剔除粗差策略,使得在复杂场景中能完全剔除粗差且尽可能保证属于同一几何基元点集的完整性.
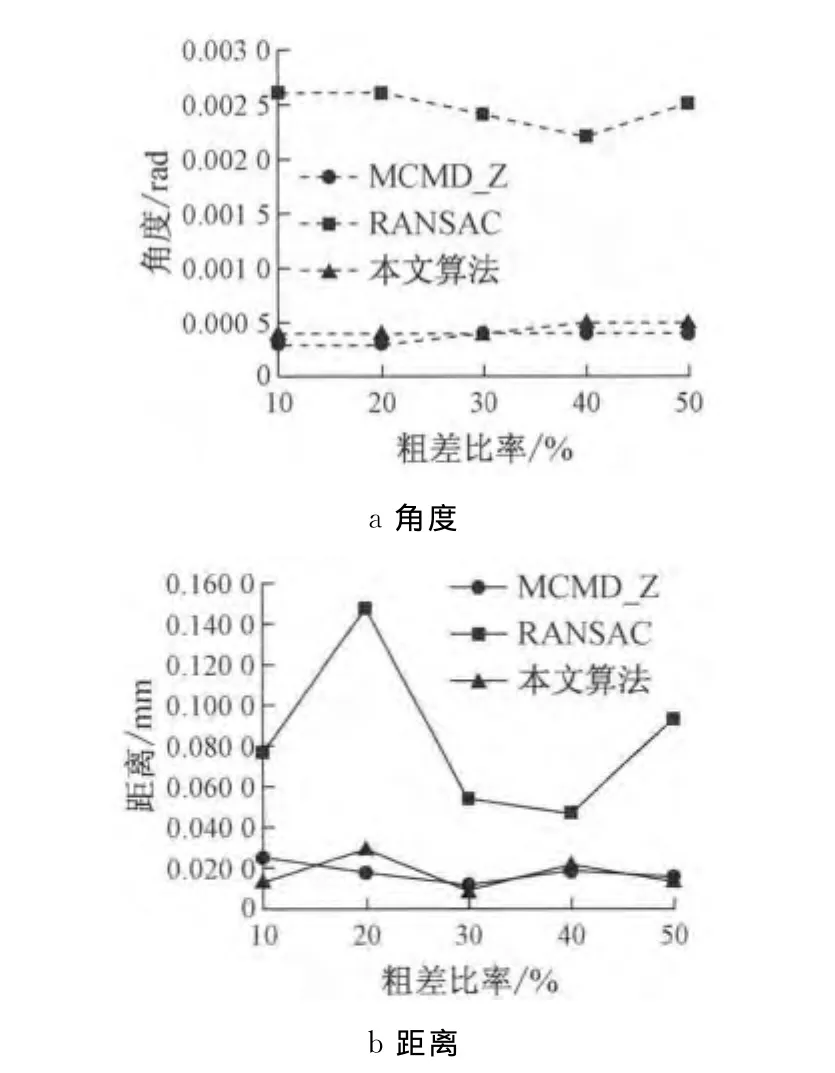
图3 粗差分布A对应的平面拟合精度Fig.3 Plane fitting accuracy corresponding to distribution of outlier A
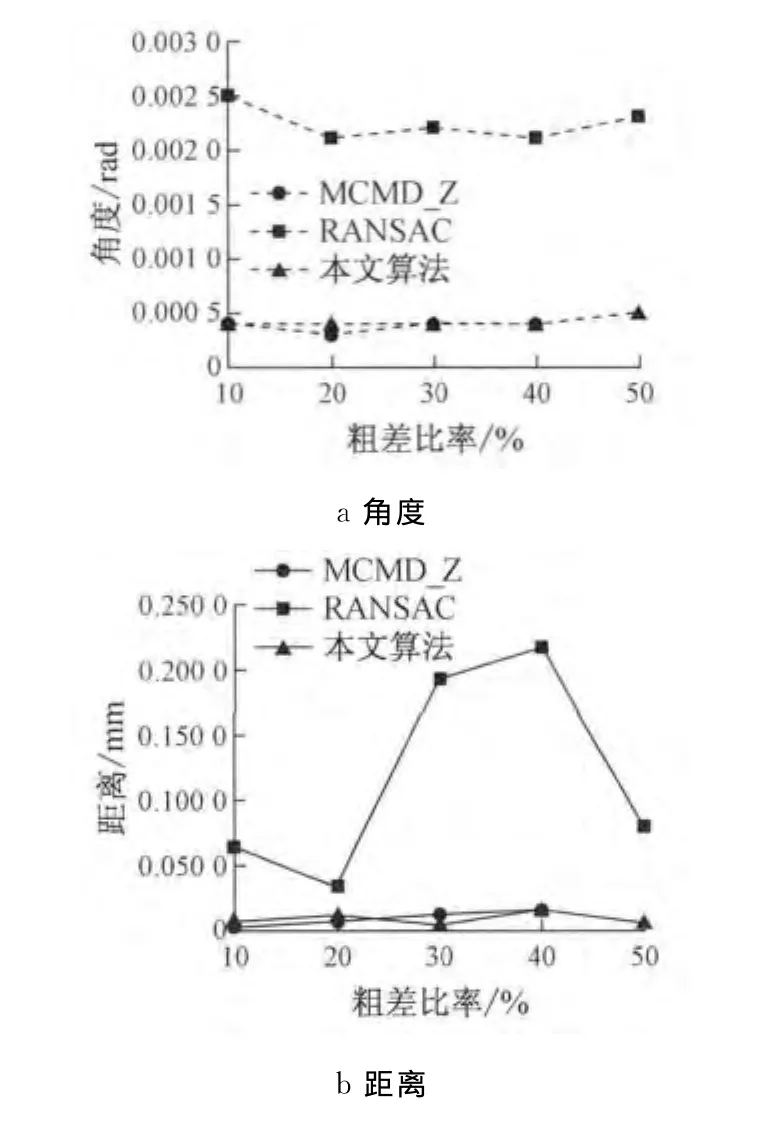
图4 粗差分布B对应的平面拟合精度Fig.4 Plane fitting accuracy corresponding to distribution of outlier B
从图3与图4可以看出,3种算法中RANSAC算法拟合精度最低,而本文算法与MCMD算法拟合精度相当.值得注意的是,对粗差比率为50%的分布B模拟数据,MCMD算法不能剔除全部粗差,使得拟合失效.
采用真实数据验证本文算法对目标多样、存在遮挡、点密度变化显著的复杂场景的粗差剔除能力.如图5所示(第1行为正视图,第2行为顶视图),点云数据中主墙平面为待拟合平面;场景中存在遮挡主墙平面的电缆线(图5标号1)、砖块(图5标号2)、树木(图5标号3)等不同目标;存在位于树叶之后点密度稀疏的墙面区域(图5标号4).对此复杂场景,分别采用MCMD,RANSAC与本文算法进行粗差剔除,其中RANSAC算法距离阈值设置为3 mm.各算法保留的主墙平面基元点集结果见图5,法向夹角θ与距离偏差ΔD统计结果见表2.

表2 墙平面拟合结果Tab.2 Results of facade plane fitting
3.2 球面拟合实验
采用地面三维激光扫描仪获取的标靶球进行拟合并评估其精度.将获取的数据场景中5个标靶球(图6)分割出来,对5个标靶分别进行拟合,其中RANSAC算法距离阈值设为3.5mm,相关的拟合结果见表3.其中识别率为算法自动识别的球面点与人工识别的球面点的比值;球心误差为算法自动拟合球心与人工识别的点拟合得到的球心欧氏距离.
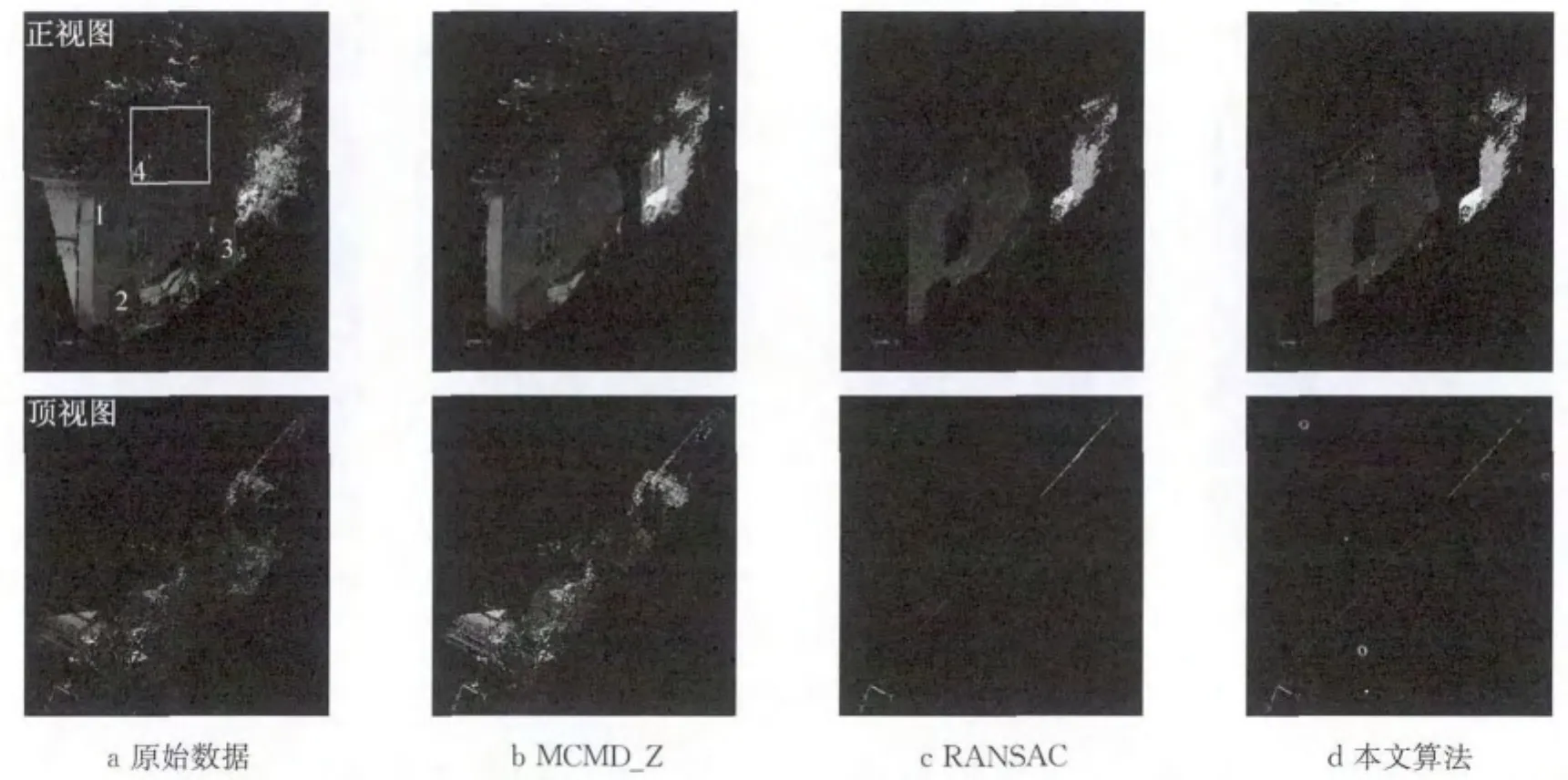
图5 复杂场景下剔除粗差后的墙平面Fig.5 Plane data after romving outliers in complex scene

图6 真实场景标靶球数据Fig.6 Sphere target data from scanning scene
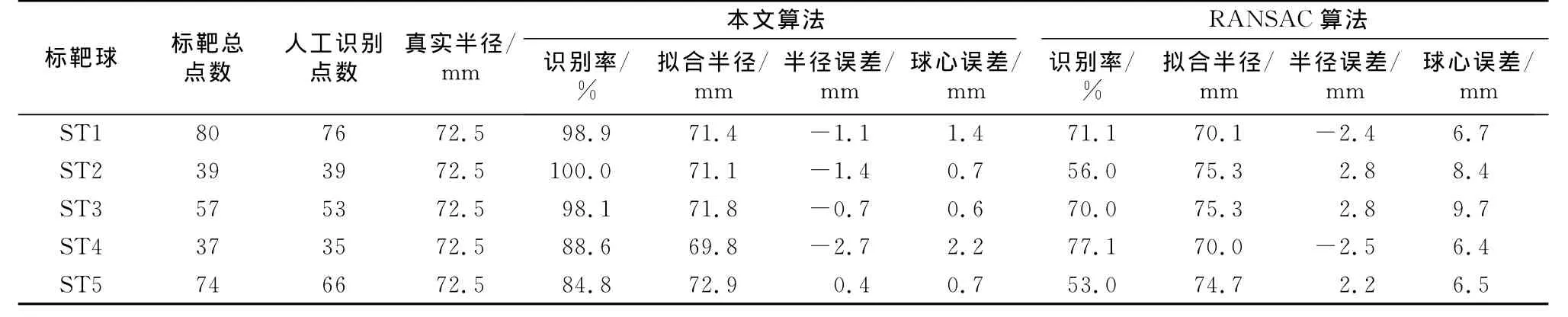
表3 标靶球拟合结果Tab.3 Results of sphere target fitting
从拟合结果来看,RANSAC算法过多地剔除了非粗差点,拟合精度不高;而本文算法拟合结果较好,即使在获取的标靶球点数目较少的情况下,本文算法的拟合结果也与人工识别的结果相当.
3.3 圆柱与圆锥拟合实验
对地面三维激光扫描仪获取的圆柱进行拟合并评估拟合精度.圆柱基元的参数包括轴线上的一个点、轴线方向及其轴半径.采用RANSAC算法与本文算法对圆柱点云进行拟合,其中RANSAC算法距离阈值设为4mm,相应的拟合结果如图7与表4所示.其中识别率为算法自动识别的圆柱点与人工识别的圆柱点的比值;轴线距离为算法自动拟合轴线与人工拟合轴线间的最小距离;轴线误差为算法自动拟合轴线与人工拟合轴线间夹角;半径误差为算法自动拟合半径与人工拟合半径差的绝对值.

表4 圆柱拟合结果Tab.4 Results of cylinder fitting
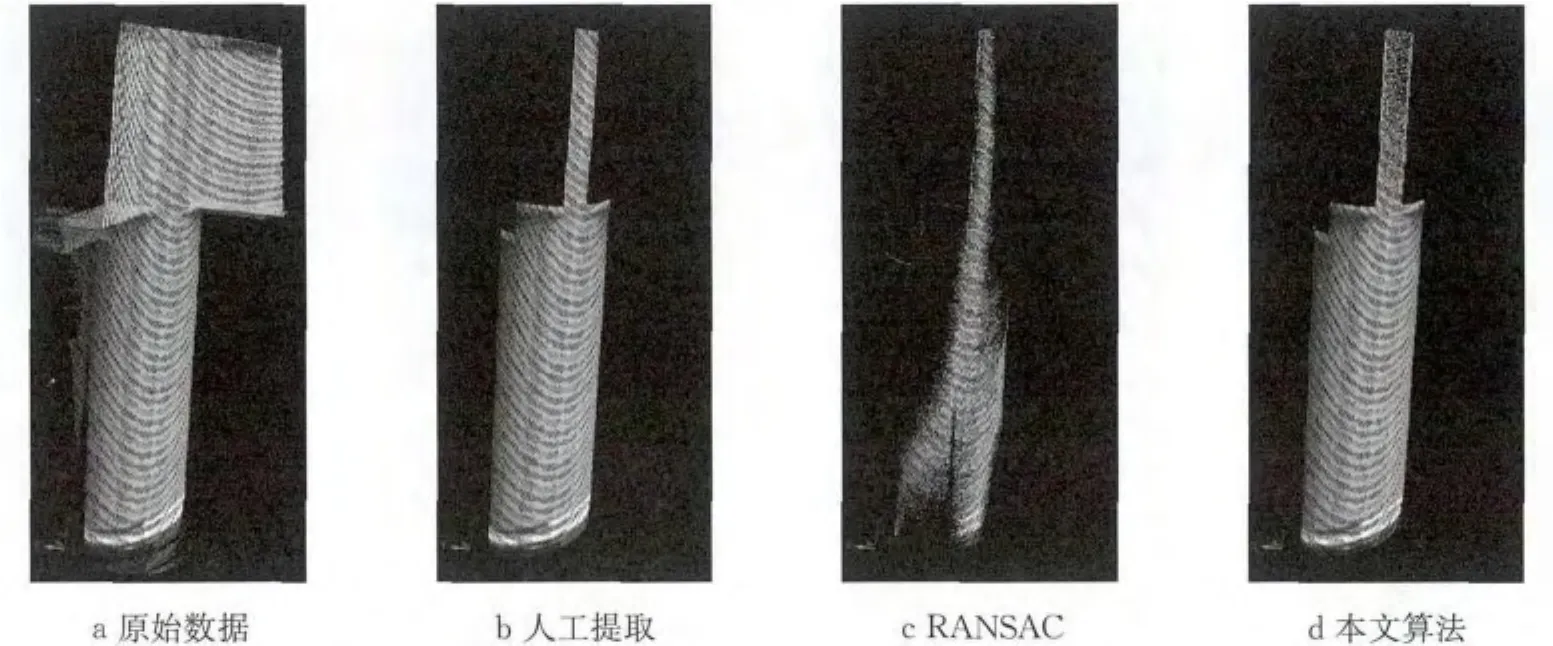
图7 粗差剔除后属同一圆柱基元的点集Fig.7 Cylinder data after removing outliers
对圆锥拟合实验则采用顶点为(0,0,0)、轴向为(0,0,1.0)、顶角为90°的圆锥模拟数据.圆锥模拟数据生成方法与平面模拟数据生成类似,模拟验证数据粗差比率为30%.拟合结果见图8与表5,其中RANSAC算法距离阈值设为2.5mm.顶点误差为算法拟合顶点与模拟模型顶点的欧式距离,顶角误差为算法拟合顶角与模拟模型顶角差值.

表5 圆锥拟合结果Tab.5 Results of cone fitting
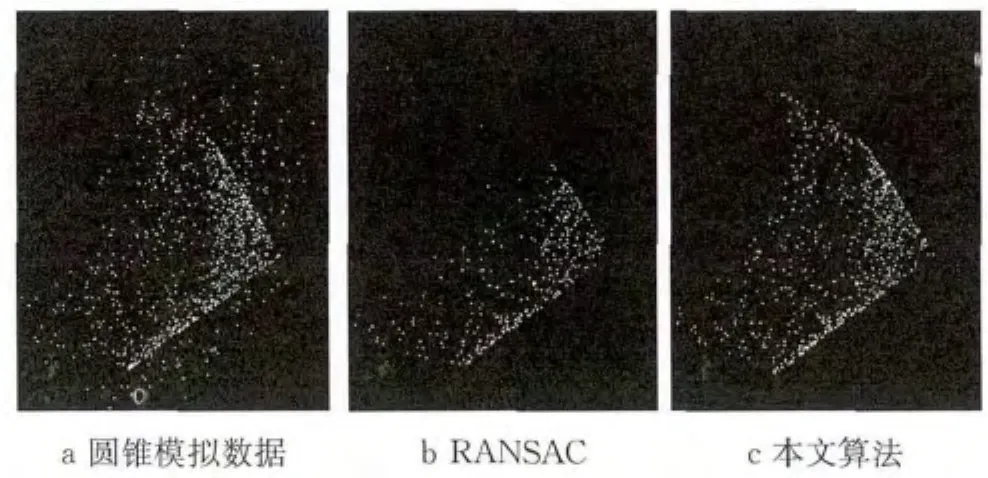
图8 粗差剔除后属同一圆锥基元的点集Fig.8 Cone data after removing outliers
从圆柱、圆锥基元拟合结果可以看出,本文算法同样适用,且能有效剔除粗差,保证较高的识别率,获得高精度的基元参数,各项拟合误差均比RANSAC算法拟合误差小.
4 结论
[1] 陈西江,花向红,杨荣华,等.分带K-均值聚类的平面标靶定位[J].武汉大学学报:信息科学版,2013,28(2):167.CHEN Xijiang,HUA Xianghong,YANG Ronghua,etal.Planar target location based on the zoning K-means clustering[J].Geomatics and Information Science of Wuhan University,2013,28(2):167.
[2] Theiler P W,Schindler K.Automatic registration of terrestrial laser scanner point clouds using natural planar surfaces[C]∥XXII ISPRS Congress,Technical Commission III.Melbourne:Copernicus Publications,2012:173-178.
[3] PU Shi,Vosselman G.Automatic extraction of building features from terrestrial laser scanning[J].International Archives of Photogrammetry,Remote Sensing and Spatial Information Sciences,2006,36(5):25.
[4] Schnabel R,Wahl R,Klein R.Efficient RANSAC for pointcloud shape detection[J].Computer Graphics Forum,2007,26(2):214.
[5] Zhang G,Karasev P,Brilakis I,etal.A sparsity-inducing optimization algorithm for the extraction of planar structures in noisy point-cloud data[C]∥ Proceedings of the 2012 ASCE International Conference on Computing in Civil Engineering.Clearwater Beach:ASCE Publications,2012:317-324.
[6] Kaucic R, Hartley R, Dano N.Plane-based projective reconstruction[C]∥ Eighth IEEE International Conference on Computer Vision.Vancouver:IEEE,2001:420-427.
[7] NAN Liangliang,Sharf A,ZHANG Hao,etal.Smart boxes for interactive urban reconstruction[J].ACM Transactions on Graphics,2010,29(4):1.
[8] 官云兰,程效军,施贵刚.一种稳健的点云数据平面拟合方法[J].同济大学学报:自然科学版,2008,36(7):981.GUAN Yunlan,CHENG Xiaojun,SHI Guigang.A robust method for fitting aplane to point clouds[J].Journal of Tongji University:Natural Science,2008,36(7):981.
[9] 王峰,丘广新,程效军.改进的鲁棒迭代最小二乘平面拟合算法[J].同济大学学报:自然科学版,2011,39(9):1350.WANG Feng,QIU Guangxin,CHENG Xiaojun.An improved robust method for iterating least-squares plane fitting[J].Journal of Tongji University:Natural Science,2011,39(9):1350.
[10] 鲁铁定,周世健,张立亭,等.基于整体最小二乘的地面激光扫描标靶球定位方法[J].大地测量与地球动力学,2009,29(4):102.LU Tieding,ZHOU Shijian,ZHANG Liting,etal.Sphere target fixing of point cloud data based on TLS[J].Journal of Geodesy and Geodynamics,2009,29(4):102.
[11] 官云兰,刘绍堂,周世健,等.基于整体最小二乘的稳健点云数据平面拟合[J].大地测量与地球动力学,2011,31(5):80.GUAN Yunlan,LIU Shaotang,ZHOU Shijian,etal.Robust plane fitting of point clouds based on TLS[J].Journal of Geodesy and Geodynamics,2011,31(5):80.
[12] WANG Jun,YU Zeyun.Quadratic curve and surface fitting via squared distance minimization[J].Computers &Graphics,2011,35(6):1035.
[13] Fischler M A,Bolles R C.Random sample consensus:A paradigm for model fitting with applications to image analysis and automated cartography[J].Communications of the ACM,1981,24(6):381.
[14] Nurunnabi A,West G,Belton D.Robust outlier detection and saliency features estimation in point cloud data[C]∥ 10th International Conference on Computer and Robot Vision(CRV).Regina:IEEE,2013:98-105.
[15] Hoppe H,DeRose T,Duchamp T,etal.Surface reconstruction from unorganized points[C]∥ Proceedings of the 19th Annual Conference on Computer Graphics and Interactive Techniques.New York:ACM Press,1992:71-78.
[16] 杨元喜.抗差估计理论及其应用[M].北京:八一出版社,1993.YANG Yuanxi.Robust estimation theory and its applications[M].Beijing:Bayi Publishing House,1993.
[17] Pottmann H,Hofer M.Geometry of the squared distance function to curves and surfaces[C]∥3rd International Workshop on Visualization and Mathematics.Berlin:Springer,2002:221-242.
