不同埋深下大直径盾构隧道横向刚度有效率

李晓军，黄伯麒，杨志豪，李新星

（1.同济大学 土木工程防灾国家重点实验室，上海200092；2.同济大学 岩土及地下工程教育部重点实验室，上海200092；3.同济大学 土木工程学院，上海200092；4.上海市隧道工程轨道交通设计研究院，上海200235）

盾构隧道衬砌结构纵缝接头的力学性能对于结构整体稳定性以及变形有着重要的影响，对于深埋及大直径盾构隧道这一影响则更为显著.目前对于盾构隧道衬砌结构横向计算理论的研究普遍考虑了纵缝接头对于整体刚度的影响，包括将管片与接头等效均匀化处理的修正惯用法，将两者分离考虑的梁-弹簧模型［1-2］、梁-接头不连续模型［3］以及壳-接头模型等［4-5］.基于均质等效刚度模型的修正惯用法因概念明确、计算简便，在设计中广泛采用，该方法关键之一在于计算参数的合理选择，横向刚度有效率η取值直接影响隧道衬砌结构设计是否安全和经济.用于确定刚度有效率η的方法主要包括经验取值、结构试验以及理论解析［6］.文献［6］列举了我国部分地铁盾构隧道刚度有效率的经验值，对于错缝拼装形式，一般在0.6～0.8之间，而日本隧道规范则建议取为0.8［7］，同时基于模型试验得到上海地铁盾构隧道通、错缝拼装情况下η分别为0.67及0.75；文献［8］基于狮子洋隧道和南京长江隧道的1∶1整环试验，得到前者在通、错缝拼装情况下η范围分别为0.5～0.7及0.6～0.8，后者在通、错缝拼装情况下η范围分别为0.50～0.65及0.6～0.7；文献［9］基于长江隧道1∶1整环试验结果，得到η范围为0.7～0.8，设计中取为0.8.此外，文献［10］采用梁-弹簧模型与修正惯用法，得到了η关于接头-管片弯曲刚度比的拟合公式.

上述研究大多针对地铁隧道，η的范围对于大直径盾构隧道的适用性有待验证.文献［8］的整环试验对于荷载形式进行了较大简化，在很大程度上影响了内力分布形式和管片接头变形程度，并影响了η取值；文献［10］所采用的接头模型形式过于简单，实际上同一管片环上不同位置处的接头刚度也并非定值.此外，上述研究普遍未考虑不同直径隧道所对应地基抗力系数的差异以及埋深对横向刚度有效率的影响.文献［11］研究表明，地基抗力系数与衬砌直径大致成反比关系；并且纵缝接头刚度受到应力水平的显著影响，不同的埋深和隧道直径对应着不同的应力水平.因此，对于深埋及大直径盾构隧道，以往用于确定横向刚度有效率η取值的经验参数可能不再适用.

本文以上海沿江通道工程为计算实例，给出一种可以考虑不同埋深条件影响的大直径盾构隧道横向刚度有效率计算方法及其取值建议.

1 计算模型的确定

1.1 工程概况

上海沿江通道工程盾构段隧道衬砌内径13.7 m，管片厚度65cm，环宽2m，混凝土等级为C60；衬砌环共分为10块，其中7块为标准块、2块为邻接块和1块为封顶快，如图1所示.封顶块的分块角度为18.519°，邻接块的分块角度为38.108°，B1和B7的分块角度为37.378°，B2和B6的分块角度为38.929°，B3和B5的分块角度为36.344°，B4的分块角度为39.963°，块间以2根M39螺栓相连；管片环采用错缝拼装；隧道覆土厚度范围为15～35m，土质主要为粉质黏土及砂质粉土.

图1 衬砌分块Fig.1 Lining blocks

1.2 横向有效刚度计算方法及计算模型

采用横向刚度有效率η作为反应衬砌结构横向力学性能的指标，其意义为考虑纵缝影响的衬砌环横向抗弯刚度与均质圆环横向抗弯刚度之比［12］，即

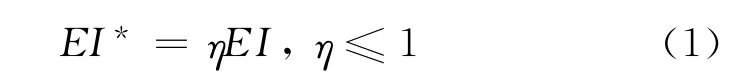
式中：EI为均质圆环横向抗弯刚度；EI＊为考虑接头不连续性影响、基于横向变形等效原则计算出的衬砌环横向抗弯刚度.η的确定方法为

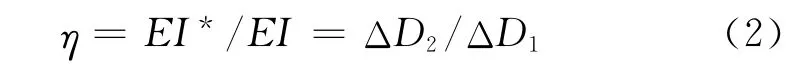
式中：ΔD2为考虑接头非连续性而计算得到的衬砌环横向变形；ΔD1为不考虑纵缝接头的均质圆环计算得到的衬砌环横向变形，如图2所示［12-13］.

图2 横向抗弯刚度有效率［12-13］Fig.2 Efficient ratio of bending rigidity［12-13］

由于地基与结构是一个受力整体，按照式（2）进行刚度折减没有考虑地基刚度补偿作用，因此需修正刚度有效率如下式：

式中，ΔD′2为均质圆环模型刚度按照 ΔD2／ΔD1进行折减计算得到的横向变形.

为考察错缝拼装方式对于横向刚度有效率的影响，计算模型分为单环模型和错缝双环模型，并且不考虑环间剪切错动变形.有限元计算时，分别以梁单元和非线性弹簧单元来模拟管片和纵缝接头.

1.3 水土压力

本文工程实例的土质主要为标准贯入数大于8的黏性土和砂质土，参照文献［14］的建议，采用分算模式计算水土压力.对于分算的水土压力往往等效为图3a所示的上下矩形、两侧梯形的荷载，然而对于大直径盾构隧道，上述简化将引起较大误差.图中，ps与qs分别为横向和竖向土压力，pw和qw分别为横向和竖向水压力，qg为管片重力等效均布荷载，R0为隧道半径.对比荷载模型Ⅰ，Ⅱ，Ⅲ可知，模型Ⅲ更合理地考虑了水压力和拱背土压力的影响，本文选择图3c的模型Ⅲ来计算水土压力.

对于竖向土压力，当上覆土厚度为15～30m（1.0倍直径至2.0倍直径）时，采用全覆土模型计算；当上覆土厚度为35m时，按成拱效应后的太沙基土压力模型计算；侧压力系数根据地质资料取值.

图3 水土压力分布模型Fig.3 Distribution model of water and soil pressure

本文共计算两组不同埋深衬砌结构进行比较，一组为均质地层条件（饱和重度为18.0kN·m-3，侧压力系数为0.5）；另一组为非均质地层条件，地层情况如表1所示.

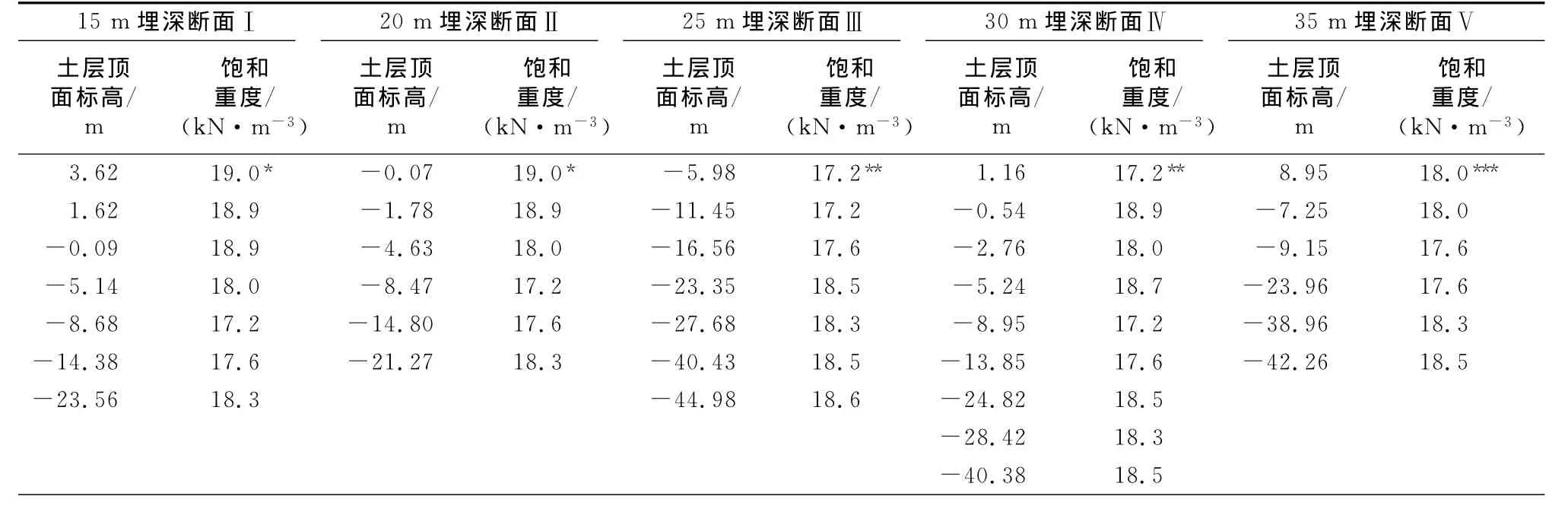
表1 各断面地层分布Tab.1Ground condition of each cross section

1.4 地层弹簧

地层弹簧刚度可根据不同土质按照经验取值.然而该参数与隧道半径相关，文献［11］给出了考虑隧道半径影响的地基弹簧刚度的解析解，即

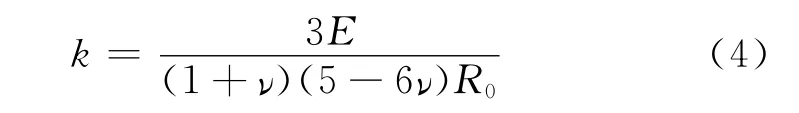
式中：k为地基弹簧刚度；E为地基弹性模量；ν为泊松比；R0为隧道外半径.参考沿江通道工程地质勘查报告，取土层平均回弹模量为15MPa，静止侧压力系数为0.5（对应泊松比为0.33），可得地基弹簧刚度约为1 500kN·m-3，进一步考虑注浆后周围土层的刚度提高，可取地基弹簧刚度为2 000kN·m-3；若根据文献［6］所给出的地铁隧道地基弹簧刚度的经验值再按照半径之比进行折减，则可得到地基弹簧刚度为4 000kN·m-3.因此本文在这一范围之内取2 000，3 000，4 000kN·m-3三个值，用以讨论地基弹簧刚度对于计算结果的影响.此外，根据文献［14］建议，地基切向弹簧刚度取为法向刚度的1／3.

有限元模拟中，以单向受压杆来模拟轴向地基弹簧的作用，切向弹簧为双向受力杆件.

1.5 纵缝接头模型

本文只考虑纵缝接头的转动刚度，文献［9］给出了与本文具有相同尺寸和构造形式的纵缝接头试验所得内力-变形关系（见图4），其表达式为

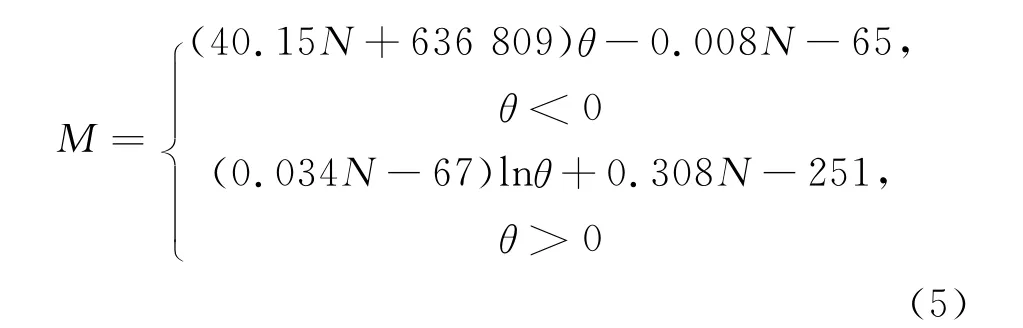
式中：M为接头弯矩；θ为接头相对转角；N为轴力.基于该试验结果，本文重新拟合得到

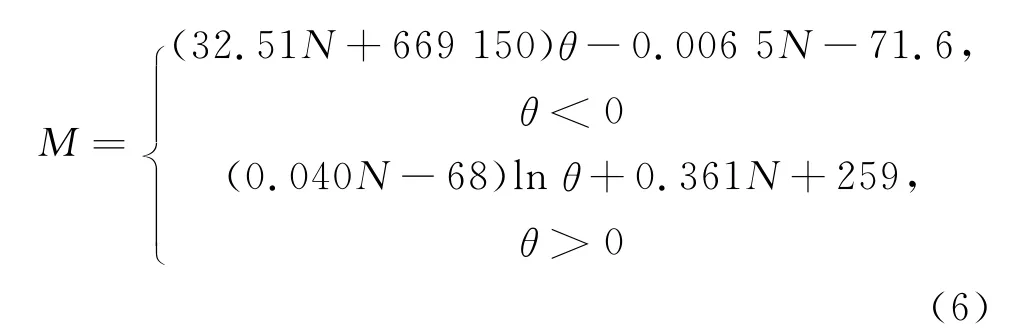
由于是否考虑接头处的刚度折减对于轴力计算结果影响并不大，因此，可由均质圆环梁模型计算轴力.此外，在埋深不变的情况下，衬砌结构的轴力沿全周变化相对较小，而弯矩变化幅度较大，同时接头转角也主要受到弯矩影响，因此，取计算断面轴力平均值代入式（6），即可得到该轴力水平下的转角-弯矩模型，如图5所示.相对于文献［15］中所提出的双折线模型，上述模型能够反映接头由未张开状态到变形快速发展状态的过渡过程.

图4 纵缝接头内力-转角关系Fig.4 Relationship between inner force and rotation angle of longitudinal joint

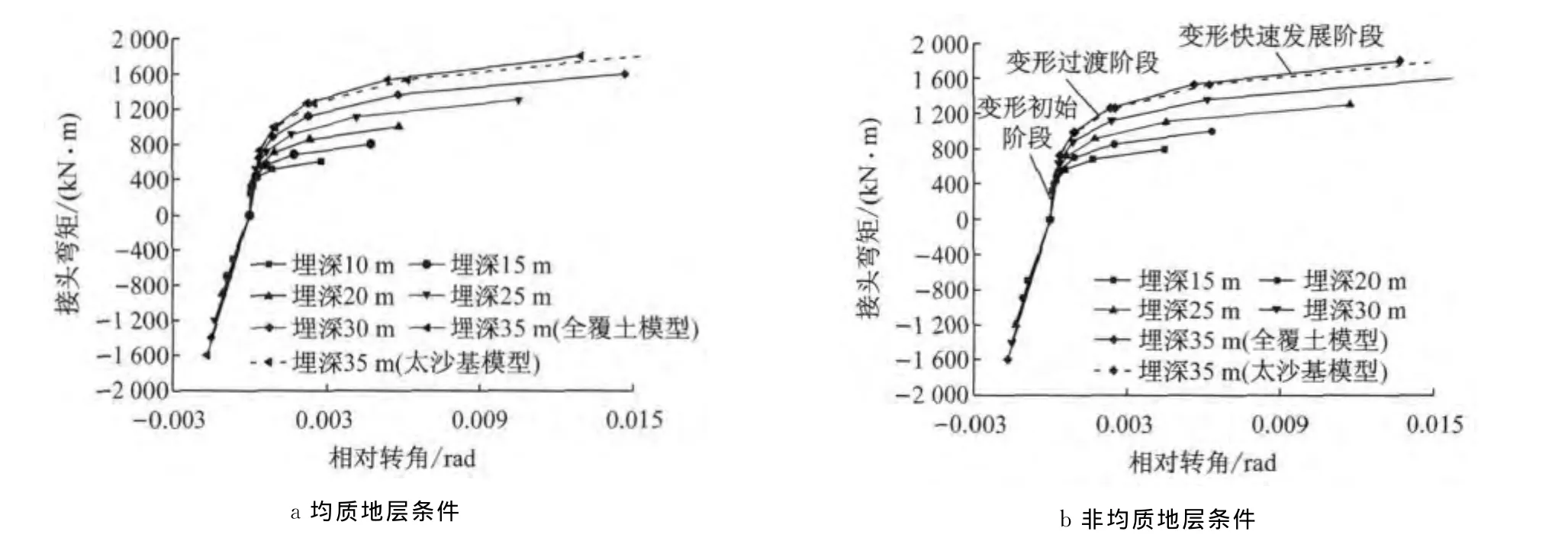
图5 不同埋深情况下的接头转角-弯矩模型Fig.5 Rotation angle-bending moment model at various buried depths

2 计算结果及分析

2.1 单环梁-接头模型计算结果

采用均质圆环模型与单环梁-接头模型计算得到的衬砌结构弯矩、最大横向变形及刚度有效率如图6～8所示.由计算结果可知，当覆土厚度小于1.0倍直径时，刚度有效率变化规律较为复杂，其值为0.88～0.90，远大于其他埋深断面；覆土厚度为1.0倍直径时，结构刚度有效率则相对较低；覆土厚度超过1.0倍直径后，横向刚度有效率整体上体现出先增大后减小的趋势，当轴向地基刚度在2 000～4 000kN·m-3范围内取值时，横向刚度有效率为0.58～0.75，并且随着地基刚度取值的提高，横向刚度有效率也有所提高；当覆土厚度超过2.0倍直径时，土压力按照全覆土模型计算较按太沙基模型计算所得的刚度有效率更小.

结构的横向刚度有效率主要受纵缝接头不连续变形发展程度的影响，而接头变形主要受内力分布控制.由计算结果可知，结构在不同埋深条件下呈现出3种弯矩分布形式，如图9所示.分布形式Ⅰ对应于覆土厚度小于1.0倍直径的结构，分布形式Ⅱ对应于覆土厚度为1.0倍直径的结构，分布形式Ⅲ则对应于覆土厚度大于1.0倍直径的结构.

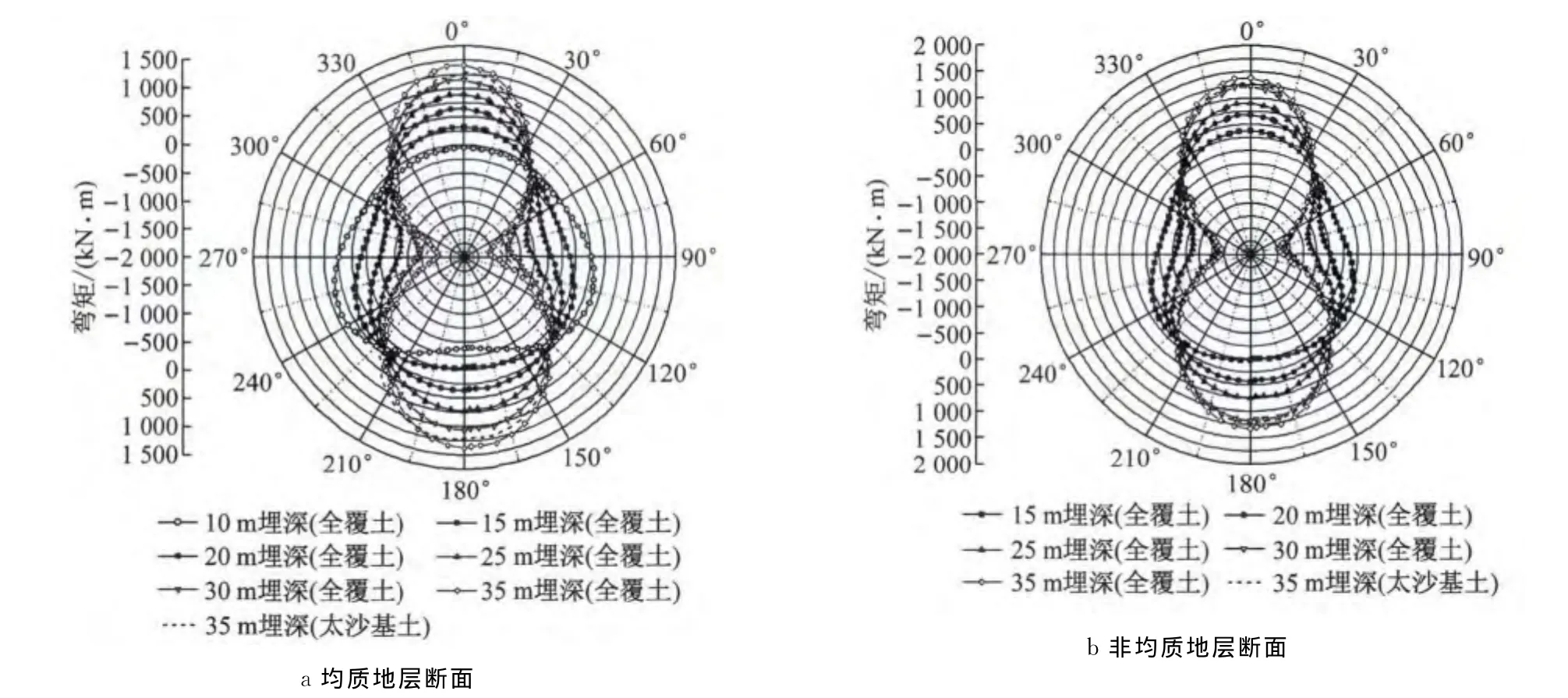
图6 不同埋深情况下的结构弯矩对比（地基刚度2 000kN·m-3）Fig.6 Comparison of structural bending moments at various buried depth （foundation stiffness 2 000kN·m-3）

图7 单环梁-接头模型计算得到的结构最大横向变形Fig.7 Maximum lateral deformation obtained by single beam-joint model

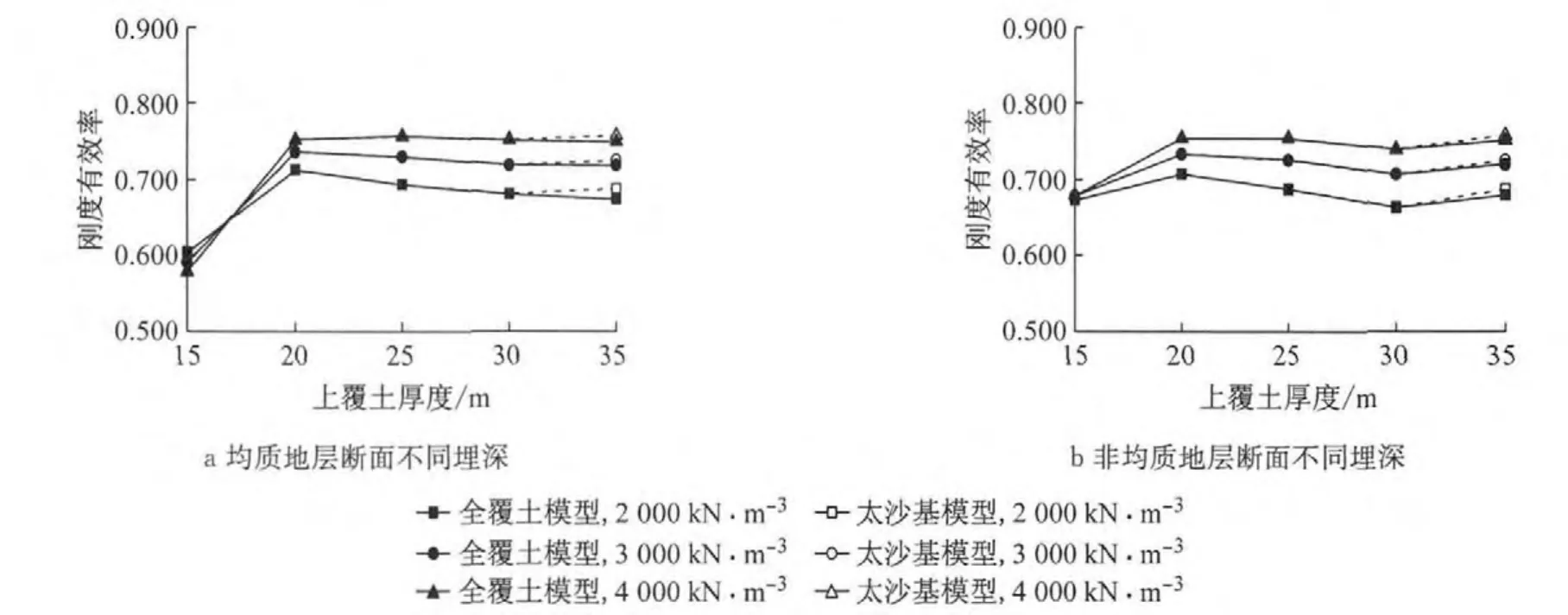
图8 单环梁-接头模型计算得到的结构横向刚度有效率Fig.8 Lateral stiffness efficient obtained by single beam-joint model

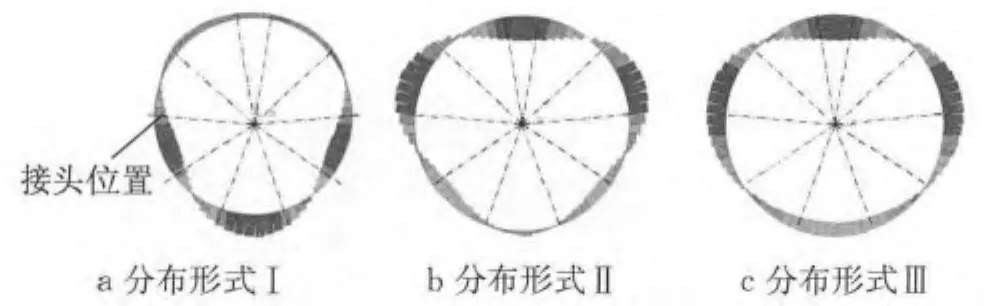
图9 典型弯矩分布形式Fig.9 Distribution of typical bending moment

覆土较浅时，环顶和环底都没有出现集中的正弯矩，由于纵缝接头负弯矩刚度较大，因此此时纵缝接头不连续性造成的影响很小，横向刚度有效率有所提高.

对于弯矩分布形式Ⅱ的结构，其下部两侧都有弯矩集中区且纵缝接头处于该范围内，因此结构受纵缝接头非连续性的影响较大，相应地出现了该埋深条件下刚度有效率较低的情况.

当埋深达到一定深度以后，弯矩呈现出分布形式Ⅲ，此时随着埋深增大，作用于纵缝接头上的轴力与弯矩随之增大.由图5所示的纵缝接头力学模型可知，轴力对于转动刚度的提高作用主要在变形的过渡阶段，在转动变形快速发展阶段，不同轴力条件下的转角-弯矩曲线斜率近似平行；埋深较浅的结构中弯矩更趋近于转动变形初始阶段或者过渡阶段，埋深较大的结构则更趋近于转动变形快速发展阶段.因此，基于横向变形等效原则计算得到的刚度有效率总体将随埋深呈减小趋势.

当覆土超过2.0倍直径后，由于太沙基土压力模型考虑了地层成拱效应，土压力增长速度放缓，结构的弯矩增长幅度小于轴力增长幅度，抑制了接头的刚度降低趋势，因此刚度有效率不再继续减小，甚至略有提高.

需要指出的是，结构横向刚度有效率随深度的变化规律同样受土质条件的影响.本文所考察的均匀地层和非均匀地层中的结构横向刚度有效率也呈现出一定差异.

2.2 错缝双环梁-接头模型计算结果

采用均质圆环模型与错缝双环梁-接头模型计算得到的衬砌结构弯矩、最大横向变形及刚度有效率如图10～12所示.由计算结果可知，错缝双环梁-接头模型计算所得的最大横向变形与刚度有效率随埋深的变化规律与单环梁计算所得规律基本一致，但刚度有效率有一定程度的提高，并且横向变形与刚度有效率随埋深的变化更为平缓，即错缝拼装效应能够减弱埋深条件不同对于结构刚度有效率的影响.当地基弹簧刚度在2 000～4 000kN·m-3范围内取值时，覆土厚度10m时的刚度有效率为0.92～0.94，覆土厚度超过1.0倍直径后的刚度有效率为0.70～0.81.

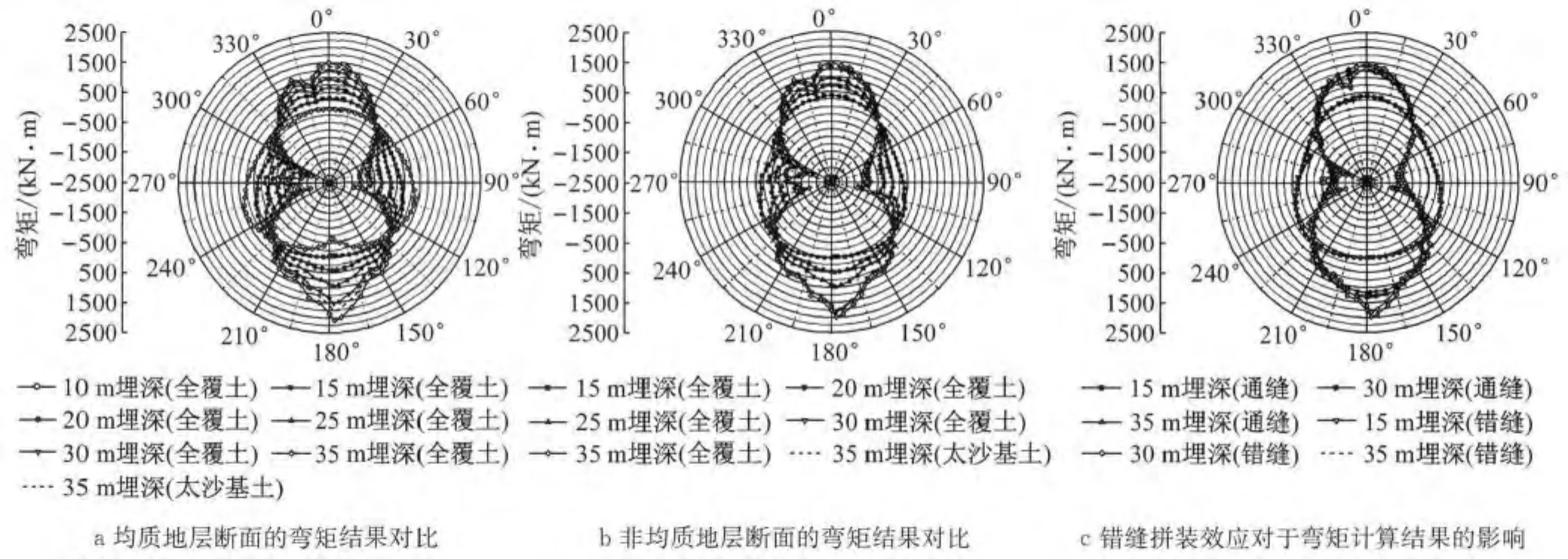
图10 不同埋深情况下的结构弯矩对比（地基刚度2 000kN·m-3）Fig.10 Comparison of structural bending moments at various buried depths（foundation stiffness 2 000kN·m-3）

分析可知，对于采用错缝拼装的衬砌结构，管片在接头位置处的相邻环补强效应限制了变形发展，随着埋深的增大，接头也更难于进入变形快速发展阶段，因而是刚度有效率提高以及随埋深变化更为平缓的主要原因.

2.3 分析

地基刚度、错缝拼装对横向刚度有效率的影响列于表2和表3.由结果可知，地基刚度从2 000kN·m-3变化至4 000kN·m-3对于刚度有效率影响在12%以内.对于浅埋隧道，地基刚度对刚度有效率影响较小，而对深埋隧道影响较大.错缝拼装效应对于结构横向刚度有效率的提高在20.0%以内，并且结构刚度有效率越低，错缝拼装的提高作用越显著.

图11 双环梁-接头模型计算得到的结构最大横向变形Fig.11 Maximum lateral deformation obtained by double beam-joint model

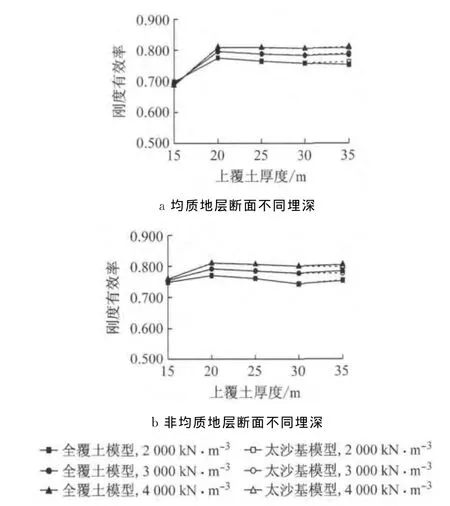
图12 双环梁-接头模型计算得到的结构横向刚度有效率Fig.12 Lateral stiffness efficient obtained by single double beam-joint model

表2 地基刚度对横向刚度有效率影响（以非均质地层断面结果为例）Tab.2 Influence of ground stiffness on lateral stiffness coefficient（for non-homogenous ground section）

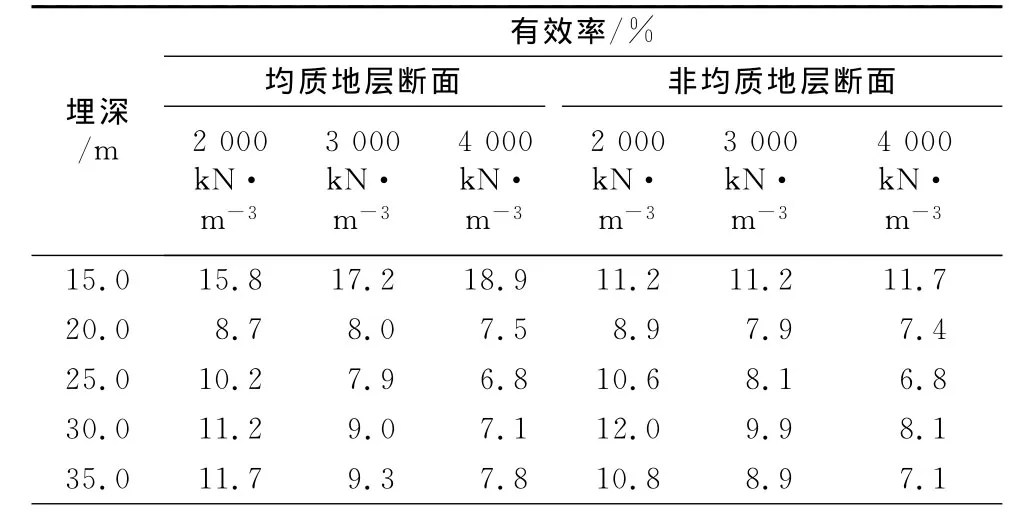
表3 错缝拼装对横向刚度有效率的提高Tab.3 Improvement of lateral stiffness efficient induced by staggered assembling

综上所述，盾构隧道衬砌结构的横向刚度有效率取值与埋深有较大的关系，对于不考虑相邻环补强效应的通缝拼装结构，其横向刚度有效率对埋深更敏感.此外，地基刚度对于深埋隧道有较为明显的影响，计算时建议根据结构的直径参考经验参数和文献［11］的解析方法进行确定.

3 结论

本文依托上海沿江通道工程实例，基于横向变形等效原则，利用结构试验结果的纵缝接头模型，采用数值计算以及理论分析，考察了通缝及错缝拼装的大直径盾构隧道在不同埋深条件下的横向刚度有效率，取得的主要结果有：

（1）大直径盾构隧道的横向刚度有效率随埋深而改变，在覆土厚度大于1.0倍直径时，横向刚度有效率随埋深增大整体略有递减，在埋深达到2.0倍直径后由于地层成拱效应不再继续降低，但在埋深较浅处（1.0倍直径上覆土附近）变化规律相对复杂.

（2）地基刚度取值在2 000～4 000kN·m-3范围，埋深在1.0～2.0倍直径时，本文所考察的结构在通缝拼装形式下横向刚度有效率为0.58～0.75，错缝拼装形式下为0.70～0.81.

（3）地基刚度及错缝拼装对深埋隧道的横向刚度有效率计算结果也有一定程度的影响，两者的提高作用分别在15%和20%范围内.

［1］ 村上博智，小泉淳.シ-の耐荷机构 について［J］.土木学会论文报告集，1978，272：103.

［2］ 朱合华，陶履彬.盾构隧道衬砌结构受力分析的梁-弹簧系统模型［J］.岩土力学，1998，19（2）：26.ZHU Hehua，TAO Lübin.Study on two beam-spring models for the numerical analysis of segments in shield tunnel［J］.Rock and Soil Mechanics，1998，19（2）：26.

［3］ 朱合华，崔茂玉，杨金松.盾构衬砌管片的设计模型与荷载分布的研究［J］.岩土工程学报，2000，22（2）：190.ZHU Hehua，CUI Maoyu，YANG Jinsong.Design model for shield lining segments and distribution of loads［J］.Chinese Journal of Geotechnical Engineering，2000，22（2）：190.

［4］ 苏宗贤，何川.荷载-结构模式的壳-弹簧一接触模型［J］.西南交通大学学报，2007，42（3）：288.SU Zongxian，HE Chuan.Shell-spring-contact model for load and structure interaction［J］.Journal of Southeast Jiaotong University，2007，42（3）：288.

［5］ 彭益成.高水压盾构隧道管片结构非线性性态及流固耦合模型研究［D］.上海：同济大学，2013.PENG Yicheng.Study on non-linear behavior and fluid-structure interaction model for Lining strcture of sheild tunnel under high water pressure［D］.Shanghai：Tongji University，2013.

［6］ 黄宏伟，徐凌，严佳梁，等.盾构隧道横向刚度有效率研究［J］.岩土工程学报，2006，28（1）：11.HUANG Hongwei，XU Ling，YAN Jialiang，etal.Study on transverse effective rigidity ratio of shield tunnels［J］.Rock and Soil Mechanics，2006，28（1）：11.

［7］ 日本土木学会.隧道标准规范（盾构篇）及解说［M］.朱伟，译.北京：中国建筑工业出版社，2001.Japan Society of Civil Engineers.Specification and explanation of tunnel（shield tunnel）［M］.Translated by ZHU Wei.Beijing：China Architecture &Building Press，2001.

［8］ 封坤，何川，夏松林.大断面盾构隧道结构横向刚度有效率的原型试验研究［J］.岩土工程学报，2011，33（11）：1750.FENG Kun，HE Chuan，XIA Songlin.Prototype tests on effective bending rigidity ratios of segmental lining structure for shield tunnel with large cross-section［J］.Chinese Journal of Geotechnical Engineering，2011，33（11）：1750.

［9］ 曹文宏，申伟强.超大特长盾构法隧道工程设计——上海长江隧道工程设计［M］.北京：中国建筑工业出版社，2010.CAO Wenhong，SHEN Weiqiang.Large and particularly long shield tunnel design：Design of Shanghai Yangtze River tunnel［M］.Beijing：China Architecture &Building Press，2010

［10］ 钟小春，朱伟，季亚平，等.盾构衬砌管片环弯曲等效刚度的一种确定方法［J］.地质与勘探，2003，39（增刊）：185.ZHONG Xiaochun，ZHU Wei，JI Yaping，etal.The method to confirm the effective bending stiffness of shield-driven tunnel lining［J］.Geology and Prospecting，2003，39（Supp1.）：185.

［11］ Wood A M M.The circular tunnel in elastic ground［J］.Geotechnique，1975，25（1）：115

［12］ Koyama Y.Present status and technology of shield tunneling method in Japan［J］.Tunneling and Underground Space Technology，2003（18）：145.

［13］ 叶飞，何川，朱合华.考虑横向性能的盾构隧道纵向等效刚度分析［J］.岩土工程学报，2011，33（12）：1870.YE Fei，HE Chuan，ZHU Hehua.Longitudinal equivalent rigidity analysis of shield tunnel considering transverse characteristics［J］.Chinese Journal of Geotechnical Engineering，2011，33（12）：1870.

［14］ 小泉淳.盾构隧道管片设计——从容许应力设计法到极限状态设计法［M］.官林星，译.北京：中国建筑工业出版社，2012.Atsushi Koizumi.Shield tunnel design：From allowable stress design method to limit state design method［M］.Translated by GUAN Linxing.Beijing：China Architecture &Building Press，2012.

［15］ 朱伟，钟小春，秦建设.盾构衬砌管片接头力学分析及双直线刚度模型研究［J］.岩土力学，2006，27（12）：2154.ZHU Wei，ZHONG Xiaochun，QIN Jianshe.Mechanical analysis of segment joint of shield tunnel and research on bilinear joint stiff model［J］.Rock and Soil Mechanics，2006，27（12）：2154.