头部两侧进气道特性分析*
2015-04-15邵跃跃孙振华马高建
邵跃跃,孙振华,马高建
(中国空空导弹研究院,河南洛阳 471009)
头部两侧进气道特性分析*
邵跃跃,孙振华,马高建
(中国空空导弹研究院,河南洛阳 471009)
对一种定几何混压式头部两侧布局进气道进行了三维数值模拟。研究了进气道不同来流条件下的流场结构分布以及这些条件对进气道性能的影响,并与风洞试验结果进行了对比。结果表明,进气道内靠近内侧角部区域激波与附面层干涉比较明显;随着来流马赫数变化,进气道总压恢复系数降低,流量系数上升;攻角状态下进气道内附面层发展较快,对性能影响较大。
固冲发动机;进气道;风洞试验;数值模拟;附面层
0 引言
整体式固体火箭冲压发动机被认为是未来先进战术导弹首选的动力装置,综合了固体火箭发动机和冲压发动机的优点,具有比冲高、重量轻、速度快、系统简单、战勤维护方便等特点。而进气道作为其至关重要的部件之一,直接影响到燃烧室内的燃烧性能及发动机整体性能。关于固冲进气道,国内外开展了大量的数值模拟以及试验研究[1-4],主要集中在采用双下侧混压式进气道的冲压发动机,中心进气与环向进气方式也有相关研究报道[5-6],但对头部两侧进气方式的研究较少。文献[7]只对头部两侧进气固冲发动机的内流场进行了数值模拟,而对采用头部两侧进气固冲发动机的进气道特性没有做出分析。
文中对头部两侧进气道进行了多种工况下的数值计算,分析了不同来流条件、反压对进气道性能的影响,并与风洞实验结果进行了对比。根据计算结果,可以为固冲发动机的进气道设计、一体化数值模拟和发动机的性能优化提供参考。
1 数值模拟
1.1 物理模型
仿真模型是头部两侧进气方式,进气道的扩张段相对较长。关于进气道出口形状,已有研究表明对出口角区进行倒圆处理改为所谓的“肾形”,可以降低补燃室压强和温度,对热防护比较有利,但掺混效果不如“马蹄形”截面[7]。为保证补燃室的掺混及燃烧性能,同时便于网格处理,进气道截面采用“马蹄形”。

图1 头部两侧进气道模型
1.2 数值方法和湍流模型
文中控制方程采用的是基于雷诺平均的三维N-S方程,它的矢量积分形式是:
其中:W是守恒向量;F和G为无粘或粘性通量,为体积力和化学反应源项。控制方程组采用有限体积法进行离散,积分方程则采用一阶迎风格式进行离散,数值求解方法使用收敛性较好的耦合隐式算法。而对于湍流模型的选择,目前所见文献中,多数相关工程问题采用BL代数模型或κ-ω双方程模型,并得到了较为合理的结果。文中采用运用最广泛的标准κ-ω双方程模型。
1.3 网格划分与边界条件
计算流场范围包括外流场、锥形段、初始段和扩张段,而对于进气道的外流场,为了减少网格数及计算量,取弹头表面向外延伸5倍弹径区域,如图2所示。网格生成是流场计算的关键问题,构造一个合理的网格有利于提高计算速度和精度,在内存允许的条件下,尽可能对网格进行加密,为了满足粘性计算和加快计算速度的要求,全部采用结构化网格,并对进气道锥形段和初始段进行局部加密。考虑到来流和远场边界条件的影响,文中仿真计算中使用了3种边界条件:无滑移壁面边界条件、远场边界条件以及压力出口边界条件。

图2 计算网格示意图
2 计算结果分析
由于研究对象是对称体,流动也具有一定的对称性,在不考虑攻角因素影响时,取整个结构的1/4进行计算,如图2所示,而分析进气道的攻角特性时,需要导弹一侧一个完整的进气道模型,取1/2模型进行计算。特性分析中,图表和曲线均取其中最高值进行归一化处理。
2.1 进气道的典型工作状态分析
在H=15 km,Ma=3.0,α=0°,β=0°状态下,改变进气道反压,得到进气道的临界性能。由于进气道的临界状态很不稳定,所以结尾正激波处在喉部附近时,反压值变化不能太过剧烈,否则激波就会被推出口外。
图3和图4是对称面的等马赫数线分布和等压线分布。在进气道内,唇口内唇角小于斜激波后的气流角,在内部产生一道斜激波。这道斜激波打到下壁面附面层,由于激波与附面层的相互作用,造成附面层分离。结尾正激波处同样出现了附面层分离和回流,附面层分离导致气流通道截面面积减小,激波后呈现扁平等马赫数线分布。

图3 对称面的等马赫数线分布

图4 对称面的等压线分布
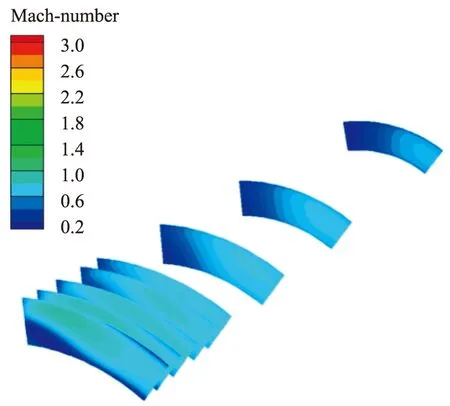
图5 进气道部分横截面马赫数分布云图(1/4模型)
图5是进气道部分横截面的马赫数分布云图。从图中可以看到进气道的马赫数分布受附面层影响比较大,尤其是4个角区域。下壁附面层分离与侧壁附面层分离使得靠近下壁面的角部区域也出现了较强的涡流。靠近下壁面的角区域附面层发展是影响进气道内的流场分布的主要因素,由于进气道截面长宽比较大,附面层发展对进气道内横向的马赫数分布影响比较明显,马赫数分布并不均匀。但因为进气道相对较长、截面面积变化平缓、扩张比较小,进气道出口附近的流场也有很好的均匀性。通过附面层抽吸可以减弱激波与附面层干扰造成的流场不均匀以及通道内的损失,尤其要注意靠近下壁面的两个角部区域。
2.2 节流特性分析
图6是状态Ma=3.2,α=0°,β=0°下进气道流量系数和总压恢复系数随反压的变化曲线图。从图中可以分析知道临界和超临界状态下,进气道的流量系数变化并不大,即使反压很小、出口马赫数出现超音速的情况下,流量系数也基本不变。
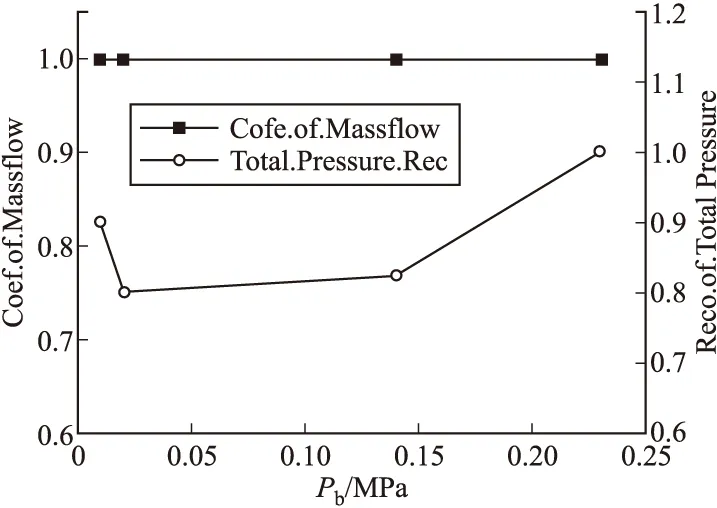
图6 进气道性能参数随反压的变化
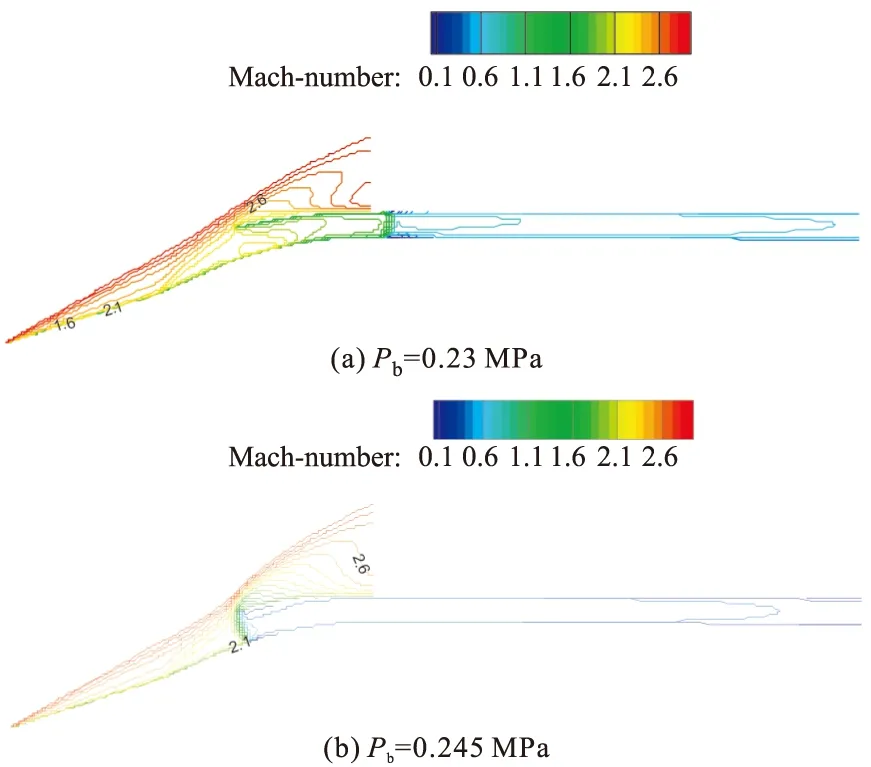
图7 不同反压下进气道对称面等马赫数线分布
图7是不同反压下进气道对称面上的等马赫数线分布图。在反压较小时,出口平均马赫数是超音速,反压影响不到进气道出口截面,总压恢复系数较高。随着反压增大,出现结尾激波,总压损失加大,总压恢复系数急剧下降,而继续增大反压后,结尾激波逐渐被推入喉道段,波前马赫数降低,激波损失也相应减少,总压恢复系数达到最大如图7(a)。反压改变了出口正激波的位置以及波后的流场,但激波前的流场是不变的,所以对流场就不再做太多分析。这里需要说明的是如果继续增大反压,流量系数会急剧下降,这是因为激波被推出口外、出现溢流状态所致,如图7(b)。对于出口马赫数,由于附面层的影响,出口流场是中心区域马赫数较大的不均匀流场,随着反压的增大,出口平均马赫数减小,不均匀程度也降低。
2.3 高度特性分析
通过表1观察不同高度下进气道的性能参数可以发现,马赫数分布情况基本相同,流量系数、总压恢复系数和出口马赫数基本不变。随着工作高度的增加,进气道来流空气静压减小,这样同样马赫数下,来流总压就会大幅度降低,出口反压也明显下降。许多文献中在考虑高度特性时将反压设定为定值,得出出口马赫数必定是下降的,但这种假设与实际不符,意义不大。虽然流量系数基本不变,但出口流量变化很大,这也意味着参加二次燃烧的空气流量减少,必然会导致燃烧室压强下降。在飞行高度高于设计高度时,进气道对反压的敏感程度增强。

表1 不同高度下进气道的性能
2.4 速度特性分析
文中数值模拟了不同来流马赫数下进气道的工作情况,计算高度取15km。在飞行马赫数小于封口马赫数时,进气道口外斜激波并没有封口,存在溢流,再加上侧板溢流,进气道的流量系数比较小。图8给出了进气道流量系数和总压恢复系数随马赫数的变化规律。随着马赫数的增加,外压段激波角减小,溢流减少,流量系数不断增大。而总压恢复系数随着马赫数的增加不断减小,这是由于马赫数增加,口外斜激波强度增加,而且结尾激波前的马赫数也变大,激波损失增强。

图8 进气道性能参数随马赫数的变化
马赫数的增加也使得进气道的流场分布更加复杂,由于参数变化比较剧烈,靠近下壁面的角部区域的附面层分离现象更加严重,进气道畸变增大。所以在飞行马赫数比较大时,更需要加强附面层的控制。
2.5 攻角特性分析
从整体流场来看,头部两侧进气道攻角状态下仍然是对称的,互不影响。由于对称性,进气道正负攻角特性是相同的。
图9是状态Ma=3.0,α=5°,β=0°时的进气道壁面压力分布,根据流动方向,定义图中上部区域为背风侧,下部区域为迎风侧。可以发现结尾激波形状是倾斜的,这是因为在攻角状态下,进气道背风侧的气流折转角变大,激波强度增大,波后马赫数也会减小,这样就导致背风侧区域相比于迎风侧区域在同样的反压条件下,结尾激波位置向前移动。而且通过出口密度和马赫数分布分析知道,流量分布很不均匀,迎风侧区域的流量较大。图10是进气道各截面的马赫数分布,在进气道的角部区域都出现了低马赫数区,观察流线图会发现也出现了如2.1中所说的漩涡,但进气道内的马赫数分布不均匀程度变大,流场也变得比较复杂,对于其附面层的处理显得尤为重要,保证进气道内流场一定的均匀性,以便更好的组织二次燃烧。
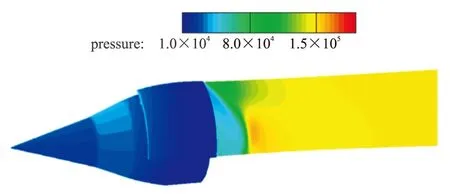
图9 α=5°时的进气道壁面压力分布(1/2模型)

图10 α=5°时进气道部分横截面马赫数分布云图
随着攻角的增加,进气道抗反压能力下降,总压恢复系数也逐渐减小,这不仅是因为存在激波损失,而且由于进气道内出现涡流,增加了掺混损失。关于流量系数,图11给出了进气道的流量系数随攻角的变化规律。当存在攻角时,进气道的来流捕获面积减小,捕获的流量也相应的减少。在α=10°,虽然进气道的流量系数变化不是很大,但进气道内的流场畸变加重,尤其是出口流场,这不利于补燃室的燃烧。
2.6 进气道的风洞试验研究
将进气道的缩比模型安装在高速风洞中,保证边界条件与飞行条件类似,测出风洞中进气道内的压力参数。试验通过调节出口的节流锥的锥位来模拟燃烧室内反压的变化。图12是在来流Ma=3.0,α=0°,β=0°时进气道临界状态下进口前的波系纹影。对比图3同一状态下数值模拟结果,两者基本相同。
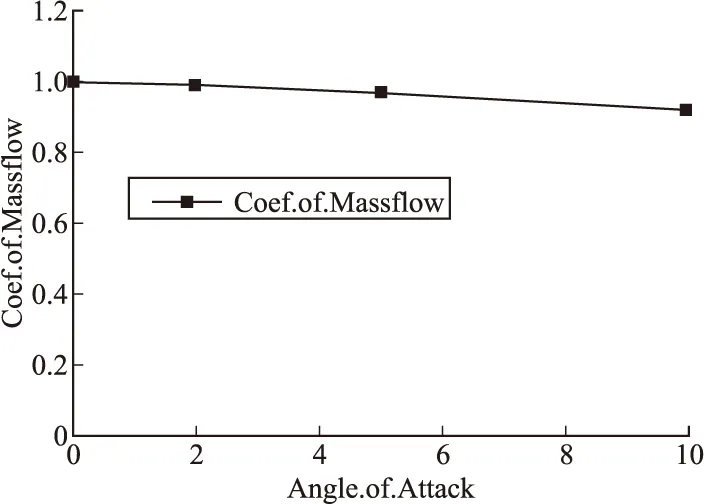
图11 进气道流量系数随攻角的变化

图12 进气道临界状态下进口前的波系纹影
数值模拟得到的来流Ma=3.0,α=0°,β=0°时进气道临界状态沿程压力分布曲线与试验结果对比如图13。其中横坐标是进气道的位置坐标,纵坐标是沿程壁面压力与自由来流压力的比值。静压分布曲线也反映了进气道内波系的分布情况,喉部前压力总体上呈上升趋势,有一些波动主要是由于进气道内的斜激波与附面层作用导致收缩段压力分布不均匀,而且上下壁面压力分布是不同的,图中对比的是上壁面的压力,可以看到数值模拟结果与试验结果吻合较好,说明数值方法是可行的。

图13 进气道沿程压力分布数值模拟与试验对比
3 结论
计算结果与风洞试验吻合较好,表明数值模拟结果是可信的,通过研究得到以下结论:
1)攻角、侧滑角为零时,临界状态下进气道内存在附面层分离现象,尤其是靠近进气道下壁面的角部区域比较明显。角部区域出现涡流,但对进气道下游影响并不大。
2)不同反压下,进气道的流量系数基本不变,在不出现溢流情况下,总压恢复系数随着反压增大而增大。
3)随着来流马赫数的增加,进气道的总压恢复系数不断降低;流量系数不断增加。而高度特性对进气道的总压恢复系数和流量系数影响不大,但对其启动特性影响较大。
4)随着攻角的增大,总压恢复系数、流量系数都是逐渐下降的。由于对称性,正负攻角特性是相同的,但也因为靠近头部,附面层影响较为严重,需要着重考虑进气道的附面层问题,减小附面层对进气道内流场的影响,保证出口流场一定的均匀性。
[1] Galbraith D S, Tunner M G,Orkwis P D,et al. Design of a glass supersonic wind tunnel experiment for mixed compression inlet investigations, AIAA 2010-4728 [R]. 2010.
[2] Sung Hong Gye, Hsieh Shill Yang, Yang Vigor. A unified analysis of ramjet operation in an integrated rocket ramjet engine. Part I: Transition from rocket booster to ramjet sustainer, AIAA 2001-3460 [R]. 2001.
[3] 谢旅荣, 郭荣伟. 双下侧定几何二元混压式进气道的流场特征和气动性能分析 [J]. 航空学报, 2011, 29(3): 257-263.
[4] 李博, 梁德旺. 混压式进气道与弹体一体化流场数值模拟 [J]. 推进技术, 2002, 23(4): 307-310.
[5] 郑凯斌, 陈林泉, 张胜勇. 中心进气式固体火箭冲压发动机试验研究 [J]. 固体火箭技术, 2007, 30(2): 124-127.
[6] 赵春宇, 李斌, 鞠玉涛. 环向进气固体火箭冲压发动机补燃室流场数值模拟 [J]. 弹箭与制导学报, 2008, 28(2): 136-138.
[7] 王希亮, 孙振华, 贺永杰, 等. 头部两侧进气固冲发动机补燃室内流场研究 [J]. 航空兵器, 2011(5): 51-55.
Performance Analysison Bilateral Inlet of Head
SHAO Yueyue,SUN Zhenhua,MA Gaojian
(China Airborne Missile Academy, Henan Luoyang 471009, China)
Three-dimensional flow of fixed-geometry inlet of ducted rocket with a head-bilateral inlet configuration was simulated numerically. The influence of coming flow condition on performance and flow field of the inlet was investigated as well as the results were compared with wind tunnel experiment data. The results show that interference of shock wave and boundary layer is obvious in the corner near underside; With increase of free stream Mach number, the total pressure recovery coefficient decreases, while the coefficient of mass flow ascends; The boundary layer has a great influence on flow field of the inlet with an angle-of-attack.
solid rocket ramjet; inlet; wind tunnel experiment; numerical simulation; boundary layer
2014-08-12
邵跃跃(1990-),男,安徽亳州人,硕士研究生,研究方向:航空宇航推进理论与工程。
V231.3
A
