一种新的十六位置惯性平台自标定方法*

袁爱红,孟卫锋

(航天时代电子公司第16研究所,西安 710100)

一种新的十六位置惯性平台自标定方法*

袁爱红,孟卫锋

(航天时代电子公司第16研究所,西安 710100)

针对目前惯性平台标定误差系数较少的现状,文中探索出一种新的十六位置自标定方法。首先通过分析平台结构和相关安装误差,推导出包含54项误差系数的误差模型;在此的基础上,首次分析了框架轴旋转顺序对系统可观测性的影响;结合平台实际和误差模型,给出了一种新的十六位置自标定方案,并分析了该十六位置相比工程中常用的十六位置的优越性。仿真结果显示该方案可较高精度标定出全部的误差系数。文中提出的标定方案具有易于工程应用的优点。

惯性平台;自标定;误差模型;最小二乘

0 引言

制导工具误差和方法误差是影响导弹命中精度的主要因素,前者占主要成分。而惯性仪表的精度在很大程度上决定了惯性平台系统的使用精度,因此在使用时必须进行补偿,对于高精度惯性平台,对误差进行标定并进行补偿就显得更为重要[1]。目前,对惯性平台系统误差模型的研究,多数停留在对陀螺仪和加速度计误差系数的模型上,而对加速度计和陀螺仪的安装误差考虑的较少。而这些安装误差如果得不到补偿,将会对高精度惯性平台系统的精度产生较大影响[2]。文献[3]讨论了一种可以标定较多误差系数的多位置自标定方法,但未涉及加速度计和陀螺仪的安装误差,标定精度不够;文献[2]、文献[4-8]虽然给出了陀螺仪和加速度计安装误差的标定方案,但未能标定陀螺仪全部的二次项误差系数和加速度计的二次、三次误差系数,也就是标定的误差系数不够多,影响标定精度。

同时,位置的选择是惯性平台多位置自标定的决定性因素,因为位置组合的选择影响误差系数标定的个数和精度[9]。文献[2-8]所给出的位置组合所能估计的误差系数个数非常有限,其本质原因就是这些文章中的位置组合不能使所有的误差系数得到较充分的激励,因此,更好位置组合显得尤为迫切。

文中首先从惯性平台的结构出发,推导出完整的惯性平台系统误差模型;首次分析了框架轴翻转顺序的选择对系统可观测性的影响;在此基础上给出十六位置自标定方案;根据此方案进行仿真验证,并对仿真结果进行必要的分析。

1 惯性平台误差模型

在推导惯性平台误差模型之前,先对惯性平台结构进行简要的说明。文中研究的惯性平台由3个单自由度液浮陀螺仪、3个挠性摆式加速度计组成,3个陀螺和3个加速度计的敏感轴正交安装,分别沿X、Y、Z方向;陀螺仪、加速度计在平台上的安装示意图如图1所示。

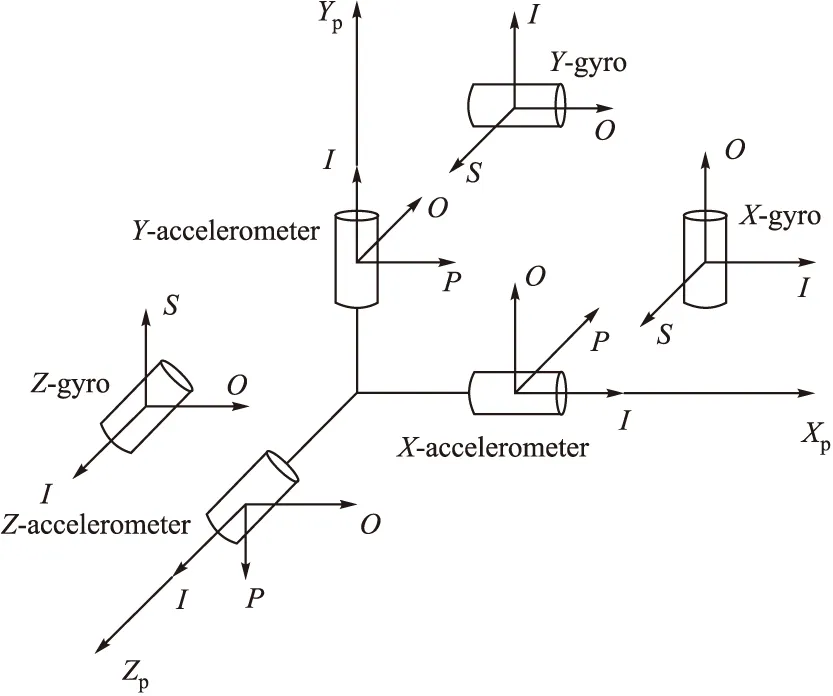
图1 平台组成图

设陀螺仪I轴绕其O、S轴的安装误差为ΔOI、ΔSI,加速度计I轴绕其P、O轴的安装误差为θPI、θOI,I=x,y,z。假定这六个安装误差均为小角度。陀螺仪和加速度计的安装误差分别如图2和图3所示。

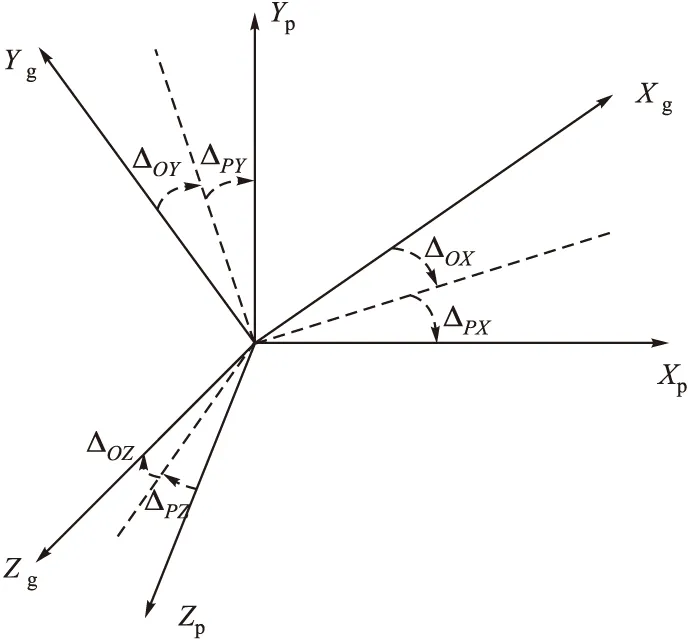
图2 陀螺仪安装误差

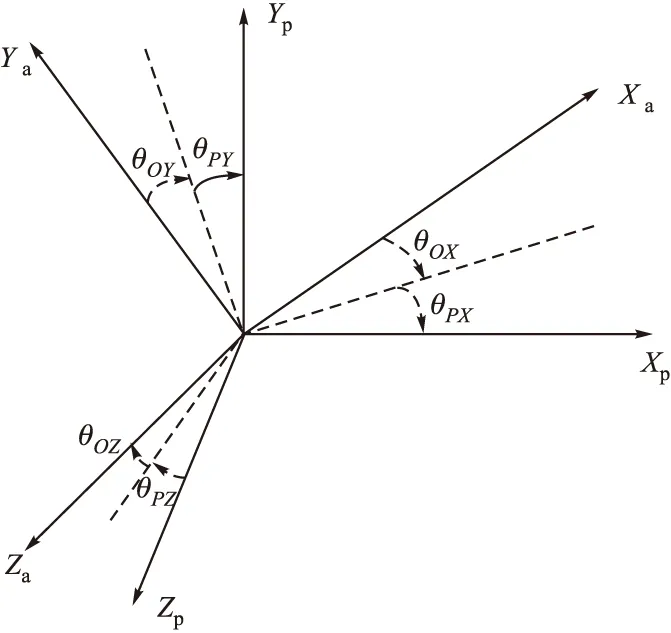
图3 加速度计安装误差

结合图1和图2可得平台坐标系到陀螺仪坐标系的变换矩阵为:

(1)

(2)

(3)

同理,平台坐标系到加速度计坐标系的变换矩阵为:

(4)

(5)

(6)

在翻滚实验中,假定先绕台体轴旋转α,再绕外环轴旋转γ,则地理坐标系n到平台坐标系p的转换矩阵为(假设地理坐标系n为东北天坐标系):

(7)

地球自转角速度在地理坐标系的投影为:

(8)

地球重力加速度在地理坐标系的投影为:

(9)

其中:L0和g0分别表示当地纬度和重力加速度的大小;ωie为地球自转角速度的大小。文中L0取值为34°10′36″,g0取值为9.794 m/s2,ωie取值为7.292×10-5rad/s。

陀螺静态误差模型[10]:

(10)

在静基座条件下,陀螺漂移误差模型为[11]:

(11)

加速度计输出误差模型[10]:

(12)

将式(1)～式(3)以及式(7)～式(9)代入式(10)和式(11)得陀螺仪输出误差模型为:

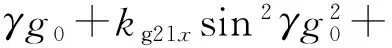
(13)

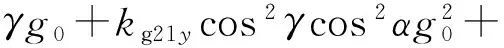
(14)

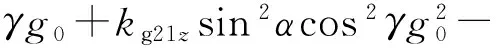
(15)

同理,将式(4)～式(6)和式(9)代入式(12)得加速度计输出误差模型为:

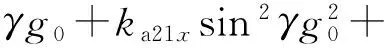
(16)

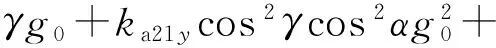
(17)

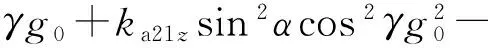
(18)

上述误差模型中一共有54个待估计参数,其中,kg0i(i=x,y,z)是陀螺仪对比力不敏感的静态漂移误差系数,kg1ij(i=1,2,3,j=x,y,z)是陀螺仪对比力一次方敏感的静态漂移误差系数,kg2ij(i=1,2,3,4,j=x,y,z)是陀螺仪对比力二次方敏感的静态漂移误差系数;ka0i(i=x,y,z)为加速度计零偏,ka11i(i=x,y,z)为加速度计标度因数误差系数,ka2ij(i=1,2,3,j=x,y,z)为加速度计二阶非线性误差系数,ka3i(i=x,y,z)为加速度计三阶非线性误差系数。由于待估计参数较多,需要更多的位置才有可能得到较高的估计精度,而同时希望标定时间越短越好,综合考虑这两方面因素,选用十六位置自标定方案。在下一节将探讨惯性平台十六位置自标定方案。

2 十六位置自标定方案设计

在上一节中详细推导了惯性平台系统误差模型,为本节提出标定方案打下基础。在推导误差方程过程中,发现框架轴翻滚顺序对误差模型有一定的影响,而这种影响还没有学者进行深入分析,因此,在本节将首先分析框架轴翻滚顺序对自标定的影响,然后给出十六位置自标定方案。

2.1 翻滚顺序选择

在第一节中给出的陀螺仪和加速度计的误差模型,是假设在多位置翻滚实验中先绕台体轴翻转,再绕框架外环轴旋转。其实框架轴翻转顺序也会对自标定产生一定的影响,因为旋转不同,转换矩阵就会有差异,推导的误差模型也会随之不同,因此分析框架轴的旋转顺序对标定的影响也是很有必要的。假定先绕框架外环轴翻转,再绕台体轴旋转,以x轴陀螺仪为例,由于篇幅限制,不加推导的给出其误差模型为:

(19)

从式(19)可以看出,kg13x和ΔOx的系数成比例,使得这两个参数必有一个不可观或者说在估计时最多能估计出这二者的线性组合。同样对于y、z陀螺仪,均有类似情况出现,这就必然导致可估计参数个数迅速减少;而从式(13)～式(18)可以看出在翻滚实验中先绕台体轴旋转再绕外环轴就可避免参数系数相同或者成比例的情况,也就是说这种翻滚顺序可以提高系统的观测性。

综上分析,可以得出:在多位置翻滚试验中先绕台体轴旋转再绕外环轴旋转可以提高系统的可观测度。

2.2 十六位置方案

分析了旋转顺序是远远不够的,更重要的是位置选择,经验位置无法标定这么多误差系数。研究位置选择实际上是研究系统的可观测性和可观测度。而文中参数估计问题实际上是一个最小二乘估计问题,其数学模型为[12]:

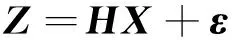
(20)

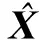
其中M为系统的信息矩阵,其定义式为[12]:

M=HTH

(21)

由最小二乘估计的形式可以看出,当M满秩,也就是可逆时,此时状态变量X的所有分量才能得到估计,也就是系统完全可观测;同时根据最小二乘估计理论知道,对于最小二乘问题(如式(20)),当信息矩阵M某一特征值较小时,信息矩阵的条件数很大,此时最小二乘估计精度很差。矩阵的条件数定义为[13]:

(22)

上式中λ1、λn分别表示量测矩阵H的最大和最小奇异值。也就是说式(22)的值越小,系统的可观测性越好,标定精度越高,标定时间越短,这就为位置选择提供了理论基础,也为实验方案优化设计提供了理论基础。

以x轴陀螺仪为例,若采用十六位置,H的具体形式为:

(23)

将式(23)代入式(21)得M的具体形式为:

(24)

其中:

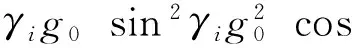
(25)

综合分析误差模型和实际中某些条件的限制,设计了一种十六位置组合如表1。

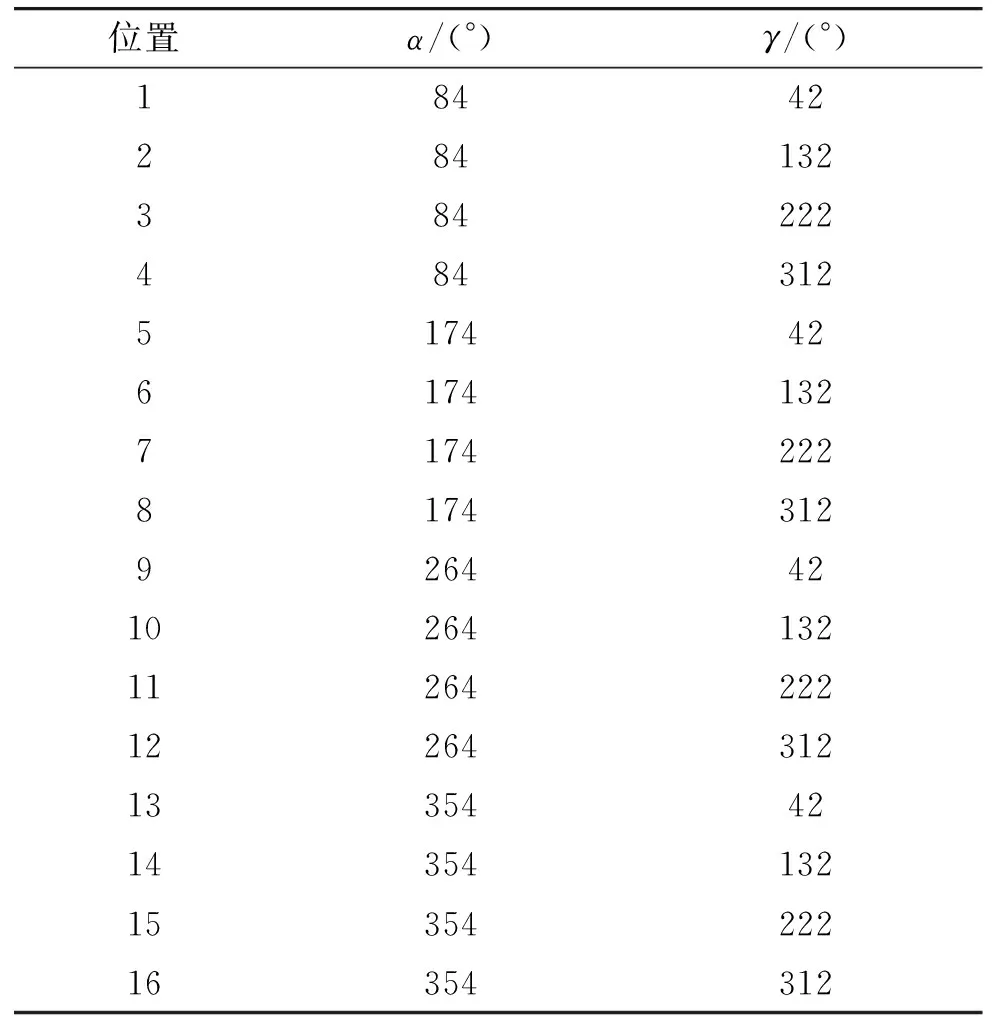
表1 16位置方案

为显示文中选取的十六位置优越性,下面将和工程中其他常用的十六位置进行比较,见表2。

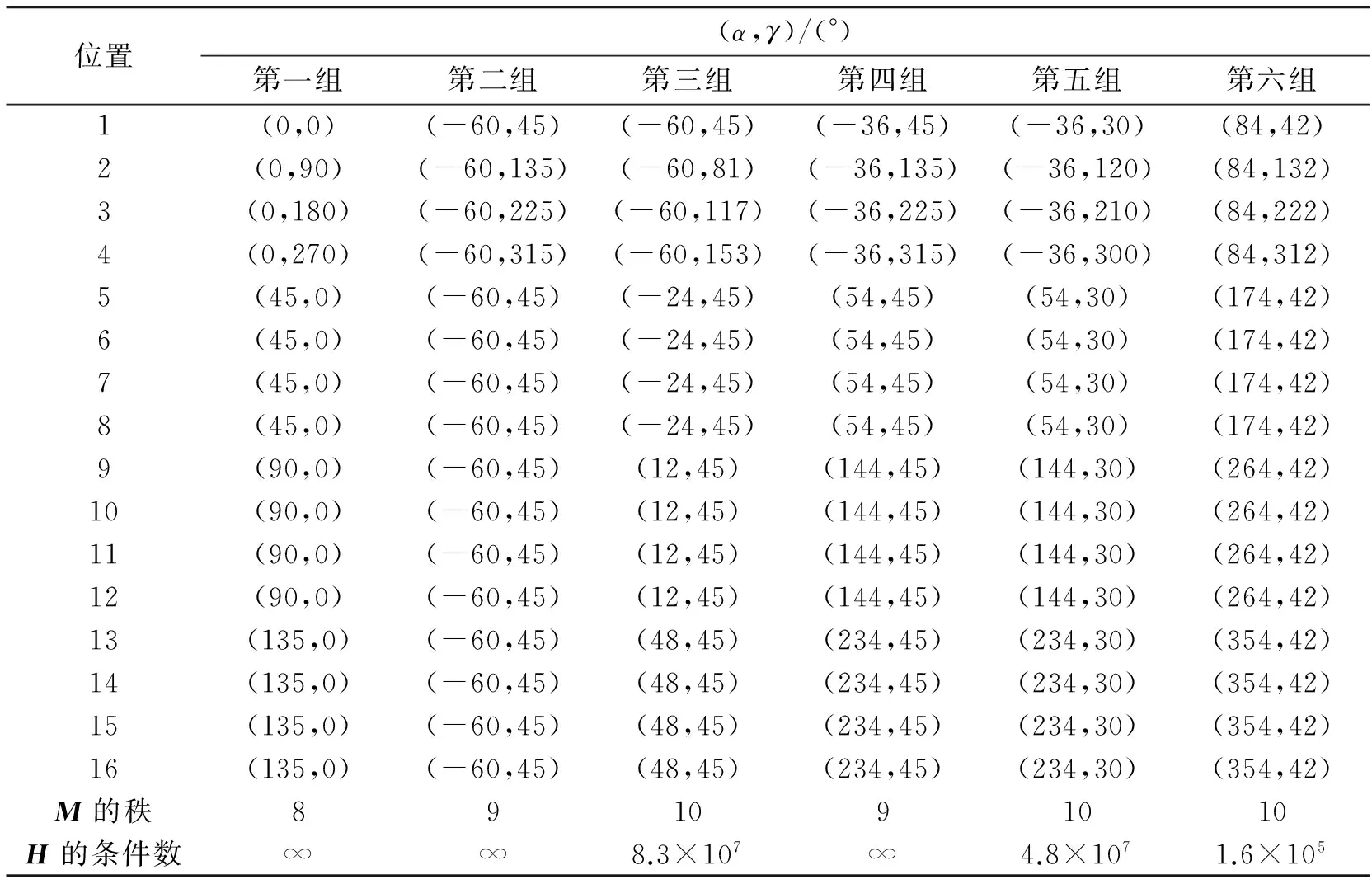
表2 不同位置组合对估计的影响

标定位置的选取对于误差系数的观测性影响很大,只有信息矩阵M为满秩矩阵时,所有系数才可观测;在M为满秩矩阵时,H的条件数越小,误差系数的估计精度越高。从上表可以看出,在上述6组位置中,第三、五、六组的信息矩阵M为满秩方阵,但第六组的观测矩阵H的条件数最小,因此,第六组位置的估计精度最高。实际上,由最小二乘估计理论可知:当条件数的数量级大于105时,即使可以得到估计,但估计误差已非常大,甚至大到无法接受的程度,同时标定时间也会更长,这是惯性平台自标定所不愿看到的。在三、五、六组中,仅第六组条件数在105数量级以内,因此仅第六组位置组合得到的参数估计才是可靠的。第一、二、四的信息矩阵M为奇异矩阵,因此有不可观测状态,也就是说这几组位置组合无法估计出所有的参数,同时由于待估参数有不可观测状态,因此会导致可估计的状态估计精度也很低。

从表2中的数据以及仿真得出最优位置的过程中可以得出如下选择位置的原则:1)外框架轴和台体轴应该避免选择π/2整数倍的位置,因为在这些位置,正弦和余弦以及正余弦的积为零,而观测矩阵H是由正余弦组成的,所以会导致观测矩阵H的很多元素为零,进而信息矩阵M为稀疏矩阵,当要估计的误差系数很多时,信息矩阵M的维数就很高,奇异的概率就更大,主要严重影响二阶误差系数kg2ij(i=1,2,3,4,j=x,y,z)、ka2ij(i=1,2,3,j=x,y,z)的可观测性,这也解释了为什么工程常用的十六位置估计的误差系数少于35个;2)应避免外框架轴和台体轴选择相同的角度,因为相同的角度会使sinαcosγ=cosαsinγ,而这种交叉积在H的同一行中多有出现,这样导致H的列线性相关,进而导致M奇异(因为M=HTH,M的秩等于H的列秩),因此就会导致部分二阶误差系数kg2ij(i=2,3,4,j=x,y,z)、ka2ij(i=2,3,j=x,y,z)不可观测。

3 仿真算例

选用第二节给出的自标定方案,本节将根据第一节给出的误差模型和第二节给出的标定方案(位置组合见表2)进行仿真验证。由于篇幅限制,仅以x轴陀螺仪和x轴加速度计为例进行仿真验证,其他轴与此类似。

在表1所列位置组合下,各陀螺仪及加速度计的各项误差系数将相继受到重力加速度和地球自转角速度的激励。定义相对误差[14]:

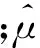
为验证所给定的标定方案优于工程中常见的十六位置标定方案,选择表2中的第三、五、六组位置组合进行比较(其中,第六组位置组合是文中所给出的位置组合),以惯性平台x轴为例,x轴18项误差系数的标定结果见表3。

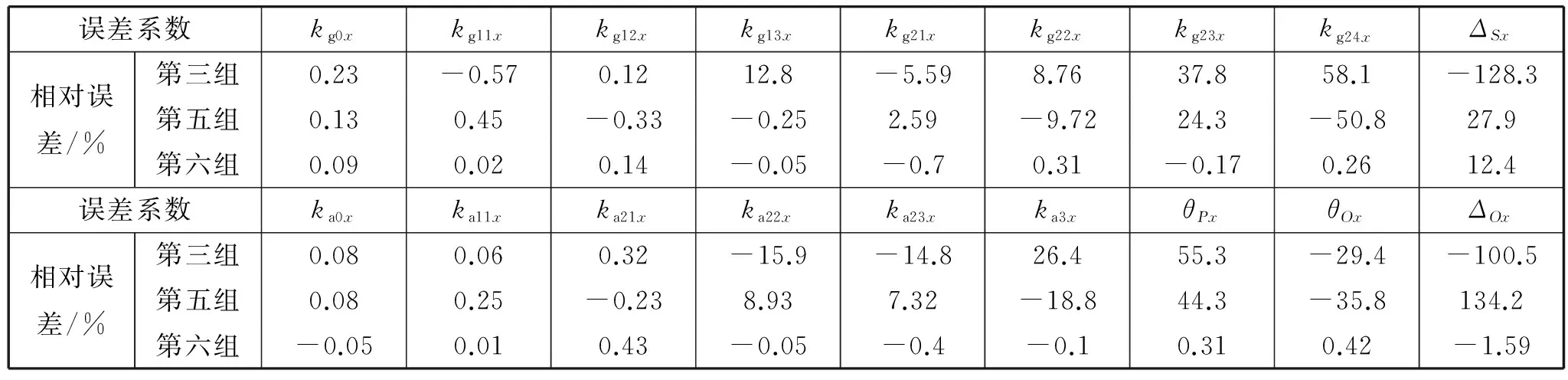
表3 x轴误差系数标定结果

从上表可以看出,文中给出的方案标定精度从整体上看远优于工程中常用的位置组合,这和2.2节分析的结果完全吻合,其原因就是第三、五组的位置组合下的量测矩阵的条件数数量级远超过105,这就导致估计精度很差甚至出现错误。文中给出的位置组合(第六组),在保证所有系数能够被估计出的前提下,还能保证估计精度很高:陀螺仪误差系数估计相对误差最大为0.7%,估计精度高,而安装误差估计相对误差最大达到12.4%,估计精度相对较差;加速度计误差系数估计相对误差最大为0.43%,估计精度较高。陀螺仪安装误差估计精度相对较低的主要原因在于其激励是地球自转角速度,而地球自转角速度相对于重力加速度而言非常小,这使得陀螺仪安装误差的可观测性较差,导致其估计效果不佳。

4 结论

文中首先从惯性平台结构出发并分析了陀螺仪和加速度计的安装误差,详细推导出惯性平台完整的误差模型。在此基础上给出了惯性平台十六位置自标定方案,分析过程及仿真结果中得到以下结论:

1)翻滚实验中,先旋转台体轴,再旋转外框架轴可以在一定程度上提高系统的可观测性;

2)应避开90°整倍数角度位置;

3)尽量避开α=γ的位置。得出标定方案后,对比工程中常用的十六位置组合,比较结果显示文中所选用的位置组合不仅可以估计出全部的误差系数和安装误差(共54项),而且精度最高。仿真结果显示文中提出的标定方案合理,易于工程应用。

[1] 钟万登. 液浮惯性器件 [M]. 北京: 中国宇航出版社, 1994.

[2] 包为民, 申功勋, 李华滨. 惯性平台在系统中多位置翻滚自标定方法 [J]. 北京航空航天大学学报, 2011, 37(4): 462-465.

[3] 刘西河, 宋有山. 任意初始位置平台误差模型自标定 [J]. 中国惯性技术学报, 1994, 2(1): 30-34.

[4] 杨华波, 蔡洪, 张士峰. 高精度惯性平台误差自标定方法 [J]. 上海航天, 2006(2): 33-36.

[5] 杨华波, 蔡洪, 张士峰, 等. 高精度惯性平台连续自标定自对准技术 [J]. 宇航学报, 2006, 27(4): 600-604.

[6] Yuan Cao, Hong Cai, Shifeng Zhang, et al. A new continuous self-calibration scheme for a gimbaled inertial measurement unit [J]. Measurement Science and Technology, 2012, 23(1): 15103-15114.

[7] Zhang H L, Wu Y X, Wu W Q, et al. Improved multi-position calibration for inertial measurement units[J]. Measurement Science and Technology, 2010, 21(1): 1-11.

[8] 曹渊, 张士峰, 杨华波, 等. 惯导平台误差快速自标定方法研究 [J]. 宇航学报, 2011, 32(6): 1281-1287.

[9] 马靖. 高精度惯导平台自标定自对准技术研究 [D]. 长沙: 国防科技大学, 2005.

[10] 秦永元. 惯性导航 [M]. 2版. 北京: 科学出版社, 2014: 9-76.

[11] DENG Zheng-Iong, XU Song-yan, FU Zhen-xian. Identification of coefficients in platform drift error model [J]. Journal of Harbin Institute of Technology, 2002, 9(3): 225-228.

[12] Dan Simon. Optimal state estimation-Kalman, H∞and nonlinear approaches [M]. John Wiley & Sons, 2006: 79-102.

[13] 徐仲, 张凯院, 陆全, 等. 矩阵轮简明教程 [M]. 2版. 北京: 科学出版社, 2005: 52-54.

[14] 欧阳洁, 聂玉锋, 车刚明, 等. 数值分析 [M]. 北京: 科学出版社, 2009: 2-8.

[15] 杨立溪. 惯性平台误差快速自标定技术 [J]. 中国惯性技术学报, 2000, 8(4): 1-4.

A New 16-Position Self-calibration Method for the Inertial Platform

YUAN Aihong,MENG Weifeng

(No.16 Research Institute of China Aerospace Times Electronics Corporation, Xi’an 710100, China)

A new 16-position self-calibration method for inertial platform was proposed in view of lack of method which could estimate a lot of error coefficients. Firstly, through analysis of platform structure and installation error, the error model contains 54 error coefficients was derived. Then, impact of frame shaft rotation sequence for observability of system was analyzed. Combined with actual situation of the platform and the error model, a new 16-position scheme for self-calibration was presented. The simulation results show that the calibrating method proposed in this paper can estimate all error coefficients with high accuracy.

inertial platform; self-calibration; error model; least-square

2014-07-28

总装预研基金;第二炮兵武器装备预研项目资助

袁爱红(1988-),男,湖北十堰人,硕士研究生,研究方向:导航与控制。

V441

A