基于二次曲线拟合的相位编码多普勒补偿研究
2015-04-14杨咚咚屈建社杨辉凤宏晓
杨咚咚 屈建社 杨辉 凤宏晓
(1.陕西黄河集团有限公司 西安 710043;2.总参工程兵第四设计研究院 北京 100085)
0 引言
当前雷达面临着复杂的电磁干扰环境,各种电子干扰不仅雷达信号具有理想的图钉形模糊函数,还要有高的测距、测速精度和好的速度、距离分辨力和单值性等性能指标,而且要有波形捷变能力。相位编码信号通过非线性相位调制扩展等效频宽,可以降低单位频带内的信号能量,同时不易使得敌人察觉。同时,其大时宽带宽积特性很好解决雷达大探测距离和高距离分辨之间的矛盾。此外,其独有的多码型捷变可以保证在每个脉冲之间发射脉冲的随机性,功率谱类似于噪声,具有低截获特性。
相位编码回波信号往往多普勒频移敏感。如果回波信号含有动目标带来的线性多普勒相移调制,由于多普勒调制频率减小了压缩脉冲的峰值,引起失配损失,使得信号检测虚警率增加。已有学者对相位编码信号的多普勒补偿机制进行了研究。卢护林和苏涛[1]通过MTD 处理将不同速度的目标划分为到不同的多普勒通道,然后对各个通道的回波信号进行补偿,然后完成各个多普勒通道的脉压。田黎育和高梅国[2]提出了基于DMTD 的二相码信号多普勒补偿方法,通过DMTD 分离出不同速度目标的回波,然后对不同速度通道的回波信号进行相应步进量的多普勒补偿。张艳艳和宋万杰[3]在分析多普勒失配对脉压影响的基础上,采用500Hz 为步长的13 路补偿技术,根据13 路补偿之后的脉冲压缩结果选大来估算目标的多普勒频率。本论文仅选取三路补偿之后的脉压结果,采用二次曲线拟合真实的目标多普勒频率。
1 m 序列码特性和多普勒频移
相位编码雷达信号是通过对相位离散编码实现的,一般分为二相编码和多相编码。二相编码采用对载波信号相位项进行0、π 调制来实现。多相编码雷达信号比二相编码雷达信号在码字的选择上具有更大的自由度和灵活度,但多相编码雷达信号在实现上较二相编码雷达复杂程度大大增加。故多采用二相编码雷达信号,并多选用伪随机m 序列码型,其伪随机特性表现在:每个码型周期T=2m-1内,0 相位(0 码字)出现的次数为2m-1-1,π 相位(1 码子)出现的次数为2m-1,即为序列的正负码字出现的概率几乎相等。相位编码信号的复数表达式为:
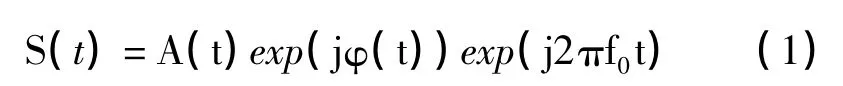
其中,f0为信号的载频,φ(t)为相位的调制项,其二进制相位序列为{φ(t)=0,π},也可以用二进制序列表示为{C=ejφ(t)=0,1}。经过推导[4],相位编码信号经过相关积累后得到脉压输出增益可表示为:
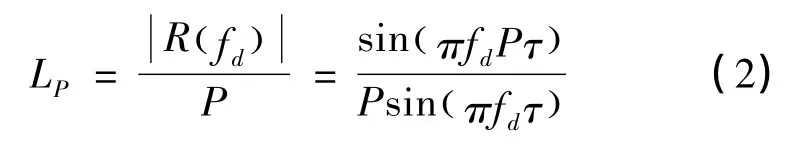
R 为相关积累函数,相关器长度为P,码元宽度为τ。上式中,当fd=0,实现最大相关积累;当fd≠0,存在相关积累增益损失。多普勒频移引起的脉冲压缩输出增益损失图如下,τ=2 ×10-6s,P=128。
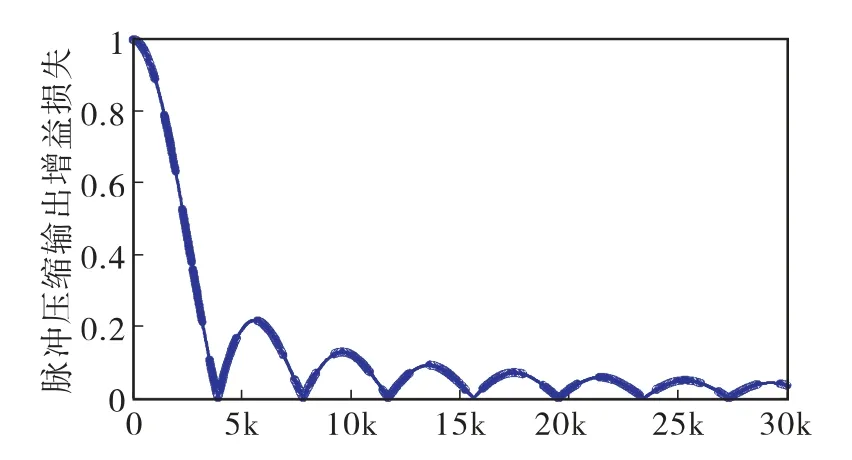
图1 脉压输出与多普勒频移的关系(Hz)
在匹配距离门内,当目标产生的多普勒频移为0,回波信号中的码字与发射信号码字完全匹配,形成同相相加,输出最大信噪比。否则,码字之间不匹配效应增大,不能形成有效脉冲压缩增益。此外,当有多普勒频率存在时,脉冲压缩增益随着多普勒频移的大小呈现一定周期的起伏波动。第一个脉冲压缩增益为零值的区间为多普勒频移容限。
2 二次曲线拟合多普勒补偿机制
从图1 中可以分析得到,多普勒频移容限为4kHz,这对于C 波段雷达的目标速度为100m/s;对于X 波段雷达的目标速度是60m/s。虽然,多普勒容限对应常规波段雷达的目标速度较小。但是,如果我们能够根据雷达系统初步估计出目标速度,使其估计误差限定在多普勒频移容限之内,那么,在多普勒频移容限之内的脉冲压缩输出增益损失曲线在局部就满足二次曲线分布规律,即可以采用简单的二次曲线拟合局部脉冲压缩输出增益损失曲线,从而精确地估计出局部脉冲压缩输出增益曲线的峰值点,计算出目标的精确多普勒速度,实现精确测速和多普勒补偿机制。
多项式拟合问题:已知变量x,y 之间的函数关系为y=a1xn+a2xn-1+…+anx+an+1,通过获得经验样本{ xi,yi|i=1,2,…,m} 来确定出需要拟合的多项式系数(a1,a2,…,an+1)。为保证较好的拟合效果,多项式阶数要取得适当。过低,可能残差较大;过高,拟合模型将包含噪声影响,通常要保证多项式阶数小于经验样本数。这里根据目标速度的初步估计在多普勒容限之内的特点,选取二次曲线拟合。

图2 基于曲线拟合的多普勒补偿技术
在实际雷达系统设计中,往往可以根据不同连续跟踪周期的距离微分实现目标速度的初步估计,并且根据距离微分得到的目标速度的估计值一般均在目标多普勒频移容限之内。图2 是采用二次曲线拟合的相位编码补偿流程框图。其关键点在于首先进行三路补偿fd1,fd2,fd3,然后作脉冲压缩,得到三路幅度信息A1,A2,A3,其坐标关系为{(fd1,A1),(fd2,A2),(fd3,A3)}。根据这三个坐标,求得二次曲线y=ax2+bx+c,采用该曲线拟和脉冲压缩幅度与多普勒频移之间关系局部曲线,如公式(2)所示的多普勒频移容限之内的局部曲线。根据拟和的二次曲线来求得最优补偿的多普勒频移的近似表示。然后根据求得结果,再做一次补偿,然后作一次脉冲压缩。
3 仿真实验分析
为了验证本论文方法的性能,选取如下参数设置来进行实验仿真。ADC 采样率fs=40MHz,二相码长为255,二相码的子码宽度0.25μs,即一个子码采样十个点,脉冲重复周期PRT=512μs,脉冲重复频率fx=1953.1Hz,目标距离通道出现20km,目标多普勒频移设定为3kHz。

图3 采样点跨越真实多普勒频移的二次曲线拟合结果

图4 采样点在真实多普勒频移一端的二次曲线拟合结果
图3 是采样点跨越真实多普勒频移的二次曲线拟合结果,图4 采样点在真实多普勒频移一端的二次曲线拟合结果。图中,实线表示脉冲压缩随着多普勒频移的局部损失曲线,虚线表示采用二阶多项式拟合得到的估计曲线,绿色的点表示采样点数和位置。可以分析得到,图3 中采用二次曲线可以精确地拟合脉冲压缩随着多普勒频移的局部关系曲线,并且根据拟合得到的曲线可以方便地求出真实多普勒偏移量;图4 中,采样点分布于真实多普勒频移的一端,得到的真实拟合曲线与实际脉冲压缩损失曲线有一定的偏移。采样点是估计实际雷达系统距离微分估算得到的,该估算值与不同用途的雷达的测距精度有关,测距精度高的雷达得到的距离微分越接近于实际的多普勒频移量。一般而言,该估算值fd2往往位于多普勒频移容限之内。根据该估算值,前后采用一定的步进量(这里采用±40Hz)来选取另外两个多普勒频移值fd1和fd3。图5 和图6 表示的是数字动目标检测后,目标所在多普勒通道的结果波形,可以看出通过数字动目标检测,分离了带有速度信息的目标回波,但是由于多普勒频移带来了明显的幅度调制,并且信号实部和虚部的调制效应都很明显。
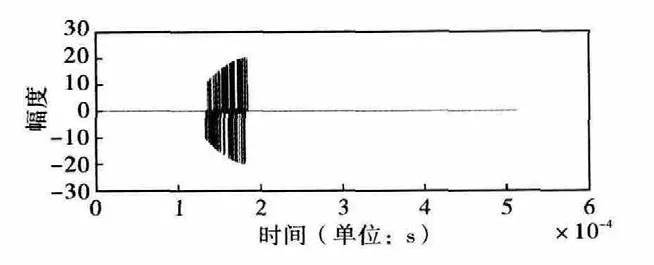
图5 FFT 后多普勒频移补偿之前信号实部
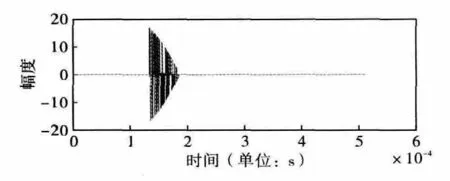
图6 FFT 后多普勒补偿前信号虚部
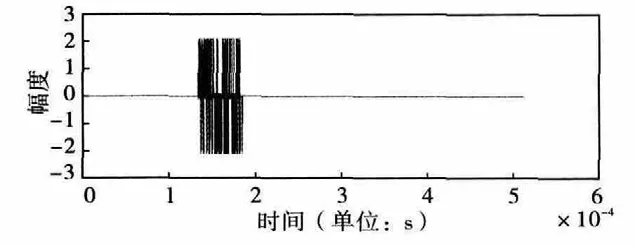
图7 FFT 后多普勒频移补偿之后信号实部
图7 和图8 是对数字动目标检测后的目标回波波形采用基于二次曲线拟合多普勒补偿后的多普勒通道结果。可以明显地看出,该方法通过数字动目标检测(FFT)分离具有一定速度的目标,然后对相应速度通道的回波信号进行相应的三点多普勒补偿,根据补偿之后脉冲压缩三点幅度信息进行二次曲线拟合,从而估计出真实的目标多普勒频移,矫正了多普勒失配的问题。

图8 FFT 后多普勒频移补偿之后信号虚部
本论文限定的条件是实际雷达系统的距离微分得到的目标多普勒估计值小于多普勒频移容限。当然,这对多数雷达系统是满足的。为了验证算法的在不同距离微分估计值情况下,本论文采用二次曲线拟合的综合性能,采用在多普勒频移容限之内随机采样的方式,验证不同位置采样点,所估计最优多普勒频移和已知多普勒之间的统计关系。在多普勒频移容限内随机采样30 次,真实多普勒频移分别采用500Hz,3kHz,10kHz,其它实验参数设置同上,实验结果如下表格所示。如下图9所示,统计均值均接近于真实的多普勒频移值,并且随着真实多普勒频移值的增大,估计值的方差变大,比如10kHz 情况下,大约为200Hz,X 波段雷达目标速度偏差为3m/s。
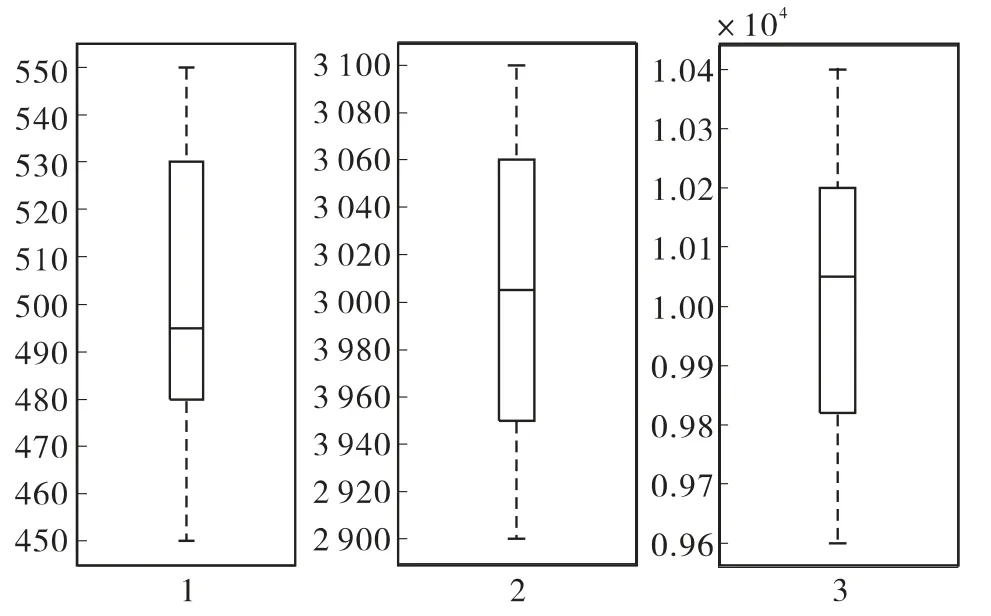
图9 不同多普勒频移估计值的统计盒图分布
4 结束语
相位编码雷达具有的低截获、抗干扰及反隐身特性引起了人们的普遍关注,但是其对于高速运动目标的多普勒频移敏感限制了它的广泛应用[5]。本文研究了一种基于二次曲线拟合的相位编码多普勒补偿技术,根据多普勒频移引起的脉冲压缩输出增益损失局部曲线图近似采用二次多相式曲线拟合,根据拟合的曲线求出最优的多普勒估计值,从而完成最佳的多普勒补偿。本论文方法采用二次曲线拟合,算法简单,易于工程实现,避免无目标的多次多普勒补偿。相位编码技术可以扩展到MIMO 雷达等新体制雷达。
[1]卢护林,冼友伦,苏涛.一种相位编码信号多普勒补偿方法的研究与实现[J].火控雷达技术,2009,38(1):23-25.
[2]田黎育,高梅国.一种二相码信号多普勒补偿方法的研究与实现[J].北京理工大学学报,2002,22(6):757-760.
[3]张艳艳,宋万杰,吴顺君.编码信号的脉冲压缩补偿技术[J].现代雷达,2007,29(9):63-65.
[4]张艳艳.雷达相位编码信号的研究和应用[D].西安:西安电子科技大学,2007.
[5]张剑,周兴建,卢建川.用于高动态目标探测雷达的相位编码脉冲压缩技术,电讯技术[J].2014.
[6]刘铭.基于相位编码的MIMO 雷达的信号处理研究[D].南京:南京理工大学,2014.
