一种基于MTD中间滤波器噪声统计的噪声电平恒虚警方法研究
2015-04-14屈红刚高青松黄金杰
屈红刚 张 强 高青松 黄金杰
(西安电子工程研究所 西安 710100)
0 引言
噪声是限制接收机灵敏度的主要因素。而噪声的来源是多方面的:从接收机内部来说,电路中的电阻、放大器、混频器等都会产生噪声;从接收机外部来说,通过天线引入的天线热噪声、天电干扰、宇宙干扰等[1]。一般情况下,接收机的噪声多用高斯分布表示其统计特性,它是一种钟形对称的分布曲线。具有高斯分布的宽带白噪声经过窄带滤波器后的统计分布通常呈现为瑞利分布。在雷达系统中,经超外差接收机中频放大器后输出的窄带噪声包络也为瑞利分布,在实际工作中,各种噪声会使原本采用固定噪声门限的雷达系统虚警增加,为了使雷达在复杂环境下具有相对稳定的虚警率,本文依据噪声电平统计特性,采用通过统计MTD 中间滤波器噪声的方法,实现噪声电平恒虚警,并将该方法运用于工程应用,验证了其有效性。
1 噪声电平恒虚警处理原理
在不考虑杂波情况下,雷达系统的虚警主要是由系统噪声引起。高斯噪声通过窄带线性系统后,其输出包络的概率密度函数服从瑞利分布:

式中,σ 为检波前高斯噪声的均方值(噪声电压的有效值)。
根据瑞利分布可计算出超过门限VT的虚警概率,即


式中,Vo=VT/σ 为相对门限电压。
由式(2)可得,当门限VT=σ 时,虚警概率Pfa为6.1 × 10-1;当VT= 5σ 时,虚警概率为3.7 ×10-6。可见,在不考虑杂波时,噪声恒虚警门限等于5 倍噪声统计均值时,便可使噪声虚警概率保持在10-6的量级上。
对于瑞利分布来说,不妨引入新变量y=x/ σ,y 的概率密度函数为

式(3)表明,变量y的概率分布与噪声强度无关,如能将变量x 归一化为变量y[2],则噪声强度变化时将保持输出恒虚警。因此,必须设法检测出噪声x的统计平均值,通过相应的电路完成x和σ 相除,便能达到归一化的结果。
瑞利分布噪声的平均值,正比于检波前高斯噪声的均方差,其统计平均值为

由式(4)可知,噪声均值M(x)与方差σ 是线性关系。要使虚警概率Pfa保持不变,则Vo要求保持不变,而Vo=VT/σ,因此,只要VT=σ ×K便可保持虚警概率不变,也就是只要VT=M(x)×K'即可保持虚警概率保持不变,只要实时得到噪声电平值即可实现噪声电平恒虚警。
2 基于MTD 中间滤波器噪声统计的噪声电平恒虚警原理
对于相参积累的脉冲多谱勒雷达系统来讲,杂波一般由于其速度比较小或者为零[4],其多谱勒频率远离MTD 中间滤波器,因此,在无目标时,中间滤波器的输出可以认为就是噪声。虽然偶尔有目标可能落入中间滤波器,但是目标数相对于中间滤波器的数目而言是非常小的,例如,某雷达有1344 个波束,每个波束有大约1500 个距离单元,而每个距离单元中间滤波器数目若取2 个,则雷达扫描一帧中间滤波器的样本数为4032000,而目标在雷达扫描一帧只能出现一次,即使有目标落入中间滤波器,这也不会对噪声电平的统计构成影响。因此,只要实时统计MTD中间滤波器的输出结果,就可以得到系统的噪声电平的均值,噪声电平均值乘以一个合适的系数即为噪声电平恒虚警的检测门限。按照上面的分析,这样的检测门限实际上是随着噪声的变化而变化,因此,该基于MTD 中间滤波器噪声统计的噪声电平恒虚警处理是可以保持系统噪声虚警概率的恒定。
由于噪声电平本身是起伏的,在对噪声电平进行统计时,若统计时间比较短,则统计的噪声电平起伏也比较大,这将会导致雷达噪声虚警率产生比较大的变化[5]。一般情况下可选择一个合适的统计时间段,然后对每一段统计的噪声电平值按照单回路反馈积累的方法对其进行平均估计。该噪声电平恒虚警处理原理框图见图1。

图1 基于MTD 中间滤波器噪声统计的噪声电平恒虚警原理框图
噪声平均值估值[6]按照下式计算:

式中,Z1为存储器中原存储的噪声幅度统计平均值,Zi为雷达新的一次采样得到的噪声幅度统计平均值,Z2为更新后雷达新的噪声幅度统计平均值,K 为小于1 的正数。
一般来说,K 越大,前面输入的作用时间就越长,Z2更新较慢,K 越小,新的噪声电平统计值起作用越快,Z2更新速度较快。为使Z2快速收敛,Z1起始值可用第一次统计平均值。
3 基于MTD 中间滤波器噪声统计的噪声电平恒虚警工程应用
实际工程应用中,某雷达采用16 点相参MTD及-58dB 的切比雪夫加窗处理[7],滤波器组幅频特性见图2。
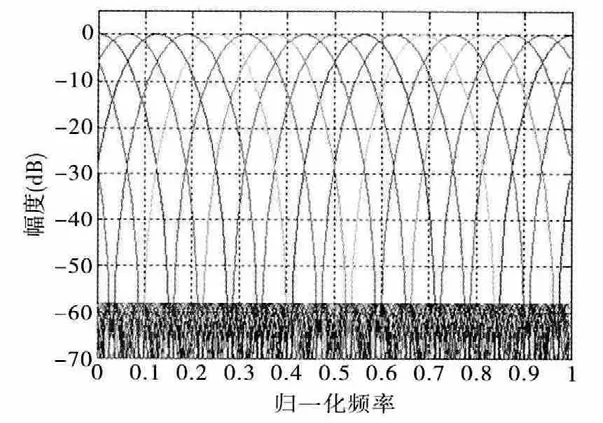
图2 某雷达MTD 滤波器组特性

图3 地物经MTD 处理结果
前面已经分析过,杂波一般主要集中在0 多谱勒滤波器附近,对于某雷达来说,根据脉冲重复频率以及脉冲积累点数来分析,杂波最多展宽到2#和15#滤波器。为此,我们专门采集了一些数据并对其进行了处理,处理结果见图3。该图是地物经过-58dB 切比雪夫加窗后MTD 处理结果,地物目标在0#滤波器幅度为115dB,1#滤波器幅度为109dB,2#滤波器幅度为87dB,14#滤波器幅度为85dB,15#滤波器幅度为107 dB,其他滤波器均小于74dB,也就是说地杂波谱只分布在0#、1#、2#、15#、14#滤波器,没有延伸到3#~13#滤波器。因此,该雷达选取中间8#和9#两个滤波器输出作为噪声电平统计值。
该雷达搜索波束采用了三种脉冲重复频率,每个波束平均距离单元数约为1500 个,每个距离单元选中间的2 个滤波器输出作为噪声电平统计样本,噪声电平每帧(1344 个波束)求一次平均,噪声电平每次统计平均样本量多达4032000 个,噪声电平(归一化后)最大值不超过100,因此,用一个32 位寄存器用于每个噪声电平样本的累加即可满足需要。
该雷达按照图4 的处理流程,对于式(5)所定义的平滑估计模型,系数K 为取7/8;噪声门限系数取5。
下面,我们首先验证一下前面中间滤波器出现目标时对噪声电平统计结果的影响情况。即在没有目标和杂波环境(发射机不开机)下信号处理器实时统计平均噪声电平值,再利用雷达目标模拟器[8]在某个波束的单个距离单元产生一个动目标,其多普勒速度落入8#滤波器,并将每次噪声电平平均值记录下来,结果见表1、2。

图4 基于MTD 中间滤波器噪声统计的噪声电平恒虚警流程图

表1 没有目标和杂波环境下噪声电平统计结果

表2 有一个目标时噪声电平值统计结果
表1,表2 中的统计次数指的是雷达完成整个空域扫描的次数,噪声电平幅度为噪声经过信号处理器处理后实际输出的量化幅度。从以上两组数据来看,中间滤波器偶尔出现目标并不对噪声电平的统计值产生明显影响,这与前面的分析结论一致。
此外,表3 是在雷达不开发射机的条件下(此时系统仅有噪声),采用该噪声电平恒虚警后的系统虚警概率的变化情况。

表3 不开发射机时系统虚警率统计表
从表3 的数据来看,采用门限系数5 得到的虚警概率与理论分析结果基本吻合。
最后,在雷达开发射机的情况下,采取如下措施来验证该噪声电平恒虚警方法的效果。
在天气晴朗且无风的条件下,雷达开机正常,信号处理器不加距离单元恒虚警[3],MTD 低频滤波器0#、1#和15#滤波器加固定的杂波图门限系数,此时,采集系统的虚警概率和MTD 中间滤波器噪声统计值,其关系见图4。从该图上可以看到,虽然发射机工作使得接收机噪声稍微变大,但系统的虚警概率没有发生明显变化,该基于MTD 中间滤波器噪声统计的噪声电平恒虚警处理方法在工程上的应用结果与分析是一致的。
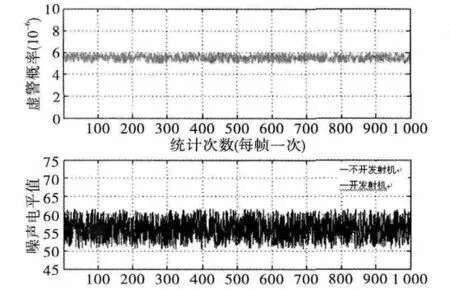
图4 噪声统计值及系统虚警概率变化趋势图
4 结束语
本文从工程应用角度出发提出了采用实时统计MTD 中间滤波器噪声电平的方法,有效减小杂波对噪声电平门限的影响,采用递归算法快速实现了雷达噪声电平恒虚警。该方法已成功应用于某型雷达中。实践证明,该方法实现简单,效果良好,可进行推广应用。
[1]张光义,赵玉洁.相控阵雷达技术[M].北京:电子工业出版社,2006.
[2]李宏等.雷达信号处理恒虚警性能的测试[J].计量与测试技术,2003(3):30-32.
[3]吴顺君,梅晓春.雷达信号处理和数据处理技术[M].北京:电子工业出版社,2008.
[4]李颖,周辉.最大熵谱估计在预测雷达杂波中的应用[J].雷达与对抗,2001,(4):21-25.
[5]李静威,吴桂生,察豪.对噪声干扰的慢门限恒虚警处理分析[J].船舶电子工程,2008,28(4):106-108.
[6]王心福.雷达恒虚警处理对噪声干扰的影响[J].电子对抗技术,2000,15(3):1-6.
[7]李蕴滋.雷达工程学[M].北京:海洋出版社,1999.
[8]肖开健,井伟等.基于DDS 的单脉冲体制雷达目标模拟的实现[J],电子科技,2011,24(11):13-15.
