基于模糊函数频率轴投影的CDMA信号时/频差估计
2015-04-14杨林森张子敬郭付阳
杨林森 张子敬 郭付阳
(西安电子科技大学 西安710071)
0 引言
随着卫星通信技术的飞速发展,地面干扰辐射源对于卫星正常通信的威胁越来越受到广泛的关注,同步轨道双星时差和频差定位技术是一种常见的对地面辐射源定位的技术,已经得到了成功的应用[1]。
同步轨道双星定位中,通常将与目标辐射源直接通信的卫星称为主星,在主星附近辅助定位的卫星称为邻星。由于天线辐射一般具有指向性,主星往往处于地面辐射源的波束主瓣方向内,而邻星常处于波束的某个旁瓣之内。地面辐射源天线主瓣和旁瓣发出的同源信号有且仅有功率的差别,但是由于主星和邻星的位置以及速度不同,地面辐射源发射信号经过两颗卫星分别转发后就会产生时差和频差。双星时/频差定位原理正是通过测量双星接收信号间的时差和频差,再联合地球表面方程实现对未知辐射源的定位[1-3]。
CDMA 信号是一种常用的通信信号,在CDMA信号通信体制内,各用户通过使用相互正交的用户特征码对数字通信内容进行调制,实现了多个用户在相同频段上的同时通信。由于CDMA 各用户信号在时间和频率上相互重叠,各用户信号的信干比很低,导致各用户时/频差的精确估计具有很大困难。另外,由于CDMA 信号带宽较大,相比于一般信号在相同的信号积累时间长度内,采样的数据长度明显增加,导致运算量显著提高。模糊函数是时/频差估计最常用的工具,然而直接计算CDMA 信号的模糊函数所需的运算量过大。为解决CDMA 信号中各个用户相互干扰的问题,在文献[4]中提出利用主星信号逆向分析得到的各用户的重构信号,用重构信号进行估计时/频差。为了解决运算量大的问题,文献[4]根据实际问题中两路信号频差远小于采样频率的特点,对混合积信号进行积分抽取,显著提升了计算模糊函数的速度。
本文在文献[4]提出的利用主星重构信号进行时/频差估计的基础上,提出一种基于模糊函数频率轴投影的CDMA 信号时/频差方法。该方法只需若干次FFT 即可实现,与现有方法对比,在运算速度方面具有显著优势。
1 信号模型
假设主星和邻星接收到的CDMA 基带信号为

其中sk(t)为主星接收到的第k个用户信号,K为用户个数,Δtk和Δfk为邻星接收到相对于主星的第k个用户信号的时差和多普勒频差,n1(t)和n2(t)分别为主星和邻星的噪声。可以看出,邻星接收到的信号为各用户信号经过不同时延和多普勒频移后的线性叠加,且各用户的时差和多普勒频差不同。
对于主星接收信号中的第k个用户信号sk(t),有
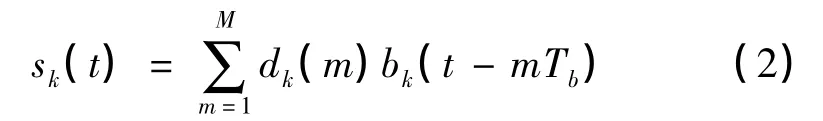
其中dk(m)为用户传输的第m个符号,代表着用户的通信内容,M为用户传输的符号总数,Tb为单个符号持续的时间,CDMA 信号中各用户通过特征波形区分,通信中传输的每一位符号都需要用用户特征波形调整,第k个用户的特征波形为

其中bk(l)为特征波形的第l个码片,Tc为单个码片持续时间,且有Tb= LTc,p(t)为持续时间为Tc的矩形脉冲。为了抑制通信中各用户间的相互干扰,CDMA 信号常用正交伪随机码对各用户的通信内容进行编码。
2 模糊函数在频率轴的投影
两路信号f(t)和g(t)的互模糊函数(Ambiguity function,AF)定义为:

其中τ,v分别为时延和多普勒频率。模糊函数可以认为是信号在时域和频域的二维相关,其峰值位置对应两路信号的时差和频差。然而,当信号较长时,二维搜索模糊函数峰值的计算量过大,难以实时处理。
我们定义Pfg(v)为信号f(t)和g(t)的模糊函数χfg(τ,v)在频率轴上的投影,文献[5]给出了将模糊函数投影到频率轴的快速算法:


其中F(v)和G(v)分别为信号f(t)和g(t)的傅立叶变换。式(5)将计算模糊函数在频率轴上的投影简化为了两路信号自相关乘积的傅立叶变换,因此,计算模糊函数在频率轴上的投影只需要若干次FFT 即可实现。
3 CDMA 信号时/频差估计
由于CDMA 信号中包含有多个用户,且各用户的时/频差不同,直接对主星和邻星接收信号做互模糊函数会产生多峰,当用户时/频差接近时,峰值难以分辨,无法精确估计时/频差。在文献[4]中,通过对主星CDMA 信号逆向分析获取各用户的特征波形和通信内容,将各用户信号进行重构。若将重构的主星各用户信号分别与邻星信号做互模糊函数,能够有效去除用户间的干扰,得到只有单峰的互模糊函数,最终能够提高时/频差估计精度。然而,利用重构的主星各用户信号计算完整的模糊函数,运算量大的问题仍然没有解决。为了减少计算模糊函数的运算量,文献[4]利用现实中多普勒频差远小于采样频率的特点,提出对混合积信号积分抽取的方法来实现CDMA 信号各用户时/频差快速估计,其实质是通过对混合积信号降采样来降低计算模糊函数的运算量。
由于CDMA 信号中各用户的特征码采用相互正交的伪随机编码序列,因而CDMA 各用户发射信号具有尖锐的自相关函数,而各用户间的互相关函数值接近零。对于伪随机序列,其模糊函数为图钉型[6],存在一个很尖的主瓣,主瓣峰值远高于旁瓣高度。若将主星重构的各用户信号与邻星接收信号的互模糊函数在频率轴上进行投影将得到一个具有很高尖峰的曲线,投影的峰值的位置对应原于模糊函数峰值的频率坐标,由投影的峰值位置可以估计出用户双星接收信号的频差,对双星信号补偿频差后通过一次相关,由相关峰位置即可估计出用户双星接收信号的时差。根据上面的分析,利用式(5)可以实现模糊函数在频率轴上投影的快速计算,因此,本文提出了基于模糊函数在频率轴上投影的CDMA 信号时/频差估计快速方法,其具体流程为:
(1),对于主星重构的第k个用户信号sk(t)和邻星接收信号r2(t),按式(5)计算互模糊函数在频率轴上的投影Pskr2(v)。
(2),搜索Pskr2(v)的峰值,记峰值位置为v0,则第k个用户的多普勒频差估计为。
步骤(4),对重构的各用户信号依次按上述步骤处理,直到估计出所有用户的时/频差。
4 仿真实验
假设仿真的CDMA 通信系统中包含8 个用户,各用户使用长度为31 的gold 伪随机序列作为用户特征码。在T=5ms 的信号持续时间内,8 个用户同时进行通信,数字通信符号传输速率为322.58kbps,单个符号的传输时间Tb=3.1μs,每传输一位符号都需要用31 位的用户特征码进行调制,因此用户特征码码片持续时间为Tc=0.1μs,接收信号的采样率为20MHz。双星接收的8 用户CDMA 信号中各用户对应的时延差为[0,0.2,1,-1,2,-4,-0.3,5](μs),多普勒频差为[0,1,50,74,12,-4,6.8,-8](KHz),为了验证本方法的性能,特别选取第一个用户和第二个用户的时/频差参数差距很小。
图1 为主星和邻星接收信号在信噪比为0dB 的情况下互模糊函数的局部仿真图。从图1 中可以明显看出,CDMA 信号的模糊函数为图钉型,存在若干个又高又窄的峰值,每一个峰值对应于一个用户的时/频差。由于第一个用户和第二个用户时/频差相距较近,对应的模糊函数峰值部分重叠而无法清晰分辨,因此图1 中的模糊函数只能看到7 个明显峰值。

图1 双星接收信号的互模糊函数
为了避免用户间的干扰,本文利用从主星接收信号中逆向分析得到的各用户重构信号进行时/频差估计。图2 为第二个用户的主星重构信号与邻星接收信号之间的局部互模糊函数。对比图1 和图2可以看出,由于主星重构信号中只包含单个用户的信号,利用主星重构信号得到的模糊函数只存在单峰且模糊函数旁瓣更低,因此利用主星重构信号能够大大降低各用户间的交叉干扰,进而更准确地估计出各个用户的时/频差。

图2 用户2 主星重构信号与邻星信号的互模糊函数
从图1 和图2 中可以看出,由于CDMA 信号中用户特征码具有伪随机性,CDMA 信号的模糊函数为图钉型,其具有又高又陡的主瓣且主瓣峰值远高于旁瓣高度,因此CDMA 信号模糊函数在频率轴上投影的峰值点将对应其模糊函数峰值点的频率坐标。图3(a)为用户2 主星重构信号与邻星接收信号间的模糊函数在频率轴上投影的曲线。由图3(a)可以看出CDMA 信号在频率轴上的投影将产生一个明显的峰值,根据图3 中峰值的位置,可以估计出第二个用户的频差为0.999 kHz。对双星接收信号补偿频差后再做相关,利用相关峰位置可以估计出该用户的时差。图3(b)为两路信号补偿频率后相关运算结果的仿真图,由相关峰位置可以估计出双星接收信号的时差为0.2μs。利用上述方法,可以分别估计出双星接收的CDMA 信号中各用户的时差为[0,0.2,1,-1,2,-4,-0.3,5](μs),频差为[0,0.999,49.997,73.996,11.999,-4,6.8,-8](kHz)。文献[4]中利用各用户主星重构信号,提出了基于积分抽取的CDMA 时/频差估计方法,而本文在其基础上,利用模糊函数在频率轴上的投影实现CDMA 信号时/频差的快速估计。下面通过对比这两种方法的复乘次数,说明本方法在运算速度上的优势。


图3 CDMA 信号时/频差估计仿真
对于文献[4]中提出的积分抽取算法,假设双星接收信号长度为N且抽取倍数为D,则计算一次混合积信号需要N次复乘,抽取后混合积长度降为N/D,对抽取的混合积做一次FFT 的运算量为N D,计算模糊函数需要重复N次上述过程,则用文献[4]中提出的算法估计时/频差需要的运算量约为。
对于本文提出的算法,同样假设信号长度为N,由式(5)可以看出,计算模糊函数在频率轴上投影只需要计算5 次长度为N的FFT,得到了频差估计后,对信号补偿频率,最后通过相关实现时差估计,本文提出的算法需要的运算量约为5Nlog2N+N+3(2N-1)log2(2N-1)。
对于上面仿真的参数,得到信号长度N=100000,假设文献[4]中的方法使用的抽取倍数为D=100 。表1 为本文提出的方法和文献[4]中的方法在运算量上的对比,可以看出,本文提出的算法在运算量上具有显著的优势,即使当利用文献[4]中提出的算法抽取倍数达到D=100 倍的情况下,本文算法在运算量上仍然具有明显的优势。

表1 积分抽取与本文方法运算量对比
5 结论
针对双星定位问题中,现有CDMA 信号时/频差估计方法运算量较大的问题,本文提出了基于模糊函数在频率轴投影的CDMA 信号时/频差估计方法。针对CDMA 信号模糊函数为图钉型的特点,本文通过求模糊函数在频率轴上的投影即可实现CDMA 信号间时/频差的估计。仿真结果说明本文提出的方法能够快速估计CDMA 信号中各用户的时/频差,相比已有方法,运算量显著减少。
[1]Haworth D P,Smith N G,Bardelli R.Interference Iocalization for EUTELSAT satellites the first European transmitter location system[J].International Journal of Satellite Communiactions,1997,15(3):155-183.
[2]龙宁,曹广平,王勤果.双星时差频差定位系统中的多信号定位技术[J].电讯技术,2011,51(2):16-20.
[3]严航,姚山峰.基于参考站的低轨双星定位误差校正分析[J].计算机仿真,2012,29(10):114-118.
[4]严航,朱珍珍.基于积分抽取的时/频差参数估计方法[J].宇航学报,2013,34(1):99-105.
[5]Sharif M R,Abeysekera S S.Efficient wideband signal parameter estimation using a Radon-Ambiguity transform slice[J].IEEE Trans.on AES,2007,43(2):673-688.
[6]Nadav Levanon,Eli Mozeson.Radar signals[M].New Jersey:John Wiley and Sons,2004:100-164.
