基于位运算的动态多混沌图像加密算法

杨晓刚 王 飞 毛彦斌 薛永才

(1.西安交通大学 西安 710048;2.西安电子工程研究所 西安 710100 3.解放军69220 部队 新疆 842000)

0 引言

随着互联网技术和图像处理技术的快速发展及多媒体技术的广泛应用，图像加密技术对有效保护信息资源将显得更为重要，特别是在军事、医学、航天等领域体现的更加明显。传统加密方法，如:DES算法、AES 算法等虽然在传统的数字加密方面克服了早期加密的诸多弊端，但对像图像、视频这样数据量相对较大的数据来说，加密解密速度慢，不能很好地满足图像传输应用的速度需求。

自1989年英国数学家Matthews 首次提出应用混沌理论进行加密的方法之后，应用混沌理论进行加密体系的设计有了巨大的发展。混沌理论作为一门新兴学科，近年来已经迅速融入到了多个学科，变成重要而前沿的科学［1］。混沌系统具有初值敏感性、非周期性、非收敛性、伪随机性等良好的密码学特性，是非线性确定系统由于内在随机性而产生的外在复杂表现，是一种貌似随机的非随机现象。随着混沌理论的不断发展，各种应用混沌理论进行图像加密的算法层出不穷，很大程度的提高了人们对图像保护的现实需求。因此，数字图像在网络中传输的安全性成为人们关注的焦点，而对于数字图像的加密也成为信息安全中一个重要的研究领域［2-3］。

近年来，很多文献［4］提出低维混沌系统容易遭受分割攻击，图像加密的安全性受到威胁。针对此问题，本文提出了一种基于位运算的动态多混沌映射的图像加密方法。由于在混沌映射迭代过程中采取了扩充控制参数的方法，在一定程度上增加了系统变量的个数，随之相应地使密钥空间增加，从而可以有效抵抗穷举攻击。实验中，我们用Matlab2012软件进行仿真实验，实验结果表明，该算法具有很强的抵御常见攻击操作的能力。

1 基于混沌映射的序列及变换

1.1 混沌序列

因受当前计算机精度限制，混沌序列作为伪随机序列，虽在一定范围内呈现周期性，但考虑到它具有的遍历性高、对初值敏感等特性，目前仍被广泛应用于数字图像加密中。本文通过对两种混沌序列的不同变换达到对原始图像位置置乱和灰度值替换的目的，从而实现对图像的加解密操作。文中用到了具有代表性的混沌序列:Chebyshev 映射和Logistic映射。

Chebyshev 映射定义如公式(1)所示，其中初值x0为(0，1)之间的一个小数，反复迭代公式(1)，得到的混沌序列xn在［-1，1］之间以x轴为对称轴无规律地震荡变化。

Logistic 映射定义如公式(2)所示，其中初值和参数的设置为3.569945＜u≤4，0＜x1＜1，n∈N由此得到的混沌序列xn在［0，1］之间无规律地震荡变化［5］。

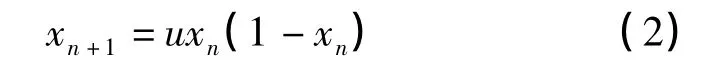
零均值Logistic 映射(亦称抛物线映射)定义如公式(3)所示，其中初值和参数的设为0＜x1＜1，n∈N，由此得到的混沌序列xn在［-1，1］以x轴为对称轴无规律地震荡变化。

以上混沌映射的共同点是当初值x1发生细微变化，且xn大于一定值时，所得结果会出现很大的差别，这个特点体现了混沌映射对初值特别敏感的特性，正是利用这一特性，我们对图像进行加密和解密，提高了算法的安全性。

1.2 伪随机序列

伪随机序列是指用数学递推公式所产生的随机数［6］。文中所用到的序列主要由伪随机序列生成器生成，该生成序列受密钥参数控制(参数控制范围可达到1016)。

1.3 序列变换

数字图像可以看作是由一个个像素点组成的矩阵，其位置和灰度值信息是矩阵的主要内容。实现对矩阵的变换即可实现对图像像素点位置和灰度值的变化。因此，本文旨在将上文提到的混沌序列进行变换来实现对图像中每一个像素点位置置乱和灰度值替换，从而达到对整幅图像像素的加密解密操作。算法基本思想如下:首先，由抛物线序列与输入密钥(汉字序列)经编码运算生成两个混沌映射的原始值，该原始值与控制参数进行简单运算后，将运算后的值作为Chebyshev 映射和Logistic 映射的初始值。其次，对Chebyshev 映射产生的序列进行升序排序，按随机数序列的次序对原始图像各像素进行位置置乱。仿真实验表明，只对图像进行位置置乱，其直方图并没有发生任何变化，很难抵抗统计攻击。因此，还要进行灰度值替换操作。本文加密算法中采取的主要方法如下:给定Logistic 映射初始值，迭代Logistic 映射产生一系列随机数，将随机数乘以1015，然后按照控制参数的方法进行取整，得到一个8 位的整数;然后将该整数各位与控制参数进行比较。大于等于控制参数，将该位置为1，否则置为0，这样就将该整数转化为8 位‘01’串，最后将8位‘01’串转换为0 ～255 之间的整数，这样就生成了一个新的随机矩阵。

1.4 动态灰度值加密方案

基于灰度值加密的方法通常采用传统的静态顺序加密方法。该方法在图像加密过程中不管采用量化方法还是采用排序方法，都不能很好地抵抗明文攻击和统计攻击。如果攻击者针对某一行的数据进行破译并取得成功，那么通过顺序迭代的方法，便能比较容易地破译自此行往下的各行加密像素。而如果采用本文中提出的动态灰度值加密方法，在扩展密钥空间的同时，也增加了攻击者成功破译密文图像的难度。与传统加密方法不同的是，采用本文算法的不足是加密的时间比静态顺序加密方法稍长一些。

2 加密算法

2.1 算法设计

本文算法的主要特点是在像素值替换过程中进一步融入了新的位置置乱，使像素值替换和位置置乱结合起来，增加了破译的难度。加密过程中，我们采取位运算、动态选取行向量等方法，在很大程度上解决了利用混沌系统进行图像加密的一些缺陷，例如:一旦加密图像某行或列被成功攻击，从该行(列)开始的其他行(列)便可轻易地被破解的问题。最后，关于算法的初始密钥也做了特殊设计，即密钥输入不再由数字、字母或数字字母组合构成，而是由一系列的汉字组成，汉字的多少、是否有关联性均由加密者自行设定，这种做法在提升密钥空间的同时也提高了攻击者成功攻击的难度。

本文算法的加密过程如图1所示。解密过程是加密过程的逆过程，这里就不再作详细介绍了。

图1 算法原理图

2.2 算法流程

该算法加密过程可以按以下几个步骤进行:

步骤1:根据外部输入的汉字序列，经密钥系统生成整数k，该值作为零均值Logistic 映射的迭代次数，并将迭代的结果与指定参数进行运算，作为Logistic 映射的初始值;同时，将迭代的结果与输入的汉字序列信息、两个控制参数进行运算，运算后得到的结果作为Chebyshev 混沌映射的初始值。该汉字序列作为算法的一个密钥，其长度和内容均无特殊要求。

步骤2:将Chebyshev 映射产生的随机数进行排序，根据排序结果对原图像各像素进行位置置乱;然后根据随机序列生成器生成的序列，分别逐行抽取置乱结果。随机序列生成器的种子即密钥由16 位的数字组成。

步骤3:对Logistic 映射产生的随机数进行指定倍数的放大、取整后，按照参数要求抽取整数中的指定位数，然后逐位与控制参数作比较，大于等于指定参数将该位置为1，否则置为0，执行完毕后，生成‘01’字符串，将其转换为十进制数。然后，根据序列生成器生成序列对转换结果进行逐行提取。

步骤4:将步骤2 和步骤3 过程产生的结果进行异或，整个过程迭代进行，直至对原始图像像素置乱后的结果逐行抽取结束为止。最后，将整个过程的结果以图像的形式显示出来，即得到最终加密图像。

该算法中用到的一维混沌映射也可用其他低维或高维混沌映射代替，但方法不变，只是对其中用到的参数作局部更换。

解密过程是加密过程的逆操作。首先，通过输入解密密钥生成各映射序列初始值。其次，按伪随机序列生成器生成序列分别对密文图像矩阵和由Logistic 映射经放大、取整等操作结果生成的数字矩阵进行逐行抽取、异或，生成转换矩阵。然后，将转换矩阵元素按Chebyshev 映射序列的排序编号对各元素进行位置还原。最后，将还原后的数值矩阵转换为灰度图像，即为原始加密图像。

3 仿真实验结果

该部分将对算法进行仿真模拟实验，仿真实验中，我们用matlab2012 软件作为开发工具编程实现了所设计的基于位运算的动态多混沌图像加密算法的可行性。本实验分别对不同尺寸、形状的图像进行了实验，如图2、图3 分别列出256 ×256 的Lena图像、512 ×512 的Peppers 图像进行加密和解密算法的实验结果。从实验结果可以看出，该算法对不同尺寸的图像都能正常加密或解密操作。而且，对于不同尺寸的图像，密钥长度可灵活变动，不受图像格式、大小等影响，加密或解密后效果也都比较好。

图3 仿真实验图

4 算法分析

4.1 算法安全性分析

本文提到的算法，首先在密钥的获取上就很难实现突破。攻击者既不知道密钥的长度，也不知道密钥的内容，更不知道密钥具体内容之间是否有联系，要在庞大的中文字库中采用穷举的办法进行尝试，莫过于大海捞针。其次，加密者只需对算法中的部分参数作适当调整，就能成功改变算法的运行轨迹。最后，随机序列生成器的密钥保护也能很好地提升整个算法的安全性。

4.2 密钥空间分析

本文算法采取内外密钥相结合的方式，内部密钥由2 个初始值(抛物线映射的初始值和非线性Logistic 系统的参数)和5 个控制参数组成，其中，3个控制参数均为双精度浮点数，空间足够大。同时，外部密钥是由汉字组成的字符串，其破译难度更大。即使攻击者知道了序列生成器的构成，但由于随机序列的产生由种子控制，种子长度为16 位，因此很难在不知道生成器构成的情况下获取随机序列。就外部密钥(汉字序列)而言，通过穷举法获取密钥，成功的概率是极其微小的。

4.3 密钥敏感性分析

由于混沌系统对初值极其敏感。因此，外部参数的细微变化会导致混沌映射初始值重大变化。从实验分析来看，无论是外部汉字输入密钥，随机生成系统的种子密钥，还是混沌系统的初始值，或是放大、取整、比较时的控制参数均能起到很好的扰乱作用。仿真实验中，我们分别就汉字序列密钥、种子密钥和抛物线序列密钥发生微小变化引起的波动进行分析，其他参数则保持不变。实验结果如图4、图5和图6所示。图4(b)和图4(c)是汉字序列密钥:’我是北京人’的加密解密结果;图4(d)是汉字序列密钥:’我是南京人’的解密结果。图5(b)和图5(c)是种子密钥=［2014，11，18，14，34，56.32］的加密解密结果;图5(d)是种子密钥=［2014，11，18，14，34，56.33］的解密结果。图6(b)和图6(c)是抛物线序列密钥=0.3514213366985417 的加密和解密结果;图6(d)是抛物线序列密钥=0.3514213366985418的解密结果。

图4 密钥F 变化敏感性测试

图5 密钥S 变化敏感性测试

图6 密钥X2 变化敏感性测试

4.4 统计攻击分析

从统计分析的角度来看，一副图像加密效果的好坏从原始图像灰度值分布规律上可以做出评价，所以改变原始图像信息的分布规律就显得特别重要。直方图作为一个重要感性认识的平台，能很好地反映一个算法在抵御统计分析方面是否具有较大优势。如图7所示，从实验结果可以看出，由于进行了位运算、异或等操作，原始图像经过加密后，密文图像灰度值分布比较均匀，使攻击者不能够从统计分析密文图像灰度值分布，达到破解密文图像的目的。

图7 原始图像与加密图像直方图

4.5 像素固定点分析

所谓像素固定点，是指加密前后像素位置或灰度值没有发生变化的那些像素点。很明显，像素固定点越少，置乱效果越好，加密图像安全性越高，抵抗攻击的能力就越强［7］。仿真计算结果:对于一幅256 ×256 的Lena 图像(格式为bmp)来说，像素总数为65536 个，对比实验前后结果发现，加密前后像素位置或灰度值没有发生变化的像素点为254 个，占总像素数目的0.39%，很好地达到了置乱加密的目的。

4.6 加密速度分析

运算速度是衡量图像加密算法性能的一个重要方面，尤其是在实际的网络应用中［8］。该部分针对不同大小的二维图像，分别对本文的加密算法与传统的置乱扩散算法和DES 算法进行比较，实验结果如表1所示。该表反映了与许多传统加密方法相比较，该算法的运行效率还是很高的，更能适应对图像加密实时性的要求。

表1 3 种加密方法效率比较

图8 切割攻击实验结果

5 攻击操作

5.1 切割攻击

切割攻击是图像信息传递过程中常遇到的攻击操作，攻击后的图像往往因部分信息缺失，使恢复过程变得异常困难，本实验旨在分析加密图像进行了切割攻击后的解密效果。图8(a)、(b)、(c)是对Lena 密文图像不同位置进行切割，图8(d)、(e)、(f)则是(a)、(b)、(c)的解密图像。从图8 中可以看出，切割操作虽然对图像造成一定影响，但对解密后的图像来说，原始图像的主要信息并没有缺失，仍然能够辨别出原始图像的主要内容。

5.2 噪声攻击

对于图像而言，加入各种噪声信息，必然会对图像信息的传递带来阻碍。而在日常生活中，常见的图像噪声有椒盐噪声和高斯噪声。实验中，我们用大小为256 ×256 的灰度图像Lena 为测试图，针对椒盐噪声和高斯噪声，我们进行了仿真实验。实验结果如图8所示，图9(a)是密文图，图9(b)和(c)是分别加入高斯噪声和椒盐噪声后的密文图像，图9(d)、(e)和(f)则是相应的解密图像。从实验结果可以看出，两种噪声对密文图像的解密虽有一定影响，但恢复出的图像的主体信息依然明显，效果良好。

图8 噪声攻击实验结果

5.3 滤波攻击

在图像信息处理的过程中，时常会遇到对图像进行空间域的低值、中值滤波，这样的处理方式经常对信息的传输产生干扰。中值滤波相对于低值滤波来说，对算法的抗攻击能力要求更高。在这里，我们以常见的高斯、椒盐中值滤波为例，对加密图像进行滤波攻击操作。实验中，我们用大小为512 ×512 的灰度图像Peppers 为测试图，图9(a)是密文图，图9(b)和(c)分别是高斯滤波攻击和椒盐滤波攻击后的密文图像，图9(d)、(e)和(f)则是相应的解密图像。从实验结果来看，虽然解密图像受到了部分干扰，但主体信息仍得到了较好地保留，原始信息的轮廓依然可以辨识，说明该算法可以抵御滤波攻击。

图9 滤波攻击实验结果

6 结 语

本文分别通过对Logistic 和Chebyshev 两种混沌映射赋予新的应用，同时结合位运算操作，实现了对数字图像的位置置乱和灰度值的动态替换，达到图像加密的目的。文章中对混沌映射结果加倍、放大、取整、比较以及与随机生成器生成序列进行异或，实现了对矩阵范围的有效控制及动态灰度值替换。该算法时间复杂度低，运算成本小，加密速度快，安全性较高。从仿真实验结果来看，本算法也能够有效抵御噪声、剪切等攻击操作，可以满足对图像数据实时加密的要求。

［1］ZHANG Jian，YU Xiaoyang，REN Hong.Image Encryption Algorithm Based on Four-dimension Chaotic Map［J］.Computer Engineering，2008，145(1):145-146.

［2］HAN Zhen-hai，LIU Qiu-wu，LIU Yi.Optical image encryption with rotating invariance based on joint transform correlator ［J］.Journal of University of Electronic Science and Technology of China，2004，33(1):31-34.

［3］HABUSTSU T，ISHIO Y N，SASASE I.A secret cryptosystem by iterating a chaotic map［C］//Advances in Cryptology EU-RCRYPT 91.Berlin:Springer-Verlag，1991:127-140.

［4］赵尔凡，赵耿，郑昊.基于多混沌系统的图像加密算法［J］计算机工程:2012，119(4):119-121.

［5］任洪娥，戴琳琳，张健.基于混沌数列变换的图像加密算法［J］.计算机工程与设计，2013，39(2):26-29.

［6］王瑞胡.计算机中伪随机数生成序列及其在visul C++中的实现［J］.计算机与信息技术:2005，(9):75-76.

［7］王伟.基于Logistic 映射和Chebyshev 映射的快速图像加密算法研究［D］.南京:南京邮电学院，2009.

［8］LIU Le-peng，ZHANG Xue-feng.Image encryption algorithm based on chaos and bit operations ［J］.Journal of Computer Applications，2013，33(4):1070-1073.