基于基扩展的快时变信道建模及仿真①

饶邦国，徐中伟，曹召义

(同济大学电子信息与工程学院，上海201804)

0 引 言

移动通信中，传输的高速率需要更大的带宽，增加带宽会导致采样间隔小于信道的时延扩展，导致信道的频率选择性衰落［1～2］.而移动终端的高速移动，使得多普勒频移增大，信道条件在短时间内发生快速变化，产生时间选择性衰落.因此，对于宽带通信系统而言，快时变信道也就意味着频域和时域的双重选择性.根据以往的研究，基扩展(BEM)信道模型能够比较好的模拟时频双选信道，尤其是在时延大和多普勒扩展的快时变信道［3～4］.BEM模型用有限个基函数的线性组合来描述一定时间内的时变信道(通常为一个传输块).因此，伴随移动通信技术的发展，即要满足超高移动性，又要达到高数据率已经成为通信系统发展的目标.该文给出了某信道的测试参数(运动速度180Km/h，载波频率3GHz，信道采样频率200KHz)［5］，并建立了数学模型，在保证一定的准确度的情况下，把测试数据中的部分数据通过所建模型计算获得，从而减少实际数据的测试量(即利用部分测试数据通过所建模型预测整体数据，实际测试的数据量越少越好).用图表方式展示原始数据与计算结果的误差，并分析模型所用算法的复杂度.

1 信道模型的分析

1.1 多径产生的多普勒效应分析

物体在移动时会造成频率的偏移，也即多普勒频移［6］.各种散射的线路从不同的方位穿插，就有了不同的多普勒频移，最终形成多普勒扩展.基站和物体之间的夹角以及物体的运行速度，可得知多普勒频移为

其中:C 为光速，多普勒频移与列车运动速度V、采样用的频率为fc以及夹角0 有关，越高速度带来越大的多普勒频移，定义最大的多普勒频移为

其中，其中:v 代表物体移动速度，C 代表光速，fc代表载波频率，

1.2 传输模型分析

基扩展(Basis Expansion Model)方法是近来研究的较常见的数学模型，并且为了获得更大的系统性能，可能在以后的实际通信系统中得到大量的应用.该方法的实现，主要是利用有限个基函数，通过它们之间的线性组合来描述一定时间内的时变信道的情况，也可以模拟出有多普勒效应的快时变信道，减少信道参数直接估计的次数，数学模型为:

(3)式中blm是第l 个路径第m 个基系数，在一定时间周期T 内不随时间n 变化，Bm是第m 个基函数矢量，变量是时间n，通过上式，把时变量hl［n］转化为一定时间周期T 内非时变量blm和另一时变量Bm［n］(是时间n 的函数，但函数形式不变)的表达式，即在T 内估计一次blm即可实现对快时变信道参数hl［n］的估算.对于一个传输符号块时间内的信道响应，BEM 系数保持不变，而基函数是随着时间而发生变化的.用BEM 模型来描述信道的时域响应hl［n］，相当于将算法复杂度从NL 降到(M+1)*L［7～9］.

1.3 基于CE－BEM 重建信道

CE－BEM 优点是具有简单的基函数，并且用CE－BEM 模型描述的信道在频域的响应是近似带状的，这种结构在信道估计的时候有非常重要的意义，很多算法都是利用CE－BEM 模型的结构特殊性的优点.

复指数BEM(CE－BEM)采用傅立叶基数来作为基函数，是比较常用的一类的BEM.此时的基函数为:

其中，Wm=2π(m－Q/2)/N，因此，信道的冲击响应可以表示为:

其中，N 代表采样点数，M=Q+1;Q 为BEM 模型的阶数.

2 基扩展信道模式的实现

2.1 模型的理论背景

该文所提供的数据中给出了某信道的测试参数(物体运行速度为180Km/h，载波的频率为3GHz，信道的采样频率200KHz)，我们根据归一化均方误差(NMSE)，其中NMSE 的数学表达式为:

在一定的准确度和算法复杂度的情况下，建立数学模型，其中我们采用了两种不同的思路，一是利用有限个基函数的线性组合来描述一定时间内的时变信道，减少信道参数直接估计的次数，其中我们选择了一种常用的基函数;二是直接采用数据插值的方法模拟接收到的数据，然后再估计出其他数据，其中我们采用了3 种不同的插值函数.其次，将测试数据中的部分数据通过所建模型计算获得，从而减少实际数据的测试量，即在高速运动的快时变信道情况下，用少量的数据来估计快变的信道参数，降低导频的插入频率，从而避免过密的导频插入占用过多的传输资源，以至于降低有用信息的传输速率.最后采用图表方式展示原始数据与计算结果的误差，并分析了建立模型所用算法的复杂度，对几种不同的算法的所得到的结果的误差和所采用的算法复杂度进行了分析和比较.

图1 运动速度为180km/h 的BEM 模型阶数对误差的影响

求出基函数系数blm，最后根据取得的Bm［n］和blm预测其他的数据［10］.另外根据不同的Q 选择相应的数据个数和不同位置的数据，最后根据均方误差(MSE)或归一化均方误差(NMSE)和算法复杂度O(f(n))两个方面评价模型.将(3)改写为矩阵形式为:

其中，hl=［h(0，l)，h(1，l)，…，h(N－l)，l］T，bl=［b0，b1，bM－1，l］T，B 是一个N*M 的矩阵

2.2 模型的实现算法流程

(1)根据已有的数据给出的信道测试参数可知，N=20000，路径M=9;

(2)根据公式(2)(6)，由本可知 V =180km/h，C=3.0*108km/h，fc=3GHz，可得出最大频偏fmax=500.信道采样频率200kHz，因为Q 通常取值为，为取样的时间间隔，并且(Q+1)(L+1)＜N，因此Q 的取值范围不宜超过2000.

该文的建模思路是首先选取复指数CE－BEM模型，由以上1)，2)描述的相关参数求取Bm［n］基函数，和基函数个数M 和Q，其次由公式

根据矩阵公式(8)，我们可以得出基函数系数:

其中:B－1为B 的逆矩阵从文件1 中每个路径中均匀的选取M 个点带入到(9)式中，最终得出我们的基函数系数，并以此模型来预测剩余点数的误差分析.

2.3 模型的分析与评估

下图描述了在不同的BEM 模型的阶数(Q)下，误差的分析图(横轴代表BEM 模型阶数Q，纵轴代表归一化均方误差NMSE):

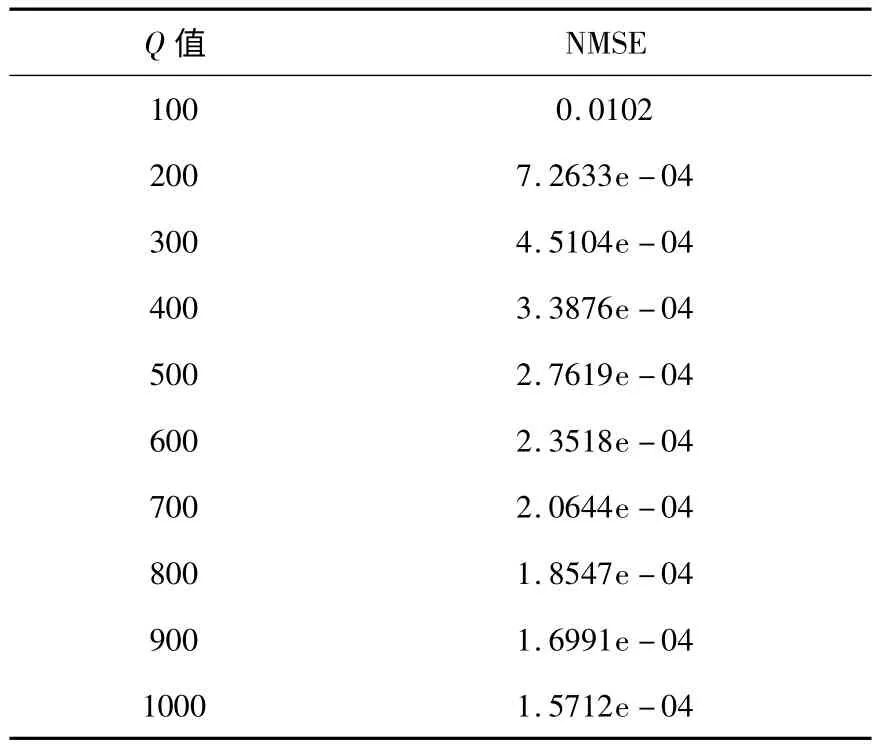
表1 不同Q 值对NMSE 的影响

由上图可以看出当Q 取值为100 时，误差超过0.01，因此虽然此时所需要的采样点数比较少，但是此时误差还比较大，不能满足要求，当Q 取值为200 时，误差迅速下降为小于0.001，因此从模型精确度的标准来看，Q 应该取大于200 的值，因为在Q取值超过200 的时候，误差逐渐减小，但是变化不明显，即此时模型精确度提高不明显，但是随着Q的增加，所选择的数据个数却迅速增加，这样增加了算法复杂度，因此Q 不宜选取大于200 的值，因此综上所述，对于本信道模型来说，Q 的值应当选择200 附近.

3 结 论

该文在研究无线通信中的快时变信道建模过程中采用了两种思想方法.一种方法是根据基函数的方法，构造出了一种信道模型，根据模型评价的两个指标—模型准确度和算法复杂度，对快时变信道进行综合评价，我们发现对于运动速度、载波频率、信道采样频率一定的传输信道模型来说，BEM模型阶数增加，则信道模型精确度提到，但是同时会使测试的数据量增加，当Q 增加到一定值时，模型精确度不再会发生显著变化.

［1］ 吴伟凌等.移动通信原理(第2 版)，电子工业出版社，2009.

［2］ 樊昌信等.通信原理(第6 版)，国防工业出版社，2013.

［3］ 董月.基于Xiao 模型和基扩展模型的高移动性无线信道建模与仿真［D］.成都:西南交通大学，2012，29(3):1－9.

［4］ 李昕.基于基扩展快时变信道模型的OFDM 系统信道估计［D］.西安:西南交通大学，2013.

［5］ 3rd Generation Partnership Project，Technical Specification，36.101(3GPP TS 36.101)，v8.0.0，2007.12.

［6］ 罗志年，张文军，管云峰.不相关Rayleigh 衰落信道仿真模型［J］.系统仿真学报，2009，13:3872－3875.

［7］ Tomasz Hrycak，etc.Low Complexity Equalization for Doubly Selective Channels Modeled by a Basis Expansion.IEEE Trans.Signal Processing，2010，58(11):5706－5719.

［8］ Saptarshi Das.Mathematical Methods for Wireless Channel Estimation and Equalization.Dissertation，University of Vienna，2009.

［9］ Yahong R.，etc.Improved Models for the Generation of Multiple Uncorrelated Rayleigh Fading Waveforms.IEEE Communications Letters，2002，6(6):256－258.

［10］ 汪洋，葛临东.多径独立Rayleigh 衰落信道仿真模型［J］.信息工程大学学报，2007，02:202－205.