一类含参不等式问题的解法探究

姚爱亮

（江苏省盐城市第一中学）

含参不等式“恒成立”与“有解”问题具有覆盖知识点多、综合性强、解法灵活等特点，对培养学生思维的灵活性、创造性有着独到的作用，所以很受命题专家的青睐.解决这类问题主要通过转化成求函数的最值方法解决，然而确定一个含参函数的最值有时比较困难，即使分离参数可能会遇到更复杂的函数，能否予以回避？一般情况下的回答是：否！但笔者发现有一类问题可以借助于切线的特征使问题瞬间简化、巧妙解决.

一、提出问题

二、问题探究

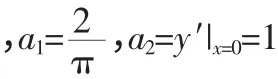
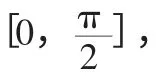
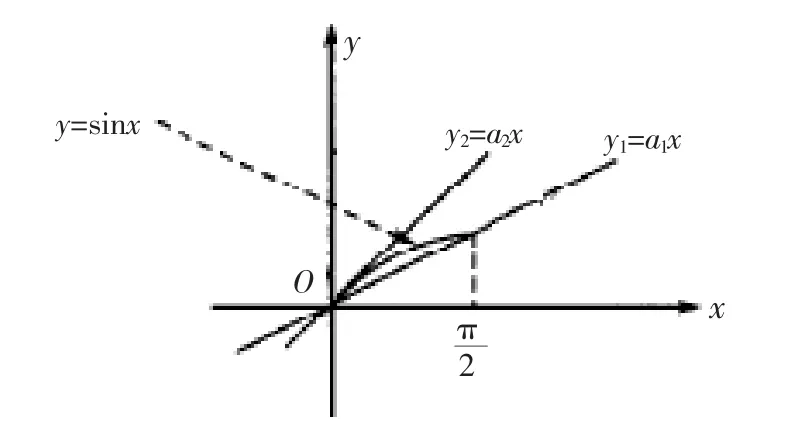
图1

那么函数y=x（a2=1）的作用是什么？它对函数y=sinx 的意义到底是什么？实际上函数y=x 既是函数y=sinx 在原点处的切线，又是函数y=a2x 图象在定义域恒在y=sinx 的上方的一种“临界位置”（如果此时斜率a2再变小就不满足y=a2x 的图象在定义域里恒在y=sinx 的上方）.

结论：利用切线是函数局部图象上（下）方的“临界位置”这一特征可以解决一类含有参数的不等式问题，这一类问题的特征：

（1）已知含有参数的不等式“恒成立”与“有解”问题，求参数的取值范围；

（2）确定含参函数的最值比较困难，分离参数遇到更复杂的函数；

（3）对不等式进行等价转化，可以把两边变成关于变量的两个函数，其中一边是一次函数.

三、解决问题

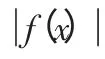
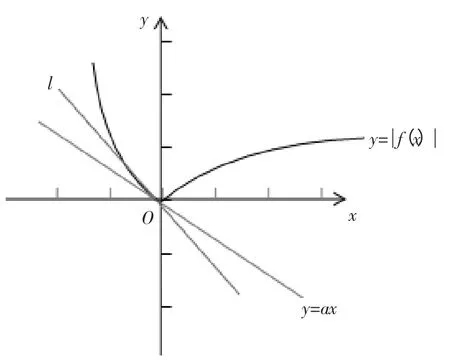
图2

数学能力的提高归根结底还是解题能力的提高. 解题活动一个重要的收获是：如何从具体问题解决过程所反映的思路出发，将节点上的经验或感悟上升为一般的思想方法或一般的解题原则，使之能够帮助我们解决一大类的问题，从而最终达到提升自身解题的能力.