基于Visco-SCRAM模型的侵彻装药点火研究*

孙宝平，段卓平，万经伦，刘 彦，欧卓成，黄风雷

(1.北京理工大学爆炸科学与技术国家重点实验室,北京 100081;2.重庆红宇精密工业有限责任公司,重庆 402760)



基于Visco-SCRAM模型的侵彻装药点火研究*

孙宝平1，段卓平1，万经伦2，刘 彦1，欧卓成1，黄风雷1

(1.北京理工大学爆炸科学与技术国家重点实验室,北京 100081;2.重庆红宇精密工业有限责任公司,重庆 402760)

针对弹体侵彻过程中装药的安全性，基于黏弹性统计裂纹力学(visco-statistical crack mechanics, Visco-SCRAM)模型计算装药整体温升、装药裂纹摩擦生热以及弹体装药与壳体摩擦生热，考察这3种机制对装药温升的贡献以及侵彻装药的点火机制，得到了装药点火对应的弹体侵彻临界初始速度。结果表明：(1)装药与弹体内壁摩擦生热对装药温升有一定贡献，随着弹体初始撞击速度的提高，摩擦生热对温升的贡献逐渐增大；(2)黏性、损伤和绝热体积变化导致的装药整体温升对装药点火的作用有限;(3)裂纹摩擦形成热点是侵彻装药点火的物理机制；(4)采用Visco-SCRAM模型可预测低强度、长脉冲载荷作用下的装药点火响应。

爆炸力学；点火；黏弹性统计裂纹力学模型；侵彻装药；整体温升；裂纹；热点

在弹体对目标的侵彻过程中，装药除承受高速撞击形成的前驱冲击波作用，还要承受持续时间为几毫秒的高惯性载荷作用，极易发生点火反应。这种低强度(压力在1～2 GPa以下)、长脉冲(持续时间在几十μm～ms量级)非冲击加载条件下的点火反应机理与冲击起爆完全不同[1]。非冲击点火是由于材料中有独立的高温区，即热点，材料中应力/冲击波与缺陷间的相互作用形成了这些热点，并且热点的形成与材料的力学、热力学和化学性质等相关。虽然学者们对热点产生的主要机制并没有达成共识，塑性热、局部塑性功、颗粒摩擦、空穴坍塌产生绝热温升、内部剪切和冲击波相互作用是一些细观的机制，但很可能在某种条件下，这些机制都能产生热点。对于侵彻装药，J.K.Dienes等[2]做了温升的数量级分析，认为剪切断裂表面摩擦生热对装药生成潜热起到的作用最大。J.K.Dienes等[3]和Q.H.Zuo等[4]也验证了SCRAM模型计算摩擦生热引起的温度上升能够引发装药点火反应。本文中，基于Visco-SCRAM模型计算装药整体温升、装药裂纹间摩擦生热以及弹体装药与壳体摩擦生热，考察这3种机制在装药温升方面的贡献以及侵彻装药的点火机制。

1 Visco-SCRAM模型简介

广义黏弹性统计裂纹模型由2个模型串联而成：一个是由多个黏弹性体并联而成的广义黏弹性体，另一是由SCRAM模型定义的微裂纹体。下面给出简要计算公式，详细推导过程见文献[2-8]。

(1)

式中：上标n代表第n个体元；N是黏弹性体元数；G为黏弹性体中弹性元的剪切模量；c是微裂纹体元中微裂纹的平均半径；a为初始缺陷尺寸；τ为松弛时间。

(2)

Visco-SCRAM模型中，释放热包括连续介质尺度(宏观)的整体热和微结构尺度(微观)形成的热点。根据一维热传导方程，化学分解是基于Arrhenius一阶化学反应动力学方程，整体温升变化率为：

(3)

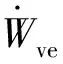
Maxwell体元黏性功率和裂纹损伤功率分别为：

(4)

(5)

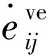
根据裂纹表面滑动摩擦生热来判断热点点火，图1给出了裂纹面热点模型示意图,图中p为静水压力，Smax为最大偏应力，x、y为坐标轴。

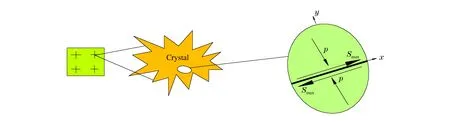
图1 裂纹面热点模型示意图Fig.1 Schematic diagram of hot spot in crack

给定2个交界单元的应力值，就能确定局部应变能的释放率。然后，在模拟程序中的每一时间步长末端，就能确定界面裂纹开裂长度的变化。如果界面的裂纹开裂长度比单元边缘长度宽，界面失效，通过对交界界面节点进行非强制限制而允许界面分离。模拟时，失效的界面合并成宏观裂缝。如果剪切应力超过了某一滑移准则，就设定交界的裂纹面产生滑移。滑移面滑动作功将产生热量，并可能点燃含能材料。这个由摩擦引发的热点模型包含了能量平衡以及裂纹表面随同的力学和化学热源项。一维裂纹表面热传导方程为：

(6)

式中：下标f和s分别代表液态和固态，lf为热点长度尺度，μd为动摩擦因数，k为热导率，cV为定容热容，ρ为密度，ΔH为爆轰热，Z为指前因子，E为活化能，R为普适气体常数。

等式左侧项是热点区的热量；等式右侧第1项是从热点区域由热传导散失的热量，第2项是单位体积化学反应所产生的热量。对于每个有限元，偏应力是在一个平面最大主应变率的法方向，如果最大剪应力值超过了μdp值，则设定裂纹滑动并产生热。对式(6)进行编程，参数来源于自定义Visco-SCRAM材料模型的计算结果。

2 弹体侵彻过程装药温升计算

弹体为尖头弹，如图2所示。混凝土厚度为2.4 m，材料抗压强度为40 MPa，为了考虑侵彻混凝土边界效应，靶体直径为10倍弹体直径。装药为PBX炸药，弹体内壁与装药的摩擦因数为0.12[9]。炮击实验测得弹体着靶速度分别为462、510和651 m/s时，弹体装药均发生点火反应。

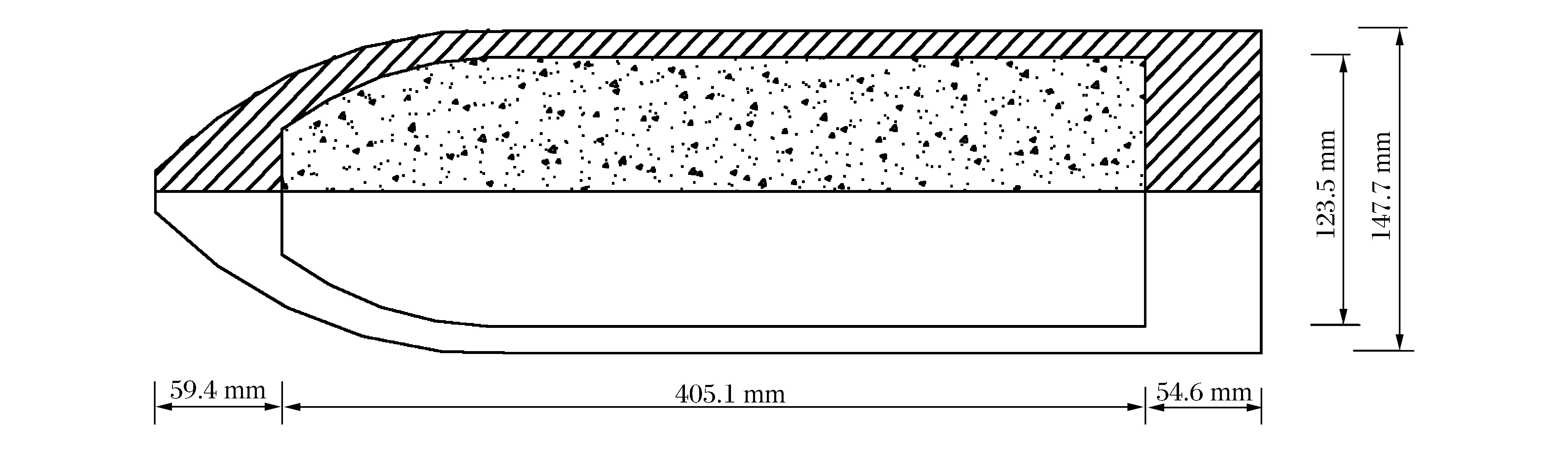
图2 弹体和装药结构示意图Fig.2 Schematic structure of the projectile and charge

图3 弹体侵彻靶体1/4计算模型Fig.3 One-fourth of the calculation model for a projectile penetrating a target

2.1 计算模型

弹体正侵彻靶体的物理模型呈轴对称，建立计算模型时忽略了引信等结构，为减少计算量节省计算时间，建立1/4计算模型，如图3所示。

2.2 材料参数

实验用PBX装药的配方成份与PBX9501炸药相近，采用PBX9501炸药参数进行数值模拟，表1～3中分别给出了PBX9501炸药的黏弹性参数[2-8]、统计裂纹参数[2-8]和热力学参数[2-8]。表2中ν为泊松比，m为裂纹扩展速度指数，c0为裂纹初始半径，vmax为最大的裂纹增长速度，K0为材料断裂韧性。

表1 PBX9501炸药的黏弹性参数[2-8]Table 1 Viscoelasticity parameters of PBX9501[2-8]

表2 PBX9501炸药统计裂纹参数[2-8]Table 2 Crack parameters of explosive PBX9501[2-8]

表3 PBX9501炸药热力学参数[2-8]Table 3 Thermodynamics parameters of explosive PBX9501[2-8]

2.3 计算结果

采用自定义的Visco-SCRAM材料模型计算弹体内壁与装药摩擦温升、装药整体温升以及结合式(6)自编程序计算装药裂纹摩擦生热。下面以弹体侵彻速度分别为440和430 m/s为例，考察3种机制在装药温升方面的贡献。

2.3.1 弹体内壁与装药摩擦温升计算结果

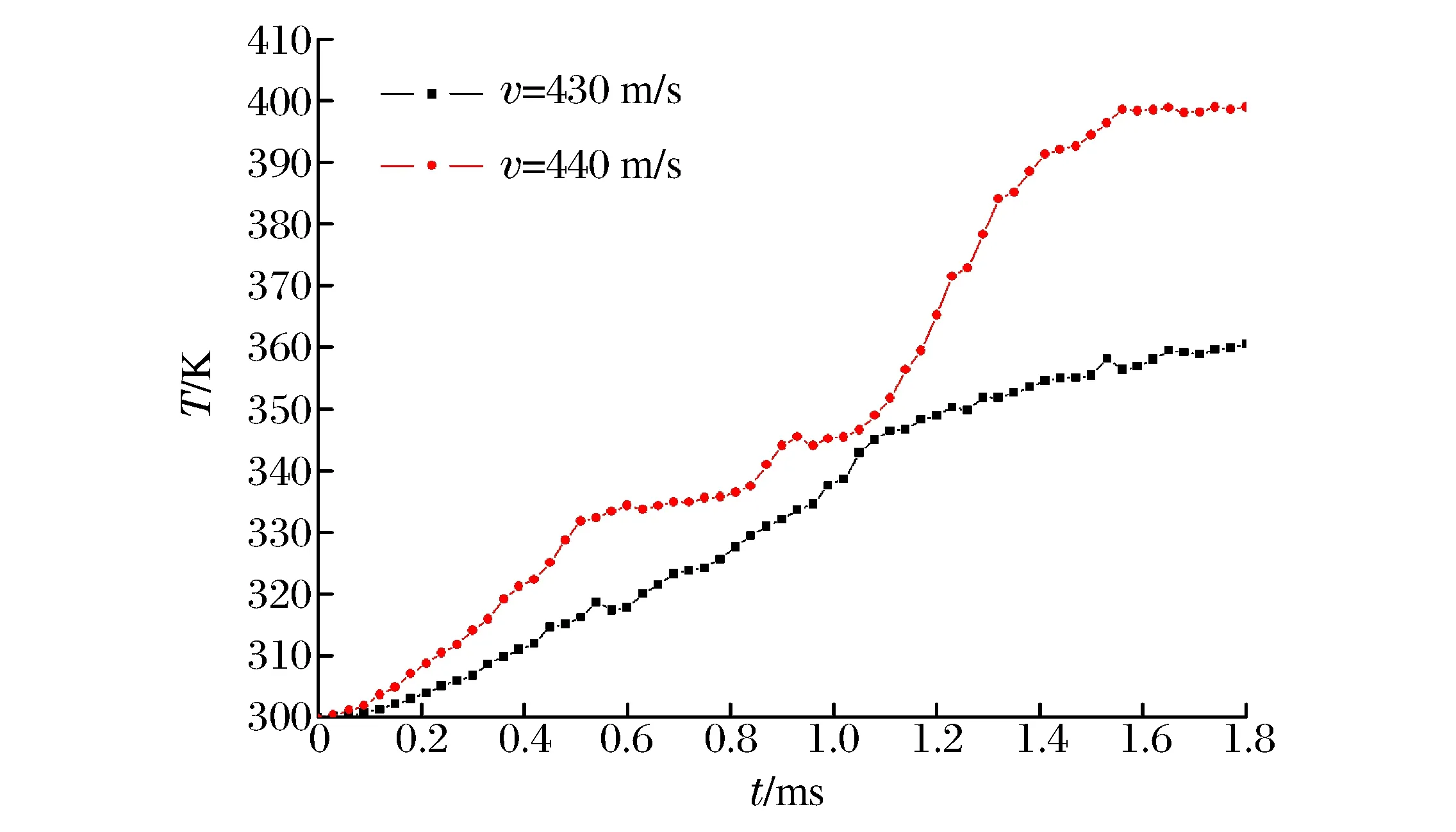
图4 不同初始侵彻速度下装药最高温单元的温度变化曲线Fig.4 Temperature-time curves of the elements with maximum temperature rise in the charge at different initial penetration velocities

对弹体内壁与装药摩擦温升的计算是在Visco-SCRAM模型的基础上考虑弹体内壁与装药之间的摩擦作功生热。图4给出了弹体初始侵彻速度分别为440和430 m/s时最高温升单元的温度变化曲线。从图4可以看出，随着弹体初始侵彻速度的提高，装药与弹体内壁摩擦引起的装药温升也在升高。采用Arrhenius化学动力学方程后，点火温度的判据就是dT/dt→∞。在弹体初始侵彻速度为440 m/s的情况下，侵彻1.65 ms时装药最高温度达到401 K，温升达到101 K，但仍未达到装药的点火温度，1.65 ms时刻之后，装药温度下降，装药最终未发生点火反应。

2.3.2 装药整体温升计算结果

装药整体温升包括黏性、损伤和绝热体积变化导致的温升，还有化学分解热引起的温升。图5给出了在弹体初始侵彻速度为430 m/s的情况下基于整体温升模型得到的装药温度分布云图。

从图5中可以看出，在弹体侵彻早期，装药整体温升主要集中在装药头部，这是由于装药受到压缩而发生变形，绝热压缩功转化为热，即式(3)的第1项在装药温升中所起到的作用。随着弹体逐渐侵入到混凝土内，整个装药都有不同程度的温升。在1 110 μs 时刻，装药最高温度为314 K，温升仅约14 K，远没有达到点火温度。装药的尾部损伤很严重，但温升并不显著，这是由于装药损伤引起的温升没有起到明显作用，即式(3)中的第2项并不是引起温升的主要机制。由于整个装药由力学机制引发的温升不突出，由式(3)第3项，即化学反应放热导致的温升更弱。

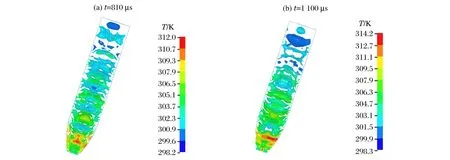
图5 在基于整体温升模型得到的装药温度分布云图Fig.5 Temperature contours of the charge based on the bulk temperature rise model at the initial penetration velocity of 430 m/s

2.3.3 装药裂纹摩擦的热点温升计算结果

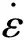
(1)静水压力和最大剪切应变率

沿装药轴向选取6个特征位置上的单元，即单元27120、27286、27394、27473、27915和28225，如图6所示，考察这些单元在弹体侵彻靶板过程中的静水压力及最大剪切应变率，并将这些值在1.0～1.8 ms时域内做平均化处理，进行后续的热点计算。

图6 装药单元位置示意图Fig.6 Schematic diagram of the characteristic explosive elements selected along the axial of the charge

图7给出了弹体初始侵彻速度为440 m/s时装药不同特征单元的静水压力随时间的变化曲线。静水压以压为正，拉为负。装药尾部位置，即单元27120的静水压力最小，装药头部单元28225的静水压力最大。整体上，由装药尾部向头部静水压力逐渐增大。弹体初始侵彻速度为450 m/s时，装药特征单元27120、27286、27394、27473、27915和28225对应的平均静水压力分别为0.6、14、35、62、69和78 MPa；弹体初始侵彻速度为440 m/s时，装药上述特征单元对应的平均静水压力分别为0.44、12、36、64、77和80 MPa；弹体初始侵彻速度为430 m/s时，装药上述特征单元对应的平均静水压力分别为0.3、11、30、45、50和62 MPa。

图8给出了弹体初始侵彻速度为440 m/s时装药不同特征单元的最大剪切应变率随时间的变化曲线。弹体初始侵彻速度为450 m/s时，装药特征单元27120、27286、27394、27473、27915和28225对应的平均最大剪切应变率依次为1.0×103、1.8×103、2.5×103、4.7×103、7.0×103和11.8×103s-1；弹体初始侵彻速度为440 m/s时，上述特征单元对应的平均最大剪切应变率依次为0.92×103、1.5×103、3.8×103、7.3×103、6.1×103和11.0×103s-1；弹体初始侵彻速度为430 m/s时，上述特征单元对应的平均最大剪切应变率依次为0.8×103、1.2×103、1.3×103、2.0×103、2.2×103和2.4×103s-1。

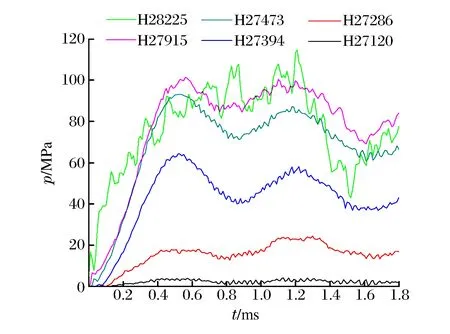
图7 在弹体初始侵彻速度为440 m/s的情况下，装药不同位置处单元的静水压力变化曲线Fig.7 Hydrostatic pressure histories of the explosiveelements at different positions in the chargeat the initial penetration velocity of 440 m/s

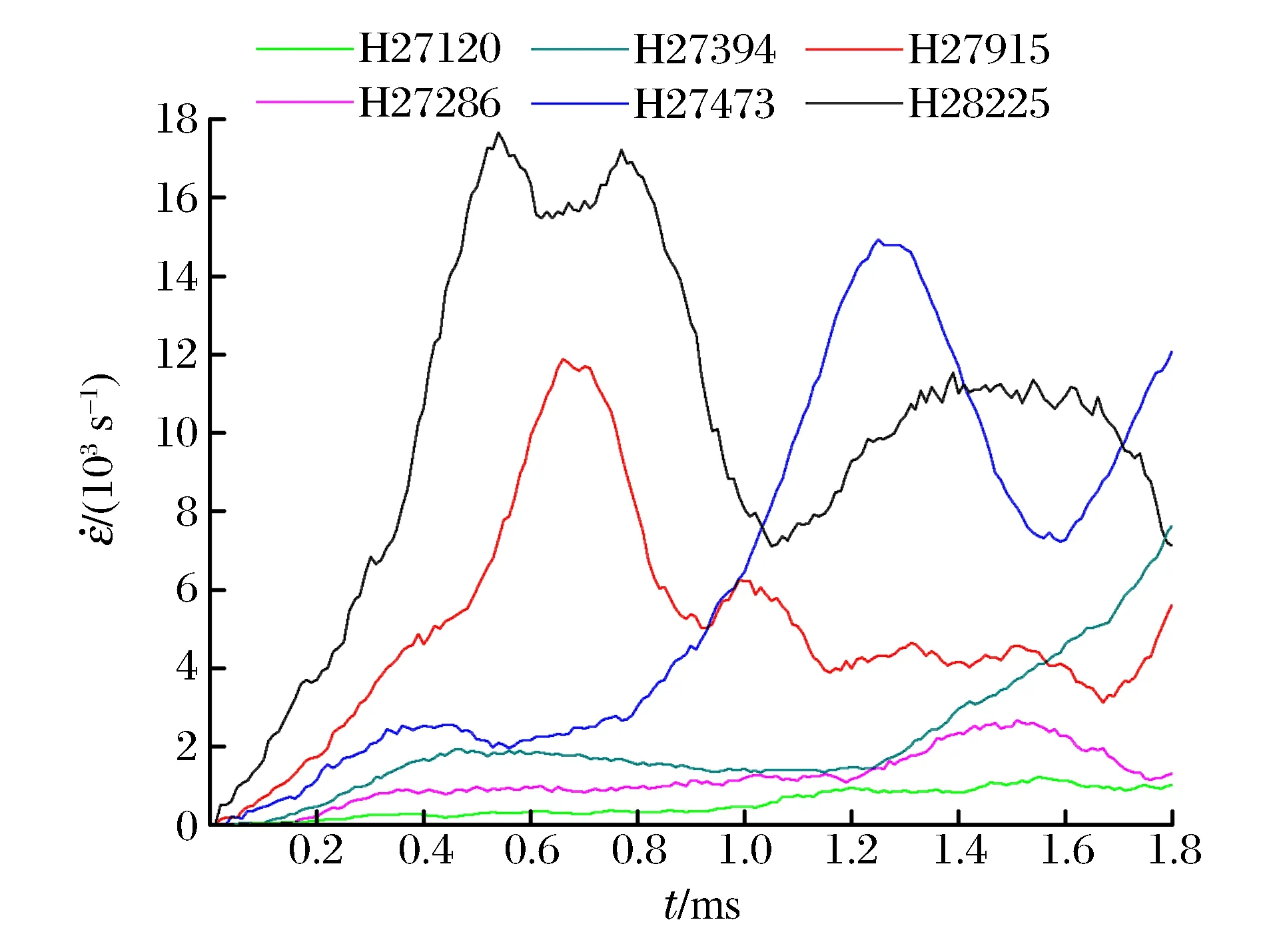
图8 在弹体初始侵彻速度为440 m/s的情况下，装药不同位置处单元的最大剪切应变率变化曲线Fig.8 Maximum shear strain rate histories of the explosive elements at different positions in the chargeat the initial penetration velocity of 440 m/s

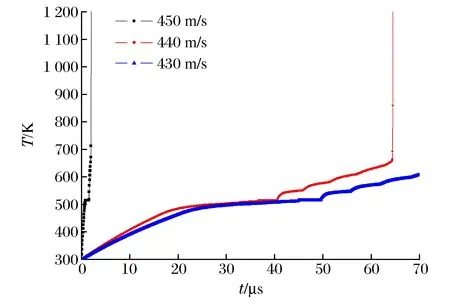
图9 3种不同初始侵彻速度下装药内单元28225热点区域的温度变化曲线Fig.9 Temperature-time curves in the hot spot of explosive element 28225 in the charge at three different initial penetraion velocities

(2)热点温升

通过图7和8中给出的特征单元静水压力和最大剪切应变率，可以计算出各单元的热点温升。图9给出了弹体初始撞击速度为450、440和430 m/s的条件下单元28225热点区域的温升曲线。从图9可以看出，当弹体初始撞击速度为430 m/s时，热点区域的温度仅升至510 K，而弹体初始撞击速度为440和450 m/s时该单元的热点均发生点火反应。

综上分析，弹体装药点火对应的弹体初始侵彻速度在430～440 m/s之间，实验给出的装药发生燃烧反应对应的弹体初始侵彻速度为462 m/s时，尽管数值模拟采用PBX9501炸药代替实验中的炸药，但数值模拟结果有一定的参考意义，验证了Visco-SCRAM模型在计算装药非冲击点火问题的可行性。同时，对比装药与弹体内壁摩擦生热、装药整体温升以及装药裂纹摩擦形成热点3种机制在装药温升方面的作用可以看出，裂纹摩擦形成热点是侵彻装药点火的物理机制。

3 结 论

基于Visco-SCRAM模型,采用热-力耦合算法对弹体侵彻过程中装药的安全性进行了数值模拟，考察了装药与弹体内壁摩擦生热、装药整体温升以及裂纹摩擦形成热点3种机制在装药温升方面的作用,验证了Visco-SCRAM模型用于计算装药非冲击点火问题的可行性，得出如下结论：

(1)装药与弹体内壁摩擦生热对装药温升有一定贡献，随着初始撞击速度的提高，摩擦生热对温升的贡献逐渐增大；

(2)黏性、损伤和绝热体积变化导致的装药整体温升对装药点火的作用有限;

(3)裂纹摩擦形成热点是侵彻装药点火的物理机制；

(4)采用Visco-SCRAM模型可对低强度、长脉冲载荷作用下装药点火响应进行预测。

在本文数值模拟中采用的PBX9501炸药与实验用PBX炸药的物性和力学性能较接近，但并不完全相同。Visco-SCRAM模型中涉及的参数很多，但现有文献中仅给出了PBX9501炸药的裂纹和黏弹性力学参数，下一步需要对其他侵彻装药进行超声波、Hopkinson 杆撞击以及准静态实验，以获取在数值模拟中所需要的Visco-SCRAM模型参数。

[1] Foster J C, Christopher F R, Wilson L L, et al. Mechanical ignition of combustion in condensed phase high explosives[C]∥Shock Compression of Condensed Matter-1997: Proceedings of the Conference of the American Physical Society Topical Group on Shock Compression of Condensed Matter. Amherst, MA, USA: American Institute of Physics, 1997:389-392.

[2] Dienes J K, Kershner J D. Multiple-shock initiation via statistical crack mechanics[C]∥Proceedings of the 11th International Detonation Symposium. Snowmass, CO, USA, 1998:717-724.

[3] Dienes J K, Kershner J D. Crack dynamics and explosive burn via generalized coordinates[J]. Journal of Computer-Aided Materials Design, 2001,7(3):217-237.

[4] Zuo Q H, Dienes J K. On the stability of penny-shaped cracks with friction: The five types of brittle behavior[J]. International Journal of Solids and Structures, 2005,42(5/6):1309-1326.

[5] 赵四海.用粘弹性统计裂纹模型模拟高能炸药的力学响应和非冲击点火[D].长沙:国防科学技术大学,2011:9-12.

[6] Addessio F L, Johnson J N. A constitutive model for the dynamic response of brittle materials[J]. Journal of Applied Physics, 1990,67(7):3275-3286.

[7] Dienes J K. Crack dynamics via Lagrange’s equations and generalized coordinates[J]. Acta Mechanica, 2001,148(1/2/3/4):79-92.

[8] Bennett J G, Haberman K S, Johnson J N, et al. A constitutive model for the nonshock ignition and mechanical response of high explosives[J]. Journal of the Mechanics and Physics of Solids, 1998,46(12):2303-2322.

[9] 陈文.高速侵彻条件下战斗部装药安全性研究[D].北京:北京理工大学,2009:41-42.

[10] Hackett R M, Bennett J G. An implicit finite element material model for energetic particulate composite materials[J]. International Journal for Numerical Methods in Engineering, 2000,49(9):1191-1209.

[11] Dienes J K, Middleditch J, Kershner J D, et al. Progress in statistical crack mechanics: An approach to initiation[C]∥Proceedings of the 12th International Detonation Symposium. Annapolis, USA: Los Alamos National Laboratory, 2002:793-799.

(责任编辑 张凌云)

Investigation on ignition of an explosive charge in a projectile during penetration based on Visco-SCRAM model

Sun Bao-ping, Duan Zhuo-ping1, Wan Jing-lun2, Liu Yan1, Ou Zhuo-cheng1, Huang Feng-lei1

(1.StateKeyLaboratoryofExplosionScienceandTechnology,BeijingInstituteofTechnology,Beijing100081,China；2.ChongqingHongyuPrecisionIndustryCo.Ltd,Chongqing402760,China)

Aimed to the safety of an explosive charge in a projectile during penetration, the visco-statistical crack mechanics (Visco-SCRAM) model was applied to numerically calculate the bulk heat of the explosive charge, the heat produced by the friction between explosive charge cracks, and the heat induced by the friction between the explosive charge and the projectile inner wall. The contribution of the above three mechanisms to the temperature rise of the explosive charge were analyzed, the ignition mechanism of the explosive charge was discussed, and the critical initial penetration velocity of the projectile was obtained corresponding to the ignition of the explosive charge. The investigated results show as follows: (1) the heat induced by the friction between the explosive charge and the projectile inner wall has a certain contribution to the temperature rise of the explosive charge, and this contribution gradually increases as the initial penetration velocity of the projectile increases; (2) the bulk temperature rise produced by the viscosity, damage and adiabatic volume change plays a weak role in the ignition of the explosive charge; (3) the hot spot formation by the friction between the explosive charge cracks is the physical mechanism for the ignition of the explosive charge; (4) the Visco-SCRAM model can be used to predict the ignition responses of explosive charges to low strength and long pulse loads

mechanics of explosion; ignition; visco-statistical crack mechanics model; penetration charge; bulk heat; crack; hot spot

10.11883/1001-1455(2015)05-0689-07

2014-02-21；

2014-05-27

国家自然科学基金项目(11272059)

孙宝平(1976— )，男，博士; 通讯作者： 段卓平,duanzp@bit.edu.cn。

O381 国标学科代码： 13035

A