内部爆炸加载下柱壳的环周分裂数*
2015-04-13张志彪黄风雷
张志彪,黄风雷
(北京理工大学爆炸科学与技术国家重点实验室,北京 100081)
内部爆炸加载下柱壳的环周分裂数*
张志彪,黄风雷
(北京理工大学爆炸科学与技术国家重点实验室,北京 100081)
基于有限长度柱壳的Gurney速度公式,以壳体平均半径估算平均应变率,同时考虑壳体剪切断裂时的断裂面长度与径向壁厚的差异,对Grady-Kipp方法进行了修正,得到柱壳剪切断裂模式下环周分裂数的完整表达式。利用修正方法分析得到的环周分裂数计算结果与实验数据分析结果符合更好。以20号低碳钢柱壳为例,对其在TNT爆炸加载下的膨胀断裂进行了三维数值模拟,得到的环周分裂数模拟结果与实验结果符合较好。
爆炸力学;环周分裂数;爆炸加载;柱壳;动态断裂;低碳钢
为了提高侵彻战斗部的结构强度和抗失稳特性,在战斗部设计中常采用锥型变壁厚弹体结构,通过侵入掩体内部后爆炸,形成破片和爆炸冲击波等毁伤元,实现对目标高效毁伤。因此,在内部爆炸加载下,如何定量描述变壁厚柱壳膨胀破裂产生自然破片的形态及统计分布,是进行毁伤效应评价的基础。关于柱壳沿环向自然破片平均分裂数(即环周分裂数nθ),已经开展了深入的研究。N.F.Mott[1]结合统计物理和应力波理论,系统给出了经典的破片尺寸和统计分布。D.E.Grady等[2-4]将N.F.Mott的统计模型与能量平衡理论结合起来,描述膨胀环的动态破坏和破片数,给出了脆性材料动态破碎的破片尺寸分布。W.Arnold等[5]则采用统计靶板穿孔的方法对柱壳破片分布进行了研究。此外,文献[6]中也有一些相关研究成果,基于实验与量纲分析方法,综合得出了环周分裂数的尺度效应关系。鲁宇等[7]提出了爆炸环动态断裂的修正Kipp-Grady模型;周风华等[8]模拟了韧性金属圆环的自由膨胀碎裂过程,证实了Grady-Kipp公式的合理性;王永刚等[9]在径向膨胀Al2O3陶瓷环动态拉伸破碎方面进行了实验研究,给出了陶瓷环的表观动态拉伸强度。但以上工作主要涉及脆性材料或膨胀环,没有考虑柱壳剪切断裂面长度与径向壁厚的差异。为深入分析韧性材料在内部爆炸加载下的破碎特性,本文中基于有限长度柱壳的Gurney速度公式,采用平均半径估算壳体平均应变率,考虑柱壳剪切断裂的断裂面长度与径向壁厚的差异,拟得到剪切断裂模式下钢柱壳环周分裂数的表达式。同时,基于AUTODYN[10]对爆炸加载下20号钢柱壳的膨胀断裂进行数值模拟,并与实验结果和理论分析结果进行比较。
1 柱壳的环周分裂数
1.1 考虑壁厚的柱壳环周分裂数
D.E.Grady[4]基于N.F.Mott[1]的塑性卸载波理论,将内部爆炸加载下膨胀破坏的柱壳看作刚塑性体。当壳体某处发生断裂后,有2道塑性卸载波分别向两侧传播,传过的壳体区域发生卸载,裂纹停止发展,无法完成断裂。根据达到临界裂纹张开位移时的断裂能,可确定相应的断裂时间,从而得到塑性卸载波传播的距离。该距离的2倍即为壳体周向的平均裂纹间隔,同时也是平均破片宽度:
(1)
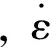
nθ=π(r1+r2)/S
(2)
(3)
假设柱壳以考虑有限长度的Gurney[11]公式得到的破片最终速度向外膨胀,则径向膨胀速度v为:
(4)
式中:G为柱壳装药的Gurney速度,γe为装药密度,L为柱壳长度。由式(1)~(4),可得:
(5)
1.2 破碎能与柱壳断裂模式
金属柱壳在受到内部爆炸加载下膨胀破坏时,主要有2种断裂模式:拉伸断裂和剪切断裂。其中拉伸断裂主要是I型裂纹,材料断裂韧性决定了破碎能Γt,因此有:
(6)
式中:Kc为材料的断裂韧性,E为材料的弹性模量。而对于剪切断裂,主要沿绝热剪切带发生破坏,能量主要耗散于绝热剪切过程,D.E.Grady等给出了如下破碎能[12]:
(7)
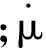
由式(1)~(7)即可得到柱壳剪切断裂模式下环周分裂数的完整表达式。D.E.Grady在应用剪切破碎能Γs时,并没有考虑断裂面取向问题[13],采用一维Gurney公式求得膨胀速度,没有考虑柱壳的有限长度,得到的柱壳环周分裂数简化表达式为[13]:
(8)
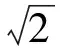
(9)
式(9)中考虑了有限柱壳长度,同时对剪切断裂面长度进行了修正。
1.3 20号钢柱壳算例
以20号低碳钢柱壳为研究对象,假设壳体内装药为TNT,内爆加载下20号钢柱壳的膨胀破坏以贯穿滑移的剪切断裂为主[6],分析该柱壳环周分裂数。计算参数为:G=2 370 m/s,α=0.000 66 K-1,c=500 J/(kg·K),ρ=7 860 kg/m3,γe=1 550 kg/m3,k=52 W/(m·K),Y=0.5 GPa,L=0.16 m。考虑剪切带的热软化,假设热软化系数α有如下关系[12]:τ=Y[1+α(T0-T)]。可知随着温度的升高,剪切带的应力τ逐渐减小,假设达到金属熔化温度Tm时τ减小为0[13]。以内外半径分别为r1=0.02 m和r2=0.03 m,长L=0.16 m的20号钢柱壳为例,可计算得到不考虑剪切断裂面取向时环周分裂数nθ为34,而考虑剪切断裂面取向时nθ为31,nθ降低约10%。通过文献[6]中实验回收破片和高速光学照相方法,计算得到的环周分裂数为28,说明考虑柱壳的有限长度以及剪切断裂面取向时,分析计算结果与实验结果符合更好。引入壳体相对壁厚:δd=δ0/d0,δ0是壳体壁厚,d0是壳体外直径。内半径r1为0.02 m,长L为0.16 m的柱壳在相对壁厚δd=1/12,1/8,1/6,1/5,1/4时, 对应的柱壳环周分裂数理论值分别为42、36、31、28、24,且δd=1/6时对应的柱壳环周分裂数实验值为28。该柱壳在相对壁厚为1/6,长度L=0.02,0.05,0.07,0.11,0.16,0.20,0.50,1.00 m时的环周分裂数理论值分别为24、28、29、30、31、31、32和32。在相对壁厚为1/6时,随着柱壳长度的增加,环周分裂数逐渐趋近于32,长度较短时,环周分裂数明显较小。这是因为柱壳较短时爆轰产物在两端的稀疏效应增强,符合物理实际。
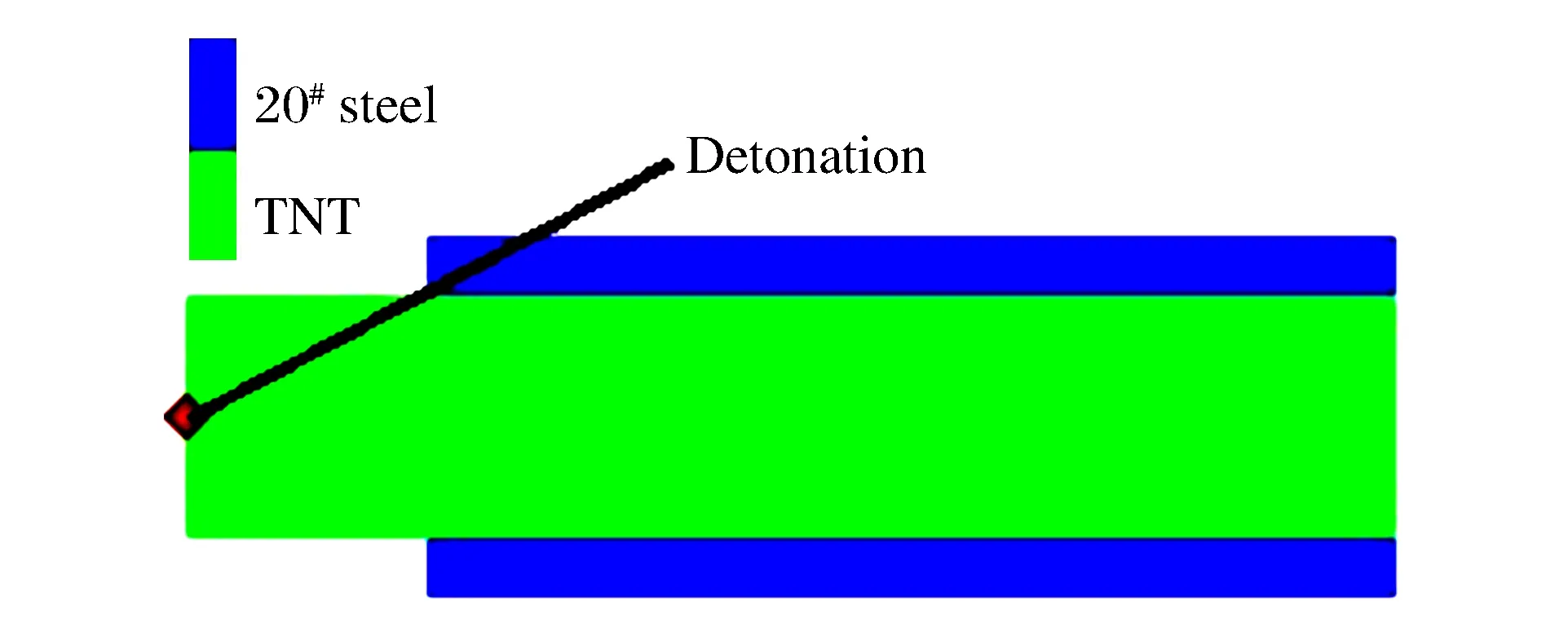
图1 计算模型示意图(工况7)Fig.1 Sketch of calculation model (condition 7)
2 柱壳环周分裂数的三维数值模拟
2.1 计算模型与网格
基于AUTODYN软件,对20号低碳钢柱壳在TNT装药爆炸加载下的膨胀破碎过程进行了三维数值模拟,计算工况见表1,le为装药长度,工况7为实验条件[6],见图1。采用光滑粒子法进行计算,20号钢柱壳及TNT炸药粒子填充的初始间距均取1 mm,工况10的总体粒子数最多,共84.5万。

表1 柱壳环周分裂数的三维数值模拟工况Table 1 3D numerical simulation conditions of circumferential fragments number
2.2 材料模型
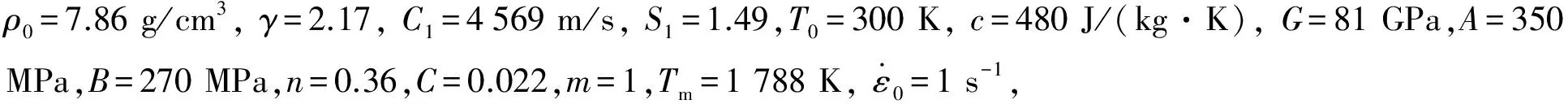
3 数值模拟结果及与讨论
3.1 数值模拟结果
计算得到了20号低碳钢柱壳破裂的图像,如图2所示。SPH方法计算的结果显示,20号钢壳体破片多为长条形,而实验中同样观察到了120~140 mm的长条形破片[6]。由图像可数出典型工况下的柱壳环周分裂数(主要破片),如表2所示。

图2 工况7壳体破裂图像Fig.2 The image for the broken shell of condition 7
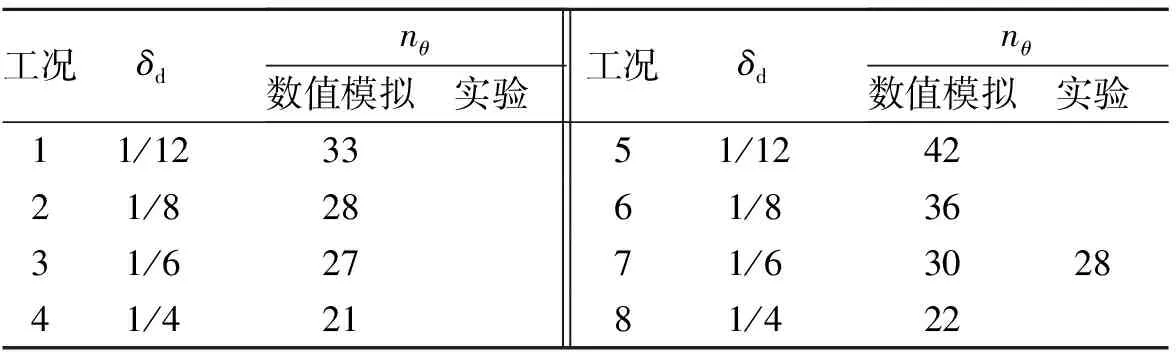
表2 典型工况下柱壳环周分裂数Table 2 Circumferential fragments number of typical conditions
由表2可知,在相同内半径下,装药量不变,随着柱壳壁厚的增加,壳体的环周分裂数逐渐减小,工况7的数值模拟结果与实验结果比较符合。由于所有工况均采用同样的材料参数与同样的SPH粒子初始填充间距,因此各工况的数值模拟结果是可信的。
3.2 理论结果与数值模拟结果的比较
如图3所示,数值模拟结果与相关理论分析结果比较后可知:基于有限长度Gurney公式,并考虑剪切断裂面取向对Grady-Kipp方法进行修正,所得到的环周分裂数nθ比修正前低10%左右;修正后的理论分析结果与数值模拟结果更相符,工况7的数值模拟结果与实验数据点符合较好。
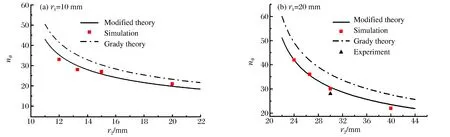
图3 内半径为10,20 mm时环周分裂数与外半径的关系Fig.3 Relationship between the circumferential fragments number and the outer radius when the inner radius is 10, 20 mm
3.3 柱壳环周分裂数的尺度效应
引入量纲一的壳体相对壁厚δd=δ0/d0,长径比λ=r1/L,外半径r2由相对壁厚δd表示,则有:
(10)
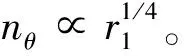
4 结 论
(1)基于有限长度柱壳的Gurney速度公式,以壳体平均半径估算平均应变率,同时考虑壳体剪切断裂时的断裂面长度与径向壁厚的差异,对Grady-Kipp方法进行了修正,得到了柱壳剪切断裂模式下,环周分裂数的完整表达式。利用修正方法分析得到的环周分裂数与实验结果符合更好。(2)以20号低碳钢柱壳为例,对其在TNT内爆加载下的膨胀断裂进行三维数值模拟,得到的环周分裂数数值模拟结果与实验数据点符合较好。修正Grady-Kipp方法的预测结果,与相同参数下各工况的数值模拟结果符合更好,优于未修正的Grady-Kipp方法。(3)采用有限长度柱壳的Gurney速度公式,环周分裂数在柱壳较短时明显较小,这是因为爆轰产物在柱壳两端的稀疏作用增强,符合物理实际。(4)柱壳环周分裂数存在尺度效应,剪切断裂模式下,由修正的Grady-Kipp方法得到的尺度效应关系与实验关系相符。
[1] Mott N F. Fragmentations of shell cases[J]. Proceedings of the Royal Society of London: Series A: Mathematical and Physical Sciences, 1947,189(1018):300-308.
[2] Grady D E, Olsen M L. A statistics and energy based theory of dynamic fragmentation[J]. International Journal of Impact Engineering, 2003,29(1):293-306.
[3] Grady D E. Fragment size distributions from the dynamic fragmentation of brittle solids[J]. International Journal of Impact Engineering, 2008,35(12):1557-1562.
[4] Grady D E. Fragmentation of rings and shells: The legacy of N.F.Mott[M]. Springer, 2006
[5] Arnold W, Rottenkolber E. Fragment mass distribution of metal cased explosive charges[J]. International Journal of Impact Engineering, 2008,35(12):1393-1398.
[6] 奥尔连科.爆炸物理学:下[M].孙承纬,译.北京:科学出版社,2011.
[7] 鲁宇,周兰庭.爆炸环动态破裂分析[J].兵工学报,1991(1):86-90. Lu Yu, Zhou Lan-ting. Dynamic fracture of explosion rings[J]. Acta Armamentarii, 1991(1):86-90.
[8] 陈磊,周风华,汤铁钢.韧性金属圆环高速膨胀碎裂过程的有限元模拟[J].力学学报,2011,43(5):861-870. Chen Lei, Zhou Feng-hua, Tang Tie-gang. Finite element simulations of the high velocity expansion and fragmentation of ductile metallic rings[J]. Acta Mechanica Sinica, 2011,43(5):861-870.
[9] 王永刚,周风华.径向膨胀Al2O3陶瓷环动态拉伸破碎的实验研究[J].固体力学学报,2008,29(3):245-249. Wang Yong-gang, Zhou Feng-hua. Experimental study on the dynamic tensile fragmentations of Al2O3rings under radial expansion[J]. Chinese Journal of Solid Mechanics, 2008,29(3):245-249.
[10] Century Dynamics Inc. Interactive non-linear dynamic analysis software AUTODYN user’s manual[M]. Revision 14.0, 2011.
[11] Lambert D E, Weiderhold J. Explosively driven fragmentation experiments for continuum damage modeling[J]. Journal of Pressure Vessel Technology, 2012,134(3):031209-7.
[12] Grady D E, Kipp M E. The growth of unstable thermoplastic shear with application to steady-wave shock compression in solids[J]. Journal of the Mechanics and Physics of Solids, 1987,35(1):95-119.
[13] Grady D E, Hightower M M. Natural fragmentation of exploding cylinders: DE90016108[R]. Albuquerque, NM: Sandia National Labs, 1990.
[14] 蒋建伟,张谋,门建兵.小口径榴弹自然破片形成过程的数值模拟[J].弹箭与制导学报,2009,29(1):114-117. Jiang Jian-wei, Zhang Mou, Men Jian-bing. Numerical simulation of the formation of natural fragments from a small caliber shell[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2009,29(1):114-117.
[15] Allen S P. Stress-wave monitoring of erosive particle impacts[D]. Australia: The University of Newcastle, 2004.
[16] 宋浦,杨凯,梁安定,等.国内外TNT炸药的JWL状态方程及其能量释放差异分析[J].火炸药学报,2013,36(2):42-45. Song Pu, Yang Kai, Liang An-ding, et al. Difference analysis on JWL-EOS and energy release of different TNT charge[J]. Chinese Journal of Explosives and Propellants, 2013,36(2):42-45.
(责任编辑 张凌云)
本刊关于稿件、版权等的声明
在投稿、稿件处理、发表等过程中,作者需注意如下问题:
1.稿件是作者独立取得的原创性研究成果,无抄袭,无一稿多投,未在国内外公开发表过。
2.稿件无政治错误,不涉及保密和拟申请专利的内容,已经过作者单位保密审查。
3.作者署名和排序无异议,单位署名和排序无争议,且无知识产权纠纷。在稿件处理过程中,如有作者或单位署名变更,需有全体作者亲笔签名和全部单位盖章同意的书面声明。
4.稿件由编辑部组织审稿。自收稿之日时,编辑部将在4个月内反馈处理结果。若超过4个月未答复的,作者有权另行处理稿件,但需事先通知编辑部。
5.对录用的稿件,在尊重稿件内容的基础上,编辑部有权作必要的修改和删减,按规定进行标准化和规范化。
6.稿件录用后,稿件的所有出版权归编辑部。
7.稿件发表后,编辑部赠送样刊,并一次性付给作者稿酬及版权转让费。
爆炸与冲击
2015年9月25日
首届全国爆炸与冲击动力学青年学者学术研讨会
爆炸与冲击动力学是一个交叉性的力学分支学科,主要研究爆炸、冲击和能量突然沉积等强动载荷下介质、材料与结构的力学响应、效应及工程技术应用。当前,爆炸与冲击动力学的发展重点和学科前沿主要有非平衡爆轰与爆轰波结构,复杂介质状态方程的本构理论与材料动态力学,复杂结构高速撞击与侵彻动力学,超高速碰撞新原理和新方法,多场耦合模型建立与多尺度高精度计算方法以及在武器装备、航空航天和民用安全等领域的应用研究等。爆炸与冲击动力学及其相关学科的迅速发展,对研究人员提出了更高要求,及时跟踪国际最新研究进展对青年学者成长非常重要,而发展国际领先的创新方法、解决本领域前沿科学问题,迫切需要在研究队伍方面培育新的增长点。
为了深入交流和探讨爆炸与冲击动力学学科的最新进展和面临的挑战性科学问题,为青年工作者提供深入交流和合作的机会,由国家自然科学基金委员会数理科学部发起和资助,国家自然科学基金委员会数理科学部和中国力学学会爆炸力学专业委员会共同主办的"首届全国爆炸与冲击动力学青年学者学术研讨会"将于2015年10月30日-11月1日在北京举行。会议拟邀请若干国内知名学者介绍相关领域的前沿研究成果和科研经验,同时邀请40名左右爆炸与冲击动力学领域的优秀青年学者进行学术和经验交流。
本次研讨会由北京理工大学爆炸与科学技术国家重点实验室承办,北京理工大学刘彦教授和王成教授负责组织。
国家自然科学基金委员会数理科学部
中国力学学会爆炸力学专业委员会
2015年9月25日
The number of circumferential fragments of a cylindrical shell subjected to internal explosive loading
Zhang Zhi-biao, Huang Feng-lei
(StateKeyLaboratoryofExplosionScienceandTechnology,BeijingInstituteofTechnology,Beijing100081,China)
Based on the Gurney velocity formula for cylindrical shells with finite length, the average strain rate was estimated by the average radius of the shell. And by taking into account the differences between the shear fracture surface length of the shell and the radial thickness, the Grady-Kipp method was modified to give a full expression for the number of the circumferential fragments of the cylindrical shell. The number of the circumferential fragments number calculated by the modified Grady-Kipp method can better match with the experimental result than one by the Grady theory. The 20#low-carbon steel was taken as an example to numerically simulate the expansion and fracture of low-carbon steel shells under TNT explosion loading. The numbers of the circumferential fragments of the low-carbon steel shells by numerical simulation are in agreement with the experimental one.
mechanics of explosion; number of circumferential fragments; explosive loading; cylindrical shell; dynamic fracture; low-carbon steel
10.11883/1001-1455(2015)05-0763-05
2014-01-16;
2014-05-16
张志彪(1986— ),男,博士研究生; 通讯作者: 黄风雷,huangfl@bit.edu.cn。
O383 国标学科代码: 13035
A
