含化学反应膛口流场的无网格数值模拟*

吴 伟,许厚谦,王 亮,薛 锐

(南京理工大学能源与动力工程学院，江苏 南京 210094)



含化学反应膛口流场的无网格数值模拟*

吴 伟,许厚谦,王 亮,薛 锐

(南京理工大学能源与动力工程学院，江苏 南京 210094)

基于无网格方法，对包含大位移运动边界和非平衡化学反应的膛口流场进行了数值模拟。所发展算法是基于线性基函数最小二乘显式无网格方法，忽略黏性及湍流的影响，对流场采用ALE(arbitrary Lagrangian-Eulerian)形式的Euler方程描述，对流通量和化学反应源项采用多组分HLLC(Harten-Lax-van Leer-Contact)格式和有限速率反应模型计算，对于运动边界造成的点云畸形采用局部点云重构方法处理，重构过程中采用虚拟边阵面推进。对圆柱绕流和激波诱导燃烧流场进行了数值模拟，验证了重构方法和化学反应计算的有效性。最后对12.7 mm口径机枪膛口流场进行了模拟，结果同实验照片、非结构网格方法结果吻合较好，数值结果清晰地再现了膛口初始冲击波、膛口冲击波、欠膨胀射流波系结构的动力学发展过程，以及膛口焰的时间、空间分布特征。

爆炸力学；动态点云；无网格方法；膛口流场；非平衡反应流

弹丸从膛口射出后，膛内高温、高压的火药气体因突然被释放而在膛口外急剧膨胀，形成气动结构异常复杂的膛口射流流场；负氧平衡的火药气体还可能与周围的空气发生剧烈的非平衡化学反应，形成膛口焰；此外，流场几何结构也较为复杂并且包含高速运动的弹丸，这些都给膛口流场的数值模拟带来了巨大的挑战。目前，其数值研究大都建立在网格离散的基础上，并且进行了不同程度的简化，如简化弹丸的形状，忽略化学反应、黏性等。

近几十年，由于实际工程问题日益复杂，传统网格方法出现了一些弊端，而新兴的无网格方法得到了计算流体力学领域内大量学者的关注，该方法摆脱了对网格的依赖，采用一系列节点离散求解域，通过构建各节点的点云，采用最小二乘等方法直接求解强形式的控制方程。由于其求解过程只依赖点与点的联系，无需构造网格，因而对于复杂外形具有更强的适应性，流场内部布点也更为方便快捷。此外，相对于传统网格方法，无网格方法最大的优势是易于处理流场中的大位移运动边界，处理过程中均只需更新相应点的点云信息即可，较非结构网格效率更高。正是由于其内在的灵活性、优越性，无网格方法已经得到了大量研究，并取得了一定成果。AUSM+-UP[1-2]、CUSP[3]、HLLC[4]等高精度、高激波分辨率格式成功应用于无网格方法，对包含大位移运动边界问题发展了重叠点云[5]和局部点云重构[4]技术，此外还发展了一些无网格-笛卡尔网格混合网格算法[1,6-7]。近来，采用无网格方法对激波诱导燃烧流场进行模拟的算法[8]也见报道，但对包含大位移运动刚体的非平衡化学反应流场还无法进行有效模拟。

本文中，采用无网格方法求解ALE形式多组分Euler控制方程，用于非平衡化学反应流场的数值模拟，并结合局部点云重构方法处理流场中的大位移运动边界。首先，介绍改进的重构方法的基本思想，以及所采用的无网格方法；随后，对圆柱绕流和激波诱导燃烧流场进行模拟，验证重构方法和化学反应计算的正确性；最后，对12.7 mm口径机枪膛口流场进行模拟。

1 控制方程

对于包含任意位移运动边界的非平衡化学反应流场，忽略黏性及湍流的影响，采用ALE形式的多组分Euler方程描述：

(1)

式中：U为守恒变量，F、G为对流通量，W为化学反应源项，S为轴对称源项。

U、F、G、W具体定义如下：

2 点云重构

对于运动边界造成的点云畸形采用重构的思想处理。首先,将相邻的卫星点以及各卫星点与中心点互联，形成虚拟边；计算动边界附近离散点点云质量，查找质量不满足计算要求的离散点，进而形成点云重构的空腔，避免了复杂的点云相交性判断[4]；空腔内采用虚拟边推进的方法布点，同时生成网格信息(后处理软件需要网格拓扑信息)，同填充布点[4]相比，该过程避免了后续点云Delaunay三角化过程，提高了效率；布点结束后更新空腔边界离散点和新生成离散点的点云，并进行Laplace光顺处理，重新计算其形函数；最后,采用线性插值的方法计算新生成离散点的物理量。

3 数值方法

3.1 空间离散

本文中发展的无网格方法采用线性基函数最小二乘拟合[4,9]直接求解各离散点的空间导数。假设流动基本变量满足如下线性关系：

(2)

以任意点i(假设周围分布6个卫星点)为例，点i及其卫星点均满足式(2)，将中心点与各卫星点进行叠加后可得：

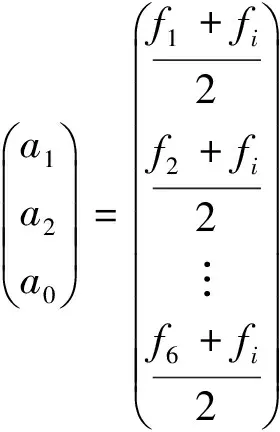
(3)

令上述矛盾方程组的系数矩阵为A，采用最小二乘求解可得：

(4)

进而可得中心点i的空间导数为：

(5)

形函数bij、cij为(ATA)-1AT矩阵的第1、2行，进而中心点i的对流通量则可以表示为：

(6)

对中心点i与其卫星点j的中点的通量Fij采用多组分HLLC格式[9]计算，并采用MUSCL重构方法[1,4]对中点左右两侧状态进行重构，进而提高计算精度。应用于无网格方法的HLLC格式具体形式如下：

(7)

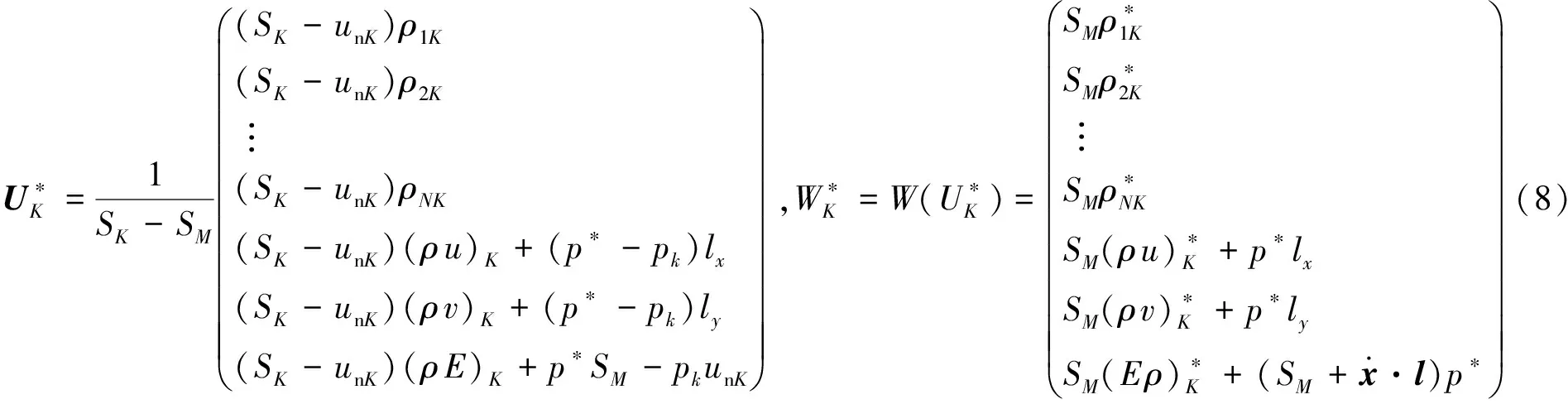
p*=ρi(uni-Si)(uni-SM)+pi

(9)

un为流体速度的法向分量：

(10)

式中：v为流体的速度矢量。

波速Si、Sj以及接触间断面速度SM计算如下：

(11)

(12)

(13)

(14)

3.2 化学反应模型

化学反应源项采用有限速率反应模型，反应体系中的任意反应可表示为：

(15)

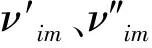
(16)

式中：Am为指前因子，bm为温度因子，Em为活化能，T为混合气体温度，Ru为通用气体常数。逆向反应速率常数Kbm可由反应平衡常数计算。各离散点任意组分i的质量生成率可由下式计算：

(17)

式中：NR为化学反应总数，Mi为组分i的摩尔质量。

3.3 时间项及边界条件

采用四阶Runge-Kutta法进行时间显式推进。边界采用的是在流场外构造镜像点的方法处理，镜像点流动变量的取值则根据边界类型确定。固壁采用法向无穿透边界条件，远场采用基于Riemann不变量的无反射边界条件。

4 验证算例

为验证本文算法正确性，分别对圆柱绕流以及H2/Air预混气体中的激波诱导燃烧流场进行了模拟，并与相关结果进行了比较。

4.1 圆柱绕流流场

为了验证点云重构技术的有效性，对圆柱绕流问题进行了模拟，计算域为2.2 m×1.4 m，圆柱半径为0.1 m，初始时刻位于(0,0)处，计算分2种情形:(1)来流速度v0=0，圆柱运动速度vc=-600 m/s；(2)v0=600 m/s，vc=0。氧气、氮气摩尔比为1∶4，压力p0、温度T0分别为101.325 kPa、286.15 K，计算中冻结化学反应。t=0.8 ms时的压力云图如图1所示，圆柱上表面的量纲一压力p/p0分布如图2所示，可见采用动态点云重构计算得到的结果同圆柱静止时结果吻合较好。

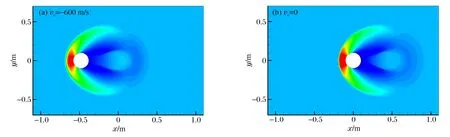
图1 压力云图(t=0.8 ms)Fig.1 Pressure contours at t=0.8 ms

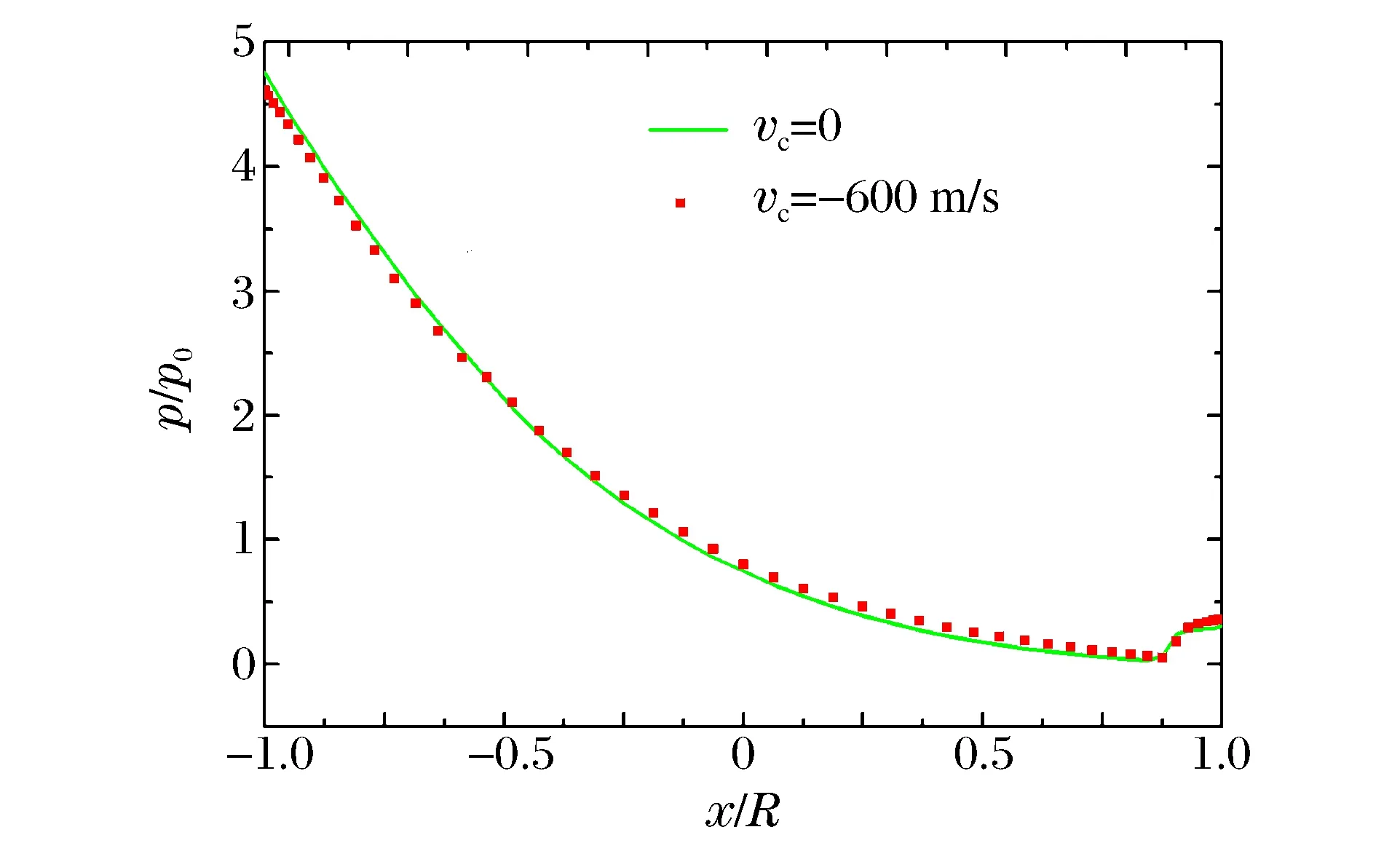
图2 圆柱上表面量纲一压力分布Fig.2 Distribution of the dimensionless pressure along the upper surface of the cylinder

4.2 激波诱导燃烧流场

为验证采用无网格方法计算非平衡化学反应流的有效性，对激波诱导燃烧流场进行了模拟，该算例已经成为验证非平衡化学反应流算法正确性的标准算例。自由来流为等化学当量比的氢气/空气预混气体，来流速度v0、压力p0、温度T0分别为1 685 m/s、42.662 kPa、250 K，化学反应采用7组分8步反应机理[11]。图3为等温线分布图，可见本文算法成功捕捉到了流场中燃烧波与激波的分离，激波位置同实验照片中的结果亦吻合较好。驻点流线上温度、压力以及主要组分质量分数的分布如图4、5所示，同M.Soetrisno等[11]的结果基本一致。

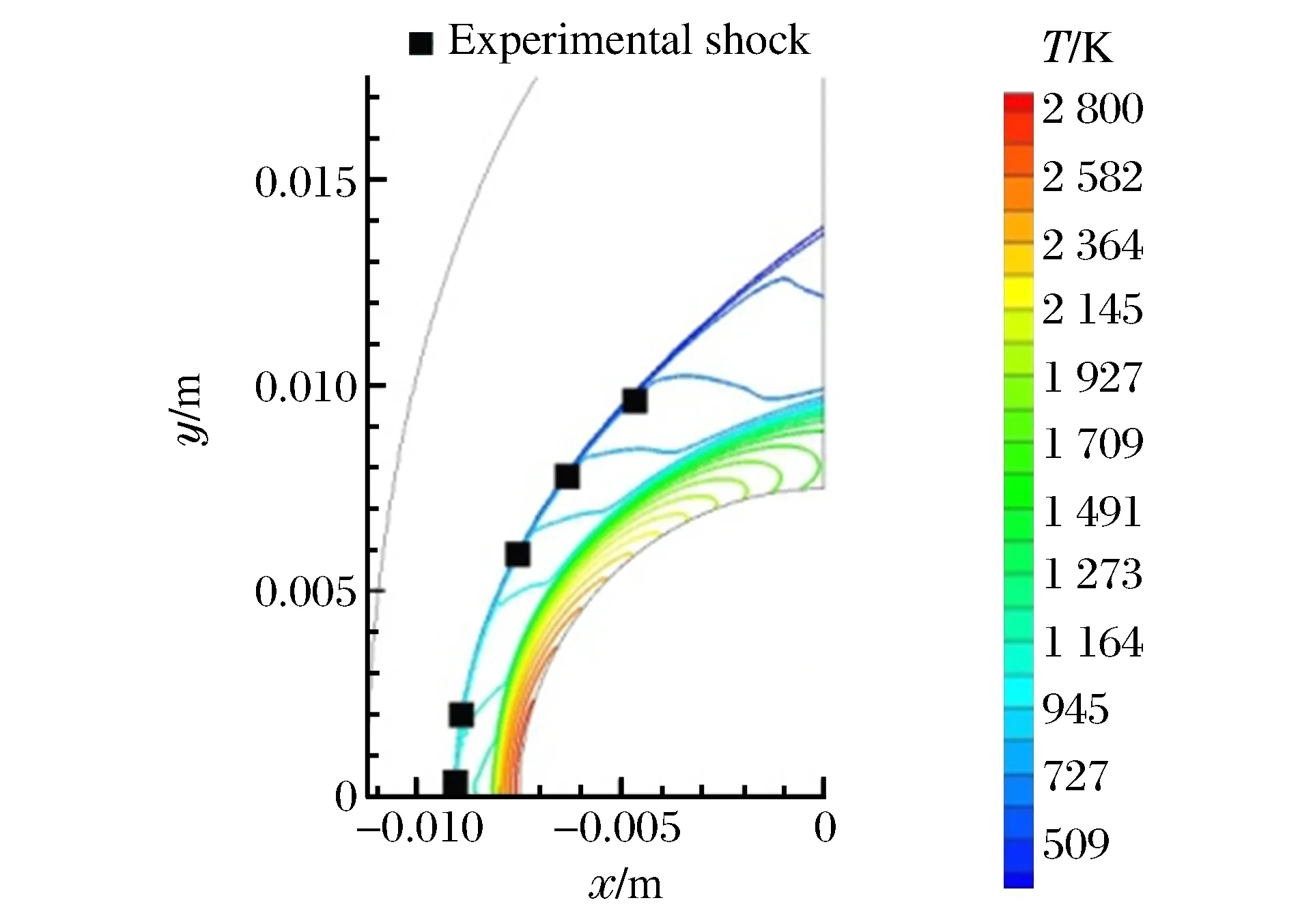
图3 温度云图Fig.3 Temperature contours

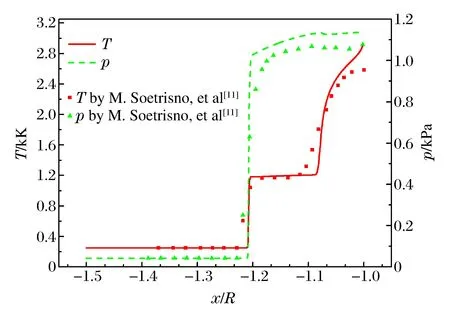
图4 驻点流线上温度、压力分布Fig.4 Distribution of temperature and pressure along the stagnation stream line

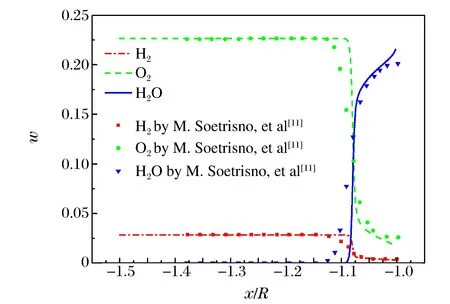
图5 驻点流线上组分质量分数Fig.5 Distribution of mass fractions along the stagnation stream line

图6 膛口离散点分布示意图 Fig.6 Schematic diagram for the distribution of the discrete points at the muzzle

5 膛口二次燃烧流场

对口径为12.7 mm的高射机枪膛口流场进行了数值模拟，膛管的内径为13.7 mm，外径为31.0 mm，膛管长为1.08 m，计算中对弹丸结构进行了适当的简化，其出膛速度为810 m/s。外流场取0.32 m×0.8 m矩形区域，流场共布点228 247个，某时刻流场局部区域离散点分布见图6。定义弹底到达膛口瞬间为0时刻。仅在弹丸出膛后开启化学反应计算，其化学反应采用H2-CO-O29组分11步反应机理[10]。

弹丸在膛内运动部分时刻的温度云图见图7，在火药气体的作用下，弹丸由膛底开始运动，压缩弹前空气，形成一道具有一定强度的激波，弹丸与压缩的空气一同向膛口运动，到达膛口后向周围静止大气环境迅速膨胀，形成包含初始冲击波、马赫盘、瓶状激波、涡环等复杂气动结构的初始射流流场。

当弹丸运动出膛口瞬间(t=0)，需对膛内火药气体组分质量密度、压力、速度等物理量重新赋值，具体如下：

px=pd[1+φ(1-x2/L2)]

vx=v0x/L

(18)

式中：px、vx为膛管内压力和速度，x为距膛底距离，pd为弹丸运动至膛口时弹底压力，取值74 MPa，φ取值0.18。火药气体平均密度ρ0为120 kg/m3，各组分的摩尔分数分别为：CO，0.434 69；CO2，0.099 43；H2，0.135 81；H2O，0.222 63；N2，0.107 44。对温度、总能根据热力学关系计算获得。

图8为不同时刻计算阴影图与实验阴影照片的对比，可见t=0时刻初始冲击波、t=250 μs时刻膛口冲击波、马赫盘的位置、形状等同实验结果吻合较好。图9为采用本文算法计算得到的t=415 μs时刻密度、温度云图同非结构网格方法[10]得到结果的对比。由于本文忽略了后效期火药气体对弹丸的加速作用，假设其以恒定速度运动，因此弹丸位置均有所滞后。

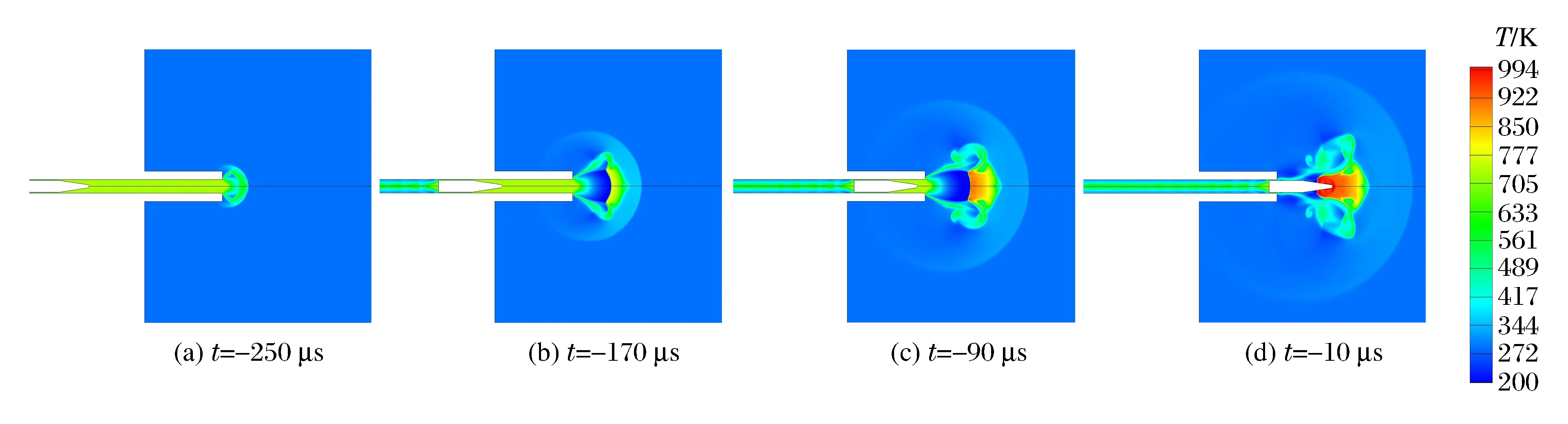
图7 弹丸出膛前不同时刻流场温度分布Fig.7 Temperature contours in the flow field at different times begore the bullet leaves the muzzle

图8 计算阴影图与实验阴影照片比较Fig.8 Computational shadowgraph compared with experimental shadowgraph

图9 t=415 μs时刻的密度、压力云图Fig.9 Density and pressure contours at t=415 μs

弹丸出膛后，负氧平衡的火药气体迅速射入初始流场，与环境中的氧气接触，在一定的温度、压力条件下可能发生化学反应，甚至是剧烈燃烧。本文采用温度T以及OH的质量分数w(OH)分布表征化学反应剧烈程度，弹丸出膛后不同时刻分布云图如图10所示，可见算法成功捕捉到初始冲击波、膛口冲击波、入射斜激波、马赫盘、弹底激波等复杂波系，清晰地展现了激波的传播规律以及膛口焰的发展过程。图11为弹丸与膛口间轴线温度分布曲线。

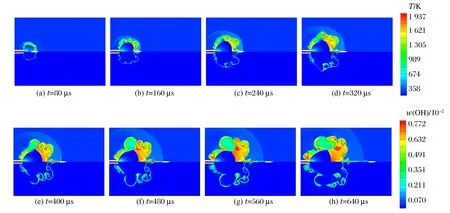
图10 不同时刻温度(上)和OH质量分数(下)分布云图Fig.10 Temperature contours (top) and mass fraction contours f OH (bottom) at different times

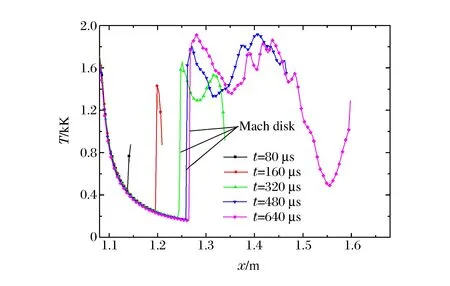
图11 温度沿轴线的分布曲线Fig.11 Temperature distribution along the axis

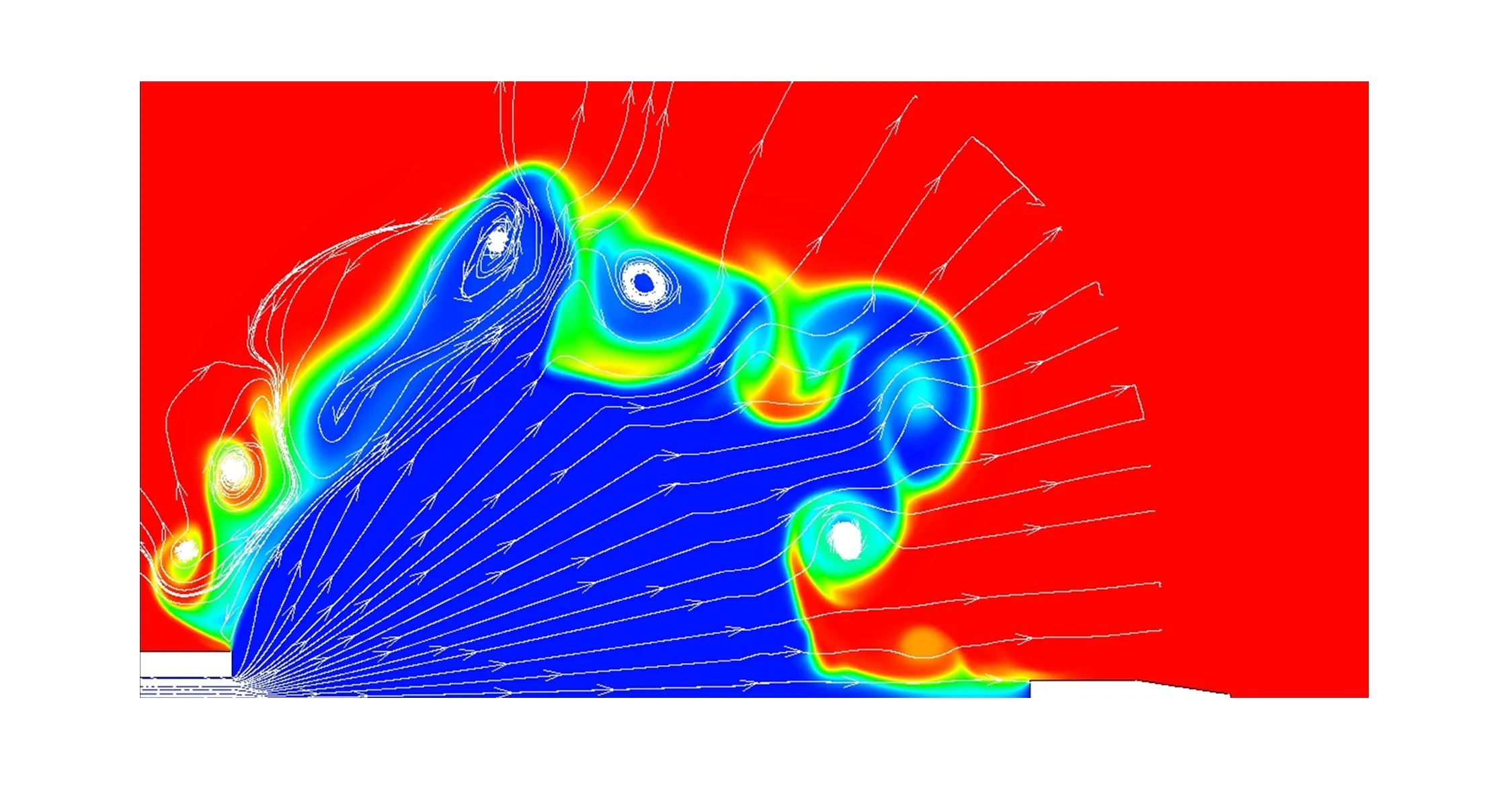
图12 t=400 μs时刻N2质量分数分布及流线Fig.12 N2 mass fraction contours and streamlines at t=400 μs

随着弹丸运动，膛内高温高压火药气体进入初始流场而急剧膨胀，其速度达到2 km/s，迅速超越和包围弹丸，形成相交激波和弹底激波，并且与空气接触面形成相对光滑的初始火焰阵面，如图10(a)所示。由于初始流场的引导作用，加速了火药气体的轴向运动，使得膛口冲击波呈冠状，并迅速赶超初始冲击波。由于边界失稳，氧气被卷入，火焰阵面开始扭曲，如图10(b)所示。图10(c)中包含相交激波、马赫盘在内的完整欠膨胀射流结构形成，并且膛口冲击波基本湮没初始流场。随后弹丸穿越膛口冲击波的过程中,如图10(d)～10(e)所示，马赫盘的生长不再受其影响，射流自由膨胀。t=320 μs时刻，由于自由膨胀，温度大幅下降的火药气体经过马赫盘的再压缩，温度显著上升，达到1 600 K,如图11所示，但是由于马赫盘下游区域缺乏氧气，因此该区域并无剧烈化学反应，但是由于高温火药气体辐射出可见光，可形成中间焰。三波点附近出现向上游回旋的主涡环，将氧气卷入射流边界内，并发生剧烈化学反应，温度达1 900 K，形成二次焰，此外可见OH质量分数分布并不均匀，而是呈卷曲的线状，说明火药气体与环境的质量交换仍不充分，化学反应仍局限在有限的接触面上。当弹丸穿越膛口冲击波后，对膛口流场影响进一步削弱，流场中高温区域显著增多，峰值达2 000 K以上，如图10(f)～10(h)所示。此外受弹丸尾流的影响，部分马赫盘后低速的火药气体被带入下游，与环境中氧气接触，发生化学反应。

N2在本文所采用的化学反应机理中为惰性气体，因此其质量分数分布可一定程度反应火药气体与空气质量交换的强弱，t=400 μs时刻N2质量分数分布及流线如图12所示，可见由于边界不稳定性形成了多个涡环，在其的作用下，射流边界以及马赫盘下游区域部分空气被卷吸进入火药气体内部，除三波点附近的主涡环外，马赫盘下游、射流边界上游存在着一系列小的涡环，这些涡环不断生长、破碎，这些都使得原本清晰、简单的接触面卷曲，进而使火焰阵面变得更复杂。

6 结 论

改进了局部点云重构方法，保证了点云均匀性，提高了计算效率，并建立了可用于包含大位移运动边界，非平衡化学反应流场数值模拟的无网格算法。通过对圆柱绕流以及激波诱导燃烧流场的计算验证了算法的正确性。最后对12.7 mm高射机枪膛口二次燃烧流场进行了数值模拟，其结果清晰地展现了弹丸射出过程中，膛口初始流场、火药气体射流流场同高速运动弹丸的强烈耦合与相互作用；完整地再现了膛口流场复杂波系结构变化的动力学过程以及二次焰分布的时空特征。

本文算法为包含任意位移动边界化学反应流的数值研究提供了有效的工具。

[1] Cai Xiao-wei, Tan Jun-jie, Ma Xin-jian, et al. Application of hybrid Cartesian grid and gridless approach to moving boundary flow problems[J]. International Journal for Numerical Method in Fluid, 2013,72(9):994-1013.

[2] 盛鸣剑,叶正寅,蒋超奇.附面层修正应用于无网格算法的研究[J].计算力学学报,2011,28(6):920-925. Sheng Ming-jian, Ye Zheng-yin, Jiang Chao-qi. Study of boundary layer solution coupled with gridless method[J]. Chinese Journal of Computational Mechanics, 2011,28(6):920-925.

[3] Hashemi M Y, Jahangirian A. An efficient implicit mesh-less method for compressible flow calculations[J]. International Journal for Numerical Methods in Fluids, 2011,67(6):754-770.

[4] 周星.含动边界复杂非定常流动的无网格算法研究[D].南京:南京理工大学,2012.

[5] 马新建.最下二乘无网格及其重叠点云法在CFD中的应用研究[D].南京:南京理工大学,2012.

[6] Kirshman D J, Liu F. A gridless boundary condition method for the solution of the Euler equations on embedded Cartesian meshes with multigrid[J]. Journal of Computational Physics, 2004,201(1):119-147.

[7] Luo H, Baum J D, Löhner R. A hybrid Cartesian grid and gridless method for compressible flows[J]. Journal of Computational Physics, 2006,214(2):618-632.

[8] 吴伟,许厚谦.激波诱导燃烧流场模拟的无网格算法[J].力学与实践,2013,35(6):19-23. Wu Wei, Xu Hou-qian. Meshless method for numerical simulation of shock-induced combustion[J]. Mechanics in Engineering, 2013,35(6):19-23.

[9] Katz A, Jameson A. A comparison of various meshless schemes within a unified algorithm[R]. AIAA Paper, 2009-596,2009.

[10] 代淑兰.复杂化学反应流并行数值模拟[D].南京:南京理工大学,2008.

[11] Soetrisno M, Imlay S T. Simulation of the flow field of a ram accelerator[R]. AIAA Paper, 1991-1915,1991.

(责任编辑 张凌云)

Numerical simulation of a muzzle flow field involving chemical reactions based on gridless method

Wu Wei, Xu Hou-qian, Wang Liang, Xue Rui

(SchoolofPowerEngineering,NanjingUniversityofScienceandTechnology,Nanjing210094,Jiangsu,China)

A gridless method for simulation of reactive flows involving moving boundaries was investigated based on the linear basis least-squares gridless method. The Euler equations of arbitrary Lagrangian-Eulerian form were employed as governing equations. The numerical flux and chemical sources were calculated by the multi-component HLLC ((Harten-Lax-van Leer-Contact) scheme and finite rate reaction model, respectively. An elevated restructuring technique of local cloud was adopted to deal with the moving boundaries. The front advance method of fictitious boundaries was used during the restructuring. The flow around the cylinder and the shock-induced combustion flow field were simulated to validate the accuracy firstly. The muzzle flow of a 12.7 mm machine gun was simulated. The computational shadowgraphs agree well with the experimental photographs, the density and pressure contours are in agreement with the results by the unstructured mesh method. The numerical results show the coupling and interaction progress in the initial muzzle flow field, the under-expanding jet of explosive gas and high-speed projectile clearly, and the temporal, spatial distribution characteristics of the muzzle flash are reappeared plainly.

mechanics of explosion; dynamic cloud; gridless method; muzzle flow field; chemical non-equilibrium flow

10.11883/1001-1455(2015)05-0625-08

2014-02-19；

2014-06-27

吴 伟(1990— )，男，博士研究生,wuwei.njust.804@gmail.com。

O381 国标学科代码： 13035

A