爆破振动速度预测安全保证系数的确定*

梁书锋,王宇涛,2,刘殿书,李 奎,李明慧

(1.中国矿业大学(北京)力学与建筑工程学院,北京 100083;2.保利民爆哈密有限公司,新疆 哈密 839200)



爆破振动速度预测安全保证系数的确定*

梁书锋1,王宇涛1,2,刘殿书1,李 奎1,李明慧1

(1.中国矿业大学(北京)力学与建筑工程学院,北京 100083;2.保利民爆哈密有限公司,新疆 哈密 839200)

基于爆破振动速度预测公式回归分析的基本原理，提出根据建筑物不同安全等级应选择一定的可靠性指标，并推导了预测爆破振动速度公式中所含安全保证系数的计算过程。为简化计算过程，又进一步提出了基于监测数据量、回归分析相关系数以及可靠性指标的关于安全保证系数计算的经验公式。经过大量监测数据验证了该经验公式的计算精度和可靠性均能满足工程实际需要，从而修正了萨氏公式预测精确度不够的缺陷，可为重要建筑物周边的安全爆破设计提供参考。

爆炸力学；安全保证系数；回归分析；爆破振动速度；可靠性指标

对于爆破振动速度的计算，现普遍采用经验公式进行回归分析预测，而中国现主要采用萨道夫斯基公式[1]：

(1)

式中：v为岩石爆破振动速度,Q为装药质量,R为爆破中心到测点的距离,K为与岩石特征、爆破条件有关的系数,α为与场地有关的指数。

采用公式(1)计算爆破振动速度时，K值和α值往往因地质地形条件的不同产生较大差异。同时在利用回归分析得到爆破振速预测公式的过程中，根据数理统计的知识可知，采用这种方法得到的振动速度公式仅有50%的可靠性[2]。这对爆破现场周围重要(构)建筑物将带来较大的安全隐患。为了保证爆破现场周围重要(构)建筑物的安全，在最新修订的《爆破安全规程》(GB6722-2011)中[3-4]，给出了根据建筑物的不同等级以及不同的振动频率得到的安全振动速度范围，并提出了对于重点保护古建筑和古迹的安全允许质点振速，但缺乏定量的分析理论。

本文中，基于回归分析的基本原理，提出了根据建筑物安全等级应选择一定的可靠性指标；计算得到了爆破振动速度安全保证系数，分析了其计算原理；通过大量数据分析提出了安全保证系数的经验计算公式，极大地简化计算过程，可为重要建筑物周边的安全爆破设计提供参考。

1 安全保证系数的计算原理

在回归分析的过程中，通常会把萨道夫斯基公式进行变形，使其转化为一元线性回归分析[5]。将公式(1)两边取对数后转化为：

lnv=lnK+αln (Q1/3/R)

(2)

此时令y=lnv,x=ln (Q1/3/R),b=lnK,则公式(2)即可变形为一元线性方程的形式：

y=αx+b

(3)

通过回归分析得到的y值是预测值，该值与爆破现场的实测振动速度往往会有一定误差。若Y是y在此处的实际值，则可知其与预测结果有关系式：Y=y+ε=b+αx+ε。

虽然误差ε可正可负，其值无法准确计算，但由回归分析的基本原理可知其服从一定的分布[6]：

(4)

由于σ2未知，因而只能用样本数据确定其无偏估计量：

(5)

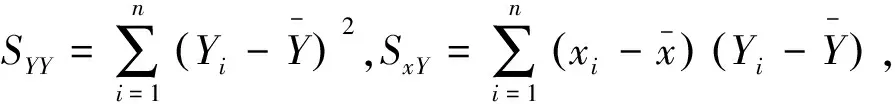
则由数理统计知识可知其分布情况：

(6)

于是对于一定的置信区间1-β(可靠性指标)有：

(7)

考虑置信区间的置信上限水平,取：

(8)

将公式(8)重新代入萨氏公式的形式后为：

(9)

令：

γs=eε

(10)

γs即为萨氏公式中的安全保证系数。

2 影响安全保证系数的因素分析

2.1 样本数据量

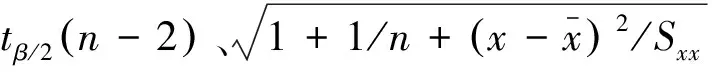
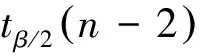
从以上数值可以看出：随着数据量的增大，t函数的值在1-β=99%和1-β=95%等2种情况下均会逐渐减小，表明通过增加爆破振动监测数据量可以适当减小爆破振动安全系数；同时可以发现随着数据量的增加，t函数的值减小幅度逐渐降低并将最终收敛于某一值。由此可知，单纯地依靠增大爆破振动监测数据量，不能有效地减小安全保证系数。

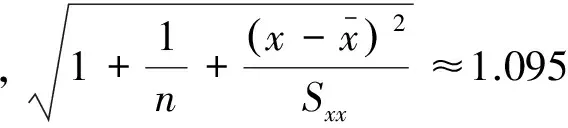
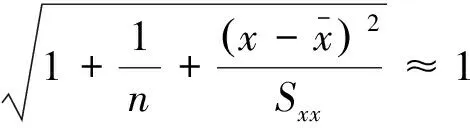
2.2 方差分析

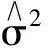
(11)

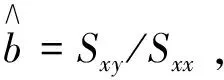
由回归分析基本原理已可知：

(12)

由残差平方和服从的分布状况为Qe/σ2～χ2(n-2)，于是有E(Qe/σ2)=n-2，即知E(Qe/(n-2))=σ2，这样就得到了σ2的无偏估计量：

(13)

3 安全保证系数的经验计算公式

一般在用萨道夫斯基公式进行回归分析预测时，都会给出相关系数以及预测数据量[8]。如果能够根据监测数据量及回归分析的相关系数直接计算安全保证系数，将为工程爆破振动速度的计算和预测提供便利，下面将根据相关系数的计算公式对安全保证系数进行变形计算。相关系数的计算公式为：

(14)

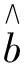
(15)

此时式中仍然存在未知变量Syy，但是经过大量的数据计算后发现Syy/(n-2)的值始终在1/4附近，因而将做如下变换：

(16)

(17)

从式中可以看出，对于一般的爆破振动速度预测结果，只需要知道其预测过程中采用的监测数据量n及其回归结果的r，即可得到γs，极大地简化了计算过程。对于式(17)的精确程度，以工程实例数据为基础与在可靠性回归分析中式(8)～(10)的计算结果进行对比，以此验证。

4 工程实例验算

对安全系数经验公式验证时,采用青岛某码头建设过程中采石场至油库方向的28组监测数据，见表1，表1中qmax为单段最大药量，vh,t为水平横向振动速度，vh,l为水平纵向振动速度，vv为垂直向振动速度。运用式(2)和(3)分别对上述28组监测数据进行空间3个方向的回归分析,见图1～3。

由回归方程(3)通过变换得到K=eA以及α=B，并分别采用经验公式(17)及回归分析基本原理计算得到安全保证系数，其结果整理如表2所示,表中γs,r为采用回归分析法得到的安全系数，γs,e为采用经验公式法得到的安全系数。

由计算结果可看出，采用经验公式得到的安全保证系数与采用回归分析基本原理得到的结果很接近，误差为5%～10%，且采用经验公式的计算结果稍大[9]。这表明采用经验公式得到的计算结果仍然满足安全保证要求，对于重要构建筑物的安全爆破设计更具可靠性。同时仅根据回归分析得到的K、α以及相关系数r就能够直接计算得到安全保证系数，计算方法简便易行，为实际工程计算带来了便利。

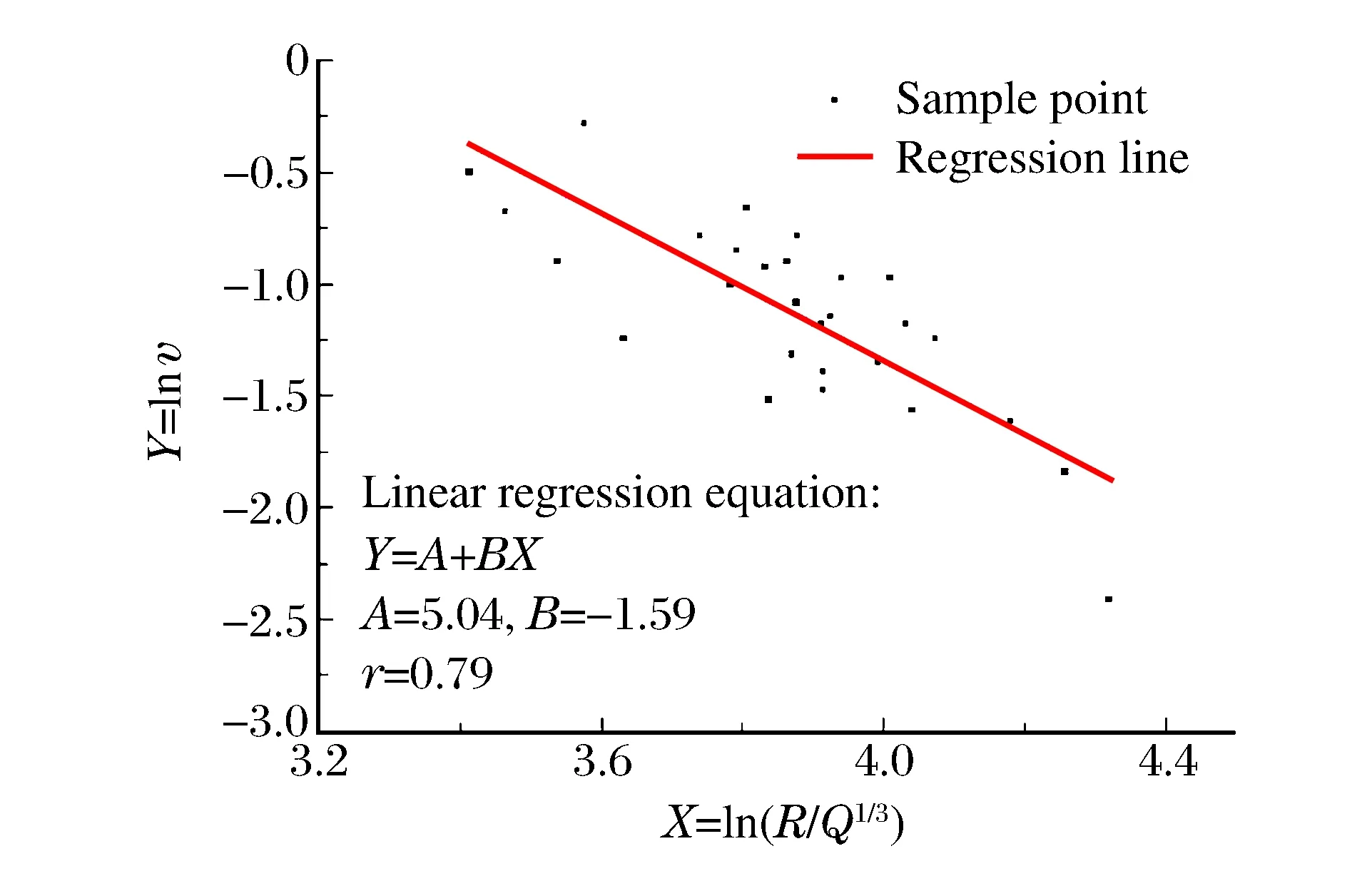
图2 水平纵向回归分析结果Fig.2 Longitudinal regression analysis results

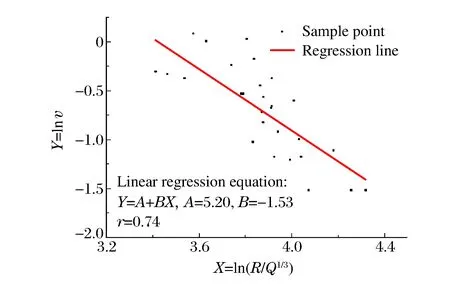
图3 垂直向回归分析结果Fig.3 Vertical regression analysis results

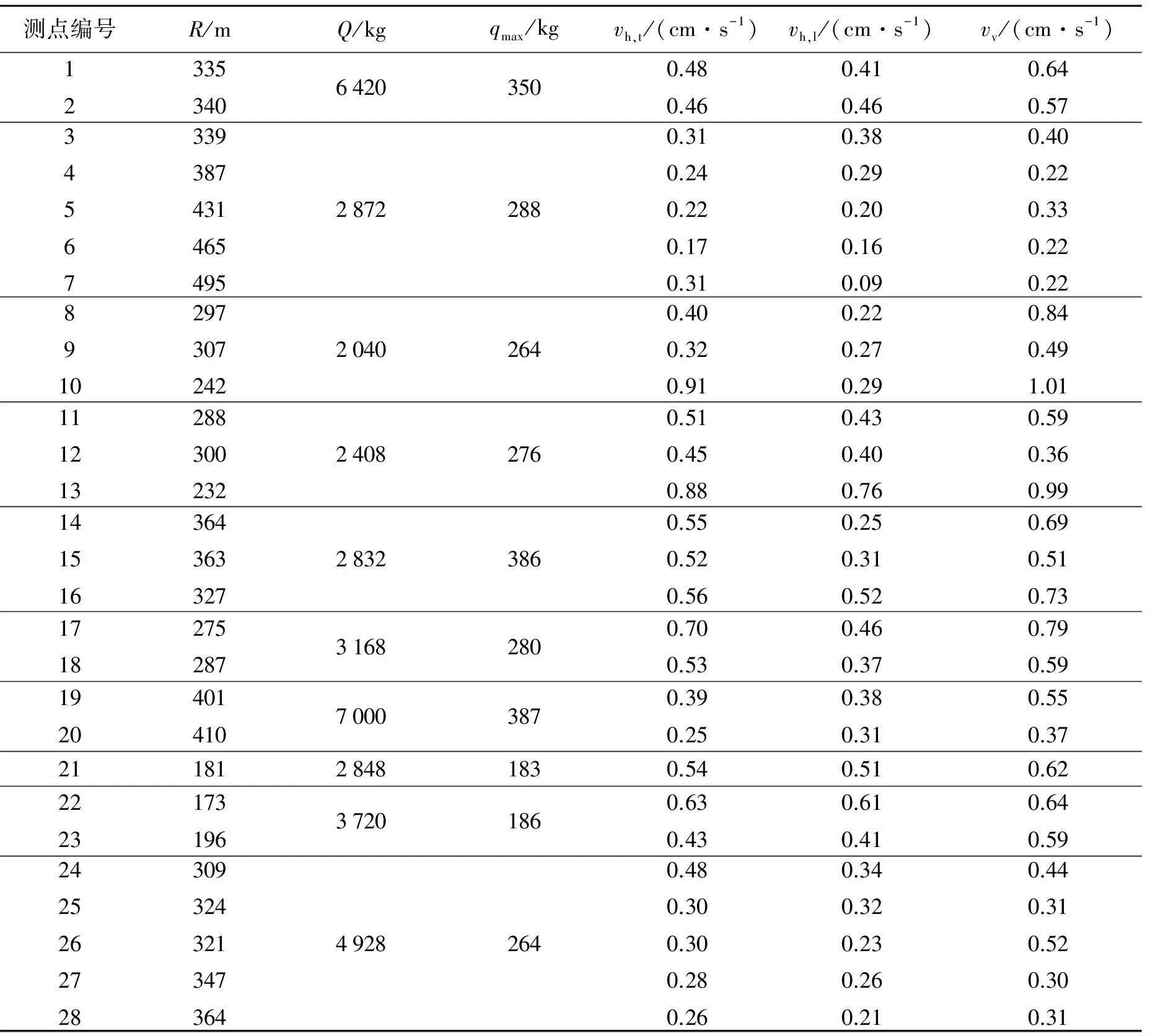
表1 油库方向监测数据Table 1 Data monitored along the direction from the quarry to the oil depot

表2 计算结果Table 2 Calculation results

5 结 语

爆破振动波的传播和衰减规律是进行工程爆破参数设计的重要依据，但是由于爆破现场复杂的地质和地形条件，仅利用萨氏公式往往不能保证振动速度的预测精度。本文通过对某爆破工程的现场数据分析研究，提出根据建筑物的重要程度选择不同的可靠性指标，计算得到安全系数以保证工程周围重要建筑物的安全，同时提出了基于监测数据量、回归分析相关系数以及可靠性指标的计算公式，极大的简化了爆破振动安全保证系数的计算过程，同时根据实际工程监测数据验证了爆破振动安全保证系数计算公式的可行性，为爆破振动速度准确预测提供了可靠的保证。

[1] 刘殿书.爆破工程[M].北京:科学出版社,2011:98-133.

[2] 吕涛,石永强,黄诚,等.非线性回归分析法求解爆破震动速度衰减公式参数[J].岩土力学,2007,28(9):1871-1878. Lü Tao, Shi Yong-qiang, Huang Cheng, et al. Study on attenuation parameters of blasting vibration by nonlinear regression analysis[J]. Rock and Soil Mechanics, 2007,28(9):1871-1878.

[3] 言志信,王永和,江平,等.爆破地震测试及建筑结构安全标准研究[J].岩石力学与工程学报.2003,22(11):1907-1911. Yan Zhi-xin, Wang Yong-he，Jiang Ping, et al. Study on measurement of blast-induced seism and building safety criteria[J]. Journal of Rock Mechanics and Engineering, 2003,22(11):1907-1911.

[4] 中国工程爆破协会.GB6722-2011,爆破安全规程[S].北京:中国标准出版社,2011.

[5] 杨佑发,崔波.爆破震动速度峰值预测[J].振与冲击,2009,28(10):195-198. Yang You-fa, Cui Bo. Prediction for vibration intensity due to blasting induced ground motions[J]. Journal of Vibration and Shock, 2009,28(10):195-198.

[6] 盛骤.概率论与数理统计[M].北京:高等教育出版社,2008:40-60.

[7] Kim D S, Lee J S . Propagation and attenuation characteristics of various ground vibrations[J]. Soil Dynamics and Earthquake Engineering, 2000,19(2):115-126.

[8] 杜汉清.爆破振动衰减规律的现场试验研究[J].爆破,2007,24(3):107-109. Du Han-qing. Experimentally study on the attenuation law of blasting vibration[J]. Blasting, 2007,24(3):107-109.

[9] 毕卫国,石崇.爆破振动速度衰减公式的优化选择[J].岩土力学,2004,25(增刊):99-102. Bi Wei-guo, Shi Chong. Optimization selection of blasting vibration velocity attenuation formulas[J]. Rock and Soil Mechanics, 2004,25(Suppl):99-102.

(责任编辑 张凌云)

Determination of safety coefficient for predicting blasting vibration velocity

Liang Shu-feng1, Wang Yu-tao1，2, Liu Dian-shu1, Li Kui1, Li Ming-hui1

(1.SchoolofMechanicsandCivilEngineering,ChinaUniversityofMiningandTechnology(Beijing),Beijing100083,China；2.PolyExplosivesHamiCo.,Ltd,Hami839200,Xinjiang,China)

The basic principle of regression analysis was considered for the prediction formula of blasting vibration velocity. On the basis of the considered principle, an opinion was put forward that certain reliability indexes should be chosen according to the safety levels of buildings. And the calculation process was deduced for the safety assurance coefficient included in the prediction formula of blasting vibration velocity. To simplify the calculation process, an empirical calculation formula was proposed for the safety assurance coefficient based on the parameters consisting of amount of monitoring data, correlation coefficient of regression analysis, and reliability index. The accuracy and reliability of the empirical calculation formula was verified by the monitoring data in actual projects. The investigated results show that the empirical calculation formula can meet the practical needs and it can make up the shortcoming that the accuracy of Sadov’s formula is not enough. So the empirical calculation formula proposed can provide a reference for the design of safety blasting surrounding important buildings.

mechanics of explosion; safety assurance coefficient; regression analysis; blasting vibration velocity; reliability index

10.11883/1001-1455(2015)05-0741-06

2014-03-28；

2014-06-26

教育部博士点基金项目(20100023110001)

梁书锋(1982— )，男，博士研究生; 通讯作者： 王宇涛,w_yt2052@163.com。

O382；TD235 国标学科代码： 13035

A